9.4: Panua Mizizi ya Mraba

Last updated

Nov 1, 2022
Page ID
177358
Save as PDF
- 9.3E: Mazoezi
- 9.4E: Mazoezi

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Kuzidisha mizizi ya mraba
Tumia kuzidisha kwa polynomial kuzidisha mizizi ya mraba

Kumbuka

Kabla ya kuanza, fanya jaribio hili la utayari.

Kurahisisha: (3u) (8v).
Kama amekosa tatizo hili, mapitio Mfano 6.2.31.
Kurahisisha: 6 (12-7n).
Ikiwa umekosa tatizo hili, tathmini Mfano 6.3.1.
Kurahisisha: (2+a) (4,1a).
Kama amekosa tatizo hili, mapitio Mfano 6.3.34.

Kuzidisha mizizi ya Mraba

Tumetumia Mali ya Bidhaa ya Mizizi ya Mraba ili kurahisisha mizizi ya mraba kwa kuondoa mambo kamili ya mraba. Mali ya Bidhaa ya Mizizi ya Square anasema

$\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber$

Tunaweza kutumia Mali ya Bidhaa ya Mizizi ya Mraba 'katika reverse' kuzidisha mizizi ya mraba.

$\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber$

Kumbuka, sisi kudhani vigezo vyote ni kubwa kuliko au sawa na sifuri.

Tutaandika tena Mali ya Bidhaa ya Mizizi ya Mraba ili tuone njia zote mbili pamoja.

Ufafanuzi: PRODUCT PROPERTY YA MIZIZI

Ikiwa a, b ni nambari halisi zisizo na hasi, basi

$\sqrt{ab}=\sqrt{a}·\sqrt{b}$ na $\sqrt{a}·\sqrt{b}=\sqrt{ab}$ .

Hivyo tunaweza kuzidisha $\sqrt{3}·\sqrt{5}$ in this way:

$\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}$

Wakati mwingine bidhaa hutupa mraba kamili:

$\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}$

Hata wakati bidhaa si mraba kamili, ni lazima kuangalia kwa sababu kamilifu mraba na kurahisisha radical wakati wowote iwezekanavyo.

Kuzidisha radicals na coefficients ni sawa na kuzidisha vigezo na coefficients. Kuzidisha 4x·3y sisi kuzidisha coefficients pamoja na kisha vigezo. Matokeo ni 12xy. Kuweka hii katika akili kama wewe kufanya mifano hii.

Mfano $\PageIndex{1}$

Kurahisisha:

$\sqrt{2}·\sqrt{6}$
$(4\sqrt{3})(2\sqrt{12})$ .

Jibu

1.	$\sqrt{2}·\sqrt{6}$
Kuzidisha kutumia Mali ya Bidhaa.	$\sqrt{12}$
Kurahisisha radical.	$\sqrt{4}·\sqrt{3}$
Kurahisisha.	$2\sqrt{3}$
2.	$(4\sqrt{3})(2\sqrt{12})$
Kuzidisha kutumia Mali ya Bidhaa.	$8\sqrt{36}$
Kurahisisha radical.	$8·6$
Kurahisisha.	$48$

Mfano $\PageIndex{2}$

Kurahisisha:

$\sqrt{3}·\sqrt{6}$
$(2\sqrt{6})(3\sqrt{12})$ .

Jibu

$3\sqrt{2}$
$36\sqrt{2}$

Mfano $\PageIndex{3}$

Kurahisisha:

$\sqrt{5}·\sqrt{10}$
$(6\sqrt{3})(5\sqrt{6})$

Jibu

$5\sqrt{2}$
$90\sqrt{2}$

Mfano $\PageIndex{4}$

Kurahisisha: $(6\sqrt{2})(3\sqrt{10})$

Jibu

	$(6\sqrt{2})(3\sqrt{10})$
Kuzidisha kutumia Mali ya Bidhaa.	$18\sqrt{20}$
Kurahisisha radical.	$18\sqrt{4}·\sqrt{5}$
Kurahisisha.	$18·2·\sqrt{5}$
	$36\sqrt{5}$

Mfano $\PageIndex{5}$

Kurahisisha: $(3\sqrt{2})(2\sqrt{30})$

Jibu: $12\sqrt{15}$

Mfano $\PageIndex{6}$

Kurahisisha: $(3\sqrt{3})(3\sqrt{6})$ .

Jibu: $27\sqrt{2}$

Tunapopaswa kuzidisha mizizi ya mraba, tunapata kwanza bidhaa na kisha tuondoe mambo yoyote ya mraba kamili.

Mfano $\PageIndex{7}$

Kurahisisha:

$(\sqrt{8x^3})(\sqrt{3x})$
$(\sqrt{20y^2})(\sqrt{5y^3})$

Jibu

1.	$(\sqrt{8x^3})(\sqrt{3x})$
Kuzidisha kutumia Mali ya Bidhaa.	$\sqrt{24x^4}$
Kurahisisha radical.	$\sqrt{4x^4}·\sqrt{6}$
Kurahisisha.	$2x^2\sqrt{6}$
2.	$(\sqrt{20y^2})(\sqrt{5y^3})$
Kuzidisha kutumia Mali ya Bidhaa.	$\sqrt{100y^5}$
Kurahisisha radical.	$10y^2\sqrt{y}$

Mfano $\PageIndex{8}$

Kurahisisha:

$(\sqrt{6x^3})(\sqrt{3x})$
$(\sqrt{2y^3})(\sqrt{50y^2})$ .

Jibu

$3x^2\sqrt{2}$
$10y^2\sqrt{y}$

Mfano $\PageIndex{9}$

Kurahisisha:

$(\sqrt{6x^5})(\sqrt{2x})$
$(\sqrt{12y^2})(\sqrt{3y^5})$

Jibu

$2x^3\sqrt{3}$
$6y^2\sqrt{y}$

Mfano $\PageIndex{10}$

Kurahisisha: $(10\sqrt{6p^3})(3\sqrt{18p})$

Jibu

	$(10\sqrt{6p^3})(3\sqrt{18p})$
Kuzidisha.	$30\sqrt{108p^4}$
Kurahisisha radical.	$30\sqrt{36p^4}·\sqrt{3}$
	$30·6p^2·\sqrt{3}$
	$180p^2\sqrt{3}$

Mfano $\PageIndex{11}$

Kurahisisha: $(\sqrt{62x^2})(8\sqrt{45x^4})$

Jibu: $144x^3\sqrt{10}$

Mfano $\PageIndex{12}$

Kurahisisha: $(2\sqrt{6y^4})(12\sqrt{30y})$ .

Jibu: $144y^2\sqrt{5y}$

Mfano $\PageIndex{13}$

Kurahisisha:

$(\sqrt{2})^2$
$(−\sqrt{11})^2$ .

Jibu

1.	$(\sqrt{2})^2$
Andika upya kama bidhaa.	$(\sqrt{2})(\sqrt{2})$
Kuzidisha.	$\sqrt{4}$
Kurahisisha.	2
2.	$(−\sqrt{11})^2$
Andika upya kama bidhaa.	$(−\sqrt{11})(−\sqrt{11})$
Kuzidisha.	$\sqrt{121}$
Kurahisisha.	11

Mfano $\PageIndex{14}$

Kurahisisha:

$(\sqrt{12})^2$
$(−\sqrt{15})^2$ .

Jibu

Mfano $\PageIndex{15}$

Kurahisisha:

$(\sqrt{16})^2$
$(−\sqrt{20})^2$ .

Jibu

Matokeo ya mfano uliopita yanatuongoza kwenye mali hii.

Ufafanuzi: SQUARING ROOT SQUARE

Ikiwa ni nambari halisi isiyo ya kawaida, basi

$(\sqrt{a})^2=a$

Kwa kutambua kwamba mraba na kuchukua mizizi ya mraba ni shughuli 'kinyume', tunaweza kurahisisha $(\sqrt{2})^2$ na kupata 2 mara moja. Tunapozidisha mbili kama mizizi ya mraba katika sehemu (a) ya mfano unaofuata, ni sawa na mraba.

Mfano $\PageIndex{16}$

Kurahisisha:

$(2\sqrt{3})(8\sqrt{3})$
$(3\sqrt{6})^2$ .

Jibu

1.	$(2\sqrt{3})(8\sqrt{3})$
Kuzidisha. Kumbuka, $(\sqrt{3}^2)$	16·3
Kurahisisha.	48
2.	$(3\sqrt{6})^2$
Kuzidisha.	9·6
Kurahisisha.	54

Mfano $\PageIndex{17}$

Kurahisisha:

$(6\sqrt{11})(5\sqrt{11})$
$(5\sqrt{8})^2$ .

Jibu

Mfano $\PageIndex{18}$

Kurahisisha:

$(3\sqrt{7})(10\sqrt{7})$
$(−4\sqrt{6})^2$ .

Jibu

Tumia Uzidishaji wa Polynomial ili Kuzidisha Mizizi

Katika mifano michache ijayo, tutatumia Mali ya Usambazaji ili kuzidisha maneno na mizizi ya mraba.

Sisi kwanza kusambaza na kisha kurahisisha mizizi ya mraba iwezekanavyo.

Mfano $\PageIndex{19}$

Kurahisisha:

$3(5−\sqrt{2})$
$\sqrt{2}(4−\sqrt{10})$ .

Jibu

1.	$3(5−\sqrt{2})$
Kusambaza.	$15−3\sqrt{2})$
2.	$\sqrt{2}(4−\sqrt{10})$
Kusambaza.	$4\sqrt{2}−\sqrt{20}$
Kurahisisha.	$4\sqrt{2}−2\sqrt{5}$

Mfano $\PageIndex{20}$

Kurahisisha:

$2(3−\sqrt{5})$
$\sqrt{3}(2−\sqrt{18})$ .

Jibu

$6−2\sqrt{5}$
$2\sqrt{3}−3\sqrt{6}$

Mfano $\PageIndex{21}$

Kurahisisha:

$6(2+\sqrt{6})$
$\sqrt{7}(1+\sqrt{14})$ .

Jibu

$12+\sqrt{6}$
$\sqrt{7}+7\sqrt{2}$

Mfano $\PageIndex{22}$

Kurahisisha:

$\sqrt{5}(7+2\sqrt{5})$
$\sqrt{6}(\sqrt{2}+\sqrt{18})$ .

Jibu

1.	$\sqrt{5}(7+2\sqrt{5})$
Kusambaza.	$7\sqrt{5}+2·5$
Kurahisisha.	$7\sqrt{5}+10$
	$10+7\sqrt{5}$
2.	$\sqrt{6}(\sqrt{2}+\sqrt{18})$
Kuzidisha.	$\sqrt{12}+\sqrt{108}$
Kurahisisha.	$(\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})$
	$2\sqrt{3}+6\sqrt{3}$
Kuchanganya kama radicals.	$8\sqrt{3}$

Mfano $\PageIndex{23}$

Kurahisisha:

$\sqrt{6}(1+3\sqrt{6})$
$\sqrt{12}(\sqrt{3}+\sqrt{24})$

Jibu

$18+\sqrt{6}$
$6+12\sqrt{2}$

Mfano $\PageIndex{24}$

Kurahisisha:

$\sqrt{8}(2−5\sqrt{8})$
$\sqrt{14}(\sqrt{2}+\sqrt{42})$

Jibu

$−40+4\sqrt{2}$
$2\sqrt{7}+14\sqrt{3}$

Tulipofanya kazi na polynomials, tuliongeza binomials na binomials. Kumbuka, hii ilitupa bidhaa nne kabla ya kuunganisha maneno kama hayo. Ili uhakikishe kupata bidhaa zote nne, tuliandaa kazi yetu—kwa kawaida kwa njia ya FOIL.

Mfano $\PageIndex{25}$

Kurahisisha: $(2+\sqrt{3})(4−\sqrt{3})$

Jibu

	$(2+\sqrt{3})(4−\sqrt{3})$
Kuzidisha.	$8−2\sqrt{3}+4\sqrt{3}−3$
Kuchanganya kama maneno.	$5+2\sqrt{3}$

Mfano $\PageIndex{26}$

Kurahisisha: $(1+\sqrt{6})(3−\sqrt{6})$ .

Jibu: $−3+2\sqrt{6}$

Mfano $\PageIndex{27}$

Kurahisisha: $(4−\sqrt{10})(2+\sqrt{10})$ .

Jibu: $−2+2\sqrt{10}$

Mfano $\PageIndex{28}$

Kurahisisha: $(3−2\sqrt{7})(4−2\sqrt{7})$ .

Jibu

	$(3−2\sqrt{7})(4−2\sqrt{7})$
Kuzidisha.	$12−6\sqrt{7}−8\sqrt{7}+4·7$
Kurahisisha.	$12−6\sqrt{7}−8\sqrt{7}+28$
Kuchanganya kama maneno.	$40−14\sqrt{7}$

Mfano $\PageIndex{29}$

Kurahisisha: $(6−3\sqrt{7})(3+4\sqrt{7})$ .

Jibu: $−66+15\sqrt{7}$

Mfano $\PageIndex{30}$

Kurahisisha: $(2−3\sqrt{11})(4−\sqrt{11})$

Jibu: $41+14\sqrt{11}$

Mfano $\PageIndex{31}$

Kurahisisha: $(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})$ .

Jibu

	$3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})$
Kuzidisha.	$3·2+12\sqrt{10}−\sqrt{10}−4·5$
Kurahisisha.	$6+12\sqrt{10}−\sqrt{10}−20$
Kuchanganya kama maneno.	$−14+11\sqrt{10}$

Mfano $\PageIndex{32}$

Kurahisisha: $(5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})$

Jibu: $1+9\sqrt{21}$

Mfano $\PageIndex{33}$

Kurahisisha: $(\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})$

Jibu: $−12−20\sqrt{3}$

Mfano $\PageIndex{34}$

Kurahisisha: $(4−2\sqrt{x})(1+3\sqrt{x})$ .

Jibu

	$(4−2\sqrt{x})(1+3\sqrt{x})$ .
Kuzidisha.	$4+12\sqrt{x}−2\sqrt{x}−6x$
Kuchanganya kama maneno.	$4+10\sqrt{x}−6x$

Mfano $\PageIndex{35}$

Kurahisisha: $(6−5\sqrt{m})(2+3\sqrt{m})$ .

Jibu: $12+8\sqrt{m}−15m$

Mfano $\PageIndex{36}$

Kurahisisha: $(10+3\sqrt{n})(1−5\sqrt{n})$

Jibu: $10−47\sqrt{n}−15n$

Kumbuka kuwa baadhi ya bidhaa maalum alifanya kazi yetu rahisi wakati sisi kuzidisha binomials mapema. Hii ni kweli wakati sisi kuzidisha mizizi ya mraba, pia. Fomu maalum za bidhaa tulizotumia zinaonyeshwa hapa chini.

Ufafanuzi: FORMULA PRODUCT MAALUM

$\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}$

Tutatumia fomu maalum za bidhaa katika mifano michache ijayo. Tutaanza na formula ya Mraba ya Binomial.

Mfano $\PageIndex{37}$

Kurahisisha:

$(2+\sqrt{3})^2$
$(4−2\sqrt{5})^2$ .

Jibu

Hakikisha kuingiza muda wa 2ab wakati unapokwisha binomial.

	$.$
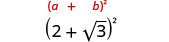
Panua kutumia muundo wa mraba wa binomial.	$.$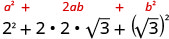
Kurahisisha.	$.$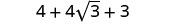
Kuchanganya kama maneno.	$.$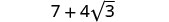

	$.$
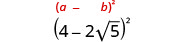
Panua kutumia muundo wa mraba wa binomial.	$.$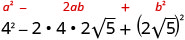
Kurahisisha.	$.$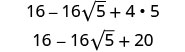
Kuchanganya kama maneno.	$.$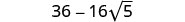

Mfano $\PageIndex{38}$

Kurahisisha:

$(10+\sqrt{2})^2$
$(1+3\sqrt{6})^2$ .

Jibu

$102+20\sqrt{2}$
$55+6\sqrt{6}$

Zoezi $\PageIndex{39}$

Kurahisisha:

$(6-\sqrt{5})^2$
$(9-2\sqrt{10})^2$ .

Jibu

$41-12\sqrt{5}$
$121-36\sqrt{10}$

Mfano $\PageIndex{40}$

Kurahisisha: $(1+3\sqrt{x})^2$ .

Jibu

	$.$
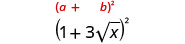
Panua kutumia muundo wa mraba wa binomial.	$.$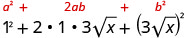
Kurahisisha.	$.$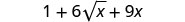

Mfano $\PageIndex{41}$

Kurahisisha: $(2+5\sqrt{m})^2$ .

Jibu: $4+20\sqrt{m}+25m$

Mfano $\PageIndex{42}$

Kurahisisha: $(3−4\sqrt{n})^2$ .

Jibu: $9−24\sqrt{n}+16n$

Katika mifano miwili ijayo, tutapata bidhaa za conjugates.

Mfano $\PageIndex{43}$

Kurahisisha: $(4−\sqrt{2})(4+\sqrt{2})$ .

Jibu

	$.$
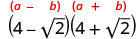
Panua kutumia muundo wa mraba wa binomial.	$.$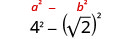
Kurahisisha.	$.$

Mfano $\PageIndex{44}$

Kurahisisha: $(2−\sqrt{3})(2+\sqrt{3})$

Jibu: 1

Mfano $\PageIndex{45}$

Kurahisisha: $(1+\sqrt{5})(1−\sqrt{5})$

Jibu: —4

Mfano $\PageIndex{46}$

Kurahisisha: $(5−2\sqrt{3})(5+2\sqrt{3})$

Jibu

	$.$
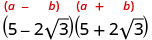
Panua kutumia muundo wa mraba wa binomial.	$.$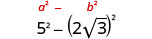
Kurahisisha.	$.$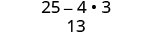

Mfano $\PageIndex{47}$

Kurahisisha: $(3−2\sqrt{5})(3+2\sqrt{5})$ .

Jibu: -11

Mfano $\PageIndex{48}$

Kurahisisha: $(4+5\sqrt{7})(4−5\sqrt{7})$ .

Jibu: -159

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kuzidisha mizizi ya mraba.

Bidhaa Mali
Panua Binomials na Mizizi ya Mraba

Dhana muhimu

Bidhaa Mali ya Mizizi Square Kama, b ni nonnegative namba halisi, basi
$\sqrt{ab}=\sqrt{a·b}$ na $\sqrt{a}·\sqrt{b}=\sqrt{ab}$
Fomu maalum za kuzidisha binomials na conjugates:
$\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}$
Njia ya FOIL inaweza kutumika kuzidisha binomials zenye radicals.

Malengo ya kujifunza

Kumbuka

Kuzidisha mizizi ya Mraba

Ufafanuzi: PRODUCT PROPERTY YA MIZIZI

Mfano9.4.1\PageIndex{1}

Mfano9.4.2\PageIndex{2}

Mfano9.4.3\PageIndex{3}

Mfano9.4.4\PageIndex{4}

Mfano9.4.5\PageIndex{5}

Mfano9.4.6\PageIndex{6}

Mfano9.4.7\PageIndex{7}

Mfano9.4.8\PageIndex{8}

Mfano9.4.9\PageIndex{9}

Mfano9.4.10\PageIndex{10}

Mfano9.4.11\PageIndex{11}

Mfano9.4.12\PageIndex{12}

Mfano9.4.13\PageIndex{13}

Mfano9.4.14\PageIndex{14}

Mfano9.4.15\PageIndex{15}

Ufafanuzi: SQUARING ROOT SQUARE

Mfano9.4.16\PageIndex{16}

Mfano9.4.17\PageIndex{17}

Mfano9.4.18\PageIndex{18}

Tumia Uzidishaji wa Polynomial ili Kuzidisha Mizizi

Mfano9.4.19\PageIndex{19}

Mfano9.4.20\PageIndex{20}

Mfano9.4.21\PageIndex{21}

Mfano9.4.22\PageIndex{22}

Mfano9.4.23\PageIndex{23}

Mfano9.4.24\PageIndex{24}

Mfano9.4.25\PageIndex{25}

Mfano9.4.26\PageIndex{26}

Mfano9.4.27\PageIndex{27}

Mfano9.4.28\PageIndex{28}

Mfano9.4.29\PageIndex{29}

Mfano9.4.30\PageIndex{30}

Mfano9.4.31\PageIndex{31}

Mfano9.4.32\PageIndex{32}

Mfano9.4.33\PageIndex{33}

Mfano9.4.34\PageIndex{34}

Mfano9.4.35\PageIndex{35}

Mfano9.4.36\PageIndex{36}

Ufafanuzi: FORMULA PRODUCT MAALUM

Mfano9.4.37\PageIndex{37}

Mfano9.4.38\PageIndex{38}

Zoezi9.4.39\PageIndex{39}

Mfano9.4.40\PageIndex{40}

Mfano9.4.41\PageIndex{41}

Mfano9.4.42\PageIndex{42}

Mfano9.4.43\PageIndex{43}

Mfano9.4.44\PageIndex{44}

Mfano9.4.45\PageIndex{45}

Mfano9.4.46\PageIndex{46}

Mfano9.4.47\PageIndex{47}

Mfano9.4.48\PageIndex{48}

Dhana muhimu

Mfano $\PageIndex{1}$

Mfano $\PageIndex{2}$

Mfano $\PageIndex{3}$

Mfano $\PageIndex{4}$

Mfano $\PageIndex{5}$

Mfano $\PageIndex{6}$

Mfano $\PageIndex{7}$

Mfano $\PageIndex{8}$

Mfano $\PageIndex{9}$

Mfano $\PageIndex{10}$

Mfano $\PageIndex{11}$

Mfano $\PageIndex{12}$

Mfano $\PageIndex{13}$

Mfano $\PageIndex{14}$

Mfano $\PageIndex{15}$

Mfano $\PageIndex{16}$

Mfano $\PageIndex{17}$

Mfano $\PageIndex{18}$

Mfano $\PageIndex{19}$

Mfano $\PageIndex{20}$

Mfano $\PageIndex{21}$

Mfano $\PageIndex{22}$

Mfano $\PageIndex{23}$

Mfano $\PageIndex{24}$

Mfano $\PageIndex{25}$

Mfano $\PageIndex{26}$

Mfano $\PageIndex{27}$

Mfano $\PageIndex{28}$

Mfano $\PageIndex{29}$

Mfano $\PageIndex{30}$

Mfano $\PageIndex{31}$

Mfano $\PageIndex{32}$

Mfano $\PageIndex{33}$

Mfano $\PageIndex{34}$

Mfano $\PageIndex{35}$

Mfano $\PageIndex{36}$

Mfano $\PageIndex{37}$

Mfano $\PageIndex{38}$

Zoezi $\PageIndex{39}$

Mfano $\PageIndex{40}$

Mfano $\PageIndex{41}$

Mfano $\PageIndex{42}$

Mfano $\PageIndex{43}$

Mfano $\PageIndex{44}$

Mfano $\PageIndex{45}$

Mfano $\PageIndex{46}$

Mfano $\PageIndex{47}$

Mfano $\PageIndex{48}$