9.3E: Mazoezi
- Page ID
- 177403
Mazoezi hufanya kamili
Ongeza na Ondoa Kama Mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
\(8\sqrt{2}−5\sqrt{2}\)
- Jibu
-
\(3\sqrt{2}\)
\(7\sqrt{2}−3\sqrt{2}\)
\(3\sqrt{5}+6\sqrt{5}\)
- Jibu
-
\(9\sqrt{5}\)
\(4\sqrt{5}+8\sqrt{5}\)
\(9\sqrt{7}−10\sqrt{7}\)
- Jibu
-
\(−\sqrt{7}\)
\(11\sqrt{7}−12\sqrt{7}\)
\(7\sqrt{y}+2\sqrt{y}\)
- Jibu
-
\(9\sqrt{y}\)
\(9\sqrt{n}+3\sqrt{n}\)
\(\sqrt{a}−4\sqrt{a}\)
- Jibu
-
\(−3\sqrt{a}\)
\(\sqrt{b}−6\sqrt{b}\)
\(5\sqrt{c}+2\sqrt{c}\)
- Jibu
-
\(7\sqrt{c}\)
\(7\sqrt{d}+2\sqrt{d}\)
\(8\sqrt{a}−2\sqrt{b}\)
- Jibu
-
\(8\sqrt{a}−2\sqrt{b}\)
\(5\sqrt{c}−3\sqrt{d}\)
\(5\sqrt{m}+\sqrt{n}\)
- Jibu
-
\(5\sqrt{m}+\sqrt{n}\)
\(\sqrt{n}+3\sqrt{p}\)
\(8\sqrt{7}+2\sqrt{7}+3\sqrt{7}\)
- Jibu
-
\(13\sqrt{7}\)
\(6\sqrt{5}+3\sqrt{5}+\sqrt{5}\)
\(3\sqrt{11}+2\sqrt{11}−8\sqrt{11}\)
- Jibu
-
\(−3\sqrt{11}\)
\(2\sqrt{15}+5\sqrt{15}−9\sqrt{15}\)
\(3\sqrt{3}−8\sqrt{3}+7\sqrt{5}\)
- Jibu
-
\(−5\sqrt{3}+7\sqrt{5}\)
\(5\sqrt{7}−8\sqrt{7}+6\sqrt{3}\)
\(6\sqrt{2}+2\sqrt{2}−3\sqrt{5}\)
- Jibu
-
\(8\sqrt{2}−3\sqrt{5}\)
\(7\sqrt{5}+\sqrt{5}−8\sqrt{10}\)
\(3\sqrt{2a}−4\sqrt{2a}+5\sqrt{2a}\)
- Jibu
-
\(4\sqrt{2a}\)
\(\sqrt{11b}−5\sqrt{11b}+3\sqrt{11b}\)
\(8\sqrt{3c}+2\sqrt{3c}−9\sqrt{3c}\)
- Jibu
-
\(\sqrt{3c}\)
\(3\sqrt{5d}+8\sqrt{5d}−11\sqrt{5d}\)
\(5\sqrt{3ab}+\sqrt{3ab}−2\sqrt{3ab}\)
- Jibu
-
\ (4\ sqrt {3ab}\
\(8\sqrt{11cd}+5\sqrt{11cd}−9\sqrt{11cd}\)
\(2\sqrt{pq}−5\sqrt{pq}+4\sqrt{pq}\)
- Jibu
-
\(\sqrt{pq}\)
\(11\sqrt{2rs}−9\sqrt{2rs}+3\sqrt{2rs}\)
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{50}+4\sqrt{2}\)
- Jibu
-
\(9\sqrt{2}\)
\(\sqrt{48}+2\sqrt{3}\)
\(\sqrt{80}−3\sqrt{5}\)
- Jibu
-
\(\sqrt{5}\)
\(\sqrt{28}−4\sqrt{7}\)
\(\sqrt{27}−\sqrt{75}\)
- Jibu
-
\(−2\sqrt{3}\)
\(\sqrt{72}−\sqrt{98}\)
\(\sqrt{48}+\sqrt{27}\)
- Jibu
-
\(7\sqrt{3}\)
\(\sqrt{45}+\sqrt{80}\)
\(2\sqrt{50}−3\sqrt{72}\)
- Jibu
-
\(−8\sqrt{2}\)
\(3\sqrt{98}−\sqrt{128}\)
\(2\sqrt{12}+3\sqrt{48}\)
- Jibu
-
\(16\sqrt{3}\)
\(4\sqrt{75}+2\sqrt{108}\)
\(\frac{2}{3}\sqrt{72}+\frac{1}{5}\sqrt{50}\)
- Jibu
-
\(5\sqrt{2}\)
\(\frac{2}{5}\sqrt{75}+\frac{3}{4}\sqrt{48}\)
\(\frac{1}{2}\sqrt{20}−\frac{2}{3}\sqrt{45}\)
- Jibu
-
\(−\sqrt{5}\)
\(\frac{2}{3}\sqrt{54}−\frac{3}{4}\sqrt{96}\)
\(\frac{1}{6}\sqrt{27}−\frac{3}{8}\sqrt{48}\)
- Jibu
-
\(−\sqrt{3}\)
\(\frac{1}{8}\sqrt{32}−\frac{1}{10}\sqrt{50}\)
\(\frac{1}{4}\sqrt{98}−\frac{1}{3}\sqrt{128}\)
- Jibu
-
\(−\frac{3}{4}\sqrt{2}\)
\(\frac{1}{3}\sqrt{24}+\frac{1}{4}\sqrt{54}\)
\(\sqrt{72a^5}−\sqrt{50a^5}\)
- Jibu
-
\(a^2\sqrt{2a}\)
\(\sqrt{48b^5}−\sqrt{75b^5}\)
\(\sqrt{80c^7}−\sqrt{20c^7}\)
- Jibu
-
\(2c^3\sqrt{5c}\)
\(\sqrt{96d^9}−\sqrt{24d^9}\)
\(9\sqrt{80p^4}−6\sqrt{98p^4}\)
- Jibu
-
\(36p^2\sqrt{5}−42p^2\sqrt{2}\)
\(8\sqrt{72q^6}−3\sqrt{75q^6}\)
\(2\sqrt{50r^8}+4\sqrt{54r^8}\)
- Jibu
-
\(10r^4\sqrt{2}+12r^4\sqrt{6}\)
\(5\sqrt{27s^6}+2\sqrt{20s^6}\)
\(3\sqrt{20x^2}−4\sqrt{45x^2}+5x\sqrt{80}\)
- Jibu
-
\(14x\sqrt{5}\)
\(2\sqrt{28x^2}−6\sqrt{3x^2}+6x\sqrt{7}\)
\(3\sqrt{128y^2}+4y\sqrt{162}−8\sqrt{98y^2}\)
- Jibu
-
\(−12y\sqrt{2}\)
\(3\sqrt{75y^2}+8y\sqrt{48}−\sqrt{300y^2}\)
Mazoezi ya mchanganyiko
\(2\sqrt{8}+6\sqrt{8}−5\sqrt{8}\)
- Jibu
-
\(3\sqrt{8}\)
\(\frac{2}{3}\sqrt{27}+\frac{3}{4}\sqrt{48}\)
\(\sqrt{175k^4}−\sqrt{63k^4}\)
- Jibu
-
\(2k^2\sqrt{7}\)
\(\frac{5}{6}\sqrt{162}+\frac{3}{16}\sqrt{128}\)
\(2\sqrt{363}−2\sqrt{300}\)
- Jibu
-
\(2\sqrt{3}\)
\(\sqrt{150}+4\sqrt{6}\)
\(9\sqrt{2}−8\sqrt{2}\)
- Jibu
-
\(\sqrt{2}\)
\(5\sqrt{x}−8\sqrt{y}\)
\(8\sqrt{13}−4\sqrt{13}−3\sqrt{13}\)
- Jibu
-
\(\sqrt{13}\)
\(5\sqrt{12c^4}−3\sqrt{27c^6}\)
\(\sqrt{80a^5}−\sqrt{45a^5}\)
- Jibu
-
\(a^2\sqrt{5a}\)
\(\frac{3}{5}\sqrt{75}−\frac{1}{4}\sqrt{48}\)
\(21\sqrt{19}−2\sqrt{19}\)
- Jibu
-
\(19\sqrt{19}\)
\(\sqrt{500}+\sqrt{405}\)
\(\frac{5}{6}\sqrt{27}+\frac{5}{8}\sqrt{48}\)
- Jibu
-
\(5\sqrt{3}\)
\(11\sqrt{11}−10\sqrt{11}\)
\(\sqrt{75}−\sqrt{108}\)
- Jibu
-
\(−\sqrt{3}\)
\(2\sqrt{98}−4\sqrt{72}\)
\(4\sqrt{24x^2}−\sqrt{54x^2}+3x\sqrt{6}\)
- Jibu
-
\(8x\sqrt{6}\)
\(8\sqrt{80y^6}−6\sqrt{48y^6}\)
kila siku Math
Decorator anaamua kutumia tiles mraba kama strip lafudhi katika kubuni ya kuoga mpya, lakini yeye anataka mzunguko tiles kuangalia kama almasi. Atatumia tiles kubwa 9 zinazopima inchi 8 upande na tiles ndogo 8 zinazopima inchi 2 upande. Tambua upana wa mstari wa msukumo kwa kurahisisha maneno\(9(8\sqrt{2})+8(2\sqrt{2})\). (Pande zote kwa karibu kumi ya inchi.)
- Jibu
-
124.5 inchi
Suzy anataka kutumia tiles mraba juu ya mpaka wa spa yeye ni kufunga katika mashamba yake. Atatumia tiles kubwa ambazo zina eneo la inchi za mraba 12, matofali ya kati ambayo yana eneo la inchi za mraba 8, na tiles ndogo ambazo zina eneo la inchi za mraba 4. Mara baada ya sehemu ya mpaka itahitaji tiles 4 kubwa, tiles 8 kati, na tiles 10 ndogo ili kufikia upana wa ukuta. \(4\sqrt{12}+8\sqrt{8}+10\sqrt{4}\)Kurahisisha maneno ili kuamua upana wa ukuta.
Mazoezi ya kuandika
Eleza tofauti kati ya radicals kama na tofauti na radicals. Hakikisha jibu lako lina maana kwa radicals zenye namba zote mbili na vigezo.
- Jibu
-
Majibu yatatofautiana.
Eleza mchakato wa kuamua kama radicals mbili ni kama au tofauti. Hakikisha jibu lako lina maana kwa radicals zenye namba zote mbili na vigezo.
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
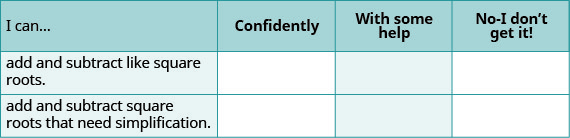
ⓑ Orodha hii inakuambia nini kuhusu ujuzi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?


