Skip to main content
Global

8.9: Tumia Tofauti ya moja kwa moja na Inverse

  1. Last updated
  2. Save as PDF
  • Page ID
    177652

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tatua matatizo ya tofauti ya moja kwa moja
    • Tatua matatizo ya tofauti ya kinyume
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    Ikiwa umepoteza tatizo, rudi kwenye sehemu iliyoorodheshwa na uhakiki nyenzo.

    1. Pata inverse ya kuzidisha ya -8
      Ikiwa umekosa tatizo hili, kagua Zoezi 1.10.13.
    2. Kutatua kwa n: 45=20n
      Kama amekosa tatizo hili, mapitio Zoezi 2.2.1.
    3. Tathmini\(5x^2\) wakati x=10
      Ikiwa umekosa tatizo hili, tathmini Zoezi 1.3.25.

    Wakati kiasi mbili ni kuhusiana na uwiano, tunasema wao ni sawia na kila mmoja. Njia nyingine ya kuelezea uhusiano huu ni kuzungumza juu ya tofauti ya kiasi mbili. Tutajadili tofauti ya moja kwa moja na tofauti tofauti katika sehemu hii.

    Tatua matatizo ya Tofauti ya moja kwa moja

    Lindsay analipwa $15 kwa saa katika kazi yake. Kama sisi basi s kuwa mshahara wake na h kuwa idadi ya masaa yeye amefanya kazi, tunaweza mfano hali hii na equation

    s=15h

    Mshahara wa Lindsay ni bidhaa ya mara kwa mara, 15, na idadi ya masaa anayofanya kazi. Tunasema kwamba mshahara wa Lindsay unatofautiana moja kwa moja na idadi ya masaa anayofanya kazi. Vigezo viwili hutofautiana moja kwa moja ikiwa moja ni bidhaa ya mara kwa mara na nyingine.

    Ufafanuzi: DIRECT TOFAUTI

    Kwa vigezo yoyote mbili x na y, y inatofautiana moja kwa moja na x kama

    y=kx, wapi\(n \ne 0\)

    Katika maombi kwa kutumia tofauti ya moja kwa moja, kwa ujumla sisi kujua maadili ya jozi moja ya vigezo na atatakiwa kupata equation kwamba inahusiana x na y. Basi tunaweza kutumia equation kwamba kupata maadili ya y kwa maadili mengine ya x.

    Jinsi ya Kutatua Matatizo ya Tofauti ya moja kwa moja

    Mfano\(\PageIndex{1}\)

    Kama y inatofautiana moja kwa moja na x na y = 20 wakati x = 8, kupata equation kwamba inahusiana x na y.

    Jibu

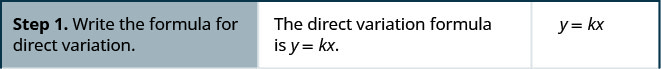
    Picha hapo juu ina nguzo 3. Jedwali linaonyesha hatua za kutatua matatizo ya tofauti ya moja kwa moja. Hatua ya kwanza ni kuandika formula kwa tofauti ya moja kwa moja. moja kwa moja tofauti formula ni y sawa k x Kisha sisi kupata y sawa k mara x.Hatua mbili ni mbadala maadili kutokana na vigezo. Sisi ni kupewa y sawa 20 na x sawa 8. Kisha tuna 20 sawa na mara k 8.Hatua ya tatu ni kutatua kwa tofauti ya mara kwa mara. Gawanya pande zote mbili za equation na 8, kisha uongeze. Sasa tunapata 20 kugawanywa na 8 sawa k K sawa na 2.5.Hatua ya nne ni kuandika equation kwamba inahusiana x na y Rewrite equation jumla na thamani tuligundua k kupata y sawa 2 na tano ya kumi mara x

    Mfano\(\PageIndex{2}\)

    Kama y inatofautiana moja kwa moja kama x na y = 3, wakati x = 10, kupata equation kwamba inahusiana x na y.

    Jibu

    \(y=\frac{3}{10}x\)

    Mfano\(\PageIndex{3}\)

    Kama y inatofautiana moja kwa moja kama x na y = 12 wakati x=4, kupata equation kwamba inahusiana x na y.

    Jibu

    y=3x

    Tutaorodhesha hatua zilizo chini.

    Ufafanuzi: kutatua matatizo ya moja kwa moja
    1. Andika formula kwa tofauti ya moja kwa moja.
    2. Badilisha maadili yaliyotolewa kwa vigezo.
    3. Tatua kwa mara kwa mara ya tofauti.
    4. Andika equation kwamba inahusiana x na y.

    Sasa tutaweza kutatua maombi machache ya tofauti ya moja kwa moja.

    Mfano\(\PageIndex{4}\)

    Wakati Raoul anaendesha kwenye treadmill kwenye mazoezi, idadi ya kalori, c, anachoma inatofautiana moja kwa moja na idadi ya dakika, m, anatumia treadmill. Alichoma kalori 315 alipotumia treadmill kwa dakika 18.

    1. Andika equation inayohusiana c na m.
    2. Je! Angeweza kuchoma kalori ngapi ikiwa alikimbia kwenye treadmill kwa dakika 25?
    Jibu

    1.

      Idadi ya kalori, c inatofautiana moja kwa moja na idadi ya dakika, m, kwenye treadmill, na c=315 wakati m=18
    Andika formula kwa tofauti ya moja kwa moja. .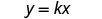
    Tutatumia c badala ya y na mm badala ya x. .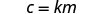
    Badilisha maadili yaliyotolewa kwa vigezo. .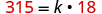
    Tatua kwa mara kwa mara ya tofauti. .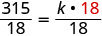
      .
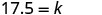
    Andika equation inayohusiana c na m. .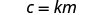
    Mbadala katika mara kwa mara ya tofauti. .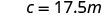

    2.

     

    Kupata c wakati m=25.
    Andika equation inayohusiana c na m. .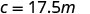
    Badilisha thamani iliyotolewa kwa m. .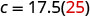
    Kurahisisha. .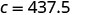
      Raoul angeweza kuchoma kalori 437.5 ikiwa alitumia treadmill kwa dakika 25.
    Mfano\(\PageIndex{5}\)

    Idadi ya kalori, c, kuchomwa hutofautiana moja kwa moja na kiasi cha muda, t, alitumia mazoezi. Arnold kuchomwa kalori 312 katika dakika 65 utumiaji.

    1. Andika equation inayohusiana c na t.
    2. Je! Angeweza kuchoma kalori ngapi ikiwa anafanya mazoezi kwa dakika 90?
    Jibu
    1. c=4.8t
    2. Kalori 432
    Mfano\(\PageIndex{6}\)

    umbali mwili kusonga kusafiri, d, inatofautiana moja kwa moja na wakati, t, ni hatua. Treni husafiri maili 100 katika masaa 2

    1. Andika equation inayohusiana d na t.
    2. Ni maili ngapi ingekuwa kusafiri katika 5 masaa?
    Jibu
    1. d=50t
    2. 250 maili

    Katika mfano uliopita, vigezo c na m viliitwa jina katika tatizo. Kawaida hiyo sivyo. Tutakuwa na jina vigezo katika mfano ijayo kama sehemu ya ufumbuzi, kama sisi kufanya katika matatizo mengi kutumika.

    Mfano\(\PageIndex{7}\)

    Idadi ya galoni ya gesi inayotumia gari la Eunice inatofautiana moja kwa moja na idadi ya maili anayoendesha. Wiki iliyopita alimfukuza maili 469.8 na kutumia galoni 14.5 za gesi.

    1. Andika equation inayohusiana na idadi ya galoni za gesi zinazotumiwa na idadi ya maili zinazoendeshwa.
    2. Ni galoni ngapi za gesi ingekuwa gari la Eunice litatumia kama alimfukuza maili 1000?
    Jibu

    1.

      Idadi ya galoni za gesi inatofautiana moja kwa moja na idadi ya maili zinazoendeshwa.
    Kwanza tutaita jina la vigezo. Hebu g= idadi ya galoni za gesi.
    m= idadi ya maili inaendeshwa.
    Andika formula kwa tofauti ya moja kwa moja. .
    Tutatumia g badala ya y na m badala ya x. .
    Badilisha maadili yaliyotolewa kwa vigezo .
      .
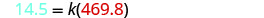
    Tatua kwa mara kwa mara ya tofauti. .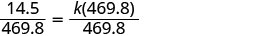
    Tutazunguka kwa elfu ya karibu. .
    Andika equation inayohusiana g na m. .
    Mbadala katika mara kwa mara ya tofauti. .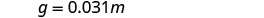

    2.

      Kupata g wakati m=1000.
    Andika equation inayohusiana g na m. g=0.031m
    Badilisha thamani iliyotolewa kwa m. g=0.031 (1000)
    Kurahisisha. g=31
      Gari la Eunice lingetumia galoni 31 za gesi kama aliiendesha maili 1,000.

    Kumbuka kwamba katika mfano huu, vitengo juu ya mara kwa mara ya tofauti ni galoni/maili. Katika maisha ya kila siku, kwa kawaida tunazungumzia kuhusu maili/galoni.

    Mfano\(\PageIndex{8}\)

    Umbali ambao Brad husafiri unatofautiana moja kwa moja na muda uliotumika kusafiri. Brad alisafiri maili 660 katika masaa 12,

    1. Andika equation kwamba inahusiana idadi ya maili kusafiri kwa wakati.
    2. Jinsi maili ngapi inaweza Brad kusafiri katika 4 saa?
    Jibu
    1. m=55h
    2. maili 220
    Mfano\(\PageIndex{9}\)

    Uzito wa kioevu hutofautiana moja kwa moja kama kiasi chake. Kioevu kinachozidi paundi 24 kina kiasi cha galoni 4.

    1. Andika equation inayohusiana na uzito kwa kiasi.
    2. Ikiwa kioevu kina kiasi cha galoni 13, uzito wake ni nini?
    Jibu
    1. w=6v
    2. paundi 78

    Katika hali fulani, variable moja inatofautiana moja kwa moja na mraba wa variable nyingine. Wakati hiyo hutokea, equation ya tofauti ya moja kwa moja ni\(y=kx^2\).

    Mfano\(\PageIndex{10}\)

    Mzigo wa juu boriti itasaidia inatofautiana moja kwa moja na mraba wa uwiano wa sehemu ya msalaba wa boriti. Boriti yenye diagonal “4” itasaidia mzigo mkubwa wa paundi 75.

    1. Andika equation inayohusiana na mzigo wa juu kwa sehemu ya msalaba.
    2. Mzigo wa juu ambao unaweza kuungwa mkono na boriti yenye diagonal 8”?
    Jibu

    1.

      Mzigo wa juu unatofautiana moja kwa moja na mraba wa uwiano wa sehemu ya msalaba.
    Jina la vigezo. Hebu L= mzigo wa kiwango cha juu.
    c= uwiano wa sehemu ya msalaba
    Andika formula kwa tofauti ya moja kwa moja, ambapo y inatofautiana moja kwa moja na mraba wa x. .
    Tutatumia L badala ya y na c badala ya x. .
    Badilisha maadili yaliyotolewa kwa vigezo. .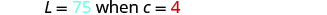
      .
    Tatua kwa mara kwa mara ya tofauti. .
      .
    Andika equation inayohusiana L na c. .
    Mbadala katika mara kwa mara ya tofauti. .

    2.

      Kupata L wakati c=8.
    Andika equation inayohusiana L na c. \(L=4.6875c^2\)
    Badilisha thamani iliyotolewa kwa c. \(L=4.6875(8)^2\)
    Kurahisisha. L=300
      Boriti yenye diagonal “8” inaweza kusaidia mzigo mkubwa wa paundi 300.
    Mfano\(\PageIndex{11}\)

    Umbali kitu kinachoanguka ni sawia moja kwa moja na mraba wa wakati unapoanguka. Mpira unaanguka miguu 144 katika sekunde 3.

    1. Andika equation inayohusiana umbali na wakati.
    2. Je! Kitu kitaanguka mbali gani katika sekunde za 4?
    Jibu
    1. \(d=16t^2\)
    2. Futi 256
    Mfano\(\PageIndex{12}\)

    Eneo la mduara linatofautiana moja kwa moja kama mraba wa radius. Pizza ya mviringo yenye radius ya inchi 6 ina eneo la inchi za mraba 113.04.

    1. Andika equation inayohusiana na eneo hilo kwa radius.
    2. Je! Ni eneo gani la pizza yenye radius ya inchi 9?
    Jibu
    1. \(A=3.14r^2\)
    2. 254.34 inchi za mraba

    Tatua Matatizo ya Tofauti ya Inverse

    Maombi mengi yanahusisha variable mbili ambazo zinatofautiana inversely. Kama ongezeko moja la kutofautiana, nyingine hupungua. Equation kwamba inahusiana nao ni\(y=\frac{k}{x}\).

    Ufafanuzi: TOFAUTI INVERSE

    Kwa vigezo yoyote mbili x na y, y inatofautiana inversely na x kama

    y=\(\frac{k}{x}\), wapi\(k \ne 0\)

    Neno 'inverse' katika tofauti inverse inahusu inverse multiplicative. Inverse multiplicative ya x ni\(\frac{1}{x}\).

    Sisi kutatua matatizo tofauti kinyume kwa njia ile ile sisi kutatuliwa matatizo ya moja kwa moja tofauti. Fomu tu ya jumla ya equation imebadilika. Sisi nakala sanduku utaratibu hapa na tu kubadilisha 'moja kwa moja' na 'inverse'.

    Ufafanuzi: SOLW INVERSE TOFAUTI MATATIZO
    1. Andika formula kwa tofauti ya inverse.
    2. Badilisha maadili yaliyotolewa kwa vigezo.
    3. Tatua kwa mara kwa mara ya tofauti.
    4. Andika equation kwamba inahusiana x na y.
    Mfano\(\PageIndex{13}\)

    Kama y inatofautiana inversely na x na y = 20 wakati x = 8 x na y.

    Jibu
    Andika formula kwa tofauti ya inverse. .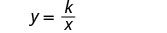
    Badilisha maadili yaliyotolewa kwa vigezo. .
      .
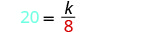
    Tatua kwa mara kwa mara ya tofauti. .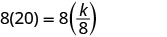
      .
    Andika equation kwamba inahusiana x na y. .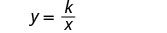
    Mbadala katika mara kwa mara ya tofauti. .
    Mfano\(\PageIndex{14}\)

    Kama p inatofautiana inversely na q na p=30 wakati q = 12 kupata equation kwamba inahusiana p na q.

    Jibu

    \(p=\frac{360}{q}\)

    Mfano\(\PageIndex{15}\)

    Kama y inatofautiana inversely na x na y = 8 wakati x=2 kupata equation kwamba inahusiana x na y.

    Jibu

    \(y=\frac{16}{x}\)

    Mfano\(\PageIndex{16}\)

    Matumizi ya mafuta (mpg) ya gari hutofautiana kinyume na uzito wake. Gari ambalo lina uzito wa paundi 3100 hupata 26 mpg kwenye barabara kuu.

    1. Andika equation ya tofauti.
    2. Je! Matumizi ya mafuta ya gari ambayo yana uzito wa paundi 4030?
    Jibu

    1.

      Matumizi ya mafuta hutofautiana kinyume na uzito.
    Kwanza tutaita jina la vigezo. Hebu f= matumizi ya mafuta.
    w= uzito.
    Andika formula kwa tofauti ya inverse. .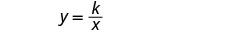
    Tutatumia f badala ya y na sisi badala ya x. .
    Badilisha maadili yaliyotolewa kwa vigezo. .
      .
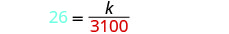
    Tatua kwa mara kwa mara ya tofauti. .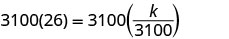
      .
    Andika equation inayohusiana f na w. .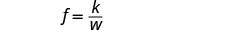
    Mbadala katika mara kwa mara ya tofauti. .

    2.

      Kupata f wakati w=4030.
    Andika equation inayohusiana f na w. .
    Badilisha thamani iliyotolewa kwa w. \(f=\frac{80,600}{4030}\)
    Kurahisisha. f=20
      Gari ambalo lina uzito wa paundi 4030 lingekuwa na matumizi ya mafuta ya mpg 20.
    Mfano\(\PageIndex{17}\)

    Thamani ya gari inatofautiana kinyume na umri wake. Elena alinunua gari la umri wa miaka miwili kwa $20,000.

    1. Andika equation ya tofauti.
    2. Je, itakuwa thamani gani ya gari la Elena wakati wa miaka 5?
    Jibu
    1. \(v=\frac{40,000}{a}\)
    2. $8,000
    Mfano\(\PageIndex{18}\)

    Wakati unaotakiwa kufuta bwawa hutofautiana kinyume kama kiwango cha kusukumia. Ilichukua Lucy masaa 2.5 kumtupia bwawa lake kwa kutumia pampu iliyopimwa saa 400 gpm (galoni kwa dakika).

    1. Andika equation ya tofauti.
    2. Ni muda gani itachukua yake tupu pool kwa kutumia pampu lilipimwa saa 500 gpm?
    Jibu
    1. \(t=\frac{1000}{r}\)
    2. Masaa 2
    Mfano\(\PageIndex{19}\)

    Mzunguko wa kamba ya gitaa hutofautiana kinyume na urefu wake. Kamba ya 26 “ndefu ina mzunguko wa vibrations 440 kwa pili.

    1. Andika equation ya tofauti.
    2. Je, kuna vibrations ngapi kwa pili ikiwa urefu wa kamba umepunguzwa hadi “20” kwa kuweka kidole kwenye fret?
    Jibu

    1.

      Mzunguko hutofautiana kinyume na urefu.
    Jina la vigezo. Hebu f= frequency.
    L=urefu.
    Andika formula kwa tofauti ya inverse. .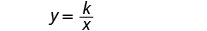
    Tutatumia f badala ya y na L badala ya x .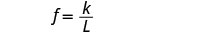
    Badilisha maadili yaliyotolewa kwa vigezo. .
      .
    Tatua kwa mara kwa mara ya tofauti. .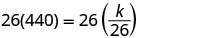
      .
    Andika equation inayohusiana f na L. .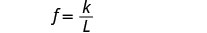
    Mbadala katika mara kwa mara ya tofauti. .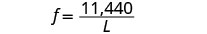

    2.

      Kupata f wakati L = 20.
    Andika equation inayohusiana f na L. \(f=\frac{11,440}{L}\)
    Badilisha thamani iliyotolewa kwa L. \(f=\frac{11,440}{20}\)
    Kurahisisha. f=572
      A 20 “gitaa kamba ina mzunguko 572 vibrations kwa sekunde.
    Mfano\(\PageIndex{20}\)

    Idadi ya masaa inachukua kwa barafu kuyeyuka inatofautiana kinyume na joto la hewa. Tuseme kizuizi cha barafu kinayeyuka katika masaa 2 wakati joto ni digrii 65.

    1. Andika equation ya tofauti.
    2. Je, itachukua saa ngapi kwa kizuizi sawa cha barafu kuyeyuka ikiwa joto lilikuwa digrii 78?
    Jibu
    1. \(h=\frac{130}{t}\)
    2. \(1\frac{2}{3}\)masaa
    Mfano\(\PageIndex{21}\)

    Nguvu inahitajika kuvunja bodi inatofautiana inversely na urefu wake. Richard anatumia paundi 24 za shinikizo kuvunja bodi ya urefu wa mguu 2.

    1. Andika equation ya tofauti.
    2. Ni paundi ngapi za shinikizo zinahitajika kuvunja bodi ya urefu wa mguu wa 5?
    Jibu
    1. \(F=\frac{48}{L}\)
    2. £9.6