8.4E: Mazoezi
- Page ID
- 177758
Mazoezi hufanya kamili
Katika mazoezi yafuatayo, pata LCD.
\(\frac{5}{x^2−2x−8}\),\(\frac{2x}{x^2−x−12}\)
- Jibu
-
(x-4) (x+2) (x+3)
\(\frac{8}{y^2+12y+35}\),\(\frac{3y}{y^2+y−42}\)
\(\frac{9}{z^2+2z−8}\),\(\frac{4z}{z^2−49}\)
- Jibu
-
(z-1) (z+4) (z+2)
\(\frac{6}{a^2+14a+45}\),\(\frac{5a}{a^2−81}\)
\(\frac{4}{b^2+6b+9}\),\(\frac{2b}{b^2−2b−15}\)
- Jibu
-
(b+3) (b+3) (b-5)
\(\frac{5}{c^2−4c+4}\),\(\frac{3c}{c^2−10c+16}\)
\(\frac{2}{3d^2+14d−5}\),\(\frac{5d}{3d^2−19d+6}\)
- Jibu
-
(3d-1) (d+5) (d-6)
\(\frac{3}{5m^2−3m−2}\),\(\frac{6m}{5m^2+17m+6}\)
Katika mazoezi yafuatayo, andika kama maneno sawa ya busara na LCD iliyotolewa.
\(\frac{5}{x^2−2x−8}\),\(\frac{2x}{x^2−x−12}\)
LCD (x-4) (x+2) (x+3)
- Jibu
-
\(\frac{5x+15}{(x−4)(x+2)(x+3)}\),
\(\frac{2x^2+4x}{(x−4)(x+2)(x+3)}\)
\(\frac{8}{y^2+12y+35}\),\(\frac{3y}{y^2+y−42}\)
LCD (y+7) (y+5) (y-6)
\(\frac{9}{z^2+2z−8}\),\(\frac{4z}{z^2−49}\)
LCD (z-2) (z+4) (z+2)
- Jibu
-
\(\frac{9z+18}{(z−2)(z+4)(z+2)}\),
\(\frac{4z^2+16}{(z−2)(z+4)(z+2)}\)
\(\frac{6}{a^2+14a+45}\),\(\frac{5a}{a^2−81}\)
LCD (a+9) (a+5) (a-9)
\(\frac{4}{b^2+6b+9}\),\(\frac{2b}{b^2−2b−15}\)
LCD (b+3) (b+3) (b-5)
- Jibu
-
\(\frac{4b−20}{(b+3)(b+3)(b−5)}\),
\(\frac{2b^2+6b}{(b+3)(b+3)(b−5)}\)
\(\frac{5}{c^2−4c+4}\),\(\frac{3c}{c^2−10c+10}\)
LCD (c-2) (c-1) (c-8)
\(\frac{2}{3d^2+14d−5}\),\(\frac{5d}{3d^2−19d+6}\)
LCD (3d-1) (d+5) (d-6)
- Jibu
-
\(\frac{2d−12}{(3d−1)(d+5)(d−6)}\),
\(\frac{5d^2+25d}{(3d−1)(d+5)(d−6)}\)
\(\frac{3}{5m^2−3m−2}\),\(\frac{6m}{5m^2+17m+6}\)
LCD (5m+2) (m-1) (m+3)
Katika mazoezi yafuatayo, ongeza.
\(\frac{5}{24}+\frac{11}{36}\)
- Jibu
-
\(\frac{37}{72}\)
\(\frac{7}{30}+\frac{13}{45}\)
\(\frac{9}{20}+\frac{11}{30}\)
- Jibu
-
\(\frac{49}{60}\)
\(\frac{8}{27}+\frac{7}{18}\)
\(\frac{7}{10x^{2}y}+\frac{4}{15xy^2}\)
- Jibu
-
\(\frac{21y+8x}{30x^{2}y^2}\)
\(\frac{1}{12a^{3}b^2}+\frac{5}{9a^{2}b^3}\)
\(\frac{1}{2m}+\frac{7}{8m^{2}n}\)
- Jibu
-
\(\frac{mn+14}{16m^{2}n}\)
\(\frac{5}{6p^{2}q}+\frac{1}{4p}\)
\(\frac{3}{r+4}+\frac{2}{r−5}\)
- Jibu
-
\(\frac{5r−7}{(r+4)(r−5)}\)
\(\frac{4}{s−7}+\frac{5}{s+3}\)
\(\frac{8}{t+5}+\frac{6}{t−5}\)
- Jibu
-
\(\frac{14t−10}{(t+5)(t−5)}\)
\(\frac{7}{v+5}+\frac{9}{v−5}\)
\(\frac{5}{3w−2}+\frac{2}{w+1}\)
- Jibu
-
\(\frac{11w+1}{(3w−2)(w+1)}\)
\(\frac{4}{2x+5}+\frac{2}{x−14}\)
\(\frac{2y}{y+3}+\frac{3}{y−12}\)
- Jibu
-
\(\frac{2y^2+y+9}{(y+3)(y−1)}\)
\(\frac{3z}{z−2}+\frac{1}{z+5}\)
\(\frac{5b}{a^2b−2a^2}+\frac{2b}{b^2−4}\)
- Jibu
-
\(\frac{b(5b+10+2a2)}{a^2(b−2)(b+2)}\)
\(\frac{4}{cd+3c}+\frac{1}{d^2−9}\)
\(\frac{2m}{3m−3}+\frac{5m}{m^2+3m−4}\)
- Jibu
-
\(\frac{2m^2+23m}{3(m−1)(m+4)}\)
\(\frac{3}{4n+4}+\frac{6}{n^2−n−2}\)
\(\frac{3}{n^2+3n−18}+\frac{4n}{n^2+8n+12}\)
- Jibu
-
\(\frac{4n^2−9n+6}{(n-3)(n+6)(n+2)}\)
\(\frac{6}{q^2−3q−10}+\frac{5q}{q^2−8q+15}\)
\(\frac{3r}{r^2+7r+6}+\frac{9}{r^2+4r+3}\)
- Jibu
-
\(\frac{3(r^2+6r+18)}{(r+1)(r+6)(r+3)}\)
\(\frac{2s}{s^2+2s−8}+\frac{4}{s^2+3s−10}\)
Katika mazoezi yafuatayo, toa.
\(\frac{t}{t−6}−\frac{t−2}{t+6}\)
- Jibu
-
\(\frac{2(7t−6)}{(t−6)(t+6)}\)
\(\frac{v}{v−3}−\frac{v−6}{v+1}\)
\(\frac{w+2}{w+4}−\frac{w}{w−2}\)
- Jibu
-
\(\frac{−4(1+w)}{(w+4)(w−2)}\)
\(\frac{x−3}{x+6}−\frac{x}{x+3}\)
\(\frac{y−4}{y+1}−\frac{1}{y+7}\)
- Jibu
-
\(\frac{y^2+2y-29}{(y+1)(y+7)}\)
\(\frac{z+8}{z−3}−\frac{z}{z−2}\)
\(\frac{5a}{a+3}−\frac{a+2}{a+6}\)
- Jibu
-
\(\frac{4a^2+25a−6}{(a+3)(a+6)}\)
\(\frac{3b}{b−2}−\frac{b−6}{b−8}\)
\(\frac{6c}{c^2−25}−\frac{3}{c+5}\)
- Jibu
-
\(\frac{3}{c−5}\)
\(\frac{4d}{d^2−81}−\frac{2}{d+9}\)
\(\frac{6}{m+6}−\frac{12m}{m^2−36}\)
- Jibu
-
\(\frac{−6}{m−6}\)
\(\frac{4}{n+4}−\frac{8n}{n^2−16}\)
\(\frac{−9p−17}{p^2−4p−21}−\frac{p+1}{7−p}\)
- Jibu
-
\(\frac{p+2}{p+3}\)
\(\frac{7q+8}{q^2−2q−24}−\frac{q+2}{4−q}\)
\(\frac{−2r−16}{r^2+6r−16}−\frac{5}{2−r}\)
- Jibu
-
\(\frac{3}{r−2}\)
\(\frac{2t−30}{t^2+6t−27}−\frac{2}{3−t}\)
\(\frac{5v−2}{v+3}−4\)
- Jibu
-
\(\frac{−v−14}{v+3}\)
\(\frac{6w+5}{w−1}+2\)
\(\frac{2x+7}{10x−1}+3\)
- Jibu
-
\(\frac{4(8x+1)}{10x−1}\)
\(\frac{8y−4}{5y+2}−6\)
Katika mazoezi yafuatayo, ongeza na uondoe.
\(\frac{5a}{a−2}+\frac{9}{a}−\frac{2a+18}{a^2−2a}\)
- Jibu
-
\(\frac{5a^2+7a−36}{a(a−2)}\)
\(\frac{2b}{b−5}+\frac{3}{2b}−\frac{2}{b−15}\)
\(\frac{c}{c+2}+\frac{5}{c−2}−\frac{10c}{c^2−4}\)
- Jibu
-
\(\frac{c−5}{c+2}\)
\(\frac{6d}{d−5}+\frac{1}{d+4}−\frac{7d−5}{d^2−d−20}\)
Katika mazoezi yafuatayo, kurahisisha.
\(\frac{6a}{3ab+b^2}+\frac{3a}{9a^2−b^2}\)
- Jibu
-
\(\frac{3a(6a−b)}{b(3a+b)(3a−b)}\)
\(\frac{2c}{2c+10}+\frac{7c}{c^2+9c+20}\)
\(\frac{6d}{d^2−64}−\frac{3}{d−8}\)
- Jibu
-
\(\frac{3}{d+8}\)
\(\frac{5}{n+7}−\frac{10n}{n^2−49}\)
\(\frac{4m}{m^2+6m−7}+\frac{2}{m^2+10m+21}\)
- Jibu
-
\(\frac{2(2m^2+7m−1)}{(m+7)(m−1)(m+3)}\)
\(\frac{3p}{p^2+4p−12}+\frac{1}{p^2+p−30}\)
\(\frac{−5n−5}{n^2+n−6}+\frac{n+1}{2−n}\)
- Jibu
-
\(\frac{n+1}{n+3}\)
\(\frac{−4b−24}{b^2+b−30}+\frac{b+7}{5−b}\)
\(\frac{7}{15p}+\frac{5}{18pq}\)
- Jibu
-
\(\frac{42q+25}{90pq}\)
\(\frac{3}{20a^2}+\frac{11}{12ab^2}\)
\(\frac{4}{x−2}+\frac{3}{x+5}\)
- Jibu
-
\(\frac{7(x+2)}{(x−2)(x+5)}\)
\(\frac{6}{m+4}+\frac{9}{m−8}\)
\(\frac{2q+7}{y+4}−2\)
- Jibu
-
\(\frac{17q+2}{3q−1}\)
\(\frac{3y−1}{y+4}−2\)
\(\frac{z+2}{z−5}−\frac{z}{z+1}\)
- Jibu
-
\(\frac{8z+2}{(z−5)(z+1)}\)
\(\frac{t}{t−5}−\frac{t−1}{t+5}\)
\(\frac{3d}{d+2}+\frac{4}{d}−\frac{d+8}{d^2+2d}\)
- Jibu
-
\(\frac{3(d+1)}{d+2}\)
\(\frac{2q}{q+5}+\frac{3}{q−3}−\frac{13q+15}{q^2+2q−15}\)
kila siku Math
Mapambo cupcakes Victoria inaweza kupamba amri ya cupcakes kwa ajili ya harusi katika masaa tt, hivyo katika saa 1 anaweza kupamba\(\frac{1}{t}\) ya cupcakes. Itachukua dada yake masaa 3 tena kupamba utaratibu huo wa cupcakes, hivyo katika saa 1 anaweza kupamba\(\frac{1}{t+3}\) ya cupcakes.
- Pata sehemu ya kazi ya mapambo ambayo Victoria na dada yake, wakifanya kazi pamoja, wangekamilisha saa moja kwa kuongeza maneno ya busara\(\frac{1}{t}+\frac{1}{t+3}\).
- Tathmini jibu lako kwa sehemu (a) wakati t=5.
- Jibu
-
- \(\frac{2t+3}{t(t+3)}\)
- \(\frac{13}{40}\)
Kayaking Wakati Trina kayaks upriver, inachukua\(\frac{5}{3−c}\) masaa yake kwenda 5 maili, ambapo cc ni kasi ya mto sasa. Inachukua\(\frac{5}{3+c}\) masaa yake kwa Kayak 5 maili chini ya mto.
- Kupata kujieleza kwa idadi ya masaa itachukua Trina kwa Kayak 5 maili juu ya mto na kisha kurudi kwa kuongeza\(\frac{5}{3−c}+\frac{5}{3+c}\).
- Tathmini jibu lako kwa sehemu (a) wakati c=1 ili kupata idadi ya masaa itachukua Trina ikiwa kasi ya mto wa sasa ni maili 1 kwa saa.
Mazoezi ya kuandika
Felipe anadhani\(\frac{1}{x}+\frac{1}{y}\) ni\(\frac{2}{x+y}\).
- Chagua maadili ya namba kwa x na y na tathmini\(\frac{1}{x}+\frac{1}{y}\).
- Tathmini\(\frac{2}{x+y}\) kwa maadili sawa ya x na y uliyotumia sehemu (a).
- Eleza kwa nini Felipe ni makosa.
- Kupata kujieleza sahihi kwa\(\frac{1}{x}+\frac{1}{y}\).
- Jibu
-
Majibu yanaweza kutofautiana.
Kurahisisha maneno\(\frac{4}{n^2+6n+9}−\frac{1}{n^2−9}\) na kuelezea hatua zako zote.
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
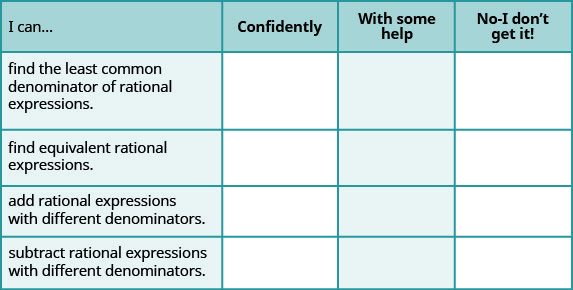
ⓑ Kwa kiwango cha 1-10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?


