Skip to main content
Global

8.4: Ongeza na Ondoa Maneno ya busara na Denominators tofauti

  1. Last updated
  2. Save as PDF
  • Page ID
    177746

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Find denominator angalau ya kawaida ya maneno ya busara
    • Pata maneno sawa ya busara
    • Ongeza maneno ya busara na madhehebu tofauti
    • Ondoa maneno ya busara na madhehebu tofauti
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    Ikiwa umepoteza tatizo, rudi kwenye sehemu iliyoorodheshwa na uhakiki nyenzo.

    1. Ongeza:\(\frac{7}{10}+\frac{8}{15}\).
      Kama amekosa tatizo hili, kupitia Zoezi 1.7.13.
    2. Ondoa:\(6(2x+1)−4(x−5)\).
      Kama amekosa tatizo hili, mapitio Zoezi 1.10.52.
    3. Kupata Greatest Common Factor ya\(9x^{2}y^{3}\) na\(12xy^{5}\)
      Kama amekosa tatizo hili, mapitio Zoezi 7.1.7.
    4. Sababu kabisa -48n-12
      Ikiwa umekosa tatizo hili, kagua Zoezi 7.1.31.

    Pata Denominator ya kawaida ya maneno ya busara

    Tunapoongeza au kuondoa maneno ya busara na tofauti na denominators tutahitaji kupata denominators ya kawaida. Ikiwa tunapitia utaratibu tuliotumia kwa sehemu ndogo za namba, tutajua nini cha kufanya na maneno ya busara.

    Hebu tuangalie mfano\(\frac{7}{12}+\frac{5}{18}\) kutoka Misingi. Kwa kuwa denominators si sawa, hatua ya kwanza ilikuwa kupata denominator ya kawaida (LCD). Kumbuka, LCD ni angalau kawaida nyingi ya denominators. Ni idadi ndogo tunaweza kutumia kama denominator ya kawaida.

    Ili kupata LCD ya 12 na 18, tuliweka kila nambari katika primes, tukiweka safu yoyote ya kawaida katika nguzo. Kisha sisi “tulileta” mkuu mmoja kutoka kila safu. Hatimaye, tuliongeza sababu za kupata LCD.

    12=2·2·3

    18=2·3·3

    LCD=2·2·3·3

    LCD=36

    Tunafanya kitu kimoja kwa maneno ya busara. Hata hivyo, sisi kuondoka LCD katika fomu factored.

    Ufafanuzi: FIND DENOMINATOR ANGALAU YA MANENO YA busara.
    1. Factor kila kujieleza kabisa.
    2. Orodha ya mambo ya kila kujieleza. Mechi sababu wima ikiwezekana.
    3. Kuleta chini nguzo.
    4. Panua mambo.

    Kumbuka, sisi daima hutenganisha maadili ambayo yangeweza kufanya sifuri ya denominator. Ni maadili gani ya xv tunapaswa kuwatenga katika mfano huu ujao?

    Mfano\(\PageIndex{1}\)

    Kupata LCD kwa\(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\)

    Jibu
      \(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\)
    Fanya kila kujieleza kabisa, kuunganisha mambo ya kawaida. Kuleta chini nguzo. \(x^2−2x−3=(x−3)(x+1)\)
      \(x^2+4x+3=(x+1)(x+3)\)
    Panua mambo. LCD= (x+1) (x-3) (x+3)
      LCD ni (x+1) (x-1) (x-3) (x+3).
    Mfano\(\PageIndex{2}\)

    Kupata LCD kwa\(\frac{2}{x^2−x−12},\frac{1}{x^2−16}\)

    Jibu

    (x-4) (x+4) (x+3)

    Mfano\(\PageIndex{3}\)

    Kupata LCD kwa\(\frac{x}{x^2+8x+15},\frac{5}{x^2+9x+18}\)

    Jibu

    (x+3) (x+6) (x+5)

    Pata Maneno sawa ya busara

    Tunapoongeza sehemu ndogo za namba, mara tu tunapopata LCD, tunaandika upya kila sehemu kama sehemu sawa na LCD.

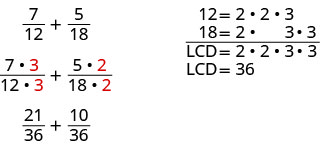
    Picha hapo juu inaonyesha jinsi ya kupata LCD (denominator isiyo ya kawaida) wakati wa kuongeza sehemu ndogo za namba katika mfano saba kumi na mbili pamoja na tano na nane. Picha inaonyesha mara 7 3 imegawanywa na mara 12 3 pamoja na mara 5 2 pamoja na mara 18 2. Chini ya hii ni 21 imegawanywa na 36 pamoja na 10 imegawanywa na 36. Picha iliyo karibu na hii inaonyesha kwamba 12 ni sawa na mara 2 mara 3. Chini hii inaonyesha 18 sawa 2 mara 3 mara 3. Mstari hutolewa. Chini ni LCD sawa mara 2 mara 3 mara 3. Mstari hapa chini hii inaonyesha kwamba LCD ni sawa na 36.

    Tutafanya kitu kimoja kwa maneno ya busara.

    Mfano\(\PageIndex{4}\)

    Andika upya kama maneno sawa ya busara na denominator (x+1) (x-1) (x+3):\(\frac{8}{x^2−2x−3}\),\(\frac{3x}{x^2+4x+3}\).

    Jibu
      .
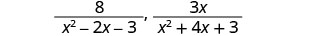
    Factor kila denominator. .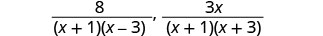
    Kupata LCD. .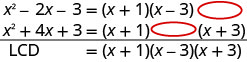  
    Kuzidisha kila denominator kwa sababu 'kukosa' na kuzidisha kila nambari kwa sababu sawa. .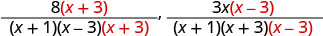
    Kurahisisha nambari. .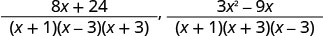
    Mfano\(\PageIndex{5}\)

    Andika upya kama maneno sawa ya busara na denominator (x+3) (x-4) (x+4):
    \(\frac{2}{x^2−x−12}\),\(\frac{1}{x^2−16}\).

    Jibu

    \(\frac{2x+8}{(x−4)(x+3)(x+4)}\),
    \(\frac{x+3}{(x−4)(x+3)(x+4)}\)

    Mfano\(\PageIndex{6}\)

    Andika upya kama maneno sawa ya busara na denominator (x+3) (x+5) (x+6)
    \(\frac{x}{x^2+8x+15}\),\(\frac{5}{x^2+9x+18}\).

    Jibu

    \(\frac{x^2+6x}{(x+3)(x+5)(x+6)}\),
    \(\frac{x+3}{(x+3)(x+5)(x+6)}\)

    Ongeza Maneno ya busara na madhehebu tofauti

    Sasa tuna hatua zote tunayohitaji kuongeza maneno ya busara na madhehebu tofauti. Kama tulivyofanya hapo awali, tutafanya mfano mmoja wa kuongeza sehemu ndogo za namba kwanza.

    Mfano\(\PageIndex{7}\)

    Ongeza:\(\frac{7}{12}+\frac{5}{18}\).

    Jibu
      .
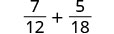
    Kupata LCD ya 12 na 18. .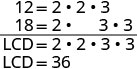  
    Andika upya kila sehemu kama sehemu sawa na LCD. .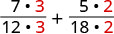
    Ongeza sehemu ndogo. .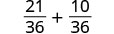
    Sehemu haiwezi kuwa rahisi. .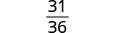
    Mfano\(\PageIndex{8}\)

    Ongeza:\(\frac{11}{30}+\frac{7}{12}\).

    Jibu

    \(\frac{19}{20}\)

    Mfano\(\PageIndex{9}\)

    Ongeza:\(\frac{3}{8}+\frac{9}{20}\).

    Jibu

    \(\frac{33}{40}\)

    Sasa tutaongeza maneno ya busara ambayo denominators ni monomials.

    Mfano\(\PageIndex{10}\)

    Ongeza:\(\frac{5}{12x^{2}y}+\frac{4}{21xy^2}\).

    Jibu
      .

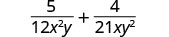
    Kupata LCD ya\(12x^{2}y\) na\(21xy^2\).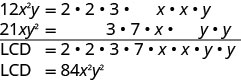    		  
      .
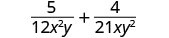
    Andika upya kila kujieleza kwa busara kama sehemu sawa na LCD. .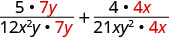
    Kurahisisha. .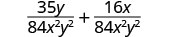
    Ongeza maneno ya busara. .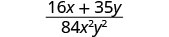
    Hakuna mambo ya kawaida kwa nambari na denominator. Sehemu haiwezi kuwa rahisi.  
    Mfano\(\PageIndex{11}\)

    Ongeza:\(\frac{2}{15a^{2}b}+\frac{5}{6ab^2}\).

    Jibu

    \(\frac{4b+25a}{30a^{2}b^2}\)

    Mfano\(\PageIndex{12}\)

    Ongeza:\(\frac{5}{16c}+\frac{3}{8cd^2}\).

    Jibu

    \(\frac{5d^2+6}{16cd^2}\)

    Sasa tuko tayari kukabiliana na madhehebu ya polynomial.

    Jinsi ya Kuongeza Maneno ya busara na Denominators tofauti

    Mfano\(\PageIndex{13}\)

    Ongeza:\(\frac{3}{x−3}+\frac{2}{x−2}\).

    Jibu

    Picha hapo juu inaonyesha hatua za kuongeza sehemu ambazo denominators ni monomials kwa mfano 5 imegawanywa na 12 x squared y pamoja 4 imegawanywa na 21 x y squared. Pata LCD ya 12 x squared y na 21 x y squared. Na haki ya kujieleza hii ni 12 x squared y sawa mara 2 mara 2 mara x mara y. chini kwamba ni 21 x y squared sawa mara 3 mara 7 x mara y y. line ni inayotolewa. Chini ya kwamba ni LCD sawa mara 2 mara 2 mara 3 mara 7 x mara x mara y chini kwamba ni LCD sawa 84 x squared y squared. Andika upya kila kujieleza kwa busara kama sehemu sawa na LCD. Equation ya awali inavyoonyeshwa. Chini ya hiyo ni mara 5 7 y imegawanywa na 12 x squared y mara 7 y pamoja na mara 4 4 x kugawanywa na 21 x y mara mraba 4 x Kurahisisha kupata 35 y kugawanywa na 84 x squared y squared pamoja 16 x kugawanywa na x squared y squared. Ongeza maneno ya busara 16 x pamoja na 35 y imegawanywa na 84 x squared y squared. Hakuna mambo ya kawaida kwa nambari na denominator. Sehemu haiwezi kuwa rahisi.Hatua ya 2 ni kuongeza kujieleza kwa busara. Kisha, ongeza nambari na uweke jumla juu ya denominator ya kawaida ili kupata 3 x minus 6 pamoja na 2 x minus 6 imegawanywa na x minus mara 3 x bala 2.Hatua ya 3 ni kurahisisha, ikiwa inawezekana. Kwa sababu 5 x minus 12 haiwezi kuhesabiwa, jibu ni rahisi kwa 5 x minus 12 kugawanywa na x minus mara 3 x minus 2.

    Mfano\(\PageIndex{14}\)

    Ongeza:\(\frac{2}{x−2}+\frac{5}{x+3}\).

    Jibu

    \(\frac{7x−4}{(x+3)(x−2)}\)

    Mfano\(\PageIndex{15}\)

    Ongeza:\(\frac{4}{m+3}+\frac{3}{m+4}\).

    Jibu

    \(\frac{7m+25}{(m+3)(m+4)}\)

    Hatua za kutumia ili kuongeza maneno ya busara zinafupishwa katika sanduku la utaratibu wafuatayo.

    Ufafanuzi: ONGEZA MANENO YA MANENO.
    1. Kuamua kama maneno yana denominator ya kawaida.
      Ndiyo — nenda hatua ya 2.
      Hapana — Andika upya kila kujieleza mantiki na LCD.
      Kupata LCD.
      Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD.
    2. Ongeza maneno ya busara.
    3. Kurahisisha, ikiwa inawezekana.
    Mfano\(\PageIndex{16}\)

    Ongeza:\(\frac{2a}{2ab+b^2}+\frac{3a}{4a^2−b^2}\).

    Jibu
      .
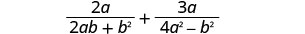
    Je, maneno yana denominator ya kawaida? Hapana.
    Andika upya kila kujieleza na LCD.    		  
    Kupata LCD. .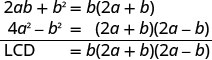  
    Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD. .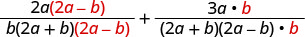
    Kurahisisha nambari. .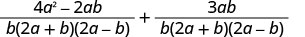
    Ongeza maneno ya busara. .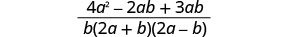
    Kurahisisha nambari. .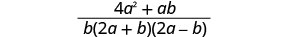
    Fanya namba. .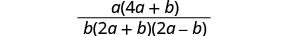
    Hakuna mambo ya kawaida kwa nambari na denominator. Sehemu haiwezi kuwa rahisi.  
    Mfano\(\PageIndex{17}\)

    Ongeza:\(\frac{5x}{xy−y^2}+\frac{2x}{x^2+y^2}\).

    Jibu

    \(\frac{x(5x+7y)}{y(x−y)(x+y)}\)

    Mfano\(\PageIndex{18}\)

    Ongeza:\(\frac{7}{2m+6}+\frac{4}{m^2+4m+3}\).

    Jibu

    \(\frac{7m+15}{2(m+3)(m+1)}\)

    Epuka majaribu ya kurahisisha hivi karibuni! Katika mfano hapo juu, tunapaswa kuondoka kujieleza kwanza kwa busara kama\(\frac{2a(2a−b)}{b(2a+b)(2a−b)}\) to be able to add it to \(\frac{3a·b}{(2a+b)(2a−b)·b}\).

    Mfano\(\PageIndex{19}\)

    Ongeza:\(\frac{8}{x^2−2x−3}+\frac{3x}{x^2+4x+3}\).

    Jibu
      .
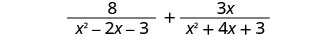
    Je, maneno yana denominator ya kawaida? Hapana.
    Andika upya kila kujieleza na LCD.    		  
    Kupata LCD. .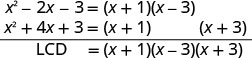  
    Andika upya kila kujieleza kwa busara kama sehemu sawa na LCD. .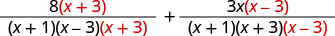
    Kurahisisha nambari. .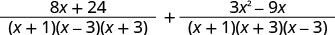
    Ongeza maneno ya busara. .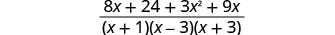
    Kurahisisha nambari. .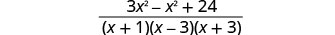
    Nambari ni mkuu, kwa hiyo hakuna sababu za kawaida.  
    Mfano\(\PageIndex{20}\)

    Ongeza:\(\frac{1}{m^2−m−2}+\frac{5m}{m^2+3m+2}\).

    Jibu

    \(\frac{5m^2−9m+2}{(m−2)(m+1)(m+2)}\)

    Mfano\(\PageIndex{21}\)

    Ongeza:\(\frac{2n}{n^2−3n−10}+\frac{6}{n^2+5n+6}\).

    Jibu

    \(\frac{2(n2+6n−15)}{(n+2)(n−5)(n+3)}\)

    Ondoa Maneno ya busara na Denominators tofauti

    Mchakato tunayotumia kuondoa maneno ya busara na denominators tofauti ni sawa na kwa kuongeza. Tunapaswa tu kuwa makini sana kwa ishara wakati wa kuondoa nambari.

    Jinsi ya Kuondoa Maneno ya busara na Denominators tofauti

    Mfano\(\PageIndex{22}\)

    Ondoa:\(\frac{x}{x−3}−\frac{x−2}{x+3}\).

    Jibu

    Picha hapo juu ina nguzo 3. Inaonyesha hatua za jinsi ya kuondoa maneno ya busara na denominators tofauti kwa x imegawanywa na x minus tatu bala x pamoja x minus 3. Hatua ya 1 ni Kuamua kama maneno yana denominator ya kawaida. Ndiyo — nenda hatua ya 2. Hapana — Andika upya kila kujieleza mantiki na LCD. Kupata LCD. Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD. Katika maneno hapo juu, jibu ni hapana. Pata LCD ya x minus 3, x pamoja na 3. Na haki ya hii ni x - 3: x - 3. Chini kwamba ni x - 2: x - 2. Mstari hutolewa. Chini ya kwamba imeandikwa LCD ni x — 3 mara x plus 3. Andika upya kama x mara x pamoja na 3 imegawanywa na x minus mara 3 x pamoja 3 minus x minus mara 2 x minus 3 imegawanywa na x pamoja mara 3 x minus 3. Keep denominators factored! Sababu ya kupata x mraba pamoja na 3 x imegawanywa na x bala mara 3 x pamoja na 3 minus x squared minus 5 x plus 6 imegawanywa na x minus mara 3 x pamoja 3.Hatua ya 2 ni kuondoa maneno ya busara. Ondoa nambari na uweke tofauti juu ya denominator ya kawaida ili kupata x 2 pamoja na 3 x bala x x mraba bala 5 x pamoja 6 imegawanywa na x bala mara 3 x pamoja 3. Kisha kwa x mraba pamoja na 3 x minus x squared pamoja 5 x minus 6 imegawanywa na x minus mara 3 x pamoja 3. Kuwa makini na ishara! Kisha hadi 8 x minus 6 imegawanywa na x minus mara 3 x pamoja 3.Hatua ya 3 ni kurahisisha, ikiwa inawezekana. Nambari na denominator hazina sababu sawa. Jibu ni rahisi kwa mara 2 4 x minus 3 imegawanywa na x minus mara 3 x pamoja 3.

    Mfano\(\PageIndex{23}\)

    Ondoa:\(\frac{y}{y+4}−\frac{y−2}{y−5}\).

    Jibu

    \(\frac{−7y+8}{(y+4)(y−5)}\)

    Mfano\(\PageIndex{24}\)

    Ondoa:\(\frac{z+3}{z+2}−\frac{z}{z+3}\).

    Jibu

    \(\frac{4z+9}{(z+2)(z+3)}\)

    Hatua za kuchukua ili kuondoa maneno ya busara zimeorodheshwa hapa chini.

    Ufafanuzi: Ondoa MANENO YA MANENO.
    1. Kuamua kama wana denominator ya kawaida.
      Ndiyo — nenda hatua ya 2.
      Hapana — Andika upya kila kujieleza mantiki na LCD.
      Kupata LCD.
      Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD.
    2. Ondoa maneno ya busara.
    3. Kurahisisha, ikiwa inawezekana.
    Mfano\(\PageIndex{25}\)

    Ondoa:\(\frac{8y}{y^2−16}−\frac{4}{y−4}\).

    Jibu
      .
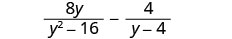
    Je, maneno yana denominator ya kawaida? Hapana.
    Andika upya kila kujieleza na LCD.    		  
    Kupata LCD. .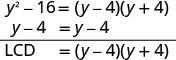  
    Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD. .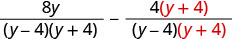
    Kurahisisha nambari. .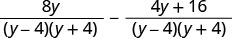
    Ondoa maneno ya busara. .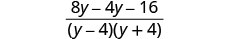
    Kurahisisha nambari. .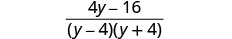
    Fanya namba ya kuangalia mambo ya kawaida. .
    Ondoa mambo ya kawaida. .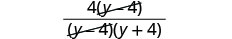
    Kurahisisha. .
    Mfano\(\PageIndex{26}\)

    Ondoa:\(\frac{2x}{x^2−4}−\frac{1}{x+2}\).

    Jibu

    \(\frac{1}{x−2}\)

    Mfano\(\PageIndex{27}\)

    Ondoa:\(\frac{3}{z+3}−\frac{6z}{z^2−9}\).

    Jibu

    \(\frac{−3}{z−3}\)

    Kuna ishara nyingi hasi katika mfano unaofuata. Kuwa makini zaidi!

    Mfano\(\PageIndex{28}\)

    Ondoa:\(\frac{−3n−9}{n^2+n−6}−\frac{n+3}{2−n}\).

    Jibu
      .
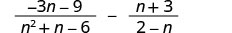
    Sababu ya denominator. .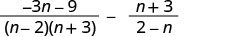
    Kwa kuwa n-1 na 2—n ni kinyume, tutazidisha maneno ya pili ya busara na\(\frac{−1}{−1}\). .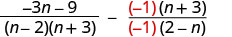
    Kurahisisha. .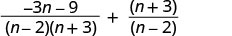
    Je, maneno yana denominator ya kawaida? Hapana.  
    Kupata LCD. .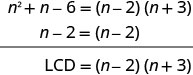  
    Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD. .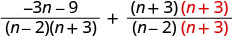
    Kurahisisha nambari. .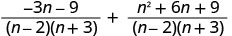
    Kurahisisha maneno ya busara. .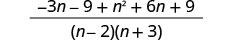
    Kurahisisha nambari. .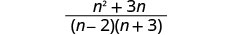
    Fanya namba ya kuangalia mambo ya kawaida. .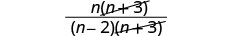
    Kurahisisha. .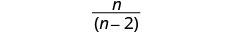
    Mfano\(\PageIndex{29}\)

    Ondoa:\(\frac{3x−1}{x^2−5x−6}−\frac{2}{6−x}\).

    Jibu

    \(\frac{1}{x−6}\)

    Mfano\(\PageIndex{30}\)

    Ondoa:\(\frac{−2y−2}{y^2+2y−8}−\frac{y−1}{2−y}\).

    Jibu

    \(\frac{y+3}{y+4}\)

    Wakati kujieleza moja si katika sehemu fomu, tunaweza kuandika kama sehemu na denominator 1.

    Mfano\(\PageIndex{31}\)

    Ondoa:\(\frac{5c+4}{c−2}−3\).

    Jibu
      .
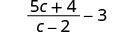
    Andika 3 kama\(\frac{3}{1}\) kuwa na maneno 2 ya busara. .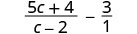
    Je! Maneno ya busara yana denominator ya kawaida? Hapana.  
    Kupata LCD ya c-1 na 1. LCD = c-1.
    Andika upya\(\frac{3}{1}\) kama kujieleza sawa na LCD. .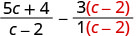
    Kurahisisha. .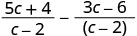
    Ondoa maneno ya busara. .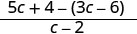
    Kurahisisha. .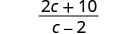
    Sababu ya kuangalia kwa sababu za kawaida. .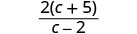
    Hakuna mambo ya kawaida; kujieleza kwa busara ni rahisi.  
    Mfano\(\PageIndex{32}\)

    Ondoa:\(\frac{2x+1}{x−7}−3\).

    Jibu

    \(\frac{−x+22}{x−7}\)

    Mfano\(\PageIndex{33}\)

    Ondoa:\(\frac{4y+3}{2y−1}−5\).

    Jibu

    \(\frac{−2(3y−4)}{2y−1}\)

    Ufafanuzi: Ongeza au Ondoa maneno ya busara.
    1. Kuamua kama maneno yana denominator ya kawaida.
      Ndiyo — nenda hatua ya 2.
      Hapana — Andika upya kila kujieleza mantiki na LCD.
      Kupata LCD.
      Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD.
    2. Ongeza au uondoe maneno ya busara.
    3. Kurahisisha, ikiwa inawezekana.

    Sisi kufuata hatua sawa na kabla ya kupata LCD wakati tuna maneno zaidi ya mbili busara. Katika mfano unaofuata tutaanza kwa kuzingatia madhehebu yote matatu ili kupata LCD yao.

    Mfano\(\PageIndex{34}\)

    Kurahisisha:\(\frac{2u}{u−1}+\frac{1}{u}−\frac{2u−1}{u^2−u}\).

    Jibu
      .
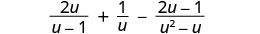
    Je! Maneno ya busara yana denominator ya kawaida? Hapana.  
    Kupata LCD. .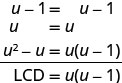  
    Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD. .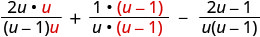
      .
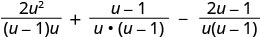
    Andika kama kujieleza moja ya busara. .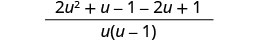
    Kurahisisha. .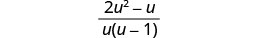
    Fanya namba, na uondoe mambo ya kawaida. .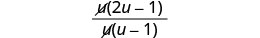
    Kurahisisha. .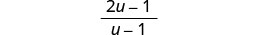
    Mfano\(\PageIndex{35}\)

    Kurahisisha:\(\frac{v}{v+1}+\frac{3}{v−1}−\frac{6}{v^2−1}\).

    Jibu

    \(\frac{v+3}{v+1}\)

    Mfano\(\PageIndex{36}\)

    Kuongeza mazoezi maandishi hapa.kurahisisha:\(\frac{3w}{w+2}+\frac{2}{w+7}−\frac{17w+4}{w^2+9w+14}\).

    Jibu

    \(\frac{3w}{w+7}\)

    Dhana muhimu

    • Pata Denominator ya kawaida ya maneno ya busara
      1. Factor kila kujieleza kabisa.
      2. Orodha ya mambo ya kila kujieleza. Mechi sababu wima ikiwezekana.
      3. Kuleta chini nguzo.
      4. Panua mambo.
    • Ongeza au Ondoa Maneno ya busara
      1. Kuamua kama maneno yana denominator ya kawaida.
        Ndiyo — nenda hatua ya 2.
        Hapana — Andika upya kila kujieleza mantiki na LCD.
        • Kupata LCD.
        • Andika upya kila kujieleza kwa busara kama kujieleza sawa na LCD.
      2. Ongeza au uondoe maneno ya busara.
      3. Kurahisisha, ikiwa inawezekana.