8.3E: Mazoezi
- Page ID
- 177724
Mazoezi hufanya kamili
Ongeza Maneno ya busara na Denominator ya kawaida
Katika mazoezi yafuatayo, ongeza.
\(\frac{2}{15}+\frac{7}{15}\)
- Jibu
-
\(\frac{3}{5}\)
\(\frac{4}{21}+\frac{3}{21}\)
\(\frac{7}{24}+\frac{11}{24}\)
- Jibu
-
\(\frac{3}{4}\)
\(\frac{7}{36}+\frac{13}{36}\)
\(\frac{3a}{a−b}+\frac{1}{a−b}\)
- Jibu
-
\(\frac{3a+1}{a-b}\)
\(\frac{3c}{4c−5}+\frac{5}{4c−5}\)
\(\frac{d}{d+8}+\frac{5}{d+8}\)
- Jibu
-
\(\frac{d+5}{d+8}\)
\(\frac{7m}{2m+n}+\frac{4}{2m+n}\)
\(\frac{p^2+10p}{p+2}+\frac{16}{p+2}\)
- Jibu
-
p+8
\(\frac{q^2+12q}{q+3}+\frac{27}{q+3}\)
\(\frac{2r^2}{2r−1}+\frac{15r−8}{2r−1}\)
- Jibu
-
r+8
\(\frac{3s^2}{3s−2}+\frac{13s−10}{3s−2}\)
\(\frac{8t^2}{t+4}+\frac{32t}{t+4}\)
- Jibu
-
8t
\(\frac{6v^2}{v+5}+\frac{30v}{v+5}\)
\(\frac{2w^2}{w^2−16}+\frac{8w}{w^2−16}\)
- Jibu
-
\(\frac{2w}{w−4}\)
\(\frac{7x^2}{x^2−9}+\frac{21x}{x^2−9}\)
Katika mazoezi yafuatayo, toa.
\(\frac{y^2}{y+8}−\frac{64}{y+8}\)
- Jibu
-
y-8
\(\frac{z^2}{z+2}−\frac{4}{z+2}\)
\(\frac{9a^2}{3a−7}−\frac{49}{3a−7}\)
- Jibu
-
3a+7
\(\frac{25b^2}{5b−6}−\frac{36}{5b−6}\)
\(\frac{c^2}{c−8}−\frac{6c+16}{c−8}\)
- Jibu
-
c+2
\(\frac{d^2}{d−9}−\frac{6d+27}{d−9}\)
\(\frac{3m^2}{6m−30}−\frac{21m−30}{6m−30}\)
- Jibu
-
\(\frac{m−2}{3}\)
\(\frac{2n^2}{4n−32}−\frac{30n−16}{4n−32}\)
\(\frac{6p^2+3p+4}{p^2+4p−5}−\frac{5p^2+p+7}{p^2+4p−5}\)
- Jibu
-
\(\frac{p+3}{p+5}\)
\(\frac{5q^2+3q−9}{q^2+6q+8}−\frac{4q^2+9q+7}{q^2+6q+8}\)
\(\frac{5r^2+7r−33}{r^2−49}−\frac{4r^2−5r−30}{r^2−49}\)
- Jibu
-
\(\frac{r+9}{r+7}\)
\(\frac{7t^2−t−4}{t^2−25}−\frac{6t^2+2t−1}{t^2−25}\)
Katika mazoezi yafuatayo, ongeza.
\(\frac{10v^2}{v−1}+\frac{2v+4}{1−2v}\)
- Jibu
-
4
\(\frac{20w}{5w−2}+\frac{5w+6}{2−5w}\)
\(\frac{10x^2+16x−7}{8x−3}+\frac{2x^2+3x−1}{3−8x}\)
- Jibu
-
x+2
\(\frac{6y^2+2y−11}{3y−7}+\frac{3y^2−3y+17}{7−3y}\)
Katika mazoezi yafuatayo, toa.
\(\frac{z^2+6z}{z^2−25}−\frac{3z+20}{25−z^2}\)
- Jibu
-
\(\frac{z+4}{z−5}\)
\(\frac{a^2+3a}{a^2−9}−\frac{3a−27}{9−a^2}\)
\(\frac{2b^2+30b−13}{b^2−49}−\frac{2b^2−5b−8}{49−b^2}\)
- Jibu
-
\(\frac{4b−3}{b−7}\)
\(\frac{c^2+5c−10}{c^2−16}−\frac{c^2−8c−10}{16−c^2}\)
kila siku Math
Sarah mbio 8 maili na kisha baiskeli 24 maili. Biking kasi yake ni 4 mph kasi zaidi kuliko kasi yake mbio. Ikiwa rr inawakilisha kasi ya Sarah wakati yeye mbio, basi muda wake wa kukimbia unatokana\(\frac{8}{r}\) na usemi na wakati wake wa kuendesha baiskeli unatokana na maneno\(\frac{24}{r+4}\). Kuongeza maneno mantiki ya kupata\(\frac{8}{r}+\frac{24}{r+4}\) kujieleza kwa jumla ya kiasi cha muda Sarah mbio na biked.
- Jibu
-
\(\frac{32r+32}{r(r+4)}\)
Ikiwa Pete anaweza kuchora ukuta katika masaa ya pp, basi kwa saa moja anaweza kuchora\(\frac{1}{p}\) ukuta. Itachukua Penelope masaa 3 zaidi kuliko Pete kuchora ukuta, hivyo saa moja anaweza kuchora\(\frac{1}{p+3}\) ukuta. Kuongeza maneno mantiki ya kupata\(\frac{1}{p}+\frac{1}{p+3}\) kujieleza kwa sehemu ya ukuta Pete na Penelope bila rangi katika saa moja kama kazi pamoja.
Mazoezi ya kuandika
Donald anadhani kuwa\(\frac{3}{x}+\frac{4}{x}\) ni\(\frac{7}{2x}\). Donald ni sahihi? Eleza.
Eleza jinsi unavyopata Denominator ya kawaida ya\(x^2+5x+4\) na\(x^2−16\).
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
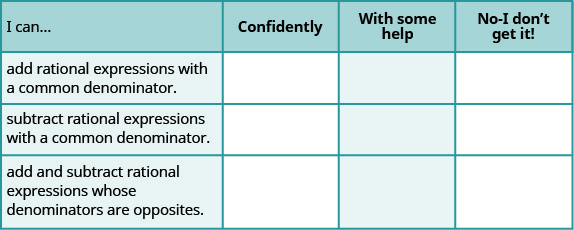
ⓑ Orodha hii inakuambia nini kuhusu ujuzi wako wa sehemu hii? Ni hatua gani utachukua ili kuboresha?


