Home
Kiswahili
Kitabu: Elementary Algebra (OpenStax)
8: Maneno ya busara na Ulinganisho
8.3: Ongeza na Ondoa Maneno ya busara na Denominator ya kawaida

8.3: Ongeza na Ondoa Maneno ya busara na Denominator ya kawaida

Last updated
Save as PDF

Page ID: 177711

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Ongeza maneno ya busara na denominator ya kawaida
Ondoa maneno ya busara na denominator ya kawaida
Ongeza na uondoe maneno ya busara ambao denominators ni kinyume

Kumbuka

Kabla ya kuanza, fanya jaribio hili la utayari.

Ikiwa umepoteza tatizo, rudi kwenye sehemu iliyoorodheshwa na uhakiki nyenzo.

Ongeza:$\frac{y}{3}+\frac{9}{3}$.
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.7.1.
Ondoa:$\frac{10}{x}−\frac{2}{x}$.
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.7.7.
Sababu kabisa:$8n^5−20n^3$.
Ikiwa umekosa tatizo hili, tathmini Zoezi 7.5.1.
Sababu kabisa:$45a^3−5ab^2$.
Ikiwa umekosa tatizo hili, tathmini Zoezi 7.5.10.

Ongeza Maneno ya busara na Denominator ya kawaida

Ni hatua gani ya kwanza unayochukua unapoongeza sehemu ndogo za namba? Unaangalia ikiwa wana denominator ya kawaida. Ikiwa wanafanya, unaongeza nambari na uweke jumla juu ya denominator ya kawaida. Ikiwa hawana denominator ya kawaida, unapata moja kabla ya kuongeza.

Ni sawa na maneno ya busara. Ili kuongeza maneno ya busara, lazima wawe na denominator ya kawaida. Wakati denominators ni sawa, unaongeza nambari na kuweka jumla juu ya denominator ya kawaida.

Ufafanuzi: MANTIKI EXPRESION

Ikiwa p, q, na r ni polynomials ambapo$r \ne 0$, basi

$\frac{p}{r}+\frac{q}{r}=\frac{p+q}{r}$

Ili kuongeza maneno ya busara na denominator ya kawaida, ongeza nambari na uweke jumla juu ya denominator ya kawaida.

Tutaongeza sehemu mbili za namba kwanza, kutukumbusha jinsi hii inafanyika.

Mfano$\PageIndex{1}$

Ongeza:$\frac{5}{18}+\frac{7}{18}$.

Jibu

	$\frac{5}{18}+\frac{7}{18}$
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	$\frac{5+7}{18}$
Ongeza kwenye nambari.	$\frac{12}{18}$
Factor nambari na denominator kuonyesha mambo ya kawaida.	$\frac{6·2}{6·3}$
Kurahisisha.	$\frac{2}{3}$

Mfano$\PageIndex{2}$

Ongeza:$\frac{7}{16}+\frac{5}{16}$.

Jibu: $\frac{3}{4}$

Mfano$\PageIndex{3}$

Ongeza:$\frac{3}{10}+\frac{1}{10}$.

Jibu: $\frac{2}{5}$

Kumbuka, hatuwezi kuruhusu maadili ambayo ingeweza kufanya denominator sifuri. Ni thamani gani ya yy inapaswa kutengwa katika mfano unaofuata?

Mfano$\PageIndex{4}$

Ongeza:$\frac{3y}{4y−3}+\frac{7}{4y−3}$.

Jibu

	$\frac{3y}{4y−3}+\frac{7}{4y−3}$.
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	$\frac{3y+7}{4y−3}$
Nambari na denominator haziwezi kuhesabiwa. Sehemu ni rahisi.

Mfano$\PageIndex{5}$

Ongeza:$\frac{5x}{2x+3}+\frac{2}{2x+3}$.

Jibu: $\frac{5x+2}{2x+3}$.

Mfano$\PageIndex{6}$

Ongeza:$\frac{x}{x−2}+\frac{1}{x−2}$.

Jibu: $\frac{x+1}{x−2}$

Mfano$\PageIndex{7}$

Ongeza:$\frac{7x+12}{x+3}+\frac{x^2}{x+3}$.

Jibu

	$\frac{7x+12}{x+3}+\frac{x^2}{x+3}$
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	$\frac{7x+12+x^2}{x+3}$
Andika digrii katika utaratibu wa kushuka.	$\frac{x^2+7x+12}{x+3}$
Fanya namba.	$\frac{(x+3)(x+4)}{x+3}$
Kurahisisha.	x+4

Mfano$\PageIndex{8}$

Ongeza:$\frac{9x+14}{x+7}+\frac{x^2}{x+7}$.

Jibu: x+2

Mfano$\PageIndex{9}$

Ongeza:$\frac{x^2+8x}{x+5}+\frac{15}{x+5}$.

Jibu: x+3

Ondoa Maneno ya busara na Denominator ya kawaida

Ili kuondoa maneno ya busara, lazima pia wawe na denominator ya kawaida. Wakati denominators ni sawa, wewe Ondoa nambari na kuweka tofauti juu ya denominator ya kawaida.

Ufafanuzi: MTAZAMO WA KUJIELEZA

Kama p, q, na r ni polynomials ambapo$r \ne 0$

$\frac{p}{r}−\frac{q}{r}=\frac{p−q}{r}$

Ili kuondoa maneno ya busara, toa nambari na uweke tofauti juu ya denominator ya kawaida.

Sisi daima kurahisisha maneno ya busara. Hakikisha kuzingatia, ikiwa inawezekana, baada ya kuondoa nambari ili uweze kutambua mambo yoyote ya kawaida.

Mfano$\PageIndex{10}$

Ondoa:$\frac{n^2}{n−10}−\frac{100}{n−10}$.

Jibu

	$\frac{n^2}{n−10}−\frac{100}{n−10}$
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	$\frac{n^2−100}{n−10}$
Fanya namba.	$\frac{(n−10)(n+10)}{n−10}$
Kurahisisha.	n+10

Mfano$\PageIndex{11}$

Ondoa:$\frac{x^2}{x+3}−\frac{9}{x+3}$.

Jibu: x-3

Mfano$\PageIndex{12}$

Ondoa:$\frac{4x^2}{2x−5}−\frac{25}{2x−5}$.

Jibu: 2x+5

Kuwa makini na ishara unapoondoa binomial!

Mfano$\PageIndex{13}$

Ondoa:$\frac{y^2}{y−6}−\frac{2y+24}{y−6}$.

Jibu

	$\frac{y^2}{y−6}−\frac{2y+24}{y−6}$
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	$\frac{y^2−(2y+24)}{y−6}$
Shirikisha ishara katika nambari.	$\frac{y^2−2y−24}{y−6}$
Fanya namba.	$\frac{(y−6)(y+4)}{y−6}$
Kurahisisha.	y+4

Mfano$\PageIndex{14}$

Ondoa:$\frac{n^2}{n−4}−\frac{n+12}{n−4}$.

Jibu: n+3

Mfano$\PageIndex{15}$

Ondoa:$\frac{y^2}{y−1}−\frac{9y−8}{y−1}$.

Jibu: y-8

Mfano$\PageIndex{16}$

Ondoa:$\frac{5x^2−7x+3}{x^2−3x-18}−\frac{4x^2+x−9}{x^2−3x-18}$.

Jibu

	$\frac{5x^2−7x+3}{x^2−3x+18}−\frac{4x^2+x−9}{x^2−3x+18}$
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	$\frac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18}$
Shirikisha ishara katika nambari.	$\frac{5x^2−7x+3−4x^2−x+9}{x^2−3x+18}$
Kuchanganya kama maneno.	$\frac{x^2−8x+12}{x^2−3x+18}$
Fanya namba na denominator.	$\frac{(x−2)(x−6)}{(x+3)(x−6)}$
Kurahisisha.	$\frac{x−2}{x+3}$

Mfano$\PageIndex{17}$

Ondoa:$\frac{4x^2−11x+8}{x^2−3x+2}−\frac{3x^2+x−3}{x^2−3x+2}$.

Jibu: $\frac{x−11}{x−2}$

Mfano$\PageIndex{18}$

Ondoa:$\frac{6x^2−x+20}{x^2−81}−\frac{5x^2+11x−7}{x^2−81}$.

Jibu: $\frac{x−3}{x+9}$

Ongeza na Ondoa Maneno ya Mantiki ambao Denominators ni kinyume

Wakati denominators ya maneno mawili ya busara ni kinyume, ni rahisi kupata denominator ya kawaida. Tunapaswa kuzidisha moja ya sehemu ndogo$\frac{−1}{−1}$

Hebu tuone jinsi hii inavyofanya kazi.

	$.$
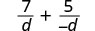Panua sehemu ya pili na$\frac{−1}{−1}$.	$.$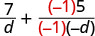
Denominators ni sawa.	$.$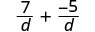
Kurahisisha.	$.$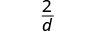

Mfano$\PageIndex{19}$

Ongeza:$\frac{4u−1}{3u−1}+\frac{u}{1−3u}$.

Jibu

	$.$
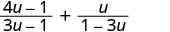
Panua sehemu ya pili na$\frac{−1}{−1}$.	$.$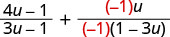
Kurahisisha sehemu ya pili.	$.$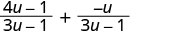
Denominators ni sawa. Ongeza nambari.	$.$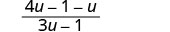
Kurahisisha.	$.$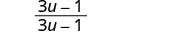
Kurahisisha.	$.$

Mfano$\PageIndex{20}$

Ongeza:$\frac{8x−15}{2x−5}+\frac{2x}{5−2x}$.

Jibu: 3

Mfano$\PageIndex{21}$

Ongeza:$\frac{6y^2+7y−10}{4y−7}+\frac{2y^2+2y+11}{7−4y}$.

Jibu: y+3

Mfano$\PageIndex{22}$

Ondoa:$\frac{m^2−6m}{m^2−1}−\frac{3m+2}{1−m^2}$.

Jibu

	$.$
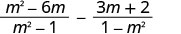
Panua sehemu ya pili na$\frac{−1}{−1}$.	$.$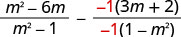
Kurahisisha sehemu ya pili.	$.$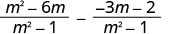
Denominators ni sawa. Ondoa nambari.	$.$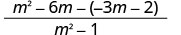
Kusambaza.	m2,16m+3m+2m2,11
Kuchanganya kama maneno.	$.$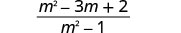
Fanya namba na denominator.	$.$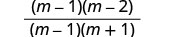
Kurahisisha kwa kuondoa mambo ya kawaida.	$.$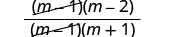
Kurahisisha.	$.$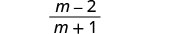

Mfano$\PageIndex{23}$

Ondoa:$\frac{y^2−5y}{y^2−4}−\frac{6y−6}{4−y^2}$.

Jibu: $\frac{y+3}{y+2}$

Mfano$\PageIndex{24}$

Ondoa:$\frac{2n^2+8n−1}{n^2−1}−\frac{n^2−7n−1}{1−n^2}$.

Jibu: $\frac{3n−2}{n−1}$

Dhana muhimu

Mantiki kujieleza Aidha
- Ikiwa p, q, na r ni polynomials ambapo$r \ne 0$, basi
  $\frac{p}{r}+\frac{q}{r}=\frac{p+q}{r}$
- Ili kuongeza maneno ya busara na denominator ya kawaida, ongeza nambari na uweke jumla juu ya denominator ya kawaida.
Mantiki kujieleza Ondoa
- Kama p, q, na r ni polynomials ambapo$r \ne 0$
  $\frac{p}{r}−\frac{q}{r}=\frac{p−q}{r}$
- Ili kuondoa maneno ya busara, toa nambari na uweke tofauti juu ya denominator ya kawaida.

	\(\frac{5}{18}+\frac{7}{18}\)
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	\(\frac{5+7}{18}\)
Ongeza kwenye nambari.	\(\frac{12}{18}\)
Factor nambari na denominator kuonyesha mambo ya kawaida.	\(\frac{6·2}{6·3}\)
Kurahisisha.	\(\frac{2}{3}\)

	\(\frac{5x^2−7x+3}{x^2−3x+18}−\frac{4x^2+x−9}{x^2−3x+18}\)
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	\(\frac{5x^2−7x+3−(4x^2+x−9)}{x^2−3x+18}\)
Shirikisha ishara katika nambari.	\(\frac{5x^2−7x+3−4x^2−x+9}{x^2−3x+18}\)
Kuchanganya kama maneno.	\(\frac{x^2−8x+12}{x^2−3x+18}\)
Fanya namba na denominator.	\(\frac{(x−2)(x−6)}{(x+3)(x−6)}\)
Kurahisisha.	\(\frac{x−2}{x+3}\)

Ufafanuzi: MANTIKI EXPRESION

Mfano\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\)

Mfano\(\PageIndex{7}\)

Mfano\(\PageIndex{8}\)

Mfano\(\PageIndex{9}\)

Ufafanuzi: MTAZAMO WA KUJIELEZA

Mfano\(\PageIndex{10}\)

Mfano\(\PageIndex{11}\)

Mfano\(\PageIndex{12}\)

Mfano\(\PageIndex{13}\)

Mfano\(\PageIndex{14}\)

Mfano\(\PageIndex{15}\)

Mfano\(\PageIndex{16}\)

Mfano\(\PageIndex{17}\)

Mfano\(\PageIndex{18}\)

Mfano\(\PageIndex{19}\)

Mfano\(\PageIndex{20}\)

Mfano\(\PageIndex{21}\)

Mfano\(\PageIndex{22}\)

Mfano\(\PageIndex{23}\)

Mfano\(\PageIndex{24}\)

	\(\frac{3y}{4y−3}+\frac{7}{4y−3}\).
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	\(\frac{3y+7}{4y−3}\)
Nambari na denominator haziwezi kuhesabiwa. Sehemu ni rahisi.

	\(\frac{7x+12}{x+3}+\frac{x^2}{x+3}\)
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	\(\frac{7x+12+x^2}{x+3}\)
Andika digrii katika utaratibu wa kushuka.	\(\frac{x^2+7x+12}{x+3}\)
Fanya namba.	\(\frac{(x+3)(x+4)}{x+3}\)
Kurahisisha.	x+4

	\(\frac{n^2}{n−10}−\frac{100}{n−10}\)
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	\(\frac{n^2−100}{n−10}\)
Fanya namba.	\(\frac{(n−10)(n+10)}{n−10}\)
Kurahisisha.	n+10

	\(\frac{y^2}{y−6}−\frac{2y+24}{y−6}\)
Sehemu ndogo zina denominator ya kawaida, hivyo ongeza nambari na uweke jumla juu ya denominator ya kawaida.	\(\frac{y^2−(2y+24)}{y−6}\)
Shirikisha ishara katika nambari.	\(\frac{y^2−2y−24}{y−6}\)
Fanya namba.	\(\frac{(y−6)(y+4)}{y−6}\)
Kurahisisha.	y+4

	$.$
Panua sehemu ya pili na\(\frac{−1}{−1}\).	$.$
Denominators ni sawa.	$.$
Kurahisisha.	$.$