Skip to main content
Global

8.5: Kurahisisha Maneno mazuri ya busara

  1. Last updated
  2. Save as PDF
  • Page ID
    177696

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kurahisisha tata kujieleza busara kwa kuandika kama mgawanyiko
    • Kurahisisha kujieleza kwa busara kwa kutumia LCD
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    Ikiwa umepoteza tatizo, rudi kwenye sehemu iliyoorodheshwa na uhakiki nyenzo.

    1. Kurahisisha:\(\frac{\frac{3}{5}}{\frac{9}{10}}\).
      Kama amekosa tatizo hili, kupitia Zoezi 1.6.25.
    2. Kurahisisha:\(\frac{1−\frac{1}{3}}{4^2+4·5}\).
      Kama amekosa tatizo hili, kupitia Zoezi 1.6.31.

    Sehemu ndogo ni sehemu ndogo ambazo namba au denominator ina sehemu. Katika Sura ya 1 sisi kilichorahisishwa sehemu tata kama hizi:

    \[\begin{array}{cc} {\frac{\frac{3}{4}}{\frac{5}{8}}}&{\frac{\frac{x}{2}}{\frac{xy}{6}}}\\ \nonumber \end{array}\]

    Katika sehemu hii tutawezesha maneno mazuri ya busara, ambayo ni maneno ya busara na maneno ya busara katika namba au denominator.

    Ufafanuzi: COMPLEX RATIONAL

    Maneno mazuri ya busara ni kujieleza kwa busara ambayo nambari au denominator ina kujieleza kwa busara.

    Hapa kuna maneno machache ya busara:

    \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\)

    \(\frac{\frac{2}{x+6}}{\frac{4}{x−6}−\frac{4}{x^2−36}}\)
    Kumbuka, sisi daima hutenganisha maadili ambayo ingeweza kufanya zero yoyote ya denominator.

    Tutatumia mbinu mbili ili kurahisisha maneno mazuri ya busara.

    Kurahisisha Complex Muhtasari kujieleza kwa kuandika kama Idara

    Tayari tumeona maneno haya mazuri ya busara mapema katika sura hii.

    \(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−8x+3}{x^2−5x+6}}\)

    Sisi alibainisha kuwa baa sehemu kutuambia kugawanya, hivyo rewrote kama tatizo mgawanyiko

    \((\frac{6x^2−7x+2}{4x−8})÷(\frac{2x^2−8x+3}{x^2−5x+6})\)

    Kisha tuliongeza maneno ya kwanza ya busara kwa usawa wa pili, kama tunavyofanya wakati tunagawanya sehemu mbili.

    Hii ni njia moja ya kurahisisha maneno ya busara. Tunaandika kama tulikuwa tukigawanya sehemu mbili.

    Mfano\(\PageIndex{1}\)

    \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\).

    Jibu
      \(\frac{\frac{4}{y−3}}{\frac{8}{y^2−9}}\)
    Andika upya sehemu tata kama mgawanyiko. \(\frac{4}{y−3}÷\frac{8}{y^2−9}\)
    Andika upya kama bidhaa ya mara ya kwanza ya kurudi kwa pili. \(\frac{4}{y−3}·\frac{y^2−9}{8}\)
    Kuzidisha. \(\frac{4(y^2−9)}{8(y−3)}\)
    Sababu ya kuangalia mambo ya kawaida. \(\frac{4(y−3)(y+3)}{8(y−3)}\)
    Kurahisisha. \(\frac{y+3}{2}\)

    Je, kuna thamani yoyote ya y ambayo haipaswi kuruhusiwa? Maneno rahisi ya busara yana tu mara kwa mara katika denominator. Lakini awali tata usemi wa busara ulikuwa na denominators ya y-3 na\(y^2−9\). Maneno haya yangekuwa yasiyofafanuliwa kama y=3 au y=—3

    Mfano\(\PageIndex{2}\)

    \(\frac{\frac{2}{x^2−1}}{\frac{3}{x+1}}\).

    Jibu

    \(\frac{2}{3(x−1)}\)

    Mfano\(\PageIndex{3}\)

    \(\frac{\frac{1}{x^2−7x+12}}{\frac{2}{x−4}}\).

    Jibu

    \(\frac{1}{2(x−3)}\)

    Mfano\(\PageIndex{4}\)

    \(\frac{\frac{1}{3}+\frac{1}{6}}{\frac{1}{2}−\frac{1}{3}}\).

    Jibu
      .
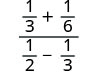
    Kurahisisha nambari na denominator.  
    Pata LCD na uongeze sehemu ndogo katika namba.
    Pata LCD na uongeze sehemu ndogo katika denominator.    		 .
    Kurahisisha nambari na denominator. .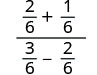
    Kurahisisha nambari na denominator, tena. .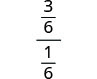
    Andika upya maneno mazuri ya busara kama tatizo la mgawanyiko. .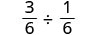
    Panua mara ya kwanza kwa usawa wa pili. .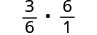
    Kurahisisha. .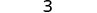
    Mfano\(\PageIndex{5}\)

    \(\frac{\frac{1}{2}+\frac{2}{3}}{\frac{5}{6}+\frac{1}{12}}\).

    Jibu

    \(\frac{14}{11}\)

    Mfano\(\PageIndex{6}\)

    \(\frac{\frac{3}{4}−\frac{1}{3}}{\frac{1}{8}+\frac{5}{6}}\).

    Jibu

    \(\frac{10}{23}\)

    Jinsi ya kurahisisha Ufafanuzi wa Kimantiki Tata kwa Kuandika kama Idara

    Mfano\(\PageIndex{7}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\).

    Jibu

    Picha hapo juu ina nguzo tatu. Picha inaonyesha hatua za jinsi ya kugawanya maneno mazuri ya busara katika hatua tatu. Hatua ya kwanza ni kurahisisha namba na denominator. Tutawezesha jumla katika nambari na tofauti katika denominator kwa mfano 1 imegawanywa na x plus 1 imegawanywa na y imegawanywa na x imegawanywa na y bala y kugawanywa na x Pata denominator ya kawaida na uongeze sehemu ndogo katika nambari. ili kupata mara 1 y kugawanywa na x mara y pamoja na mara 1 x kugawanywa na y mara x kugawanywa na x mara x kugawanywa na y mara x bala y mara y kugawanywa na x mara y Kisha, sisi kupata y kugawanywa na x y plus x pamoja x y kugawanywa na x y. nambari na moja katika denominator, y plus x imegawanywa na x y imegawanywa na x squared minus y squared imegawanywa na x y.Hatua mbili ni kuandika upya tata busara kujieleza kama tatizo mgawanyiko. Tunaandika namba iliyogawanywa na denominator.Hatua ya tatu ni kugawanya maneno. Panua kwanza kwa usawa wa pili ili kupata y plus x kugawanywa na x y mara x y kugawanywa na x squared minus y squared. Fanya maneno yoyote ikiwa inawezekana. Sasa tuna x y mara y pamoja x kugawanywa na x y mara x bala y mara x pamoja y Ondoa mambo ya kawaida. Msalaba x, y na y pamoja na x kutoka kwa nambari. Msalaba x, y na x pamoja na y kutoka kwa denominator. Kurahisisha kupata 1 kugawanywa na x minus y.

    Mfano\(\PageIndex{8}\)

    \(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{1}{x}−\frac{1}{y}}\).

    Jibu

    \(\frac{y+x}{y−x}\)

    Mfano\(\PageIndex{9}\)

    \(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{a^2}−\frac{1}{b^2}}\).

    Jibu

    \(\frac{ab}{b−a}\)

    Ufafanuzi: KURAHISISHA COMPLEX MANTIKI KUJIELEZA KWA KUANDIKA IT AS D
    1. Kurahisisha nambari na denominator.
    2. Andika upya maneno mazuri ya busara kama tatizo la mgawanyiko.
    3. Gawanya maneno.
    Mfano\(\PageIndex{10}\)

    \(\frac{n−\frac{4n}{n+5}}{\frac{1}{n+5}+\frac{1}{n−5}}\)

    Jibu
      .
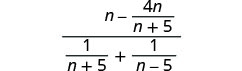
    Kurahisisha nambari na denominator.  
    Pata LCD na uongeze sehemu ndogo katika namba.
    Pata LCD na uongeze sehemu ndogo katika denominator.    		 .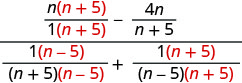
    Kurahisisha nambari. .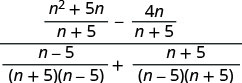

    Ondoa maneno ya busara katika nambari na uongeze kwenye denominator.    		 .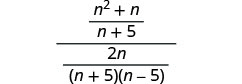
    Andika upya kama mgawanyiko wa sehemu. .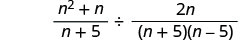
    Panua mara ya kwanza usawa wa pili. .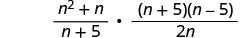
    Fanya maneno yoyote ikiwa inawezekana. .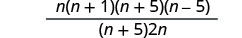
    Ondoa mambo ya kawaida. .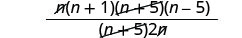
    Kurahisisha. .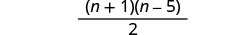
    Mfano\(\PageIndex{11}\)

    \(\frac{b−\frac{3b}{b+5}}{\frac{2}{b+5}+\frac{1}{b−5}}\).

    Jibu

    b (b+2)

    Mfano\(\PageIndex{12}\)

    \(\frac{1−\frac{3}{c+4}}{\frac{1}{c+4}+\frac{c}{3}}\).

    Jibu

    3c+3

    Kurahisisha Ufafanuzi wa busara tata kwa kutumia LCD

    Sisi “tulifuta” sehemu ndogo kwa kuzidisha na LCD wakati tulipotatua equations na sehemu ndogo. Tunaweza kutumia mkakati huo hapa ili kurahisisha maneno mazuri ya busara. Tutazidisha nambari na denominator na LCD ya maneno yote ya busara.

    Hebu tuangalie maneno mazuri ya busara tuliyorahisisha njia moja katika Mfano. Tutaifanya rahisi hapa kwa kuzidisha nambari na denominator na LCD. Wakati sisi kuzidisha na\(\frac{LCD}{LCD}\) sisi ni kuzidisha kwa 1, hivyo thamani anakaa sawa.

    Mfano\(\PageIndex{13}\)

    Kurahisisha:\(\frac{\frac{1}{3}+\frac{1}{6}}{\frac{1}{2}−\frac{1}{3}}\).

    Jibu
      .
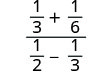
    LCD ya sehemu zote katika kujieleza nzima ni 6.  
    Futa sehemu ndogo kwa kuzidisha nambari na denominator kwa LCD hiyo. .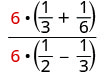
    Kusambaza. .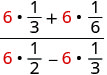
    Kurahisisha. .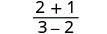
      .
      .
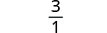
    Mfano\(\PageIndex{14}\)

    Kurahisisha:\(\frac{\frac{1}{2}+\frac{1}{5}}{\frac{1}{10}+\frac{1}{5}}\).

    Jibu

    \(\frac{7}{3}\)

    Mfano\(\PageIndex{15}\)

    Kurahisisha:\(\frac{\frac{1}{4}+\frac{3}{8}}{\frac{1}{2}−\frac{5}{16}}\).

    Jibu

    \(\frac{7}{3}\)

    Jinsi ya kurahisisha Ufafanuzi wa busara Tata kwa kutumia LCD

    Mfano\(\PageIndex{16}\)

    Kurahisisha:\(\frac{\frac{1}{x}+\frac{1}{y}}{\frac{x}{y}−\frac{y}{x}}\).

    Jibu

    Picha hapo juu ina nguzo 3. Inaonyesha hatua za jinsi ya kurahisisha kujieleza kwa busara tata kwa kutumia LCD kwa 1 imegawanywa na x plus 1 imegawanywa na y kugawanywa na y bala y kugawanywa na x Hatua ya kwanza ni kupata LCD ya sehemu zote katika kujieleza tata busara. LCD ya sehemu zote ni x y.Kuzidisha nambari na denominator na LCD.Hatua mbili ni kuzidisha namba zote mbili na denominator kwa x y ili kupata x y mara 1 imegawanywa na x plus 1 imegawanywa na y kugawanywa x mara y x imegawanywa na y minus y imegawanywa na x.Hatua ya tatu ni kurahisisha kujieleza. Kusambaza ili kupata x y mara 1 imegawanywa na x pamoja na x y mara 1 imegawanywa y kugawanywa na x y mara x imegawanywa na y minus x y mara y kugawanywa na x Kurahisisha kupata y plus x imegawanywa na x squared bala y squared. Ondoa mambo ya kawaida. Msalaba y pamoja na x katika nambari. Msalaba x pamoja na y katika nambari. Kurahisisha kupata 1 kugawanywa na x minus y.

    Mfano\(\PageIndex{17}\)

    Kurahisisha:\(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{a}{b}−\frac{b}{a}}\).

    Jibu

    \(\frac{b+a}{a^2+b^2}\)

    Mfano\(\PageIndex{18}\)

    Kurahisisha:\(\frac{\frac{1}{x^2}−\frac{1}{y^2}}{\frac{1}{x}−\frac{1}{y}}\).

    Jibu

    \(\frac{y−x}{xy}\)

    Ufafanuzi: KURAHISISHA COMPLEX MANTIKI KUJIELEZA KWA KUTUMIA LCD.
    1. Pata LCD ya vipande vyote katika kujieleza kwa busara.
    2. Panua nambari na denominator na LCD.
    3. Kurahisisha kujieleza.

    Hakikisha kuanza kwa kuzingatia madhehebu yote ili uweze kupata LCD.

    Mfano\(\PageIndex{19}\)

    Kurahisisha:\(\frac{\frac{2}{x+6}}{\frac{4}{x−6}−\frac{4}{x^2−36}}\).

    Jibu
      .
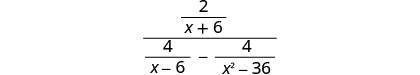
    Pata LCD ya vipande vyote katika kujieleza kwa busara. LCD ni (x+6) (x-6)  
    Panua nambari na denominator na LCD. .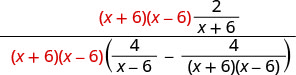
    Kurahisisha kujieleza.  
    Kusambaza katika denominator. .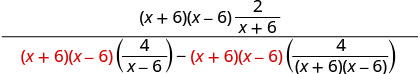
    Kurahisisha. .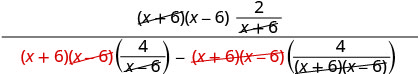
    Kurahisisha. .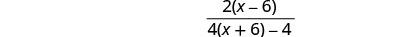
    Ili kurahisisha denominator, kusambaza na kuchanganya maneno kama hayo. .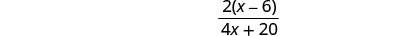
    Ondoa mambo ya kawaida. .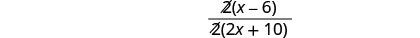
    Kurahisisha. .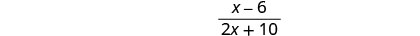
    Angalia kwamba hakuna mambo zaidi ya kawaida kwa nambari na denominator.  
    Mfano\(\PageIndex{20}\)

    Kurahisisha:\(\frac{\frac{3}{x+2}}{\frac{5}{x−2}−\frac{3}{x^2−4}}\).

    Jibu

    \(\frac{3x−6}{5x+7}\)

    Mfano\(\PageIndex{21}\)

    Kurahisisha:\(\frac{\frac{2}{x−7}−\frac{1}{x+7}}{\frac{6}{x+7}−\frac{1}{x^2−49}}\).

    Jibu

    \(\frac{x+21}{6x+43}\)

    Mfano\(\PageIndex{22}\)

    Kurahisisha:\(\frac{\frac{4}{m^2−7m+12}}{\frac{3}{m−3}−\frac{2}{m−4}}\).

    Jibu
      .
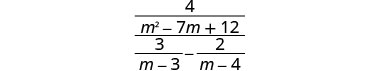
    Pata LCD ya vipande vyote katika kujieleza kwa busara. LCD ni (m-3) (m-4)  
    Panua nambari na denominator na LCD. .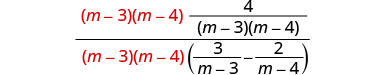
    Kurahisisha. .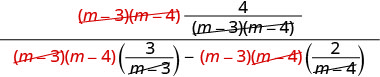
    Kurahisisha. .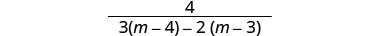
    Kusambaza. .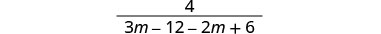
    Kuchanganya kama maneno. .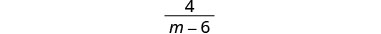
    Mfano\(\PageIndex{23}\)

    Kurahisisha:\(\frac{\frac{3}{x^2+7x+10}}{\frac{4}{x+2}+\frac{1}{x+5}}\).

    Jibu

    \(\frac{3}{5x+22}\)

    Mfano\(\PageIndex{24}\)

    Kurahisisha:\(\frac{\frac{4y}{y+5}+\frac{2}{y+6}}{\frac{3y}{y^2+11y+30}}\).

    Jibu

    \(\frac{6y+34}{3y}\)

    Mfano\(\PageIndex{25}\)

    Kurahisisha:\(\frac{\frac{y}{y+1}}{1+\frac{1}{y−1}}\).

    Jibu
      .
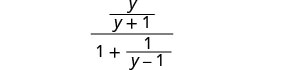
    Pata LCD ya vipande vyote katika kujieleza kwa busara.  
    LCD ni (y+1) (y-1)  
    Panua nambari na denominator na LCD. .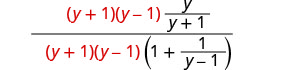
    Kusambaza katika denominator na kurahisisha. .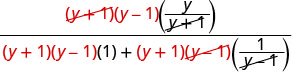
    Kurahisisha. .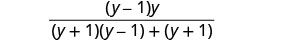
    Kurahisisha denominator, na uondoke namba ya hesabu. .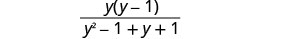
      .
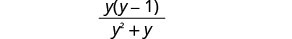
    Fanya denominator, na uondoe mambo ya kawaida na namba. .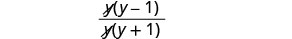
    Kurahisisha. .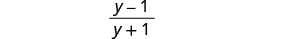
    Mfano\(\PageIndex{26}\)

    Kurahisisha:\(\frac{\frac{x}{x+3}}{1+\frac{1}{x+3}}\).

    Jibu

    \(\frac{x}{x+4}\)

    Mfano\(\PageIndex{27}\)

    Kurahisisha:\(\frac{1+\frac{1}{x−1}}{\frac{3}{x+1}}\).

    Jibu

    \(\frac{x(x+1)}{3(x−1)}\)

    Dhana muhimu

    • Kurahisisha kujieleza Mantiki kwa Kuandika kama Idara
      1. Kurahisisha nambari na denominator.
      2. Andika upya maneno mazuri ya busara kama tatizo la mgawanyiko.
      3. Gawanya maneno.
    • Kurahisisha Complex busara kujieleza kwa kutumia LCD
      1. Pata LCD ya vipande vyote katika kujieleza kwa busara.
      2. Panua nambari na denominator na LCD.
      3. Kurahisisha kujieleza.

    faharasa

    tata busara kujieleza
    Maneno mazuri ya busara ni kujieleza kwa busara ambayo nambari au denominator ina kujieleza kwa busara.