Skip to main content
Global

8.2: Panua na Gawanya Maneno ya busara

  1. Last updated
  2. Save as PDF
  • Page ID
    177737

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kuzidisha maneno ya busara
    • Gawanya maneno ya busara
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    Ikiwa umepoteza tatizo, rudi kwenye sehemu iliyoorodheshwa na uhakiki nyenzo.

    1. Kuzidisha:\(\frac{14}{15}·\frac{6}{35}\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 1.6.13.
    2. Gawanya:\(\frac{14}{15}÷\frac{6}{35}\).
      Kama amekosa tatizo hili, kupitia Zoezi 1.6.22.
    3. Sababu kabisa:\(2x^2−98\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 7.5.10.
    4. Sababu kabisa:\(10n^3+10\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 7.5.19.
    5. Sababu kabisa:\(10p^2−25pq−15q^2\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 7.5.28.

    Kuzidisha maneno ya busara

    Ili kuzidisha maneno ya busara, tunafanya tu kile tulichofanya na sehemu ndogo za namba. Sisi kuzidisha nambari na kuzidisha denominators. Kisha, ikiwa kuna mambo yoyote ya kawaida, tunawaondoa ili kurahisisha matokeo.

    Ufafanuzi: KUZIDISHA MANENO YA MANENO

    Ikiwa p, q, r, s ni polynomials wapi\(q \ne 0\) na\(s \ne 0\)

    \(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)

    Ili kuzidisha maneno ya busara, kuzidisha nambari na kuzidisha denominators.

    Tutafanya mfano wa kwanza na FRACTIONS namba kutukumbusha jinsi sisi tele FRACTIONS bila vigezo.

    Mfano\(\PageIndex{1}\)

    Kuzidisha:\(\frac{10}{28}·\frac{8}{15}\).

    Jibu
      .
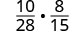
    Kuzidisha nambari na denominators. .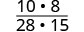
    Angalia mambo ya kawaida, na kisha uwaondoe. .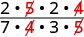
    Kurahisisha. .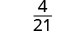
    Mfano\(\PageIndex{2}\)

    Kuzidisha:\(\frac{6}{10}·\frac{15}{12}\).

    Jibu

    \(\frac{3}{4}\)

    Mfano\(\PageIndex{3}\)

    Kuzidisha:\(\frac{20}{15}·\frac{6}{8}\).

    Jibu

    1

    Kumbuka, katika sura hii, tutafikiri kwamba maadili yote ya namba ambayo yangeweza kufanya denominator kuwa sifuri hutolewa. Hatuwezi kuandika vikwazo kwa kila kujieleza kwa busara, lakini kukumbuka kwamba denominator haiwezi kamwe kuwa sifuri. Hivyo katika mfano huu unaofuata,\(x \ne 0\) and \(y \ne 0\).

    Mfano\(\PageIndex{4}\)

    Kuzidisha:\(\frac{2x}{3y^2}·\frac{6xy^3}{x^{2}y}\).

    Jibu
      .
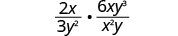
    Kuzidisha. .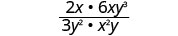
    Fanya namba na denominator kabisa, na kisha uondoe mambo ya kawaida. .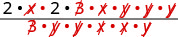
    Kurahisisha. .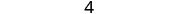
    Mfano\(\PageIndex{5}\)

    Kuzidisha:\(\frac{3pq}{q^2}·\frac{5p^{2}q}{6pq}\).

    Jibu

    \(\frac{5p^2}{2q}\)

    Mfano\(\PageIndex{6}\)

    Kuzidisha:\(\frac{6x^{3}y}{7x^2}·\frac{2xy}{3x^{2}y}\).

    Jibu

    \(\frac{12y^3}{7}\)

    Jinsi ya kuzidisha Maneno ya busara

    Mfano\(\PageIndex{7}\)

    Kuzidisha:\(\frac{2x}{x^2-7x+12}·\frac{x^2−9}{6x^2}\).

    Jibu

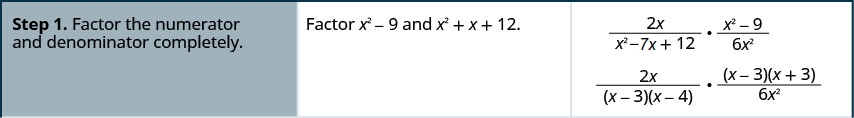
    Mfano 8.19.jpgHatua ya 2 ni kuzidisha nambari na denominators. Ni muhimu kuzidisha monomials kwanza. Kuzidisha mara 2x x minus mara 3 x pamoja 3 kugawanywa na 6x mara mraba x minus mara 3 x minus 4.Hatua ya 3 ni kugawanya mambo ya kawaida, kufuta 2, x, na x minus 3 katika namba na 2, x na x minus 3 katika denominator. Acha denominator katika fomu iliyopangwa ili kupata x pamoja na 3 imegawanywa na mara 3x x minus 4.

    Mfano\(\PageIndex{8}\)

    Kuzidisha:\(\frac{5x}{x^2+5x+6}·\frac{x^2−4}{10x}\).

    Jibu

    \(\frac{x−2}{2(x+3)}\)

    Mfano\(\PageIndex{9}\)

    Kuzidisha:\(\frac{9x^2}{x^2+11x+30}·\frac{x^2−36}{3x^2}\).

    Jibu

    \(\frac{3(x−6)}{x+5}\)

    Ufafanuzi: KUZIDISHA MAELEZO YA busara.
    1. Factor kila nambari na denominator kabisa.
    2. Kuzidisha nambari na denominators.
    3. Kurahisisha kwa kugawa mambo ya kawaida.
    Mfano\(\PageIndex{10}\)

    Kuzidisha:\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\).

    Jibu
      \(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\)
    Factor kila nambari na denominator. \(\frac{n(n−7)}{(n+1)(n+1)}·\frac{n+1}{2n}\)
    Kuzidisha nambari na denominators. \(\frac{n(n−7)(n+1)}{(n+1)(n+1)2n}\)
    Kurahisisha. \(\frac{n−7}{2(n+1)}\)
    Mfano\(\PageIndex{11}\)

    Kuzidisha:\(\frac{x^2−25}{x^2−3x−10}·\frac{x+2}{x}\).

    Jibu

    \(\frac{x+5}{x}\)

    Mfano\(\PageIndex{12}\)

    Kuzidisha:\(\frac{x^2−4x}{x^2+5x+6}·\frac{x+2}{x}\).

    Jibu

    \(\frac{x−4}{x+3}\)

    Mfano\(\PageIndex{13}\)

    Kuzidisha:\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\).

    Jibu
      \(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\)
    Factor kila nambari na denominator. \(\frac{4(4−x)}{2(x−6)}·\frac{(x−6)(x+1)}{(x−4)(x+4)}\)
    Kuzidisha nambari na denominators. \(\frac{4(4−x)(x−6)(x+1)}{2(x−6)(x−4)(x+4)}\)
    Kurahisisha. \(−\frac{2(x+1)}{(x+4)}\)
    Mfano\(\PageIndex{14}\)

    Kuzidisha:\(\frac{12x−6x^2}{x^2+8x}·\frac{x^2+11x+24}{x^2−4}\).

    Jibu

    \(−\frac{6(x+3)}{x+2}\)

    Mfano\(\PageIndex{15}\)

    Kuzidisha:\(\frac{9v−3v^2}{9v+36}·\frac{v^2+7v+12}{v^2−9}\).

    Jibu

    \(−\frac{v}{3}\)

    Mfano\(\PageIndex{16}\)

    Kuzidisha:\(\frac{2x−6}{x^2−8x+15}·\frac{x^2−25}{2x+10}\).

    Jibu
      .
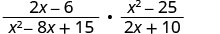
    Factor kila nambari na denominator. .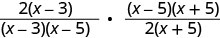
    Kuzidisha nambari na denominators. .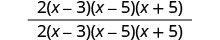
    Ondoa mambo ya kawaida. .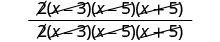
    Kurahisisha. .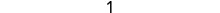
    Mfano\(\PageIndex{17}\)

    Kuzidisha:\(\frac{3a−21}{a^2−9a+14}·\frac{a^2−4}{3a+6}\).

    Jibu

    1

    Mfano\(\PageIndex{18}\)

    Kuzidisha:\(\frac{b^2−b}{b^2+9b−10}·\frac{b^2−100}{b^2−10b}\).

    Jibu

    1

    Gawanya Maneno ya busara

    Ili kugawanya maneno ya busara tunazidisha sehemu ya kwanza kwa usawa wa pili, kama tulivyofanya kwa sehemu ndogo za namba.

    Kumbuka, usawa wa\(\frac{a}{b}\) ni\(\frac{b}{a}\). Ili kupata usawa sisi tu kuweka nambari katika denominator na denominator katika nambari. Sisi “flip” sehemu.

    Ufafanuzi: MGAWANYIKO WA MANENO YA

    Ikiwa p, q, r, s ni polynomials ambapo\(q \ne 0\)\(r \ne 0\),\( s \ne 0\)

    \(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)

    Kugawanya maneno ya busara kuzidisha sehemu ya kwanza kwa usawa wa pili.

    Jinsi ya kugawanya Maneno ya busara

    Mfano\(\PageIndex{19}\)

    Gawanya:\(\frac{x+9}{6−x}÷\frac{x^2−81}{x−6}\).

    Jibu

    Picha hapo juu ina nguzo tatu. Inaonyesha hatua za kugawanya maneno ya busara. Hatua ya kwanza ni kuandika tena mgawanyiko kama bidhaa ya kujieleza kwa busara ya kwanza na usawa wa pili kwa x plus 9 imegawanywa na 6 minus x imegawanywa na x squared bala 81 imegawanywa na x minus 6. “Flip” sehemu ya pili na ubadili ishara ya mgawanyiko ili kuzidisha ili kupata x plus 9 imegawanywa na 6 minus x mara x minus 6 imegawanywa na x squared minus 81.Hatua mbili ni kuzingatia nambari na denominators kabisa. Factor x squared minus 81 kupata x pamoja 9 kugawanywa na 6 minus x mara x minus 6 kugawanywa na x minus mara 9 x pamoja 9.Hatua ya tatu ni kuzidisha nambari na denominators kupata x pamoja na mara 9 x minus 6 imegawanywa na 6 minus x mara x minus 9 mara x pamoja 9.Hatua ya nne ni kurahisisha kwa kugawa mambo ya kawaida. Gawanya mambo ya kawaida x pamoja na 9, x minus 6 kutoka kwa nambari na 6 minus x na x plus 9 kutoka kwa denominator. Kumbuka kupinga kugawanyika kwa hasi 1. Hii simplifies kwa hasi 1 kugawanywa na x minus 9.

    Mfano\(\PageIndex{20}\)

    Gawanya:\(\frac{c+3}{5−c}÷\frac{c^2−9}{c−5}\).

    Jibu

    \(−\frac{1}{c−3}\)

    Mfano\(\PageIndex{21}\)

    Gawanya:\(\frac{2−d}{d−4}÷\frac{4−d^2}{4−d}\).

    Jibu

    \(−\frac{1}{2+d}\)

    Ufafanuzi: GAWANYA MANENO YA MANENO.
    1. Andika upya mgawanyiko kama bidhaa ya kujieleza kwa busara ya kwanza na usawa wa pili.
    2. Factor numerators na denominators kabisa.
    3. Kuzidisha nambari na denominators pamoja.
    4. Kurahisisha kwa kugawa mambo ya kawaida.
    Mfano\(\PageIndex{22}\)

    Gawanya:\(\frac{3n^2}{n^2−4n}÷\frac{9n^2−45n}{n^2−7n+10}\).

    Jibu
      .
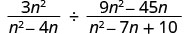
    Andika upya mgawanyiko kama bidhaa ya kujieleza kwa busara ya kwanza na usawa wa pili. .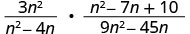
    Factor numerators na denominators na kisha kuzidisha. .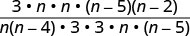
    Kurahisisha kwa kugawa mambo ya kawaida. .
      .
    Mfano\(\PageIndex{23}\)

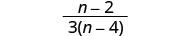
    Gawanya:\(\frac{2m^2}{m^2−8m}÷\frac{8m^2+24m}{m^2+m−6}\).

    Jibu

    \(\frac{(m−2)}{4(m−8)}\)

    Mfano\(\PageIndex{24}\)

    Gawanya:\(\frac{15n^2}{3n^2+33n}÷\frac{5n−5}{n^2+9n−22}\).

    Jibu

    \(\frac{n(n−2)}{n−1}\)

    Kumbuka, kwanza uandike tena mgawanyiko kama kuzidisha kwa kujieleza kwanza kwa usawa wa pili. Kisha fikiria kila kitu na uangalie mambo ya kawaida.

    Mfano\(\PageIndex{25}\)

    Gawanya:\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\).

    Jibu
      \(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\)
    Andika upya mgawanyiko kama bidhaa ya kujieleza kwa busara ya kwanza na usawa wa pili. \(\frac{2x^2+5x−12}{x^2−16}·\frac{x^2−8x+16}{2x^2−13x+15}\)
    Factor numerators na denominators na kisha kuzidisha. \(\frac{(2x−3)(x+4)(x−4)(x−4)}{(x−4)(x+4)(2x−3)(x−5)}\)
    Kurahisisha. \(\frac{(x−4)}{(x−5)}\)
    Mfano\(\PageIndex{26}\)

    Gawanya:\(\frac{3a^2−8a−3}{a^2−25}÷\frac{3a^2−14a−5}{a^2+10a+25}\).

    Jibu

    \(\frac{(a−3)(a+5)}{(a−5)(a−5)}\)

    Zoezi\(\PageIndex{27}\)

    Gawanya:\(\frac{4b^2+7b−2}{1−b^2}÷\frac{4b^2+15b−4}{b^2−2b+1}\).

    Jibu

    \(−\frac{(b+2)(b−1)}{(1+b)(b+4)}\)

    Mfano\(\PageIndex{28}\)

    Gawanya:\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\).

    Jibu
      \(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\)
    Andika upya mgawanyiko kama bidhaa ya kujieleza kwa busara ya kwanza na usawa wa pili. \(\frac{p^3+q^3}{2p^2+2pq+2q^2}·\frac{6}{p^2−q^2}\)
    Factor numerators na denominators na kisha kuzidisha. \(\frac{(p+q)(p^2−pq+q^2)6}{2(p^2+pq+q^2)(p−q)(p+q)}\)
    Kurahisisha. \(\frac{3(p^2−pq+q^2)}{(p−q)(p^2+pq+q^2)}\)
    Mfano\(\PageIndex{29}\)

    Gawanya:\(\frac{x^3−8}{3x^2−6x+12}÷\frac{x^2−4}{6}\).

    Jibu

    \(\frac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)

    Mfano\(\PageIndex{30}\)

    Gawanya:\(\frac{2z^2}{z^2−1}÷\frac{z^3−z^2+z}{z^3−1}\).

    Jibu

    \(\frac{2z(z^2+z+1)}{(z+1)(z^2−z+1)}\)

    Kabla ya kufanya mfano unaofuata, hebu tuangalie jinsi tunavyogawanya sehemu kwa idadi nzima. Wakati sisi kugawanya\(\frac{3}{5}÷4\)

    \[\begin{array}{c} {\frac{3}{5}÷4}\\ {\frac{3}{5}÷\frac{4}{1}}\\ {\frac{3}{5}·\frac{1}{4}}\\ \nonumber \end{array}\]

    Tunafanya kitu kimoja tunapogawanya maneno ya busara.

    Mfano\(\PageIndex{31}\)

    \(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\).

    Jibu
      \(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\)
    Andika maneno ya pili kama sehemu. \(\frac{a^2−b^2}{3ab}÷\frac{a^2+2ab+b^2}{1}\)
    Andika upya mgawanyiko kama mara ya kwanza ya kujieleza kwa usahihi wa kujieleza kwa pili. \(\frac{a^2−b^2}{3ab}·\frac{1}{a^2+2ab+b^2}\)
    Factor nambari na denominators, na kisha kuzidisha. \(\frac{(a−b)(a+b)1}{3ab·(a+b)(a+b)}\)
    Kurahisisha. \(\frac{a−b}{3ab(a+b)}\)
    Mfano\(\PageIndex{32}\)

    \(\frac{2x^2−14x−16}{4}÷(x2+2x+1)\).

    Jibu

    \(\frac{x−8}{2(x+1)}\)

    Mfano\(\PageIndex{33}\)

    \(\frac{y^2−6y+8}{y^2−4y}÷(3y2−12y)\).

    Jibu

    \(\frac{y−2}{3y(y−4)}\)

    Mfano\(\PageIndex{34}\)

    \(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\).

    Jibu
      \(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\)
    Andika upya na ishara ya mgawanyiko. \(\frac{6x^2−7x+2}{4x−8}÷\frac{2x^2−7x+3}{x^2−5x+6}\)
    Andika upya kama bidhaa ya mara ya kwanza ya usawa wa pili. \(\frac{6x^2−7x+2}{4x−8}·\frac{x^2−5x+6}{2x^2−7x+3}\)
    Factor numerators na denominators, na kisha kuzidisha \(\frac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)}\)
    Kurahisisha. \(\frac{3x−2}{4}\)
    Mfano\(\PageIndex{35}\)

    \(\frac{\frac{3x^2+7x+2}{4x+24}}{\frac{3x^2−14x−5}{x^2+x−30}}\).

    Jibu

    \(\frac{x+2}{4}\)

    Mfano\(\PageIndex{36}\)

    \(\frac{\frac{y^2−36}{2y^2+11y−6}}{\frac{2y^2−2y−60}{8y−4}}\).

    Jibu

    \(\frac{2}{y+5}\)

    Ikiwa tuna maneno zaidi ya mbili ya busara ya kufanya kazi na, bado tunafuata utaratibu huo. Hatua ya kwanza itakuwa kuandika tena mgawanyiko wowote kama kuzidisha kwa usawa. Kisha sisi sababu na kuzidisha.

    Mfano\(\PageIndex{37}\)

    \(\frac{3x−6}{4x−4}·\frac{x^2+2x−3}{x^2−3x−10}÷\frac{2x+12}{8x+16}\).

    Jibu
      .
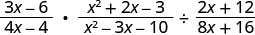
    Andika upya mgawanyiko kama kuzidisha kwa usawa. .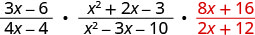
    Factor nambari na denominators, na kisha kuzidisha. .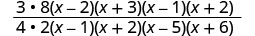
    Kurahisisha kwa kugawa mambo ya kawaida. .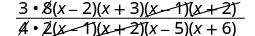
    Kurahisisha. .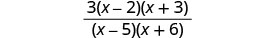
    Mfano\(\PageIndex{38}\)

    \(\frac{4m+4}{3m−15}·\frac{m^2−3m−10}{m^2−4m−32}÷\frac{12m−36}{6m−48}\).

    Jibu

    \(\frac{2(m+1)(m+2)}{3(m+4)(m−3)}\)

    Mfano\(\PageIndex{39}\)

    \(\frac{2n^2+10n}{n−1}÷\frac{n^2+10n+24}{n^2+8n−9}·\frac{n+4}{8n^2+12n}\).

    Jibu

    \(\frac{(n+5)(n+9)}{2(n+6)(2n+3)}\)

    Dhana muhimu

    • Kuzidisha kwa Maneno ya busara
      • Ikiwa p, q, r, s ni polynomials wapi\(q \ne 0\) na\(s \ne 0\), basi\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)
      • Ili kuzidisha maneno ya busara, kuzidisha nambari na kuzidisha denominators
    • Kuzidisha kujieleza kwa busara
      1. Factor kila nambari na denominator kabisa.
      2. Kuzidisha nambari na denominators.
      3. Kurahisisha kwa kugawa mambo ya kawaida.
    • Idara ya Maneno ya busara
      • Ikiwa p, q, r, s ni polynomials ambapo\(q \ne 0\),\(r \ne 0\),\( s \ne 0\), basi\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
      • Kugawanya maneno ya busara kuzidisha sehemu ya kwanza kwa usawa wa pili.
    • Gawanya Maneno ya busara
      1. Andika upya mgawanyiko kama bidhaa ya kujieleza kwa busara ya kwanza na usawa wa pili.
      2. Factor numerators na denominators kabisa.
      3. Kuzidisha nambari na denominators pamoja.
      4. Kurahisisha kwa kugawa mambo ya kawaida.