8.1E: Mazoezi
- Page ID
- 177735
Mazoezi hufanya kamili
Katika mazoezi yafuatayo, tambua maadili ambayo maneno ya busara hayajafafanuliwa.
- \(\dfrac{2x}{z}\)
- \(\dfrac{4p−1}{6p−5}\)
- \(\dfrac{n−3}{n^2+2n−8}\)
- Jibu
-
- z=0
- \(p=\dfrac{5}{6}\)
- n=-4, n=2
- \(\dfrac{10m}{11n}\)
- \(\dfrac{6y+13}{4y−9}\)
- \(\dfrac{b−8}{b^2−36}\)
- \(\dfrac{4x^{2}y}{3y}\)
- \(\dfrac{3x−2}{2x+1}\)
- \(\dfrac{u−1}{u^2−3u−28}\)
- Jibu
-
- y=0
- \(x=−\dfrac{1}{2}\)
- u=-4, u=7
- \(\dfrac{5pq^{2}}{9q}\)
- \(\dfrac{7a−4}{3a+5}\)
- \(\dfrac{1}{x^2−4}\)
Tathmini Maneno ya busara
Katika mazoezi yafuatayo, tathmini ya kujieleza kwa busara kwa maadili yaliyotolewa.
\(\dfrac{2x}{x−1}\)
- x=0
- x=2
- x=-1
- Jibu
-
- 0
- 4
- 1
\(\dfrac{4y−1}{5y−3}\)
- y=0
- y=2
- y=-1
\(\dfrac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=-2
- Jibu
-
- 3
- \(\dfrac{5}{2}\)
- \(−\dfrac{1}{5}\)
\(\dfrac{x+3}{2−3x}\)
- x=0
- x=1
- x=-1
\(\dfrac{y^2+5y+6}{y^2−1}\)
- y=0
- y=2
- y=-1
- Jibu
-
- -6
- \(\dfrac{20}{3}\)
- 0
\(\dfrac{z^2+3z−10}{z^2−1}\)
- z=0
- z=2
- z=-2
\(\dfrac{a^2−4}{a^2+5a+4}\)
- a=0
- a=1
- a=-2
- Jibu
-
- -1
- \(−\dfrac{3}{10}\)
- 0
\(\dfrac{b^2+2}{b^2−3b−4}\)
- b=0
- b=2
- b=-1
\(\dfrac{x^2+3xy+2y^2}{2x^{3}y}\)
- x=1, y=-1
- x=2, y=1
- x=-1, y=-1
- Jibu
-
- 0
- \(\dfrac{3}{4}\)
- \(\dfrac{15}{4}\)
\(\dfrac{c^2+cd−2d^2}{cd^{3}}\)
- c=2, d=-1
- c=1, d=-1
- c=-1, d=2
\(\dfrac{m^2−4n^2}{5mn^3}\)
- m=2, n=1
- m=-1, n=-1
- m=3, n=2
- Jibu
-
- 0
- \(−\dfrac{3}{5}\)
- \(−\dfrac{7}{20}\)
\(\dfrac{2s^{2}t}{s^2−9t^2}\)
- s=4, t=1
- s=-1, t=-1
- s=0, t=2
Kurahisisha maneno ya busara
Katika mazoezi yafuatayo, kurahisisha.
\(−\dfrac{4}{52}\)
- Jibu
-
\(−\dfrac{1}{13}\)
\(−\dfrac{44}{55}\)
\(\dfrac{56}{63}\)
- Jibu
-
\(\dfrac{8}{9}\)
\(\dfrac{65}{104}\)
\(\dfrac{6ab^{2}}{12a^{2}b}\)
- Jibu
-
\(\dfrac{b}{2a}\)
\(\dfrac{15xy^{3}}{x^{3}y^{3}}\)
\(\dfrac{8m^{3}n}{12mn^2}\)
- Jibu
-
\(\dfrac{2m^2}{3n}\)
\(\dfrac{36v^{3}w^2}{27vw^3}\)
\(\dfrac{3a+6}{4a+8}\)
- Jibu
-
\(\dfrac{3}{4}\)
\(\dfrac{5b+5}{6b+6}\)
\(\dfrac{3c−9}{5c−15}\)
- Jibu
-
\(\dfrac{3}{5}\)
\(\dfrac{4d+8}{9d+18}\)
\(\dfrac{7m+63}{5m+45}\)
- Jibu
-
\(\dfrac{7}{5}\)
\(\dfrac{8n−96}{3n−36}\)
\(\dfrac{12p−240}{5p−100}\)
- Jibu
-
\(\dfrac{12}{5}\)
\(\dfrac{6q+210}{5q+175}\)
\(\dfrac{a^2−a−12}{a^2−8a+16}\)
- Jibu
-
\(\dfrac{a+3}{a−4}\)
\(\dfrac{x^2+4x−5}{x^2−2x+1}\)
\(\dfrac{y^2+3y−4}{y^2−6y+5}\)
- Jibu
-
\(\dfrac{y+4}{y−5}\)
\(\dfrac{v^2+8v+15}{v^2−v−12}\)
\(\dfrac{x^2−25}{x^2+2x−15}\)
- Jibu
-
\(\dfrac{x−5}{x−3}\)
\(\dfrac{a^2−4}{a^2+6a−16}\)
\(\dfrac{y^2−2y−3}{y^2−9}\)
- Jibu
-
\(\dfrac{y+1}{y+3}\)
\(\dfrac{b^2+9b+18}{b^2−36}\)
\(\dfrac{y^3+y^2+y+1}{y^2+2y+1}\)
- Jibu
-
\(\dfrac{y^2+1}{y+1}\)
\(\dfrac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\dfrac{x^3−2x^2−25x+50}{x^2−25}\)
- Jibu
-
x-2
\(\dfrac{q^3+3q^2−4q−12}{q^2−4}\)
\(\dfrac{3a^2+15a}{6a^2+6a−36}\)
- Jibu
-
\(\dfrac{a(a+5)}{2(a+3)(a−2)}\)
\(\dfrac{8b^2−32b}{2b^2−6b−80}\)
\(\dfrac{−5c^2−10c}{−10c^2+30c+100}\)
- Jibu
-
\(\dfrac{c}{2(c−5)}\)
\(\dfrac{4d^2−24d}{2d^2−4d−48}\)
\(\dfrac{3m^2+30m+75}{4m^2−100}\)
- Jibu
-
\(\dfrac{3(m+5)}{4(m−5)}\)
\(\dfrac{5n^2+30n+45}{2n^2−18}\)
\(\dfrac{5r^2+30r−35}{r^2−49}\)
- Jibu
-
\(\dfrac{5(r−1)}{r+7}\)
\(\dfrac{3s^2+30s+72}{3s^2−48}\)
\(\dfrac{t^3−27}{t^2−9}\)
- Jibu
-
\(\dfrac{t^2+3t+9}{t+3}\)
\(\dfrac{v^3−1}{v^2−1}\)
\(\dfrac{w^3+216}{w^2−36}\)
- Jibu
-
\(\dfrac{w^2−6w+36}{w−6}\)
\(\dfrac{v^3+125}{v^2−25}\)
Kurahisisha maneno ya busara na Mambo ya kinyume
Katika mazoezi yafuatayo, kurahisisha kila kujieleza kwa busara.
\(\dfrac{a−5}{5−a}\)
- Jibu
-
-1
\(\dfrac{b−12}{12−b}\)
\(\dfrac{11−c}{c−11}\)
- Jibu
-
-1
\(\dfrac{5−d}{d−5}\)
\(\dfrac{12−2x}{x^2−36}\)
- Jibu
-
\(−\dfrac{2}{x+6}\)
\(\dfrac{20−5y}{y^2−16}\)
\(\dfrac{4v−32}{64−v^2}\)
- Jibu
-
\(−\dfrac{4}{8+v}\)
\(\dfrac{7w−21}{9−w^2}\)
\(\dfrac{y^2−11y+24}{9−y^2}\)
- Jibu
-
\(−\dfrac{y−8}{3+y}\)
\(\dfrac{z^2−9z+20}{16−z^2}\)
\(\dfrac{a^2−5a−36}{81−a^2}\)
- Jibu
-
\(−\dfrac{a+4}{9+a}\)
\(\dfrac{b^2+b−42}{36−b^2}\)
kila siku Math
Viwango vya Kodi Kwa mwaka wa kodi 2015, kiasi cha kodi inadaiwa na mtu mmoja anayepata kati ya $37,450 na $90,750, kinaweza kupatikana kwa kutathmini formula 0.25x-4206.25, ambapo x ni mapato. Kiwango cha wastani cha kodi kwa mapato haya kinaweza kupatikana kwa kutathmini formula\(\dfrac{0.25x−4206.25}{x}\). Je! Kiwango cha wastani cha kodi kwa mtu mmoja anayepata $50,000?
- Jibu
-
16.5%
Kazi urefu wa muda inachukua kwa watu wawili kwa kufanya kazi sawa kama kazi pamoja inaweza kupatikana kwa kutathmini formula\(\dfrac{xy}{x+y}\). Kama Tom anaweza kuchora tundu katika x=45 dakika na ndugu yake Bobby anaweza kuipaka katika y=dakika 60, itachukua dakika ngapi ikiwa wanafanya kazi pamoja?
Mazoezi ya kuandika
Eleza jinsi unavyopata maadili ya x ambayo kujieleza kwa busara\(\dfrac{x^2−x−20}{x^2−4}\) haijulikani.
- Jibu
-
Majibu yatatofautiana, lakini wote wanapaswa kutaja kuweka kazi ya denominator kwa sifuri.
Eleza hatua zote unazochukua ili kurahisisha kujieleza kwa busara\(\dfrac{p^2+4p−21}{9−p^2}\).
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
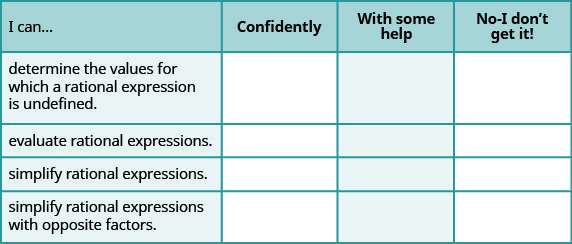
ⓑ Kama wengi wa hundi yako walikuwa:
... kwa ujasiri. Hongera! Umefanikiwa malengo yako katika sehemu hii! Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum!
... kwa msaada fulani. Hii lazima kushughulikiwa haraka kama mada huna bwana kuwa mashimo katika barabara yako ya mafanikio. Math ni mtiririko - kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?
... hapana - Siipati! Hii ni muhimu na haipaswi kupuuza. Unahitaji kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo ili kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.


