8.1: Kurahisisha Maneno ya busara
- Page ID
- 177723
Mwishoni mwa sehemu hii, utaweza:
- Kuamua maadili ambayo kujieleza kwa busara haijulikani
- Tathmini maneno ya busara
- Kurahisisha maneno ya busara
- Kurahisisha maneno ya busara na mambo tofauti
Kabla ya kuanza, fanya jaribio hili la utayari.
Ikiwa umepoteza tatizo, rudi kwenye sehemu iliyoorodheshwa na uhakiki nyenzo.
Katika Sura ya 1, tulipitia upya mali ya sehemu ndogo na shughuli zao. Tulianzisha namba za busara, ambazo ni sehemu ndogo tu ambapo nambari na denominators ni integers, na denominator sio sifuri.
Katika sura hii, tutafanya kazi na sehemu ambazo nambari na denominators ni polynomials. Tunaita maneno haya ya busara.
Maneno ya busara ni usemi wa fomu\(\frac{p(x)}{q(x)}\), ambapo p na q ni polynomials na\(q \ne 0\).
Hapa ni baadhi ya mifano ya maneno ya busara:
\[\begin{array}{cccc} {−\frac{13}{42}}&{\frac{7y}{8z}}&{\frac{5x+2}{x^2−7}}&{\frac{4x^2+3x−1}{2x−8}}\\ \nonumber \end{array}\]
Kumbuka kwamba kwanza busara kujieleza waliotajwa hapo juu\(−\frac{13}{42}\),, ni sehemu tu. Kwa kuwa mara kwa mara ni polynomial na sifuri shahada, uwiano wa mara kwa mara mbili ni kujieleza kwa busara, ikiwa ni pamoja na denominator si sifuri.
Tutafanya shughuli sawa na maneno ya busara ambayo tunafanya na sehemu ndogo. Sisi kurahisisha, kuongeza, Ondoa, kuzidisha, kugawanya, na kuitumia katika programu.
Tambua Maadili ambayo Ufafanuzi wa busara haukufafanuliwa
Tunapofanya kazi na sehemu ya namba, ni rahisi kuepuka kugawa kwa sifuri, kwa sababu tunaweza kuona namba katika denominator. Ili kuepuka kugawa kwa sifuri kwa kujieleza kwa busara, hatupaswi kuruhusu maadili ya kutofautiana ambayo itafanya denominator kuwa sifuri.
Ikiwa denominator ni sifuri, kujieleza kwa busara haijulikani. Nambari ya kujieleza kwa busara inaweza kuwa 0—lakini sio denominator.
Hivyo kabla ya kuanza operesheni yoyote na kujieleza mantiki, sisi kuchunguza ni kwanza kupata maadili ambayo kufanya denominator sifuri. Kwa njia hiyo, tunapotatua usawa wa busara kwa mfano, tutajua kama ufumbuzi wa algebraic tunayopata unaruhusiwa au la.
- Weka denominator sawa na sifuri.
- Tatua equation katika seti ya reals, ikiwa inawezekana.
Kuamua maadili ambayo kujieleza kwa busara haijulikani:
- \(\frac{9y}{x}\)
- \(\frac{4b−3}{2b+5}\)
- \(\frac{x+4}{x^2+5x+6x}\)
Suluhisho
Maneno hayatakuwa na ufafanuzi wakati denominator ni sifuri.
| 1. | \(\frac{9y}{x}\) |
| Weka denominator sawa na sifuri. Tatua kwa kutofautiana. | x=0 |
| \(\frac{9y}{x}\)haijafafanuliwa kwa x=0. | |
| 2. |
\(\frac{4b−3}{2b+5}\) |
| Weka denominator sawa na sifuri. Tatua kwa kutofautiana. | 2b+5=0 |
| 2b=-5 | |
| \(b=−\frac{5}{2}\) | |
| \(\frac{4b−3}{2b+5}\)haijafafanuliwa kwa\(b=−\frac{5}{2}\). | |
| 3. | \(\frac{x+4}{x^2+5x+6x}\) |
| Weka denominator sawa na sifuri. Tatua kwa kutofautiana. | \(x^2+5x+6x=0\) |
| \((x+2)(x+3)=0\) | |
| x+2=0 au x+3=0 | |
| x=-2 au x=-3 | |
| \(\frac{x+4}{x^2+5x+6x}\)haijafafanuliwa kwa x=-1 au x=—3. |
Kusema kuwa\(\frac{x+4}{x^2+5x+6x}\) usemi wa busara haujafafanuliwa kwa x=—2aorx=1-3 ni sawa na kuandika maneno “batili ambapo marufuku” katika sheria za mashindano.
Jaribu\(\PageIndex{2}\)
Kuamua maadili ambayo kujieleza kwa busara haijulikani:
- \(\frac{3y}{x}\)
- \(\frac{8n−5}{3n+1}\)
- \(\frac{a+10}{a^2+4a+3a}\)
- Answer
-
- x=0
- \(n=−\frac{1}{3}\)
- a=−1, a=−3
Try It \(\PageIndex{3}\)
Kuamua maadili ambayo kujieleza kwa busara haijulikani:
- \(\frac{4p}{5q}\)
- \(\frac{y−1}{3y+2}\)
- \(\frac{m−5}{m^2+m−6}\)
- Jibu
-
- q=0
- \(y=−\frac{2}{3}\)
- m=2, m=-3
Tathmini Maneno ya busara
Kutathmini kujieleza mantiki, sisi badala maadili ya vigezo katika kujieleza na kurahisisha, kama sisi kwa maneno mengine mengi katika kitabu hiki.
Tathmini\(\frac{2x+3}{3x−5}\) kwa kila thamani:
- x=0
- x=2
- x=-3
Suluhisho
| 1. |  |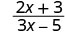
 |
 |
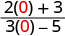| Kurahisisha. |  |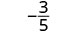
| 2. |  |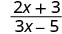
 |
 |
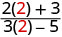| Kurahisisha. |  |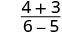
 |
|
 |
|
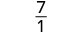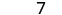| 3. |  |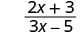
 |
 |
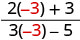| Kurahisisha. |  |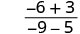
 |
|
 |
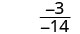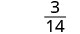Jaribu\(\PageIndex{5}\)
Tathmini\(\frac{y+1}{2y−3}\) for each value:
- y=1
- y=−3
- y=0
- Answer
-
- −2
- \(\frac{2}{9}\)
- \(−\frac{1}{3}\)
Try It \(\PageIndex{6}\)
Tathmini\(\frac{5x−1}{2x+1}\) kwa kila thamani:
- x=1
- x=-1
- x=0
- Jibu
-
- \(\frac{4}{3}\)
- 6
- -1
Tathmini\(\frac{x^2+8x+7}{x^2−4}\) kwa kila thamani:
- x=0
- x=2
- x=-1
Suluhisho
| 1. |  |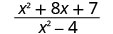
 |
 |
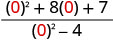| Kurahisisha. |  |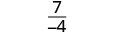
 |
|
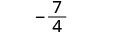| 2. | |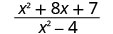
 |
 |
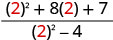| Kurahisisha. |  |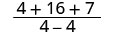
 |
|
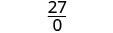| Maneno haya ya busara haijulikani kwa x = 2. | |
| 3. |  |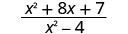
 |
 |
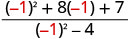| Kurahisisha. |  |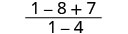
 |
|
 |
|
 |
|
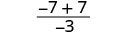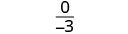Jaribu\(\PageIndex{8}\)
Tathmini\(\frac{x^2+1}{x^2−3x+2}\) for each value:
- x=0
- x=−1
- x=3
- Answer
-
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- 2
Try It \(\PageIndex{9}\)
Tathmini\(\frac{x^2+x−6}{x^2−9}\) kwa kila thamani.
- x=0
- x=-1
- x=1
- Jibu
-
- \(\frac{2}{3}\)
- \(\frac{4}{5}\)
- \(\frac{1}{2}\)
Kumbuka kwamba sehemu ni rahisi wakati haina mambo ya kawaida, isipokuwa 1, katika nambari yake na denominator. Tunapotathmini kujieleza kwa busara, tunahakikisha kurahisisha sehemu inayosababisha.
Tathmini\(\frac{a^2+2ab+b^2}{3ab}\) kwa kila thamani.
- a=1, b=2
- a=-2, b=-1
- \(a=\frac{1}{3}\), b=0
Suluhisho
| 1. | \(\frac{a^2+2ab+b^2}{3ab}\)wakati a=1, b=2 |
 |
 |
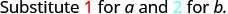| Kurahisisha. |  |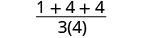
 |
|
 |
|
| 2. | \(\frac{a^2+2ab+b^2}{3ab}\)wakati a=-1, b=-1 |
 |
 |
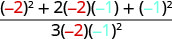| Kurahisisha. |  |
 |
|
 |
|
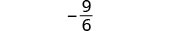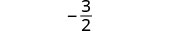| 3. | \(\frac{a^2+2ab+b^2}{3ab}\)wakati\(a=\frac{1}{3}\), b=0 |
 |
 |
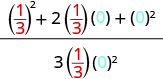| Kurahisisha. |  |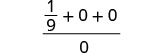
 |
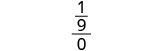Jaribu\(\PageIndex{11}\)
Tathmini\(\frac{2a^{3}b}{a^2+2ab+b^2}\) for each value.
- a=−1, b=2
- a=0, b=−1
- a=1, \(b=\frac{1}{2}\)
- Answer
-
- −4
- 0
- \(\frac{4}{9}\)
Try It \(\PageIndex{12}\)
Tathmini\(\frac{a^2−b^2}{8ab^3}\) kwa kila thamani:
- a=1, b=-1
- \(a=\frac{1}{2}\), b=-1
- a=-1, b=1
- Jibu
-
- 0
- \(\frac{3}{16}\)
- \(\frac{3}{16}\)
Kurahisisha maneno ya busara
Kama vile sehemu inachukuliwa kuwa rahisi ikiwa hakuna sababu za kawaida, isipokuwa 1, katika nambari yake na denominator, kujieleza kwa busara ni rahisi ikiwa haina mambo ya kawaida, isipokuwa 1, katika nambari yake na denominator.
Maneno ya busara yanachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida katika nambari yake na denominator.
Kwa mfano:
- \(\frac{2}{3}\)ni rahisi kwa sababu hakuna sababu ya kawaida ya 2 na 3.
- \(\frac{2x}{3x}\)si rahisi kwa sababu x ni sababu ya kawaida ya 2 x na 3 x.
Tunatumia Mali sawa FRACTIONS ili kurahisisha sehemu ndogo za namba. Sisi restate hapa kama sisi pia kutumia ili kurahisisha mantiki kujieleza s.
Ikiwa a, b, na c ni namba ambapo\(b \ne 0\),\(c\ne 0\), basi\(\frac{a}{b}=\frac{a·c}{b·c}\) na\(\frac{a·c}{b·c}=\frac{a}{b}\)
Ona kwamba katika Mali sawa Fractions, maadili ambayo ingeweza kufanya denominators sifuri ni hasa haruhusiwi. Tunaona\(b \ne 0\),\(c\ne 0\) wazi. Kila wakati sisi kuandika kujieleza busara, tunapaswa kufanya kauli sawa disallowing maadili ambayo kufanya denominator sifuri. Hata hivyo, ili tuangalie kazi iliyopo, tutaacha kuandika katika mifano.
Hebu tuanze kwa kuchunguza jinsi tunavyorahisisha sehemu ndogo za namba.
Kurahisisha:\(−\frac{36}{63}\).
Suluhisho
 |
|
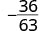| Andika upya nambari na denominator kuonyesha mambo ya kawaida. |  |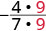
| Kurahisisha kutumia sawa FRACTIONS Mali. |  |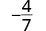
Angalia kwamba sehemu\(−\frac{4}{7}\) ni rahisi kwa sababu hakuna mambo ya kawaida zaidi.
Jaribu\(\PageIndex{14}\)
Kurahisisha:\(−\frac{45}{81}\).
- Answer
-
\(−\frac{5}{9}\)
Try It \(\PageIndex{15}\)
Kurahisisha:\(−\frac{42}{54}\).
- Jibu
-
\(−\frac{7}{9}\)
Katika sura hii, tutafikiri kwamba maadili yote ya namba ambayo yangefanya denominator kuwa sifuri yameondolewa. Hatuwezi kuandika vikwazo kwa kila kujieleza kwa busara, lakini kukumbuka kwamba denominator haiwezi kamwe kuwa sifuri. Hivyo katika mfano huu ijayo,\(x \ne 0\) na\(y \ne 0\).
Kurahisisha:\(\frac{3xy}{18x^{2}y^{2}}\).
Suluhisho
 |
|
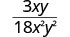| Andika upya nambari na denominator kuonyesha mambo ya kawaida. |  |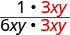
| Kurahisisha kutumia sawa FRACTIONS Mali. |  |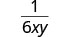
Je, taarifa kwamba hizi ni hatua sawa sisi alichukua wakati sisi kugawanywa monomials katika Polynomials?
Jaribu\(\PageIndex{17}\)
Kurahisisha:\(\frac{4x^{2}y}{12xy^2}\).
- Answer
-
\(\frac{x}{3y}\)
Try It \(PageIndex{18}\)
Kurahisisha:\(\frac{16x^{2}y}{2xy^2}\).
- Jibu
-
\(\frac{8x}{y}\)
Kuwa makini sana kama wewe kuondoa mambo ya kawaida. Mambo yanaongezeka ili kufanya bidhaa. Unaweza kuondoa sababu kutoka kwa bidhaa. Huwezi kuondoa muda kutoka kwa jumla.
Kumbuka kuwa kuondoa x kutoka\(\frac{x+5}{x}\) itakuwa kama kufuta 2 katika sehemu\(\frac{2+5}{2}\)!
Jinsi ya kurahisisha Binomials ya busara
Kurahisisha:\(\frac{2x+8}{5x+20}\).
Suluhisho
Jaribu\(\PageIndex{20}\)
Kurahisisha:\(\frac{3x−6}{2x−4}\).
- Answer
-
\(\frac{3}{2}\)
Try It \(\PageIndex{21}\)
Kurahisisha:\(\frac{7y+35}{5y+25}\).
- Jibu
-
\(\frac{7}{5}\)
Sasa tunafupisha hatua unazopaswa kufuata ili kurahisisha maneno ya busara.
- Fanya namba na denominator kabisa.
- Kurahisisha kwa kugawa mambo ya kawaida.
Tutaweza kutumia mbinu sisi kufunikwa katika Factoring sababu polynomials katika numerators na denominators katika mifano zifuatazo.
Kurahisisha:\(\frac{x^2+5x+6}{x^2+8x+12}\).
Suluhisho
| \(\frac{x^2+5x+6}{x^2+8x+12}\) | |
| Fanya namba na denominator. | \(\frac{(x+2)(x+3)}{(x+2)(x+6)}\) |
| Ondoa sababu ya kawaida x+2 kutoka kwa nambari na denominator. | \(\frac{x+3}{x+6}\) |
Je, unaweza kuwaambia ambayo maadili ya x lazima kutengwa katika mfano huu?
Jaribu\(\PageIndex{23}\)
Kurahisisha:\(\frac{x^2−x−2}{x^2−3x+2}\).
- Answer
-
\(\frac{x+1}{x−1}\)
Try It \(\PageIndex{24}\)
Kurahisisha:\(\frac{x^2−3x−10}{x^2+x−2}\).
- Jibu
-
\(\frac{x−5}{x−1}\)
Kurahisisha:\(\frac{y^2+y−42}{y^2−36}\).
Suluhisho
| \(\frac{y^2+y−42}{y^2−36}\). | |
| Fanya namba na denominator. | \(\frac{(y+7)(y−6)}{(y+6)(y−6)}\) |
| Ondoa jambo la kawaida y-6 kutoka kwa nambari na denominator. | \(\frac{y+7}{y+6}\) |
Jaribu\(\PageIndex{26}\)
Kurahisisha:\(\frac{x^2+x−6}{x^2−4}\).
- Answer
-
\(\frac{x+3}{x+2}\)
Try It \(\PageIndex{27}\)
Kurahisisha:\(\frac{x^2+8x+7}{x^2−49}\).
- Jibu
-
\(\frac{x+1}{x−7}\)
Kurahisisha:\(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\).
Suluhisho
| \(\frac{p^3−2p^2+2p−4}{p^2−7p+10}\) | |
| Fanya namba na denominator, kwa kutumia kikundi ili kuzingatia nambari. | \(\frac{p^2(p−2)+2(p−2)}{(p−5)(p−2)}\) |
| \(\frac{(p^2+2)(p−2)}{(p−5)(p−2)}\) | |
| Ondoa jambo la kawaida p-2 kutoka kwa nambari na denominator. | \(\frac{p^2+2}{p−5}\) |
Jaribu\(\PageIndex{29}\)
Kurahisisha:\(\frac{y^3−3y^2+y−3}{y^2−y−6}\).
- Answer
-
\(\frac{y^2+1}{y+2}\)
Try It \(\PageIndex{30}\)
Kurahisisha:\(\frac{p^3−p^2+2p−2}{p^2+4p−5}\).
- Jibu
-
\(\frac{p^2+2}{p+5}\)
Kurahisisha:\(\frac{2n^2−14n}{4n^2−16n−48}\).
Suluhisho
| \(\frac{2n^2−14n}{4n^2−16n−48}\) | |
| Factor nambari na denominator, kwanza factoring nje GCF. | \(\frac{2n(n−7)}{4(n^2−4n−12)}\) |
| \(\frac{2n(n−7)}{4(n−6)(n+2)}\) | |
| Ondoa jambo la kawaida, 2. | \(\frac{n(n−7)}{2(n−6)(n+2)}\) |
Jaribu\(\PageIndex{32}\)
Kurahisisha:\(\frac{2n^2−10n}{4n^2−16n−20}\).
- Answer
-
\(\frac{n}{2(n+1)}\)
Try It \(\PageIndex{33}\)
Kurahisisha:\(\frac{4x^2−16x}{8x^2−16x−64}\).
- Jibu
-
\(\frac{x}{2(x+2)}\)
Kurahisisha:\(\frac{3b^2−12b+12}{6b^2−24}\).
Suluhisho
| \(\frac{3b^2−12b+12}{6b^2−24}\) | |
| Factor nambari na denominator, kwanza factoring nje GCF. | \(\frac{3(b^2−4b+4)}{6(b^2−4)}\) |
| \(\frac{3(b−2)(b−2)}{6(b−2)(b+2)}\) | |
| Ondoa mambo ya kawaida ya b -2 na 3. | \(\frac{3(b−2)}{2(b+2)}\) |
Jaribu\(\PageIndex{35}\)
Kurahisisha:\(\frac{2x^2−12x+18}{3x^2−27}\).
- Answer
-
\(\frac{2(x−3)}{3(x+3)}\)
Try It \(PageIndex{36}\)
Kurahisisha:\(\frac{5y^2−30y+25}{2y^2−50}\).
- Jibu
-
\(\frac{5(x−1)}{2(x+5)}\)
Kurahisisha:\(\frac{m^3+8}{m^2−4}\).
Suluhisho
| \(\frac{m^3+8}{m^2−4}\) | |
| Fanya namba na denominator, kwa kutumia formula kwa jumla ya cubes na tofauti ya mraba. | \(\frac{(m+2)(m^2−2m+4)}{(m+2)(m−2)}\) |
| Ondoa mambo ya kawaida ya m+2. | \(\frac{m^2−2m+4}{m−2}\) |
Jaribu\(\PageIndex{38}\)
Kurahisisha:\(\frac{p^3−64}{p^2−16}\).
- Answer
-
\(\frac{p^2+4p+16}{p+4}\)
Try It \(\PageIndex{39}\)
Kurahisisha:\(\frac{x^3+8}{x^2−4}\).
- Jibu
-
\(\frac{x^2−2x+4}{x−2}\)
Kurahisisha maneno ya busara na Mambo ya kinyume
Sasa tutaona jinsi ya kurahisisha kujieleza kwa busara ambao nambari na denominator zina mambo tofauti. Hebu tuanze na sehemu ya namba, sema\(\frac{7}{−7}\).
Tunajua sehemu hii simplifies kwa -1. Pia tunatambua kwamba nambari na denominator ni kinyume.
Katika Msingi, tulianzisha nukuu tofauti: kinyume cha ni -a, tunakumbuka pia kwamba —a=,1·a
Sisi kurahisisha sehemu\(\frac{a}{−a}\)
\[\begin{array}{ll} {}&{\frac{a}{−a}}\\ {\text{We could rewrite this.}}&{\frac{1·a}{−1·a}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
Hivyo, kwa njia hiyo hiyo, tunaweza kurahisisha sehemu\(\frac{x−3}{−(x−3)}\)
\[\begin{array}{ll} {}&{\frac{x−3}{−(x−3)}}\\ {\text{We could rewrite this.}}&{\frac{1·(x−3)}{−1·(x−3)}}\\ {\text{Remove the common factors.}}&{\frac{1}{−1}}\\ {\text{Simplify.}}&{−1}\\ \nonumber \end{array}\]
Lakini kinyume cha x-3 kingeweza kuandikwa tofauti:
\[\begin{array}{ll} {}&{−(x−3)}\\ {\text{Distribute.}}&{−x+3}\\ {\text{Rewrite.}}&{3−x}\\ \nonumber \end{array}\]
Hii ina maana sehemu\(\frac{x−3}{3−x}\) simplifies kwa -1.
Kwa ujumla, tunaweza kuandika kinyume cha a-b kama b-a-kwa hiyo usemi wa busara\(\frac{a−b}{b−a}\) unasafisha hadi -1.
Kinyume cha a-b ni b-a
\(\frac{a−b}{b−a}=−1\),\(a \ne b\)
Maneno na mgawanyo wake kinyume na -1
Tutatumia mali hii ili kurahisisha maneno ya busara ambayo yana kinyume katika nambari zao na denominators.
Kurahisisha:\(\frac{x−8}{8−x}\).
Suluhisho
| \(\frac{x−8}{8−x}\). | |
| Tambua kwamba x-8 na 8—x ni kinyume | -1 |
Jaribu\(\PageIndex{41}\)
Kurahisisha:\(\frac{y−2}{2−y}\).
- Answer
-
−1
Try It \(\PageIndex{42}\)
Kurahisisha:\(\frac{n−9}{9−n}\).
- Jibu
-
-1
Kumbuka, hatua ya kwanza katika kurahisisha kujieleza kwa busara ni kuzingatia nambari na denominator kabisa.
Kurahisisha:\(\frac{14−2x}{x^2−49}\).
Suluhisho
 |
|
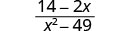| Fanya namba na denominator. |  |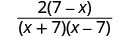
| Kutambua 7—x na x-7 ni kinyume. |  |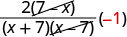
| Kurahisisha. |  |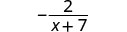
Jaribu\(\PageIndex{44}\)
Kurahisisha:\(\frac{10−2y}{y^2−25}\).
- Answer
-
\(−\frac{2}{y+5}\)
Try It \(\PageIndex{45}\)
Kurahisisha:\(\frac{3y−27}{81−y^2}\).
- Jibu
-
\(−\frac{3}{9+y}\)
Kurahisisha:\(\frac{x^2−4x−32}{64−x^2}\).
Suluhisho
 |
|
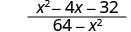| Fanya namba na denominator. |  |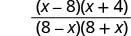
| Tambua mambo ambayo yanapinga. |  |
| Kurahisisha. |  |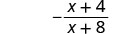
Jaribu\(\PageIndex{47}\)
Kurahisisha:\(\frac{x^2−4x−5}{25−x^2}\).
- Answer
-
\(−\frac{x+1}{x+5}\)
Try It \(\PageIndex{48}\)
Kurahisisha:\(\frac{x^2+x−2}{1−x^2}\).
- Jibu
-
\(−\frac{x+2}{x+1}\)
Dhana muhimu
- Tambua Maadili ambayo Ufafanuzi wa busara haukufafanuliwa
- Weka denominator sawa na sifuri.
- Tatua equation, ikiwa inawezekana.
- Kilichorahisishwa M
- Maneno ya busara yanachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida katika nambari yake na denominator.
- Kurahisisha kujieleza kwa busara
- Fanya namba na denominator kabisa.
- Kurahisisha kwa kugawa mambo ya kawaida.
- Vikwazo katika kujieleza kwa busara
- Kinyume cha a—b ni b-a
\(\frac{a−b}{b−a}=−1\)\(a \ne b\),\(b \ne 0\),\(a \ne b\)
- Kinyume cha a—b ni b-a
Mazoezi hufanya kamili
Katika mazoezi yafuatayo, tambua maadili ambayo maneno ya busara hayajafafanuliwa.
- \(\frac{2x}{z}\)
- \(\frac{4p−1}{6p−5}\)
- \(\frac{n−3}{n^2+2n−8}\)
- Jibu
-
- z=0
- \(p=\frac{5}{6}\)
- n=-4, n=2
- \(\frac{10m}{11n}\)
- \(\frac{6y+13}{4y−9}\)
- \(\frac{b−8}{b^2−36}\)
- \(\frac{4x^{2}y}{3y}\)
- \(\frac{3x−2}{2x+1}\)
- \(\frac{u−1}{u^2−3u−28}\)
- Jibu
-
- y=0
- \(x=−\frac{1}{2}\)
- u=-4, u=7
- \(\frac{5pq^{2}}{9q}\)
- \(\frac{7a−4}{3a+5}\)
- \(\frac{1}{x^2−4}\)
Katika mazoezi yafuatayo, tathmini ya kujieleza kwa busara kwa maadili yaliyotolewa.
\(\frac{2x}{x−1}\)
- x=0
- x=2
- x=-1
- Jibu
-
- 0
- 4
- 1
\(\frac{4y−1}{5y−3}\)
- y=0
- y=2
- y=-1
\(\frac{2p+3}{p^2+1}\)
- p=0
- p=1
- p=-2
- Jibu
-
- 3
- \(\frac{5}{2}\)
- \(−\frac{1}{5}\)
\(\frac{x+3}{2−3x}\)
- x=0
- x=1
- x=-1
\(\frac{y^2+5y+6}{y^2−1}\)
- y=0
- y=2
- y=-2
- Jibu
-
- -6
- \(\frac{20}{3}\)
- 0
\(\frac{z^2+3z−10}{z^2−1}\)
- z=0
- z=2
- z=-2
\(\frac{a^2−4}{a^2+5a+4}\)
- a=0
- a=1
- a=-2
- Jibu
-
- -1
- \(−\frac{3}{10}\)
- 0
\(\frac{b^2+2}{b^2−3b−4}\)
- b=0
- b=2
- b=-2
\(\frac{x^2+3xy+2y^2}{2x^{3}y}\)
- x=1, y=-1
- x=2, y=1
- x=-1, y=-1
- Jibu
-
- 0
- \(\frac{3}{4}\)
- \(\frac{15}{4}\)
\(\frac{c^2+cd−2d^2}{cd^{3}}\)
- c=2, d=-1
- c=1, d=-1
- c=-1, d=2
\(\frac{m^2−4n^2}{5mn^3}\)
- m=2, n=1
- m=-1, n=-1
- m=3, n=2
- Jibu
-
- 0
- \(−\frac{3}{5}\)
- \(−\frac{7}{20}\)
\(\frac{2s^{2}t}{s^2−9t^2}\)
- s=4, t=1
- s=-1, t=-1
- s=0, t=2
Katika mazoezi yafuatayo, kurahisisha.
\(−\frac{4}{52}\)
- Jibu
-
\(−\frac{1}{13}\)
\(−\frac{44}{55}\)
\(\frac{56}{63}\)
- Jibu
-
\(\frac{8}{9}\)
\(\frac{65}{104}\)
\(\frac{6ab^{2}}{12a^{2}b}\)
- Jibu
-
\(\frac{b}{2ab}\)
\(\frac{15xy^{3}}{x^{3}y^{3}}\)
\(\frac{8m^{3}n}{12mn^2}\)
- Jibu
-
\(\frac{2m^2}{3n}\)
\(\frac{36v^{3}w^2}{27vw^3}\)
\(\frac{3a+6}{4a+8}\)
- Jibu
-
\(\frac{3}{4}\)
\(\frac{5b+5}{6b+6}\)
\(\frac{3c−9}{5c−15}\)
- Jibu
-
\(\frac{3}{5}\)
\(\frac{4d+8}{9d+18}\)
\(\frac{7m+63}{5m+45}\)
- Jibu
-
\(\frac{7}{5}\)
\(\frac{8n−96}{3n−36}\)
\(\frac{12p−240}{5p−100}\)
- Jibu
-
\(\frac{12}{5}\)
\(\frac{6q+210}{5q+175}\)
\(\frac{a^2−a−12}{a^2−8a+16}\)
- Jibu
-
\(\frac{a+3}{a−4}\)
\(\frac{x^2+4x−5}{x^2−2x+1}\)
\(\frac{y^2+3y−4}{y^2−6y+5}\)
- Jibu
-
\(\frac{y+4}{y−5}\)
\(\frac{v^2+8v+15}{v^2−v−12}\)
\(\frac{x^2−25}{x^2+2x−15}\)
- Jibu
-
\(\frac{x−5}{x−3}\)
\(\frac{a^2−4}{a^2+6a−16}\)
\(\frac{y^2−2y−3}{y^2−9}\)
- Jibu
-
\(\frac{y+1}{y+3}\)
\(\frac{b^2+9b+18}{b^2−36}\)
\(\frac{y^3+y^2+y+1}{y^2+2y+1}\)
- Jibu
-
\(\frac{y^2+1}{y+1}\)
\(\frac{p^3+3p^2+4p+12}{p^2+p−6}\)
\(\frac{x^3−2x^2−25x+50}{x^2−25}\)
- Jibu
-
x-2
\(\frac{q^3+3q^2−4q−12}{q^2−4}\)
\(\frac{3a^2+15a}{6a^2+6a−36}\)
- Jibu
-
\(\frac{a(a+5)}{2(a+3)(a−2)}\)
\(\frac{8b^2−32b}{2b^2−6b−80}\)
\(\frac{−5c^2−10c}{−10c^2+30c+100}\)
- Jibu
-
\(\frac{c}{2(c−5)}\)
\(\frac{4d^2−24d}{2d^2−4d−48}\)
\(\frac{3m^2+30m+75}{4m^2−100}\)
- Jibu
-
\(\frac{3(m+5)}{4(m−5)}\)
\(\frac{5n^2+30n+45}{2n^2−18}\)
\(\frac{5r^2+30r−35}{r^2−49}\)
- Jibu
-
\(\frac{5(r−1)}{r+7}\)
\(\frac{3s^2+30s+24}{3s^2−48}\)
\(\frac{t^3−27}{t^2−9}\)
- Jibu
-
\(\frac{t^2+3t+9}{t+3}\)
\(\frac{v^3−1}{v^2−1}\)
\(\frac{w^3+216}{w^2−36}\)
- Jibu
-
\(\frac{w^2−6w+36}{w−6}\)
\(\frac{v^3+125}{v^2−25}\)
Kurahisisha maneno ya busara na Mambo ya kinyume
Katika mazoezi yafuatayo, kurahisisha kila kujieleza kwa busara.
\(\frac{a−5}{5−a}\)
- Jibu
-
-1
\(\frac{b−12}{12−b}\)
\(\frac{11−c}{c−11}\)
- Jibu
-
-1
\(\frac{5−d}{d−5}\)
\(\frac{12−2x}{x^2−36}\)
- Jibu
-
\(−\frac{2}{x+6}\)
\(\frac{20−5y}{y^2−16}\)
\(\frac{4v−32}{64−v^2}\)
- Jibu
-
\(−\frac{4}{8+v}\)
\(\frac{7w−21}{9−w^2}\)
\(\frac{y^2−11y+24}{9−y^2}\)
- Jibu
-
\(−\frac{y−8}{3+y}\)
\(\frac{z^2−9z+20}{16−z^2}\)
\(\frac{a^2−5a−36}{81−a^2}\)
- Jibu
-
\(−\frac{a+4}{9+a}\)
\(\frac{b^2+b−42}{36−b^2}\)
kila siku Math
Viwango vya Kodi Kwa mwaka wa kodi 2015, kiasi cha kodi inadaiwa na mtu mmoja anayepata kati ya $37,450 na $90,750, kinaweza kupatikana kwa kutathmini formula 0.25x-4206.25, ambapo x ni mapato. Kiwango cha wastani cha kodi kwa mapato haya kinaweza kupatikana kwa kutathmini formula\(\frac{0.25x−4206.25}{x}\). Je! Kiwango cha wastani cha kodi kwa mtu mmoja anayepata $50,000?
- Jibu
-
16.5%
Kazi urefu wa muda inachukua kwa watu wawili kwa kufanya kazi sawa kama kazi pamoja inaweza kupatikana kwa kutathmini formula\(\frac{xy}{x+y}\). Kama Tom anaweza kuchora tundu katika x=45 dakika na ndugu yake Bobby anaweza kuipaka katika y=dakika 60, itachukua dakika ngapi ikiwa wanafanya kazi pamoja?
Mazoezi ya kuandika
Eleza jinsi unavyopata maadili ya x ambayo kujieleza kwa busara\(\frac{x^2−x−20}{x^2−4}\) haijulikani.
Eleza hatua zote unazochukua ili kurahisisha kujieleza kwa busara\(\frac{p^2+4p−21}{9−p^2}\).
Self Check
ⓐ Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.
ⓑ Kama wengi wa hundi yako walikuwa:
... kwa ujasiri. Hongera! Umefanikiwa malengo yako katika sehemu hii! Fikiria ujuzi wa kujifunza uliyotumia ili uweze kuendelea kuitumia. Ulifanya nini ili uwe na ujasiri wa uwezo wako wa kufanya mambo haya? Kuwa maalum!
... kwa msaada fulani. Hii lazima kushughulikiwa haraka kama mada wewe si bwana kuwa mashimo katika barabara yako ya mafanikio. Math ni mtiririko - kila mada hujenga juu ya kazi ya awali. Ni muhimu kuhakikisha kuwa na msingi imara kabla ya kuendelea. Nani unaweza kuomba msaada? Washiriki wenzako na mwalimu ni rasilimali nzuri. Je, kuna mahali kwenye chuo ambapo waalimu hisabati zinapatikana? Je, ujuzi wako wa kujifunza unaweza kuboreshwa?
... hapana - Siipati! Hii ni muhimu na haipaswi kupuuza. Unahitaji kupata msaada mara moja au utazidiwa haraka. Angalia mwalimu wako haraka iwezekanavyo ili kujadili hali yako. Pamoja unaweza kuja na mpango wa kupata msaada unayohitaji.
faharasa
- kujieleza kwa busara
- Maneno ya busara ni usemi wa fomu\(\frac{p}{q}\), ambapo p na q ni polynomials na\(q \ne 0\).