7.4E: Mazoezi

Last updated
Save as PDF

Page ID: 177526

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Mazoezi hufanya kamili

Factor Perfect Square trinomials

Katika mazoezi yafuatayo, sababu.

Zoezi 1

$16y^2+24y+9$

Jibu: $(4y+3)^2$

Zoezi la 2

$25v^2+20v+4$

Zoezi la 3

$36s^2+84s+49$

Jibu: $(6s+7)^2$

Zoezi la 4

$49s^2+154s+121$

Zoezi 5

$100x^2−20x+1$

Jibu: $(10x−1)^2$

Zoezi la 6

$64z^2−16z+1$

Zoezi la 7

$25n^2−120n+144$

Jibu: $(5n−12)^2$

Zoezi 8

$4p^2−52p+169$

Zoezi la 9

$49x^2−28xy+4y^2$

Jibu: $(7x−2y)^2$

Zoezi 10

$25r^2−60rs+36s^2$

Zoezi 11

$25n^2+25n+4$

Jibu: $(5n+4)(5n+1)$

Zoezi 12

$100y^2−20y+1$

Zoezi 13

$64m^2−16m+1$

Jibu: $(8m-1)^2$

Zoezi 14

$100x^2−25x+1$

Zoezi 15

$10k^2+80k+160$

Jibu: $10(k+4)^2$

Zoezi 16

$64x^2−96x+36$

Zoezi 17

$75u^3−30u^{2}v+3uv^2$

Jibu: $3u(5u−v)^2$

Zoezi 18

$90p^3+300p^{2}q+250pq^2$

Tofauti za Mraba

Katika mazoezi yafuatayo, sababu.

Zoezi la 19

$x^2−16$

Jibu: $(x−4)(x+4)$

Zoezi la 20

$n^2−9$

Zoezi 21

$25v^2−1$

Jibu: $(5v−1)(5v+1)$

Zoezi la 22

$169q^2−1$

Zoezi 23

$121x^2−144y^2$

Jibu: $(11x−12y)(11x+12y)$

Zoezi 24

$49x^2−81y^2$

Zoezi 25

$169c^2−36d^2$

Jibu: $(13c−6d)(13c+6d)$

Zoezi 26

$36p^2−49q^2$

Zoezi 27

$4−49x^2$

Jibu: $(2−7x)(2+7x)$

Zoezi 28

$121−25s^2$

Zoezi 29

$16z^4−1$

Jibu: $(2z−1)(2z+1)(4z^2+1)$

Zoezi 30

$m^4−n^4$

Zoezi 31

$5q^2−45$

Jibu: $5(q−3)(q+3)$

Zoezi 32

$98r^3−72r$

Zoezi la 33

$24p^2+54$

Jibu: $6(4p^2+9)$

Zoezi 34

$20b^2+140$

Kiasi cha Kiasi na Tofauti za Cubes

Katika mazoezi yafuatayo, sababu.

Zoezi 35

$x^3+125$

Jibu: $(x+5)(x^2−5x+25)$

Zoezi 36

$n^3+512$

Zoezi 37

$z^3−27$

Jibu: $(z−3)(z^2+3z+9)$

Zoezi 38

$v^3−216$

Zoezi 39

$8−343t^3$

Jibu: $(2−7t)(4+14t+49t^2)$

Zoezi 40

$125−27w^3$

Zoezi 41

$8y^3−125z^3$

Jibu: $(2y−5z)(4y^2+10yz+25z^2)$

Zoezi 42

$27x^3−64y^3$

Zoezi 43

$7k^3+56$

Jibu: $7(k+2)(k^2−2k+4)$

Zoezi 44

$6x^3−48y^3$

Zoezi 45

$2−16y^3$

Jibu: $2(1−2y)(1+2y+4y^2)$

Zoezi 46

$−2x^3−16y^3$

Mazoezi ya mchanganyiko

Katika mazoezi yafuatayo, sababu.

Zoezi 47

$64a^2−25$

Jibu: $(8a−5)(8a+5)$

Zoezi 48

$121x^2−144$

Zoezi 49

$27q^2−3$

Jibu: $3(3q−1)(3q+1)$

Zoezi 50

$4p^2−100$

Zoezi 51

$16x^2−72x+81$

Jibu: $(4x−9)^2$

Zoezi 52

$36y^2+12y+1$

Zoezi 53

$8p^2+2$

Jibu: $2(4p^2+1)^2$

Zoezi 54

$81x^2+169$

Zoezi 55

$125−8y^3$

Jibu: $(5−2y)(25+10y+4y^2)$

Zoezi 56

$27u^3+1000$

Zoezi 57

$45n^2+60n+20$

Jibu: $5(3n+2)^2$

Zoezi 58

$48q^3−24q^2+3q$

kila siku Math

Zoezi 59

Landscaping Sue na Alan ni mipango ya kuweka$15$ mguu mraba kuogelea katika mashamba yao. Wao watazunguka bwawa na staha ya tiled, upana sawa pande zote. Ikiwa upana wa staha ni$w$, eneo la jumla la bwawa na staha hutolewa na trinomial$4w^2+60w+225$.

Jibu: $(2w+15)^2$

Zoezi 60

Ukarabati wa nyumbani Urefu wa ngazi ya mguu kumi na mbili unaweza kufikia upande wa jengo ikiwa msingi wa ngazi ni$b$ miguu kutoka jengo ni mizizi ya mraba ya binomial$144−b^2$.

Mazoezi ya kuandika

Zoezi 61

Kwa nini ilikuwa muhimu kufanya mazoezi kwa kutumia muundo wa mraba wa binomial katika sura ya kuzidisha polynomials?

Jibu: Majibu yanaweza kutofautiana.

Zoezi 62

Je, unatambua muundo wa mraba wa binomial?

Zoezi 63

Eleza kwa nini$n^2+25 \ne (n+5)^2$.

Jibu: Majibu yanaweza kutofautiana.

Zoezi 64

Maribel ilifanya$y^2−30y+81$ kazi kama (ya-9) ^2. Unajuaje kwamba hii si sahihi?

Self Check

Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

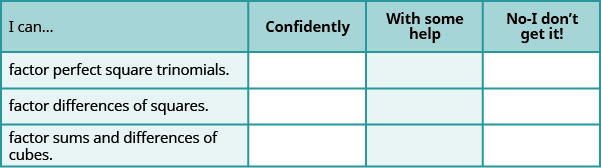
$Jedwali hili lina kauli zifuatazo zote kutanguliwa na “Naweza...”. Mstari wa kwanza ni “trinomials kamili ya mraba”. Mstari wa pili ni “tofauti za mraba”. Mstari wa tatu ni “kiasi cha sababu na tofauti za cubes”. Katika nguzo kando ya kauli hizi ni vichwa, “kwa ujasiri”, “kwa msaada fulani”, na “Hakuna-siipati!”.$

b Kwa kiwango cha 1—10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?