7.4: Factor Maalum Bidhaa
- Page ID
- 177516
Mwishoni mwa sehemu hii, utaweza:
- Factor kamili trinomials mraba
- Sababu tofauti ya mraba
- Kiasi cha sababu na tofauti za cubes
- Chagua njia ya kuzingatia polynomial kabisa
Kabla ya kuanza, fanya jaribio hili la utayari.
- kurahisisha:\((12 x)^{2}\)
Kama amekosa tatizo hili, mapitio Zoezi 6.2.22. - Kuzidisha:\((m+4)^{2}\)
Ikiwa umekosa tatizo hili, kagua Zoezi 6.4.1. - Kuzidisha:\((p-9)^{2}\)
Ikiwa umekosa tatizo hili, kagua Zoezi 6.4.4. - kuzidisha:\((k+3)(k-3)\)
Ikiwa umekosa tatizo hili, kagua Zoezi 6.4.16.
mkakati wa factoring sisi maendeleo katika sehemu ya mwisho itawaongoza wewe kama sababu binomials zaidi, trinomials, na polynomials na maneno zaidi ya tatu. Tumeona kwamba baadhi ya binomials na trinomials matokeo ya bidhaa maalum-squaring binomials na kuzidisha conjugates. Ikiwa unajifunza kutambua aina hizi za polynomials, unaweza kutumia mifumo maalum ya bidhaa ili kuwazingatia kwa haraka zaidi.
Factor Perfect Square trinomials
Baadhi ya trinomials ni mraba kamilifu. Wanatokana na kuzidisha nyakati za binomial yenyewe. Unaweza mraba binomial kwa kutumia FOIL, lakini kwa kutumia muundo wa Mraba wa Binomial uliyoona katika sura ya awali inakuokoa hatua. Hebu tuchunguze muundo wa Mraba ya Binomial kwa kuchanganya binomial kwa kutumia FOIL.
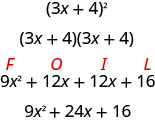
Muda wa kwanza ni mraba wa muda wa kwanza wa binomial na muda wa mwisho ni mraba wa mwisho. Muda wa kati ni mara mbili ya bidhaa za maneno mawili ya binomial.
\[\begin{array}{c}{(3 x)^{2}+2(3 x \cdot 4)+4^{2}} \\ {9 x^{2}+24 x+16}\end{array}\]
The trinomial\(9 x^{2}+24+16\) inaitwa trinomial kamili ya mraba. Ni mraba wa binomial 3 x +4.
Tutaweza kurudia Binomial Mraba Pattern hapa kutumia kama kumbukumbu katika factoring.
Kama na b ni idadi halisi,
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \qquad(a-b)^{2}=a^{2}-2 a b+b^{2}\]
Wakati mraba binomial, bidhaa ni kamili mraba trinomial. Katika sura hii, unajifunza kwa sababu-sasa, utaanza na trinomial kamili ya mraba na kuiingiza katika mambo yake kuu.
Unaweza kuzingatia hii trinomial kwa kutumia mbinu zilizoelezwa katika sehemu ya mwisho, kwani ni ya fomu\(ax^{2}+bx+c\). Lakini ikiwa unatambua kwamba maneno ya kwanza na ya mwisho ni mraba na trinomial inafaa mfano kamili wa mraba wa trinomials, utajiokoa kazi nyingi.
Hapa ni muundo-reverse ya muundo binomial mraba.
Kama na b ni idadi halisi,
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \qquad a^{2}-2 a b+b^{2}=(a-b)^{2}\]
Ili utumie mfano huu, unapaswa kutambua kwamba trinomial iliyotolewa inafaa. Angalia kwanza ili uone kama mgawo wa kuongoza ni mraba kamili,\(a^2\). Next kuangalia kwamba muda wa mwisho ni mraba kamili,\(b^2\). Kisha angalia muda wa kati-ni mara mbili ya bidhaa,\(2ab\)? Ikiwa kila kitu kinachunguza, unaweza kuandika kwa urahisi mambo.
Sababu:\(9 x^{2}+12 x+4\)
- Jibu
-



Sababu:\(4 x^{2}+12 x+9\)
- Jibu
-
\((2 x+3)^{2}\)
Sababu:\(9 y^{2}+24 y+16\)
- Jibu
-
\((3 y+4)^{2}\)
Ishara ya muda wa kati huamua muundo gani tutakayotumia. Wakati muda wa kati ni hasi, tunatumia mfano\(a^{2}-2 a b+b^{2}\), ambayo mambo ya\((a-b)^{2}\).
Hatua hizi zimefupishwa hapa.
\(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
Tutafanya kazi moja sasa ambapo muda wa kati ni hasi.
Sababu:\(81 y^{2}-72 y+16\)
- Jibu
-
Masharti ya kwanza na ya mwisho ni mraba. Angalia kama muda wa kati unafaa mfano wa trinomial kamili ya mraba. Muda wa kati ni hasi, hivyo mraba wa binomial itakuwa\((a-b)^{2}\).
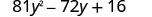
Je, masharti ya kwanza na ya mwisho ni mraba kamili? 
Angalia muda wa kati. 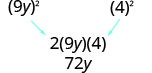
Je, ni mechi\((a-b)^{2}\)? Ndiyo. 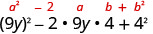
Andika mraba wa binomial. 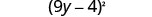
Angalia kwa kuzidisha. \((9 y-4)^{2}\) \((9 y)^{2}-2 \cdot 9 y \cdot 4+4^{2}\) \(81 y^{2}-72 y+16 \checkmark\)
Sababu:\(64 y^{2}-80 y+25\)
- Jibu
-
\((8 y-5)^{2}\)
Sababu:\(16 z^{2}-72 z+81\)
- Jibu
-
\((4 z-9)^{2}\)
Mfano unaofuata utakuwa trinomial kamili ya mraba na vigezo viwili.
Sababu:\(36 x^{2}+84 x y+49 y^{2}\)
- Jibu
-
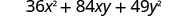
Mtihani kila neno ili kuthibitisha muundo. 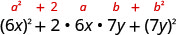
Sababu. 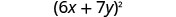
Angalia kwa kuzidisha. \((6 x+7 y)^{2}\) \((6 x)^{2}+2 \cdot 6 x \cdot 7 y+(7 y)^{2}\) \(36 x^{2}+84 x y+49 y^{2} \checkmark\)
Sababu:\(49 x^{2}+84 x y+36 y^{2}\)
- Jibu
-
\((7 x+6 y)^{2}\)
Sababu:\(64 m^{2}+112 m n+49 n^{2}\)
- Jibu
-
\((8 m+7 n)^{2}\)
Sababu:\(9 x^{2}+50 x+25\)
- Jibu
-
\(\begin{array}{lc} & 9 x^{2}+50 x+25 \\ \text { Are the first and last terms perfect squares? } & (3 x)^{2} \qquad\quad (5)^2 \\ \text { Check the middle term-is it 2ab? } & (3 x)^{2} \searrow_{2(3 x)(5) }\swarrow (5)^{2}. \\ & \tiny{30x} \\ \text { No! } 30 x \neq 50 x & \text { This does not fit the pattern! } \\ \text { Factor using the "ac" method. } & 9 x^{2}+50 x+25 \\ \begin{array}{c}{\text { ac }} \\ {\text { Notice: } 9 \cdot 25 \text { and } 5 \cdot 45=225} \\ {225}\end{array} \\ {\text { Split the middle term. }} & \begin{array}{c}{9 x^{2}+5 x+45 x+25} \\ {x(9 x+5)+5(9 x+5)} \\ {(9 x+5)(x+5)}\end{array}\\ {\text { Factor by grouping. }} \\ \text { Check. } & \\ \begin{array}{l}{(9 x+5)(x+5)} \\ {9 x^{2}+45 x+5 x+25} \\ {9 x^{2}+50 x+25}\checkmark\end{array}\end{array}\)
Sababu:\(16 r^{2}+30 r s+9 s^{2}\)
- Jibu
-
\((8 r+3 s)(2 r+3 s)\)
Sababu:\(9 u^{2}+87 u+100\)
- Jibu
-
\((3 u+4)(3 u+25)\)
Kumbuka hatua ya kwanza kabisa katika Mkakati wetu wa Factoring Polynomials? Ilikuwa ni kuuliza “kuna sababu kubwa ya kawaida?” na, kama kulikuwa na, wewe sababu GCF kabla ya kwenda yoyote zaidi. Perfect trinomials mraba inaweza kuwa GCF katika suala zote tatu na ni lazima factored nje kwanza. Na, wakati mwingine, mara GCF imechukuliwa, utatambua trinomial kamili ya mraba.
Sababu:\(36 x^{2} y-48 x y+16 y\)
- Jibu
-
\(36 x^{2} y-48 x y+16 y\) Je, kuna GCF? Ndiyo, 4 y, hivyo factor nje. 4\(y\left(9 x^{2}-12 x+4\right)\) Je, hii ni trinomial mraba kamili? Thibitisha muundo. 
Sababu. 4\(y(3 x-2)^{2}\) Kumbuka: Weka sababu 4 y katika bidhaa ya mwisho. Angalia. \(4y(3 x-2)^{2}\) \(4y[(3 x)^{2}-2 \cdot 3 x \cdot 2+2^{2}]\) \(4 y(9 x)^{2}-12 x+4\) \(36 x^{2} y-48 x y+16 y\checkmark\)
Sababu:\(8 x^{2} y-24 x y+18 y\)
- Jibu
-
2\(y(2 x-3)^{2}\)
Sababu:\(27 p^{2} q+90 p q+75 q\)
- Jibu
-
3\(q(3 p+5)^{2}\)
Tofauti za Mraba
Bidhaa nyingine maalum uliyoyaona katika uliopita ilikuwa mfano wa Bidhaa za Conjugates. Wewe kutumika hii kuzidisha binomials mbili kwamba walikuwa conjugates. Hapa ni mfano:
\[\begin{array}{c}{(3 x-4)(3 x+4)} \\ {9 x^{2}-16}\end{array}\]
Kumbuka, unapozidisha binomials conjugate, maneno ya kati ya bidhaa kuongeza 0. Wote umesalia ni binomial, tofauti ya mraba.
Kuzidisha conjugates ni njia pekee ya kupata binomial kutoka kwa bidhaa ya binomials mbili.
Kama na b ni idadi halisi
\[(a-b)(a+b)=a^{2}-b^{2}\]
Bidhaa inaitwa tofauti ya mraba.
Kwa sababu, tutatumia muundo wa bidhaa “kwa reverse” ili kuzingatia tofauti ya mraba. Tofauti ya mambo ya mraba kwa bidhaa za conjugates.
Kama na b ni idadi halisi,
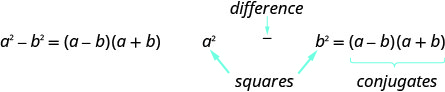
Kumbuka, “tofauti” inahusu kuondoa. Hivyo, kwa kutumia mfano huu lazima kuhakikisha una binomial ambayo mraba mbili ni kuwa suttracted.
Sababu:\(x^{2}-4\)
- Jibu
-




Sababu:\(h^{2}-81\)
- Jibu
-
\((h-9)(h+9)\)
Sababu:\(k^{2}-121\)
- Jibu
-
\((k-11)(k+11)\)
\(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
Ni muhimu kukumbuka kwamba kiasi cha mraba hazizingatii katika bidhaa za binomials. Hakuna mambo ya binomial ambayo huzidisha pamoja ili kupata jumla ya mraba. Baada ya kuondoa GCF yoyote,\(a^{2}+b^{2}\) usemi ni mkuu!
Usisahau kwamba 1 ni mraba kamilifu. Tutahitaji kutumia ukweli huo katika mfano unaofuata.
Sababu:\(64 y^{2}-1\)
- Jibu
-
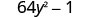
Je, hii ni tofauti? Ndiyo. 
Je, masharti ya kwanza na ya mwisho ni mraba kamili? Ndiyo - waandike kama mraba. 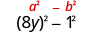
Sababu kama bidhaa ya conjugates. 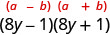
Angalia kwa kuzidisha. \((8 y-1)(8 y+1)\) \(64 y^{2}-1 \checkmark\)
Sababu:\(m^{2}-1\)
- Jibu
-
\((m-1)(m+1)\)
Sababu:\(81 y^{2}-1\)
- Jibu
-
\((9 y-1)(9 y+1)\)
Sababu:\(121 x^{2}-49 y^{2}\)
- Jibu
-
\(\begin{array}{lc} & 121 x^{2}-49 y^{2} \\ \text { Is this a difference of squares? Yes. } & (11 x)^{2}-(7 y)^{2} \\ \text { Factor as the product of conjugates. } & (11 x-7 y)(11 x+7 y) \\ \text { Check by multiplying. } & \\ \begin{array}{l}{(11 x-7 y)(11 x+7 y)} \\ {121 x^{2}-49 y^{2}} \checkmark \end{array} \end{array}\)
Sababu:\(196 m^{2}-25 n^{2}\)
- Jibu
-
\((16 m-5 n)(16 m+5 n)\)
Sababu:\(144 p^{2}-9 q^{2}\)
- Jibu
-
\((12 p-3 q)(12 p+3 q)\)
Binomial katika mfano unaofuata inaweza kuangalia “nyuma,” lakini bado ni tofauti ya mraba.
Sababu:\(100-h^{2}\)
- Jibu
-
\(\begin{array}{lc} & 100-h^{2} \\ \text { Is this a difference of squares? Yes. } & (10)^{2}-(h)^{2}\\ \text { Factor as the product of conjugates. } & (10-h)(10+h)\\ \text { Check by multiplying. } & \\ \begin{array}{l}{(10-h)(10+h)} \\ {100-h^{2}} \checkmark \end{array} \end{array}\)
Kuwa makini kuandika upya kujieleza awali kama\(h^{2}-100\).
Factor\(h^{2}-100\) peke yako na kisha angalia jinsi matokeo hutofautiana na\((10-h)(10+h)\).
Sababu:\(144-x^{2}\)
- Jibu
-
\((12-x)(12+x)\)
Sababu:\(169-p^{2}\)
- Jibu
-
\((13-p)(13+p)\)
Ili kuzingatia kabisa binomial katika mfano unaofuata, tutazingatia tofauti ya mraba mara mbili!
Sababu:\(x^{4}-y^{4}\)
- Jibu
-
\(\begin{array}{lc}\text { Is this a difference of squares? Yes. } & {x^{4}-y^{4}} \\\text { Factor it as the product of conjugates. } & {\left(x^{2}\right)^{2}-\left(y^{2}\right)^{2}} \\ \text { Notice the first binomial is also a difference of squares! } & {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ \text { Factor it as the product of conjugates. The last }& {(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ \text { factor, the sum of squares, cannot be factored. } \\ \\ \text { Check by multiplying. } & \\\begin{array}{l}{(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ {[(x-y)(x+y)]\left(x^{2}+y^{2}\right)} \\ {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ {x^{4}-y^{4}} \checkmark \end{array} \end{array}\)
Sababu:\(a^{4}-b^{4}\)
- Jibu
-
\(\left(a^{2}+b^{2}\right)(a+b)(a-b)\)
Sababu:\(x^{4}-16\)
- Jibu
-
\(\left(x^{2}+4\right)(x+2)(x-2)\)
Kama siku zote, unapaswa kuangalia sababu ya kawaida kwanza wakati wowote una kujieleza kwa sababu. Wakati mwingine sababu ya kawaida inaweza “kujificha” tofauti ya mraba na huwezi kutambua mraba kamilifu mpaka utakapofanya GCF.
Sababu:\(8 x^{2} y-98 y\)
- Jibu
-
\(\begin{array}{lc}& 8 x^{2} y-98 y \\ \text { Is there a GCF? Yes, } 2 y-\text { factor it out! } & 2 y\left(4 x^{2}-49\right) \\ \text { Is the binomial a difference of squares? Yes. } & 2 y\left((2 x)^{2}-(7)^{2}\right) \\ \text { Factor as a product of conjugates. } & 2 y(2 x-7)(2 x+7) \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{2 y(2 x-7)(2 x+7)} \\ {2 y[(2 x-7)(2 x+7)]} \\ {2 y\left(4 x^{2}-49\right)} \\ {8 x^{2} y-98 y} \checkmark \end{array} \end{array}\)
Sababu:\(7 x y^{2}-175 x\)
- Jibu
-
7\(x(y-5)(y+5)\)
Sababu:\(45 a^{2} b-80 b\)
- Jibu
-
5\(b(3 a-4)(3 a+4)\)
Sababu:\(6 x^{2}+96\)
- Jibu
-
\(\begin{array}{lc}&6 x^{2}+96 \\ \text { Is there a GCF? Yes, } 6-\text { factor it out! } & 6\left(x^{2}+16\right) \\ \text { Is the binomial a difference of squares? No, it } & \\ \text { is a sum of squares. Sums of squares do not factor! } & \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{6\left(x^{2}+16\right)} \\ {6 x^{2}+96 }\checkmark \end{array} \end{array}\)
Sababu:\(8 a^{2}+200\)
- Jibu
-
8\(\left(a^{2}+25\right)\)
Sababu:\(36 y^{2}+81\)
- Jibu
-
9\(\left(4 y^{2}+9\right)\)
Kiasi cha Kiasi na Tofauti za Cubes
Kuna mfano mwingine maalum kwa ajili ya factoring, moja ambayo hatukutumia wakati sisi kuzidisha polynomials. Hii ni mfano wa jumla na tofauti ya cubes. Tutaandika kanuni hizi kwanza na kisha tuangalie kwa kuzidisha.
\[\begin{aligned} a^{3}+b^{3} &=(a+b)\left(a^{2}-a b+b^{2}\right) \\ a^{3}-b^{3} &=(a-b)\left(a^{2}+a b+b^{2}\right) \end{aligned}\]
Tutaangalia muundo wa kwanza na kuacha pili kwako.
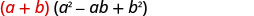 |
|
| Kusambaza. |  |
| Kuzidisha. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| Kuchanganya kama maneno. | \(a^{3}+b^{3}\) |
\[\begin{array}{l}{a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)} \\ {a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)}\end{array}\]
Mwelekeo wawili huonekana sawa, sivyo? Lakini angalia ishara katika mambo. Ishara ya sababu ya binomial inafanana na ishara katika binomial ya awali. Na ishara ya muda wa kati ya sababu ya trinomial ni kinyume cha ishara katika binomial ya awali. Ikiwa unatambua mfano wa ishara, inaweza kukusaidia kukariri ruwaza.

Sababu ya trinomial katika jumla na tofauti ya muundo wa cubes haiwezi kuhesabiwa.
Inaweza kuwa na manufaa sana ikiwa unajifunza kutambua cubes ya integers kutoka 1 hadi 10, kama vile umejifunza kutambua mraba. Tumeorodhesha cubes ya integers kutoka 1 hadi 10 katika Kielelezo\(\PageIndex{1}\).

Sababu:\(x^{3}+64\)
- Jibu
-





Sababu:\(x^{3}+27\)
- Jibu
-
\((x+3)\left(x^{2}-3 x+9\right)\)
Sababu:\(y^{3}+8\)
- Jibu
-
\((y+2)\left(y^{2}-2 y+4\right)\)
Ili kuzingatia jumla au tofauti ya cubes:
- Je, binomial inafaa jumla au tofauti ya muundo wa cubes?
- Je, ni jumla au tofauti?
- Je, maneno ya kwanza na ya mwisho ni cubes kamili?
- Waandike kama cubes.
- Tumia ama jumla au tofauti ya muundo wa cubes.
- Kurahisisha ndani ya mabano
- Angalia kwa kuzidisha mambo.
Sababu:\(: x^{3}-1000\)
- Jibu
-

Hii binomial ni tofauti. Masharti ya kwanza na ya mwisho ni cubes kamilifu. Andika maneno kama cubes. 
Tumia tofauti ya muundo wa cubes. 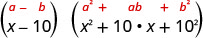
Kurahisisha. 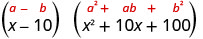
Angalia kwa kuzidisha. 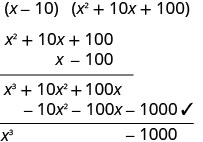
Sababu:\(u^{3}-125\)
- Jibu
-
\((u-5)\left(u^{2}+5 u+25\right)\)
Sababu:\(v^{3}-343\)
- Jibu
-
\((v-7)\left(v^{2}+7 v+49\right)\)
Kuwa makini kutumia ishara sahihi katika sababu za jumla na tofauti ya cubes.
Sababu:\(512-125 p^{3}\)
- Jibu
-

Hii binomial ni tofauti. Masharti ya kwanza na ya mwisho ni cubes kamilifu. Andika maneno kama cubes. 
Tumia tofauti ya muundo wa cubes. 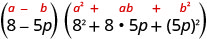
Kurahisisha. 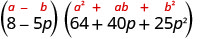
Angalia kwa kuzidisha. Tutaacha hundi kwako.
Sababu:\(64-27 x^{3}\)
- Jibu
-
\((4-3 x)\left(16+12 x+9 x^{2}\right)\)
Sababu:\(27-8 y^{3}\)
- Jibu
-
\((3-2 y)\left(9+6 y+4 y^{2}\right)\)
Sababu:\(27 u^{3}-125 v^{3}\)
- Jibu
-

Hii binomial ni tofauti. Masharti ya kwanza na ya mwisho ni cubes kamilifu. Andika maneno kama cubes. 
Tumia tofauti ya muundo wa cubes. 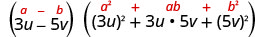
Kurahisisha. 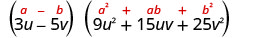
Angalia kwa kuzidisha. Tutaacha hundi kwako.
Sababu:\(8 x^{3}-27 y^{3}\)
- Jibu
-
\((2 x-3 y)\left(4 x^{2}+6 x y+9 y^{2}\right)\)
Sababu:\(1000 m^{3}-125 n^{3}\)
- Jibu
-
\((10 m-5 n)\left(100 m^{2}+50 m n+25 n^{2}\right)\)
Katika mfano unaofuata, sisi kwanza sababu nje GCF. Kisha tunaweza kutambua jumla ya cubes.
Sababu:\(5 m^{3}+40 n^{3}\)
- Jibu
-
Angalia. Kuangalia, unaweza kupata rahisi kuzidisha jumla ya mambo ya cubes kwanza, kisha uongeze bidhaa hiyo kwa 5. Tutaacha kuzidisha kwako.
Factor sababu ya kawaida. 
Binomial hii ni jumla. Masharti ya kwanza na ya mwisho ni cubes kamilifu. Andika maneno kama cubes. 
Tumia jumla ya muundo wa cubes. 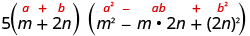
Kurahisisha. 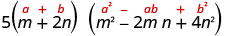
- 5\((m+2 n)\left(m^{2}-2 m n+4 n^{2}\right)\)
Sababu:\(500 p^{3}+4 q^{3}\)
- Jibu
-
4\((5 p+q)\left(25 p^{2}-5 p q+q^{2}\right)\)
Sababu:\(432 c^{3}+686 d^{3}\)
- Jibu
-
2\((6 c+7 d)\left(36 c^{2}-42 c d+49 d^{2}\right)\)
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na factoring bidhaa maalum.
- Jumla ya Tofauti ya Cubes
- Tofauti ya Cubes Factoring
Dhana muhimu
- Factor kamili trinomials mraba Angalia Mfano. \(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
- Factor tofauti ya mraba Angalia Mfano. \(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
- Factor jumla na tofauti ya cubes Kwa sababu jumla au tofauti ya cubes: Angalia Mfano.
- Je, binomial inafaa jumla au tofauti ya muundo wa cubes? Je, ni jumla au tofauti? Je, maneno ya kwanza na ya mwisho ni cubes kamili?
- Waandike kama cubes.
- Tumia ama jumla au tofauti ya muundo wa cubes.
- Kurahisisha ndani ya mabano
- Angalia kwa kuzidisha mambo.
faharasa
- kamili ya mraba trinomials mfano
- Kama na b ni idadi halisi,
\[\begin{array}{cc} {a^2+2ab+b^2=(a+b)^2}&{a^2−2ab+b^2=(a−b)^2}\\ \nonumber \end{array}\]
- tofauti ya muundo wa mraba
- Kama na b ni idadi halisi,

- jumla na tofauti ya muundo wa cubes
-
\[\begin{array}{cc} {a^3+b^3=(a+b)(a^2−ab+b^2)}&{a^3−b^3=(a−b)(a^2+ab+b^2)}\\ \nonumber \end{array}\]


