7.5: Mkakati Mkuu wa kuzingatia Polynomials

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Kutambua na kutumia njia sahihi kwa sababu ya polynomial kabisa

Kumbuka

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Factor$y^{2}-2 y-24$.
   Kama amekosa tatizo hili, kupitia Zoezi 7.2.19.
2. Factor$3 t^{2}+17 t+10$.
   Kama amekosa tatizo hili, kupitia Zoezi 7.3.28.
3. Factor$36 p^{2}-60 p+25$.
   Ikiwa umekosa tatizo hili, tathmini Zoezi 7.4.1.
4. Factor$5 x^{2}-80$.
   Kama amekosa tatizo hili, kupitia Zoezi 7.4.31.

Kutambua na Tumia Njia sahihi ya Kufanya Kipolynomial Kikamilifu

Sasa umejifunza njia zote za kuzingatia ambazo utahitaji katika kozi hii. (Katika kozi yako ijayo ya algebra, mbinu zaidi zitaongezwa kwenye repertoire yako.) Takwimu hapa chini inafupisha njia zote za factoring ambazo tumefunikwa. Kielelezo$\PageIndex{1}$ muhtasari mkakati unapaswa kutumia wakati factoring polynomials.

Kielelezo$\PageIndex{1}$

SABABU POLYNOMIALS.

1. Je, kuna sababu kubwa ya kawaida?
   • Factor ni nje.
2. Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
   • Kama ni binomial: Je,
     ni jumla?
     • Ya mraba? Sums ya mraba si sababu.
     • Ya cubes? Tumia jumla ya muundo wa cubes.
     Je, ni tofauti?
     • Ya mraba? Sababu kama bidhaa ya conjugates.
     • Ya cubes? Tumia tofauti ya muundo wa cubes.
   • Ikiwa ni trinomial: Je,
     ni ya fomu$x^{2}+b x+c ?$? Tengeneza FOIL.
     Je, ni ya fomu$a x^{2}+b x+c$?
     • Ikiwa aa na c ni mraba, angalia ikiwa inafaa muundo wa mraba wa trinomial.
     • Tumia jaribio na hitilafu au njia ya “ac”.
   • Ikiwa ina maneno zaidi ya tatu:
     Tumia njia ya kikundi.
3. Angalia.
   • Je, ni sababu kabisa?
   • Je! Sababu zinazidisha nyuma ya polynomial ya awali?

Kumbuka, polynomial inaelezewa kabisa ikiwa, isipokuwa monomials, mambo yake ni mkuu!

Zoezi$\PageIndex{1}$

Sababu kabisa:$4 x^{5}+12 x^{4}$

Jibu

\ (\ kuanza {safu} {lll}\ maandishi {Je, kuna GCF? } &\ Nakala {Ndiyo,} 4 x ^ {4} & 4 x ^ {5} +12 x ^ {4}\\ Nakala {Factor nje GCF.} & &4 x^ {4} (x+3)\\ maandishi {Katika mabano, ni binomial, a} & &\\ Nakala {trinomial, au kuna maneno zaidi ya tatu? } &\ maandishi {Binomial.} &\\ quad\\ Nakala {Je, ni jumla? } & &\ Nakala {Ndiyo.}\\ quad\ Nakala {Ya mraba? Ya cubes? } & &\ Nakala {Hapana.}\\ Nakala {Angalia.}
\\\\ quad\\ Nakala {Je, maneno yanafanywa kabisa? } & &\ maandishi {Ndiyo.}\\ quad\\ Nakala {Kuzidisha.}\\ kuanza {safu} {l} {4 x ^ {4} (x+3)}\\ {4 x^ {4}\ cdot x+4 x ^ {4}\ cdot 3}\\ {4 x^ {5} +12 x^ {4}}\ alama ya mwisho {4}\ mwisho {safu}\)

Zoezi$\PageIndex{2}$

Sababu kabisa:$3 a^{4}+18 a^{3}$

Jibu

3$a^{3}(a+6)$

Zoezi$\PageIndex{3}$

Sababu kabisa:$45 b^{6}+27 b^{5}$

Jibu

9$b^{5}(5 b+3)$

Zoezi$\PageIndex{4}$

Sababu kabisa:$12 x^{2}-11 x+2$

Jibu

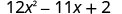
Je, kuna GCF?	Hapana.
Je, ni binomial, trinomial, au kuna maneno zaidi ya tatu?	Trinomial.
Je na c mraba kamili?	Hapana, a = 12, si mraba kamili.
Tumia jaribio na hitilafu au njia ya “ac”. Tutatumia jaribio na hitilafu hapa.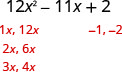

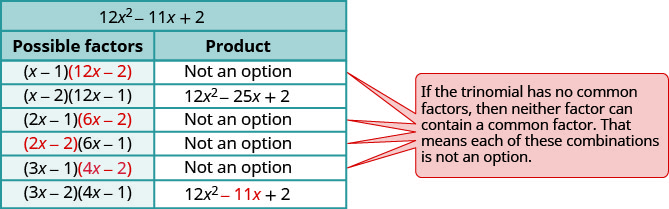
Angalia. $\begin{array}{l}{(3 x-2)(4 x-1)} \\ {12 x^{2}-3 x-8 x+2} \\ {12 x^{2}-11 x+2 }\checkmark \end{array}$

Zoezi$\PageIndex{5}$

Sababu kabisa:$10 a^{2}-17 a+6$

Jibu

$(5 a-6)(2 a-1)$

Zoezi$\PageIndex{6}$

Sababu kabisa:$8 x^{2}-18 x+9$

Jibu

$(2 x-3)(4 x-3)$

Zoezi$\PageIndex{7}$

Sababu kabisa:$g^{3}+25 g$

Jibu

$\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, g.} &g^{3}+25 g \\\text { Factor out the GCF. } & &g\left(g^{2}+25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \quad \text { Is it a sum? Of squares? } & \text { Yes. } & \text { Sums of squares are prime. } \\\text { Check. } \\ \\ \quad \text { Is the expression factored completely? } &\text { Yes. } \\ \quad \text { Multiply. } \\ \qquad \begin{array}{l}{g\left(g^{2}+25\right)} \\ {g^{3}+25 g }\checkmark \end{array} \end{array}$

Zoezi$\PageIndex{8}$

Sababu kabisa:$x^{3}+36 x$

Jibu

$x\left(x^{2}+36\right)$

Zoezi$\PageIndex{9}$

Sababu kabisa:$27 y^{2}+48$

Jibu

3$\left(9 y^{2}+16\right)$

Zoezi$\PageIndex{10}$

Sababu kabisa:$12 y^{2}-75$

Jibu

$\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 3.} &12 y^{2}-75 \\\text { Factor out the GCF. } & &3\left(4 y^{2}-25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \text { Is it a sum?} & \text { No. } & \\ \text { Is it a difference? Of squares or cubes? } &\text { Yes, squares. } & 3\left((2 y)^{2}-(5)^{2}\right) \\ \text { Write as a product of conjugates. } & &3(2 y-5)(2 y+5)\\\text { Check. } \\ \\ \text { Is the expression factored completely? } & \text{ Yes.}& \\ \text { Neither binomial is a difference of } \\ \text { squares. } \\ \text{ Multiply.} \\ \quad \begin{array}{l}{3(2 y-5)(2 y+5)} \\ {3\left(4 y^{2}-25\right)} \\ {12 y^{2}-75}\checkmark \end{array} \end{array}$

Zoezi$\PageIndex{11}$

Sababu kabisa:$16 x^{3}-36 x$

Jibu

4$x(2 x-3)(2 x+3)$

Zoezi$\PageIndex{12}$

Sababu kabisa:$27 y^{2}-48$

Jibu

3$(3 y-4)(3 y+4)$

Zoezi$\PageIndex{13}$

Sababu kabisa:$4 a^{2}-12 a b+9 b^{2}$

Jibu

Je, kuna GCF?	Hapana.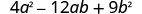
Je, ni binomial, trinomial, au kuna maneno zaidi?
Trinomial na$a\neq 1$. Lakini muda wa kwanza ni mraba kamilifu.
Je, muda wa mwisho ni mraba kamili?	Ndiyo.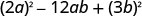
Je, inafaa mfano,$a^{2}-2 a b+b^{2}$?	Ndiyo.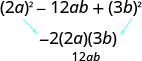
Andika kama mraba.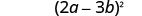
Angalia jibu lako.
Je! Maneno yanafanyika kabisa?
Ndiyo.
Binomial si tofauti ya mraba.
Kuzidisha.
$(2 a-3 b)^{2}$
$(2 a)^{2}-2 \cdot 2 a \cdot 3 b+(3 b)^{2}$
$4 a^{2}-12 a b+9 b^{2} \checkmark$

Zoezi$\PageIndex{14}$

Sababu kabisa:$4 x^{2}+20 x y+25 y^{2}$

Jibu

$(2 x+5 y)^{2}$

Zoezi$\PageIndex{15}$

Sababu kabisa:$9 m^{2}+42 m n+49 n^{2}$

Jibu

$(3 m+7 n)^{2}$

Zoezi$\PageIndex{16}$

Sababu kabisa:$6 y^{2}-18 y-60$

Jibu

$\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 6.} &6 y^{2}-18 y-60 \\\text { Factor out the GCF. } & \text { Trinomial with leading coefficient } 1&6\left(y^{2}-3 y-10\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more terms? } & & \\ \text { "Undo' FOIL. } & 6(y\qquad )(y\qquad ) &6(y+2)(y-5) \\ \text { Check your answer. } \\ \text { Is the expression factored completely? } & & \text{ Yes.} \\ \text { Neither binomial is a difference of squares. } \\ \text { Multiply. } \\ \\\qquad \begin{array}{l}{6(y+2)(y-5)} \\ {6\left(y^{2}-5 y+2 y-10\right)} \\ {6\left(y^{2}-3 y-10\right)} \\ {6 y^{2}-18 y-60} \checkmark \end{array} \end{array}$

Zoezi$\PageIndex{17}$

Sababu kabisa:$8 y^{2}+16 y-24$

Jibu

8$(y-1)(y+3)$

Zoezi$\PageIndex{18}$

Sababu kabisa:$5 u^{2}-15 u-270$

Jibu

5$(u-9)(u+6)$

Zoezi$\PageIndex{19}$

Sababu kabisa:$24 x^{3}+81$

Jibu

Je, kuna GCF?	Ndiyo, 3.	$24 x^{3}+81$
Factor ni nje.		3$\left(8 x^{3}+27\right)$
Katika mabano, ni binomial, trinomial, au kuna maneno zaidi ya tatu?	Binomial.
Je, ni jumla au tofauti?	Jumla.
Ya mraba au cubes?	Jumla ya cubes.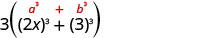
Andika kwa kutumia jumla ya muundo wa cubes.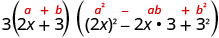
Je! Maneno yanafanywa kabisa?	Ndiyo.	3$(2 x+3)\left(4 x^{2}-6 x+9\right)$
Angalia kwa kuzidisha.		Tunaacha hundi kwako.

Zoezi$\PageIndex{20}$

Sababu kabisa:$250 m^{3}+432$

Jibu

2$(5 m+6)\left(25 m^{2}-30 m+36\right)$

Zoezi$\PageIndex{21}$

Sababu kabisa:$81 q^{3}+192$

Jibu

$3(3q+4)\left(9q^{2}-12 q+16\right)$

Zoezi$\PageIndex{22}$

Sababu kabisa:$2 x^{4}-32$

Jibu

$\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &2 x^{4}-32 \\\text { Factor out the GCF. } & &2\left(x^{4}-16\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } & \text { Binomial. }& \\ \text { Is it a sum or difference? } &\text { Yes. }& \\\text { Of squares or cubes? } & \text { Difference of squares. } & 2\left(\left(x^{2}\right)^{2}-(4)^{2}\right) \\ \text { Write it as a product of conjugates. } & & 2\left(x^{2}-4\right)\left(x^{2}+4\right) \\ \text { The first binomial is again a difference of squares. } & & 2\left((x)^{2}-(2)^{2}\right)\left(x^{2}+4\right) \\ \text { Write it as a product of conjugates. } & & 2(x-2)(x+2)\left(x^{2}+4\right) \\ \text { Is the expression factored completely? } &\text { Yes. } & \\ \\ \text { None of these binomials is a difference of squares. } \\ \text { Check your answer. } \\ \text{ Multiply. }\\ \\ \qquad \qquad \begin{array}{l}{2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-10)} \\ {2 x^{4}-32} \checkmark \end{array} \end{array}$

Zoezi$\PageIndex{23}$

Sababu kabisa:$4 a^{4}-64$

Jibu

4$\left(a^{2}+4\right)(a-2)(a+2)$

Zoezi$\PageIndex{24}$

Sababu kabisa:$7 y^{4}-7$

Jibu

7$\left(y^{2}+1\right)(y-1)(y+1)$

Zoezi$\PageIndex{25}$

Sababu kabisa:$3 x^{2}+6 b x-3 a x-6 a b$

Jibu

$\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 3.} &3 x^{2}+6 b x-3 a x-6 a b\\\text { Factor out the GCF. } & &3\left(x^{2}+2 b x-a x-2 a b\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { More than } 3 & \\ \text { or are there more terms? } &\text { terms. } & \\ \text { Use grouping. } & & \begin{array}{c}{3[x(x+2 b)-a(x+2 b)]} \\ {3(x+2 b)(x-a)}\end{array} \\ \text { Check your answer. } \\ \\ \text { Is the expression factored completely? Yes. } \\ \text { Multiply. } \\\qquad \qquad \begin{array}{l}{3(x+2 b)(x-a)} \\ {3\left(x^{2}-a x+2 b x-2 a b\right)} \\ {3 x^{2}-3 a x+6 b x-6 a b} \checkmark \end{array}\end{array}$

Zoezi$\PageIndex{26}$

Sababu kabisa:$6 x^{2}-12 x c+6 b x-12 b c$

Jibu

6$(x+b)(x-2 c)$

Zoezi$\PageIndex{27}$

Sababu kabisa:$16 x^{2}+24 x y-4 x-6 y$

Jibu

2$(4 x-1)(x+3 y)$

Zoezi$\PageIndex{28}$

Sababu kabisa:$10 x^{2}-34 x-24$

Jibu

$\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &10 x^{2}-34 x-24\\\text { Factor out the GCF. } & &2\left(5 x^{2}-17 x-12\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { Trinomial with } & \\ \text { or are there more than three terms? } &\space a \neq 1 & \\ \text { Use trial and error or the "ac" method. } & & 2\left(5 x^{2}-17 x-12\right) \\ & & 2(5 x+3)(x-4) \\ \text { Check your answer. Is the expression factored } \\\text { completely? Yes. }\\ \\ \text { Multiply. } \\ \qquad \begin{array}{l}{2(5 x+3)(x-4)} \\ {2\left(5 x^{2}-20 x+3 x-12\right)} \\ {2\left(5 x^{2}-17 x-12\right)} \\ {10 x^{2}-34 x-24}\checkmark \end{array}\end{array}$

Zoezi$\PageIndex{29}$

Sababu kabisa:$4 p^{2}-16 p+12$

Jibu

4$(p-1)(p-3)$

Zoezi$\PageIndex{30}$

Sababu kabisa:$6 q^{2}-9 q-6$

Jibu

3$(q-2)(2 q+1)$

Dhana muhimu

• General Mkakati wa factoring Polynomials Angalia Kielelezo$\PageIndex{1}$.
• Jinsi ya Kufanya Polynomials
  1. Je, kuna sababu kubwa ya kawaida? Factor ni nje.
  2. Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
     • Kama ni binomial: Je,
       ni jumla?
       • Ya mraba? Jumla ya mraba si sababu.
       • Ya cubes? Tumia jumla ya muundo wa cubes.
       Je, ni tofauti?
       • Ya mraba? Sababu kama bidhaa ya conjugates.
       • Ya cubes? Tumia tofauti ya muundo wa cubes.
     • Ikiwa ni trinomial: Je,
       ni ya fomu$x^{2}+b x+c$? Tengeneza FOIL.
       Je, ni ya fomu$a x^{2}+b x+c$?
       • Ikiwa 'a' na 'c' ni mraba, angalia ikiwa inafaa muundo wa mraba wa trinomial.
       • Tumia jaribio na hitilafu au njia ya 'ac'.
     • Ikiwa ina maneno zaidi ya tatu:
       Tumia njia ya kikundi.
  3. Angalia. Je, ni sababu kabisa? Je! Sababu zinazidisha nyuma ya polynomial ya awali?