5.4: Tatua Maombi na Mifumo ya Equations

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Tafsiri kwa mfumo wa equations
• Kutatua maombi ya moja kwa moja tafsiri
• Tatua maombi ya jiometri
• Kutatua maombi ya mwendo sare

Kumbuka

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Jumla ya mara mbili namba na tisa ni 31. Pata nambari.
   Ikiwa umekosa tatizo hili, tathmini Zoezi 3.1.10.
2. Twins Jon na Ron pamoja chuma $96,000 mwaka jana. Ron chuma $8,000 zaidi ya mara tatu kile Jon chuma. Je! Kila mapacha alipata kiasi gani?
   Kama amekosa tatizo hili, mapitio Zoezi 3.1.31.
3. Alessio anasimama\(3\frac{1}{2}\) masaa yake ya baiskeli kwa kiwango cha maili 10 kwa saa. Je, alipanda mbali gani?
   Ikiwa umekosa tatizo hili, tathmini Zoezi 2.6.1.

Hapo awali katika sura hii tulitatua maombi kadhaa na mifumo ya equations linear. Katika sehemu hii, tutaweza kuangalia baadhi ya aina maalum ya maombi ambayo yanahusiana kiasi mbili. Tutafsiri maneno katika equations linear, kuamua ni njia gani rahisi zaidi ya kutumia, na kisha kutatua yao.

Tutatumia Mkakati wetu wa Kutatua Tatizo kwa Mifumo ya Ulinganisho wa Mstari.

TUMIA MKAKATI WA KUTATUA TATIZO KWA MIFUMO YA EQUATIONS LINEAR.

1. Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
2. Tambua kile tunachotafuta.
3. Jina kile tunachotafuta. Chagua vigezo ili kuwakilisha kiasi hicho.
4. Tafsiri katika mfumo wa equations.
5. Tatua mfumo wa equations kwa kutumia mbinu nzuri za algebra.
6. Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
7. Jibu swali kwa sentensi kamili.

Tafsiri kwa Mfumo wa Ulinganisho

Matatizo mengi tuliyotatuliwa katika maombi ya awali yanahusiana na kiasi mbili. Hapa ni mifano miwili kutoka sura ya Math Models.

• Jumla ya namba mbili ni hasi kumi na nne. Nambari moja ni nne chini ya nyingine. Kupata idadi.
• Wanandoa wa ndoa pamoja hupata $110,000 kwa mwaka. Mke hupata $16,000 chini ya mara mbili yale mumewe anayopata. Mume anapata nini?

Katika sura hiyo sisi kutafsiriwa kila hali katika equation moja kwa kutumia variable moja tu. Wakati mwingine ilikuwa kidogo ya changamoto kuhesabia jinsi ya jina kiasi mbili, haikuwa hivyo?

Hebu tuone jinsi tunaweza kutafsiri matatizo haya mawili katika mfumo wa milinganyo na vigezo viwili. Tutazingatia Hatua za 1 kupitia 4 za Mkakati wetu wa Kutatua matatizo.

Zoezi\(\PageIndex{1}\): How to Translate to a System of Equations

Tafsiri kwa mfumo wa equations:

Jumla ya namba mbili ni hasi kumi na nne. Nambari moja ni nne chini ya nyingine. Kupata idadi.

Jibu

Zoezi\(\PageIndex{2}\)

Tafsiri kwa mfumo wa equations:

Jumla ya namba mbili ni hasi ishirini na tatu. Nambari moja ni 7 chini ya nyingine. Kupata idadi.

Jibu

\(\left\{\begin{array}{l}{m+n=-23} \\ {m=n-7}\end{array}\right.\)

Zoezi\(\PageIndex{3}\)

Tafsiri kwa mfumo wa equations:

Jumla ya namba mbili ni hasi kumi na nane. Nambari moja ni 40 zaidi ya nyingine. Kupata idadi.

Jibu

\(\left\{\begin{array}{l}{m+n=-18} \\ {m=n+40}\end{array}\right.\)

Tutafanya mfano mwingine ambapo sisi kuacha baada ya sisi kuandika mfumo wa equations.

Zoezi\(\PageIndex{4}\)

Tafsiri kwa mfumo wa equations:

Wanandoa wa ndoa pamoja hupata $110,000 kwa mwaka. Mke hupata $16,000 chini ya mara mbili yale mumewe anayopata. Mume anapata nini?

Jibu

\(\begin{array}{ll}{\text {We are looking for the amount that }} & {\text {Let } h=\text { the amount the husband earns. }} \\ {\text {the husband and wife each earn. }} & { w=\text { the amount the wife earns }} \\ {\text{Translate.}} & {\text{A married couple together earns \$110,000.} }\\ {} & {w+h=110000} \\ & \text{The wife earns \$16,000 less than twice what} \\ & \text{husband earns.} \\ & w=2h−16,000 \\ \text{The system of equations is:} & \left\{\begin{array}{l}{w+h=110,000} \\ {w=2 h-16,000}\end{array}\right.\end{array}\)

Zoezi\(\PageIndex{5}\)

Tafsiri kwa mfumo wa equations:

Wanandoa wana jumla ya mapato ya kaya ya $84,000. Mume hupata $18,000 chini ya mara mbili kile mke anachopata. Je, mke hupata kiasi gani?

Jibu

\(\left\{\begin{array}{l}{w+h=84,000} \\ {h=2 w-18,000}\end{array}\right.\)

Zoezi\(\PageIndex{6}\)

Tafsiri kwa mfumo wa equations:

mfanyakazi mwandamizi hufanya $5 chini ya mara mbili kile mfanyakazi mpya hufanya kwa saa. Pamoja hufanya $43 kwa saa. Ni kiasi gani kila mfanyakazi hufanya kwa saa?

Jibu

\(\left\{\begin{array}{l}{s=2 n-5} \\ {s+n=43}\end{array}\right.\)

Kutatua maombi ya moja kwa moja tafsiri

Sisi kuanzisha, lakini hakuwa na kutatua, mifumo ya equations katika Zoezi\(\PageIndex{1}\) na Zoezi\(\PageIndex{4}\) Sasa tutaweza kutafsiri hali kwa mfumo wa equations na kisha kutatua.

Zoezi\(\PageIndex{7}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Devon ana umri wa miaka 26 kuliko mwanawe Cooper. Jumla ya umri wao ni 50. Kupata umri wao.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	Sisi ni kuangalia kwa miaka ya Devon na Cooper.
Hatua ya 3. Jina kile tunachotafuta.	Hebu d= umri Devon ya. c= umri wa Cooper
Hatua ya 4. Tafsiri katika mfumo wa equations.	Devon ana umri wa miaka 26 kuliko Cooper.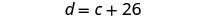
	Jumla ya umri wao ni 50.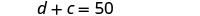
Mfumo ni: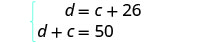
Hatua ya 5. Tatua mfumo wa equations. Tatua kwa kubadilisha.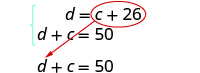
Mbadala c + 26 katika equation ya pili.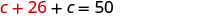
Tatua kwa c.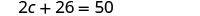
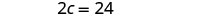
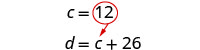
Mbadala c = 12 katika equation kwanza na kisha kutatua kwa d.
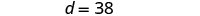
Hatua ya 6. Angalia jibu katika tatizo.	Je Devon ya umri 26 zaidi ya Cooper ya? Ndiyo, 38 ni 26 zaidi ya 12. Je, jumla ya umri wao ni 50? Ndiyo, 38 pamoja na 12 ni 50.
Hatua ya 7. Jibu swali.	Devon ni 38 na Cooper ni umri wa miaka 12.

Zoezi\(\PageIndex{8}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Ali ana umri wa miaka 12 kuliko dada yake mdogo, Jameela. Jumla ya umri wao ni 40. Kupata umri wao.

Jibu

Ali ni 26 na Jameela ni 14.

Zoezi\(\PageIndex{9}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Baba wa Jake ni umri wa 6 zaidi ya mara 3 Jake. Jumla ya umri wao ni 42. Kupata umri wao.

Jibu

Jake ni 9 na baba yake ni 33.

Zoezi\(\PageIndex{10}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Wakati Jenna alitumia dakika 10 juu ya mkufunzi elliptical na kisha alifanya mafunzo mzunguko kwa dakika 20, fitness programu yake anasema yeye kuchomwa moto 278 kalori. Alipotumia dakika 20 kwenye mkufunzi wa elliptical na mafunzo ya mzunguko wa dakika 30 alichoma kalori 473. Je, yeye huchoma kalori ngapi kwa kila dakika kwenye mkufunzi wa elliptical? Je, yeye huchoma kalori ngapi kwa kila dakika ya mafunzo ya mzunguko?

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	Tunatafuta idadi ya kalori kuchomwa kila dakika kwenye mkufunzi wa elliptical na kila dakika ya mafunzo ya mzunguko.
Hatua ya 3. Jina kile tunachotafuta.	Hebu e = idadi ya kalori kuchomwa kwa dakika juu ya mkufunzi elliptical. c= idadi ya kalori kuchomwa kwa dakika wakati mafunzo ya mzunguko
Hatua ya 4. Tafsiri katika mfumo wa equations.	Dakika 10 juu ya mafunzo ya elliptical na mzunguko kwa dakika 20, kuchomwa moto kalori 278
	Dakika 20 juu ya elliptical na dakika 30 ya mafunzo ya mzunguko kuchomwa moto kalori 473
Mfumo ni:
Hatua ya 5. Tatua mfumo wa equations.
Panua equation ya kwanza na -1 ili kupata coefficients kinyume cha e.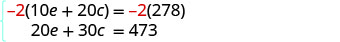
Kurahisisha na kuongeza equations. Tatua kwa c.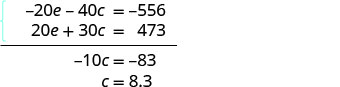
Mbadala c = 8.3 katika moja ya milinganyo ya awali ya kutatua kwa e.
Hatua ya 6. Angalia jibu katika tatizo.	Angalia hesabu peke yako.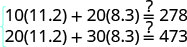
Hatua ya 7. Jibu swali.	Jenna nzito kalori 8.3 kwa dakika mzunguko mafunzo na 11.2 kalori kwa dakika wakati juu ya mkufunzi elliptical.

Zoezi\(\PageIndex{11}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Mark akaenda kwenye mazoezi na akafanya dakika 40 za yoga ya moto ya Bikram na dakika 10 za kuruka jacks. Alichoma kalori 510. Wakati mwingine alipoenda kwenye mazoezi, alifanya dakika 30 za yoga ya moto ya Bikram na dakika 20 za kuruka jacks kuchoma kalori 470. Ni kalori ngapi zilizoteketezwa kwa kila dakika ya yoga? Ni kalori ngapi zilizoteketezwa kwa kila dakika ya kuruka jacks?

Jibu

Mark kuchomwa moto kalori 11 kwa kila dakika ya yoga na kalori 7 kwa kila dakika ya kuruka jacks.

Zoezi\(\PageIndex{12}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Erin alitumia dakika 30 kwenye mashine ya kupiga makasia na dakika 20 kuinua uzito kwenye mazoezi na kuchomwa kalori 430. Wakati wa ziara yake ya pili ya mazoezi alitumia dakika 50 kwenye mashine ya kupiga makasia na dakika 10 kuinua uzito na kuchomwa kalori 600. Alichoma kalori ngapi kwa kila dakika kwenye mashine ya kupiga makasia? Alichoma kalori ngapi kwa kila dakika ya kuinua uzito?

Jibu

Erin kuchomwa moto kalori 11 kwa kila dakika kwenye mashine ya kupiga makasia na kalori 5 kwa kila dakika ya kuondoa uzito.

Kutatua Jiometri Matumizi

Tulipojifunza kuhusu Mifano ya Math, tulitatua maombi ya jiometri kwa kutumia mali ya pembetatu na rectangles. Sasa tutaweza kuongeza orodha yetu baadhi ya mali ya pembe.

Hatua za pembe mbili za ziada zinaongeza digrii 90. Hatua za pembe mbili za ziada zinaongeza digrii 180.

PEMBE ZA ZIADA NA ZIADA

Pembe mbili zinaongezea ikiwa jumla ya hatua za pembe zao ni digrii 90.

Pembe mbili ni za ziada ikiwa jumla ya hatua za pembe zao ni digrii 180.

Ikiwa pembe mbili ni za ziada, tunasema kuwa pembe moja ni inayosaidia nyingine.

Ikiwa pembe mbili ni za ziada, tunasema kuwa pembe moja ni kuongeza kwa nyingine.

Zoezi\(\PageIndex{13}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Tofauti ya pembe mbili za ziada ni digrii 26. Pata hatua za pembe.

Jibu

\(\begin{array}{ll}{\textbf {Step 1. Read}\text{ the problem. }} & {} \\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} & {\text {We are looking for the measure of each angle.}} \\ \\ {\textbf{Step 3. Name}\text{ what we are looking for.}} & {\text{Let x = the measure of the first angle.} }\\ {} & \text{y = the measure of the second angle} \\ \textbf{Step 4. Translate}\text{ into a system of equations.}& \text{The angles are complementary.} \\ & \text{x+y=90} \\ & \text{The difference of the two angles is 26 degrees.} \\ & \text{x−y=26} \\ \\ \text{The system is} & {\left\{\begin{array}{l}{x+y=90} \\ {x-y=26}\end{array}\right.} \\ \textbf{Step 5. Solve}\text{ the system of equations by elimination.} \\& \left\{\begin{array}{l}{x+y=90} \\ \underline{x-y=26}\end{array}\right. \\ & \quad2x\quad=116 \\ \text{Substitute x = 58 into the first equation.}& \begin{array}{lrll} &x&=&58 \\ &x+y&=&90 \\ &58+y&=&90 \\ &y&=&32\end{array} \\ \textbf{Step 6. Check}\text{ the answer in the problem.} & \\ 58+32=90\checkmark\\ 58-32=36\checkmark \\ \\ \textbf{Step 7. Answer}\text{ the question.} & \text{The angle measures are 58 degrees and 32 degrees.}\end{array}\)

Zoezi\(\PageIndex{14}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Tofauti ya pembe mbili za ziada ni digrii 20. Pata hatua za pembe.

Jibu

Hatua za angle ni digrii 55 na digrii 35.

Zoezi\(\PageIndex{15}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Tofauti ya pembe mbili za ziada ni digrii 80. Pata hatua za pembe.

Jibu

Hatua za angle ni digrii 5 na digrii 85.

Zoezi\(\PageIndex{16}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Pembe mbili ni za ziada. Kipimo cha angle kubwa ni digrii kumi na mbili chini ya mara tano kipimo cha angle ndogo. Pata hatua za pembe zote mbili.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	Tunatafuta kipimo cha kila angle.
Hatua ya 3. Jina kile tunachotafuta.	Hebu x= kipimo cha angle ya kwanza. y= kipimo cha angle ya pili
Hatua ya 4. Tafsiri katika mfumo wa equations.	Pembe ni ziada.
	Pembe kubwa ni kumi na mbili chini ya mara tano angle ndogo.
Mfumo ni: Hatua ya 5. Tatua mfumo wa ubadilishaji wa equations.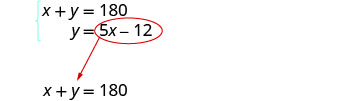
Mbadala 5 x - 12 kwa y katika equation kwanza.
Kutatua kwa x.
Mbadala 32 kwa equation ya pili, kisha kutatua kwa y.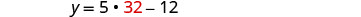
Hatua ya 6. Angalia jibu katika tatizo. \(\begin{aligned} 32+158 &=180 \checkmark \\ 5 \cdot 32-12 &=147 \checkmark \end{aligned}\)
Hatua ya 7. Jibu swali.	Hatua za angle ni 148 na 32.

Zoezi\(\PageIndex{17}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Pembe mbili ni za ziada. Kipimo cha angle kubwa ni digrii 12 zaidi ya mara tatu angle ndogo. Pata hatua za pembe.

Jibu

Hatua za angle ni digrii 42 na digrii 138.

Zoezi\(\PageIndex{18}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Pembe mbili ni za ziada. Kipimo cha angle kubwa ni 18 chini ya mara mbili kipimo cha angle ndogo. Pata hatua za pembe.

Jibu

Hatua za angle ni digrii 66 na digrii 114.

Zoezi\(\PageIndex{19}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Randall ana futi 125 za uzio ili kuzungusha sehemu ya mstatili wa mashamba yake karibu na nyumba yake. Atahitaji tu uzio kuzunguka pande tatu, kwa sababu upande wa nne utakuwa ukuta wa nyumba. Anataka urefu wa yadi yenye maboma (sambamba na ukuta wa nyumba) kuwa futi 5 zaidi ya mara nne kwa muda mrefu kama upana. Pata urefu na upana.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua unachotafuta.	Tunatafuta urefu na upana.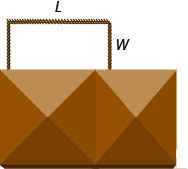
Hatua ya 3. Jina kile tunachotafuta.	Hebu L= urefu wa yadi iliyofungwa. W= upana wa yadi iliyofungwa
Hatua ya 4. Tafsiri katika mfumo wa equations.	Urefu mmoja na upana mbili sawa 125.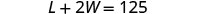
	Urefu utakuwa miguu 5 zaidi ya mara nne upana.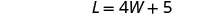
Mfumo ni: Hatua ya 5. Tatua mfumo wa equations kwa kubadilisha.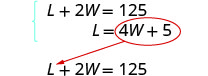
Mbadala L = 4 W + 5 katika equation ya kwanza, kisha kutatua kwa W.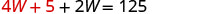
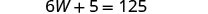
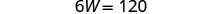
Mbadala 20 kwa W katika equation ya pili, kisha kutatua kwa L.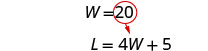
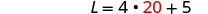
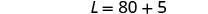
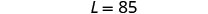
Hatua ya 6. Angalia jibu katika tatizo. \(\begin{array}{rll} 20+28+20&=&125\checkmark \\ 85 &=&4\cdot 20 + 5\checkmark\end{array}\)
Hatua ya 7. Jibu equation.	Urefu ni futi 85 na upana ni futi 20.

Zoezi\(\PageIndex{20}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Mario anataka kuweka uzio mstatili kuzunguka pool katika mashamba yake. Kwa kuwa upande mmoja ni karibu na nyumba, atahitaji tu uzio pande tatu. Kuna pande mbili ndefu na upande mmoja mfupi ni sawa na nyumba. Anahitaji futi 155 za uzio ili kuzunguka bwawa. Urefu wa upande mrefu ni miguu 10 chini ya mara mbili upana. Kupata urefu na upana wa eneo pool kuwa iliyoambatanishwa.

Jibu

Urefu ni futi 60 na upana ni futi 35.

Zoezi\(\PageIndex{21}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Alexis anataka kujenga mbwa mstatili kukimbia katika yadi yake karibu na uzio wa jirani yake. Atatumia miguu 136 ya uzio ili kufungia kabisa mbwa wa mstatili. Urefu wa mbwa kukimbia pamoja na uzio wa jirani utakuwa miguu 16 chini ya mara mbili upana. Kupata urefu na upana wa mbwa kukimbia.

Jibu

Urefu ni futi 60 na upana ni futi 38.

Kutatua maombi ya mwendo Sare

Tulitumia meza kuandaa habari katika matatizo ya mwendo sare wakati sisi ilianzisha yao mapema. Tutaendelea kutumia meza hapa. equation ya msingi ilikuwa D = rt ambapo D ni umbali alisafiri, r ni kiwango, na t ni wakati.

Mfano wetu wa kwanza wa maombi ya mwendo sare itakuwa kwa hali sawa na baadhi tumeona, lakini sasa tunaweza kutumia vigezo viwili na equations mbili.

Zoezi\(\PageIndex{22}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Joni aliondoka St Louis kwenye interstate, akiendesha gari magharibi kuelekea Denver kwa kasi ya maili 65 kwa saa. Nusu saa moja baadaye, Kelly aliondoka St Louis kwenye njia sawa na Joni, akiendesha gari maili 78 kwa saa. Itachukua muda gani Kelly kupata hadi Joni?

Jibu

Mchoro ni muhimu katika kutusaidia kutazama hali hiyo.

Tambua na kutaja kile tunachotafuta. Chati itatusaidia kuandaa data. Tunajua viwango vya wote Joni na Kelly, na hivyo tunawaingiza katika chati.
Sisi ni kuangalia kwa urefu wa muda Kelly, k, na Joni, j, itakuwa kila gari. Tangu d=r·t tunaweza kujaza safu ya Umbali.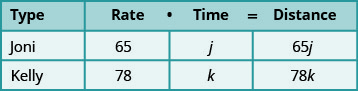
Tafsiri katika mfumo wa equations. Kufanya mfumo wa equations, tunapaswa kutambua kwamba Kelly na Joni wataendesha umbali sawa. Hivyo, 65j=78k. Pia, tangu Kelly kuondoka baadaye, muda wake utakuwa chini ya saa 1212 kuliko muda wa Joni. Hivyo, k=j-12.
Sasa tuna mfumo.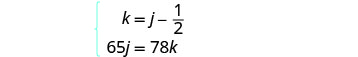
Tatua mfumo wa equations kwa kubadilisha.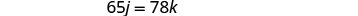
Mbadala k=j-12 katika equation ya pili, kisha kutatua kwa j.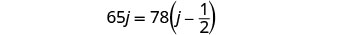
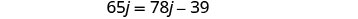
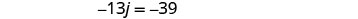
Ili kupata muda wa Kelly, mbadala j = 3 katika equation ya kwanza, kisha kutatua kwa k.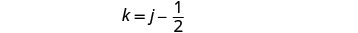
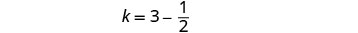
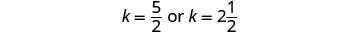
Angalia jibu katika tatizo. Kujiunga saa 3 (65 mph) = 195 maili. \(2\frac{1}{2}\)masaa Kelly (78 mph) = 195 maili. Ndiyo, watakuwa wamesafiri umbali sawa wakati wanapokutana.
Jibu swali.	Kelly atapata hadi Joni katika\(2\frac{1}{2}\) masaa. Kwa wakati huo, Joni atasafiri masaa 3.

Zoezi\(\PageIndex{23}\)

Tafsiri kwa mfumo wa equations na kisha kutatua: Mitchell kushoto Detroit juu ya interstate kuendesha gari kusini kuelekea Orlando kwa kasi ya 60 maili kwa saa. Clark aliondoka Detroit saa 1 baadaye akisafiri kwa kasi ya maili 75 kwa saa, akifuata njia sawa na Mitchell. Itachukua muda gani Clark kukamata Mitchell?

Jibu

Itachukua Clark masaa 4 kukamata Mitchell.

Zoezi\(\PageIndex{24}\)

Tafsiri kwa mfumo wa equations na kisha kutatua: Charlie aliondoka nyumba ya mama yake akisafiri kwa kasi ya wastani wa maili 36 kwa saa. Dada yake Sally aliondoka dakika 15 (saa 1/4) baadaye akisafiri njia ileile kwa kasi ya wastani ya maili 42 kwa saa. Muda gani kabla ya Sally upatikanaji wa samaki hadi Charlie?

Jibu

Itachukua\(1\frac{1}{2}\) masaa Sally kupata hadi Charlie.

Matumizi mengi ya ulimwengu halisi ya mwendo sare yanatokea kwa sababu ya madhara ya mikata-ya maji au hewa-kwa kasi halisi ya gari. Ndege za ndege za kuvuka nchi nchini Marekani kwa ujumla huchukua muda mrefu kwenda magharibi kuliko kwenda mashariki kwa sababu ya mikondo ya upepo iliyopo.

Hebu tuangalie mashua inayosafiri kwenye mto. Kulingana na njia gani mashua inakwenda, sasa ya maji ni ama kupunguza kasi au kuharakisha.

Kielelezo\(\PageIndex{1}\) na Kielelezo\(\PageIndex{2}\) kuonyesha jinsi mto sasa huathiri kasi ambayo mashua ni kweli kusafiri. Tutaweza wito kasi ya mashua katika bado maji b na kasi ya mto wa sasa c.

Katika\(\PageIndex{1}\) Kielelezo mashua ni kwenda chini ya mto, katika mwelekeo sawa na mto wa sasa. Sasa husaidia kushinikiza mashua, hivyo kasi halisi ya mashua ni kasi zaidi kuliko kasi yake katika maji bado. Kasi halisi ambayo mashua inahamia ni b + c.

Kielelezo\(\PageIndex{1}\)

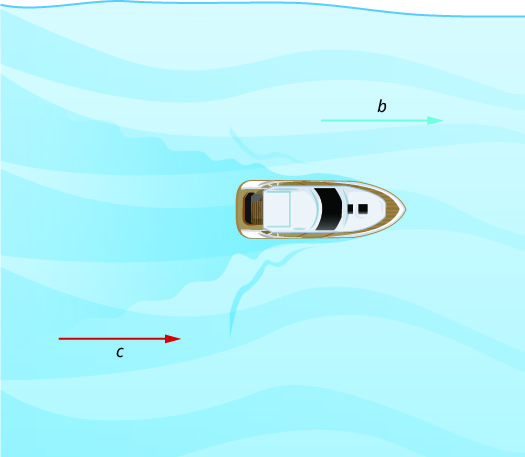
Katika Kielelezo\(\PageIndex{2}\) mashua ni kwenda juu ya mto, kinyume na mto wa sasa. Sasa inakwenda kinyume na mashua, hivyo kasi halisi ya mashua ni polepole kuliko kasi yake katika maji bado. Kasi halisi ya mashua ni b-c.

Kielelezo\(\PageIndex{2}\)

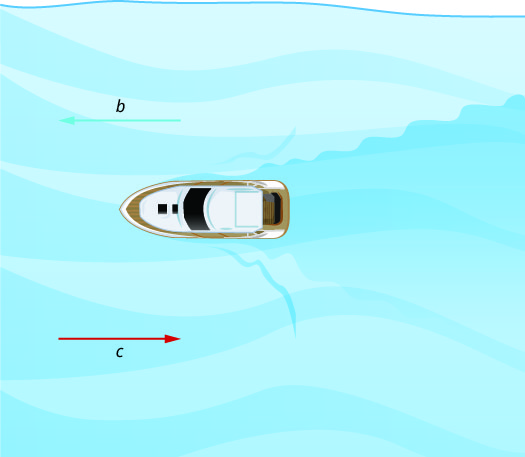
Tutaweza kuweka baadhi ya idadi ya hali hii katika Zoezi\(\PageIndex{25}\).

Zoezi\(\PageIndex{25}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Meli ya cruise ya mto ilisafiri maili 60 chini ya mto kwa masaa 4 halafu ikachukua masaa 5 meli juu ya mto kurudi gati. Kupata kasi ya meli katika maji bado na kasi ya mto wa sasa.

Jibu

Soma tatizo.

Hii ni tatizo la mwendo sare na picha itatusaidia kutazama hali hiyo.

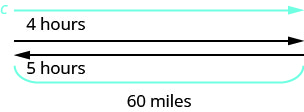
Tambua kile tunachotafuta.	Tunatafuta kasi ya meli katika maji bado na kasi ya sasa.
Jina kile tunachotafuta.	Hebu s=s= kiwango cha meli katika maji bado. c=c= kiwango cha sasa
Chati itatusaidia kuandaa habari. Meli inakwenda chini ya mto na kisha mto. Kwenda chini, sasa husaidia meli; kwa hiyo, kiwango halisi cha meli ni s + c. Kwenda juu ya mto, sasa hupunguza meli; kwa hiyo, kiwango halisi ni s - c.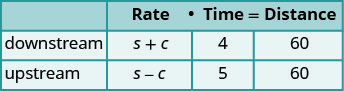
Chini ya mto inachukua masaa 4. Upstream inachukua masaa 5. Kila njia umbali ni maili 60.
Tafsiri katika mfumo wa equations. Kwa kuwa kiwango cha mara wakati ni umbali, tunaweza kuandika mfumo wa equations.
Tatua mfumo wa equations. Kusambaza kuweka equations zote mbili katika fomu ya kawaida, kisha kutatua kwa kuondoa.
Kuzidisha equation juu na 5 na equation chini na 4. Ongeza equations, kisha kutatua kwa s.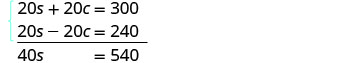
Mbadala s = 13.5 katika moja ya milinganyo ya awali.
Angalia jibu katika tatizo. Kiwango cha chini cha mto kitakuwa 13.5 + 1.5 = 15 mph. Katika masaa 4 meli ingekuwa kusafiri 15 · 4 = 60 maili. Kiwango cha mto kitakuwa 13.5 - 1.5 = 12 mph. Katika 5 masaa meli ingekuwa kusafiri 12 · 5 = 60 maili.
Jibu swali.	Kiwango cha meli ni 13.5 mph na kiwango cha sasa ni 1.5 mph.

Zoezi\(\PageIndex{26}\)

Tafsiri kwa mfumo wa milinganyo na kisha kutatua: Mississippi mto mashua cruise meli 120 maili mkondo kwa 12 masaa na kisha alichukua 10 masaa kurudi kizimbani. Kupata kasi ya mashua ya mto katika maji bado na kasi ya mto wa sasa.

Jibu

Kiwango cha mashua ni 11 mph na kiwango cha sasa ni 1 mph.

Zoezi\(\PageIndex{27}\)

Tafsiri kwa mfumo wa equations na kisha kutatua: Jason paddled mtumbwi wake 24 maili mkondo kwa saa 4. Ilichukua yake 3 masaa paddle nyuma. Kupata kasi ya mtumbwi katika maji bado na kasi ya mto wa sasa.

Jibu

Kasi ya mtumbwi ni 7 mph na kasi ya sasa ni 1 mph.

Mikondo ya upepo huathiri kasi ya ndege kwa njia sawa na mikondo ya maji huathiri kasi ya mashua. Tutaona hii katika Zoezi\(\PageIndex{28}\). Upepo wa sasa katika mwelekeo sawa na ndege inayoruka inaitwa tailwind. Upepo wa sasa unaopiga dhidi ya mwelekeo wa ndege huitwa kichwa.

Zoezi\(\PageIndex{28}\)

Tafsiri kwa mfumo wa equations na kisha kutatua:

Ndege binafsi inaweza kuruka maili 1095 katika masaa matatu na tailwind lakini tu maili 987 katika masaa matatu katika headwind. Kupata kasi ya ndege katika hewa bado na kasi ya upepo.

Jibu

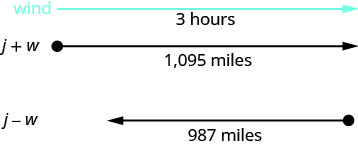
Soma tatizo.

Hii ni tatizo la mwendo sare na picha itatusaidia kutazama.

Tambua kile tunachotafuta.	Tunatafuta kasi ya ndege bado hewa na kasi ya upepo.
Jina kile tunachotafuta.	Hebu j= kasi ya ndege katika hewa bado. w= kasi ya upepo
Chati itatusaidia kuandaa habari. Ndege hufanya safari mbili-moja katika tailwind na moja katika headwind. Katika mkia, upepo husaidia ndege na hivyo kiwango ni j + w. Katika upepo wa kichwa, upepo hupungua ndege na hivyo kiwango ni j - w.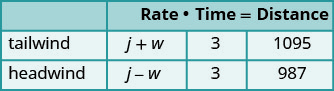
Kila safari inachukua masaa 3. Katika tailwind ndege inaruka maili 1095. Katika headwind ndege inaruka maili 987.
Tafsiri katika mfumo wa equations. Tangu kiwango cha mara wakati ni umbali, tunapata mfumo wa equations.
Tatua mfumo wa equations. Kusambaza, kisha kutatua kwa kuondoa.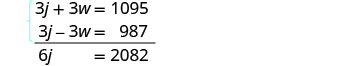
Kuongeza, na kutatua kwa j. Kubadilisha j = 347 katika moja ya equations ya awali, kisha kutatua kwa w.
Angalia jibu katika tatizo. Kwa tailwind, kiwango halisi cha ndege kitakuwa 347 + 18 = 365 mph. Katika masaa 3 ndege ingekuwa kusafiri 365 · 3 = 1095 maili. Kuingia kwenye kichwa cha kichwa, kiwango halisi cha ndege kitakuwa 347 - 18 = 329 mph. Katika masaa 3 ndege ingesafiri 329 · 3 = maili 987.
Jibu swali.	Kiwango cha ndege ni 347 mph na kiwango cha upepo ni 18 mph.

Zoezi\(\PageIndex{29}\)

Tafsiri kwa mfumo wa equations na kisha kutatua: Ndege ndogo inaweza kuruka maili 1,325 katika masaa 5 na tailwind lakini tu maili 1025 katika masaa 5 katika headwind. Kupata kasi ya ndege katika hewa bado na kasi ya upepo.

Jibu

Kasi ya ndege ni 235 mph na kasi ya upepo ni 30 mph.

Zoezi\(\PageIndex{30}\)

Tafsiri kwa mfumo wa milinganyo na kisha kutatua: Ndege ya kibiashara inaweza kuruka maili 1728 katika masaa 4 na tailwind lakini tu maili 1536 katika masaa 4 katika headwind. Kupata kasi ya ndege katika hewa bado na kasi ya upepo.

Jibu

Kasi ya ndege ni 408 mph na kasi ya upepo ni 24 mph.

faharasa

pembe za ziada

Pembe mbili zinaongezea ikiwa jumla ya hatua za pembe zao ni\(90\) digrii.

pembe za ziada

Pembe mbili ni za ziada ikiwa jumla ya hatua za pembe zao ni\(180\) digrii.