Skip to main content
Global

4.6: Pata usawa wa Mstari

  1. Last updated
  2. Save as PDF
  • Page ID
    177566

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kupata equation ya mstari kutokana na mteremko na y-intercept
    • Find equation ya mstari kutokana na mteremko na uhakika
    • Find equation ya mstari kupewa pointi mbili
    • Kupata equation ya mstari sambamba na mstari fulani
    • Kupata equation ya mstari perpendicular kwa mstari fulani
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kutatua:\(\frac{2}{3} = \frac{x}{5}\).
      Ikiwa umekosa tatizo hili, tathmini Zoezi 2.2.4.
    2. Kurahisisha:\(−\frac{2}{5}(x−15)\).
      Kama amekosa tatizo hili, mapitio Zoezi 1.10.34.

    Je, wauzaji wa mtandaoni wanajua kwamba 'unaweza pia kupenda' kipengee fulani kulingana na kitu ulichoamuru tu? Je, wanauchumi wanawezaje kujua jinsi kupanda kwa mshahara wa chini kutaathiri kiwango cha ukosefu wa ajira? Je, watafiti wa matibabu huunda madawa ya kulevya ili kulenga seli za saratani? Wahandisi wa trafiki wanaweza kutabiri athari kwa muda wako wa kubatilisha wa ongezeko au kupungua kwa bei za gesi? Yote ni hisabati.

    Wewe ni katika hatua ya kusisimua katika safari yako hisabati kama hisabati wewe ni kusoma ina maombi ya kuvutia katika ulimwengu wa kweli.

    Sayansi ya kimwili, sayansi ya jamii, na ulimwengu wa biashara ni kamili ya hali ambayo inaweza kuwa inatokana na equations linear zinazohusiana na vigezo viwili. Takwimu zinakusanywa na zimewekwa. Ikiwa pointi za data zinaonekana kuunda mstari wa moja kwa moja, equation ya mstari huo inaweza kutumika kutabiri thamani ya kutofautiana moja kulingana na thamani ya kutofautiana nyingine.

    Ili kujenga mfano wa hisabati wa uhusiano wa mstari kati ya vigezo viwili, lazima tuweze kupata equation ya mstari. Katika sehemu hii tutaangalia njia kadhaa za kuandika equation ya mstari. Njia maalum tunayotumia itaamua na habari gani tunayopewa.

    Kupata Equation ya Line Kutokana na mteremko na y -Intercept

    Tunaweza kwa urahisi kuamua mteremko na kukatiza ya mstari kama equation iliandikwa katika mteremko - intercept fomu, y = mx+b Sasa, tutafanya reverse-tutaanza na mteremko na y -intercept na matumizi yao ya kupata equation ya mstari.

    Zoezi\(\PageIndex{1}\)

    Pata usawa wa mstari na mteremko -7 na y -intercept (0, -1).

    Jibu

    Kwa kuwa tunapewa mteremko na y -intercept ya mstari, tunaweza kubadilisha maadili zinazohitajika katika fomu ya mteremko, y=mx+b.

    Jina la mteremko. .
    Jina la y -intercept. .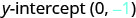
    Badala ya maadili ndani ya y=mx+b. .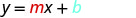
      .
      .
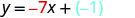
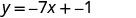
    Zoezi\(\PageIndex{2}\)

    Pata usawa wa mstari na mteremko\(\frac{2}{5}\) na y -intercept (0,4).

    Jibu

    \(y = \frac{2}{5}x + 4\)

    Zoezi\(\PageIndex{3}\)

    Pata equation ya mstari na mteremko -1 na y -intercept (0, 1-3).

    Jibu

    \(y=−x−3\)

    Wakati mwingine, mteremko na kuingilia haja ya kuamua kutoka kwenye grafu.

    Zoezi\(\PageIndex{4}\)

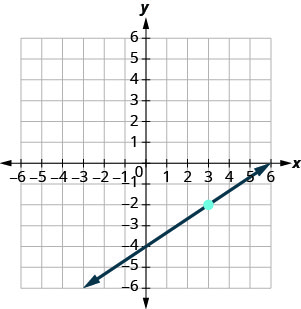
    Kupata equation ya mstari umeonyesha.

    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari unachukua mhimili wa y saa (0, hasi 4), hupita kupitia hatua iliyopangwa (3, hasi 2), na huchukua x-axis saa (4, 0).

    Jibu

    Tunahitaji kupata mteremko na y -intercept ya mstari kutoka grafu ili tuweze kubadilisha maadili zinazohitajika katika fomu ya mteremko, y=mx+by=mx+b.

    Ili kupata mteremko, tunachagua pointi mbili kwenye grafu.

    Y-intercept ni (0, -4) na grafu hupita kupitia (3, -2).

    Pata mteremko kwa kuhesabu kupanda na kukimbia. .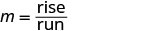
      .
    Pata y -intercept. .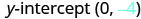
    Badala ya maadili ndani ya y=mx+b. .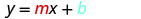
      .
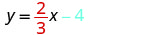
    Zoezi\(\PageIndex{5}\)

    Pata usawa wa mstari ulioonyeshwa kwenye grafu.

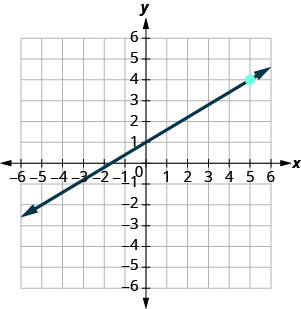
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari unachukua x-axis katika (hasi 2, 0), inakataza y mhimili katika (0, 1) na hupita kupitia hatua iliyopangwa (5, 4).

    Jibu

    \(y=\frac{3}{5}x+1\)

    Zoezi\(\PageIndex{6}\)

    Pata usawa wa mstari ulioonyeshwa kwenye grafu.

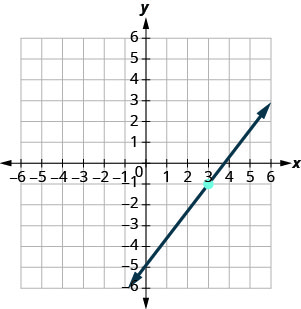
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari unachukua mhimili wa y saa (0, hasi 5), hupita kupitia hatua iliyopangwa (3, hasi 1), na inakataza x-axis saa (15 ya nne, 0).

    Jibu

    \(y=\frac{4}{3}x−5\)

    Kupata Equation ya Line Kutokana na mteremko na Point

    Kupata equation ya mstari kwa kutumia mteremko - intercept fomu ya equation kazi vizuri wakati wewe ni kupewa mteremko na y -intercept au wakati kusoma yao mbali grafu. Lakini nini kinatokea wakati una hatua nyingine badala ya y -intercept?

    Sisi ni kwenda kutumia formula mteremko hupata aina nyingine ya equation ya mstari. Tuseme tuna mstari ambayo ina mteremko mm na kwamba ina baadhi ya uhakika maalum\((x_{1}, y_{1})\) na baadhi ya hatua nyingine, ambayo sisi tu wito (x, y). Tunaweza kuandika mteremko wa mstari huu na kisha ubadilishe kwa fomu tofauti.

    \(\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x−x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the y terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)

    Fomu hii inaitwa uhakika-mteremko fomu ya equation ya mstari.

    POINT-MTEREMKO FOMU YA EQUATION YA MSTARI

    Aina ya hatua-mteremko wa equation ya mstari na mteremko mm na iliyo na uhakika\((x_{1}, y_{1})\) ni

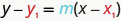
    Hakuna maandishi ya alt

    Tunaweza kutumia hatua - mteremko fomu ya equation kupata equation ya mstari wakati sisi ni kupewa mteremko na hatua moja. Kisha sisi kuandika upya equation katika mteremka-intercept fomu. Matumizi mengi ya equations linear kutumia mteremka-intercept fomu.

    Zoezi\(\PageIndex{7}\): Find an Equation of a Line Given the Slope and a Point

    Kupata equation ya mstari na mteremko\(m=\frac{2}{5}\) ambayo ina uhakika (10,3). Andika equation katika mteremka-intercept fomu.

    Jibu

    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa. Safu ya tatu ina hesabu. Katika mstari wa kwanza wa meza, kiini cha kwanza upande wa kushoto kinasoma: “Hatua ya 1. Tambua mteremko.” Nakala katika kiini cha pili inasoma: “Mteremko hutolewa.” Kiini cha tatu kina mteremko wa mstari, unaofafanuliwa kama m sawa na 2 tano.
    Katika mstari wa pili, kiini cha kwanza kinasoma: “Hatua ya 2. Tambua uhakika.” Kiini cha pili kinasoma: “Hatua hutolewa.” Kiini cha tatu kina jozi iliyoamriwa (10, 3). Subscript x subscript 1 imeandikwa juu ya 10, na superscript y subscript 1 imeandikwa juu ya 3.
    Katika mstari wa tatu, kiini cha kwanza kinasoma: “Hatua ya 3. Badilisha maadili katika fomu ya mteremko wa uhakika, y minus y subscript 1 sawa m mara x minus x subscript 1 katika mabano.” Mstari wa juu wa kiini cha pili umesalia tupu. Kiini cha tatu kina fomu ya mteremko wa uhakika imeandikwa tena: y minus y subscript 1 sawa m mara x minus x subscript 1 katika mabano. Chini hii ni fomu ya mteremko wa uhakika na 10 iliyobadilishwa kwa x subscript 1, 3 iliyobadilishwa kwa y subscript 1, na 2 tano kubadilishwa kwa m: y minus 3 sawa na mara 2 tano x bala 10 katika mabano. Mstari mmoja chini, maagizo katika kiini cha pili husema: “Rahisisha.” Katika kiini cha tatu ni y minus 3 sawa na 2 tano x minus 4.
    Katika mstari wa nne, kiini cha kwanza kinasoma: “Andika equation katika fomu ya kuingilia mteremko.” Kiini cha pili ni tupu. Katika kiini cha tatu ni y sawa na 2 tano x minus 1.

    Zoezi\(\PageIndex{8}\)

    Kupata equation ya mstari na mteremko\(m=\frac{5}{6}\) na zenye uhakika (6,3).

    Jibu

    \(y=\frac{5}{6}x−2\)

    Zoezi\(\PageIndex{9}\)

    Kupata equation ya mstari na mteremko\(m=\frac{2}{3}\) na zenye uhakika (9,2).

    Jibu

    \(y=\frac{2}{3}x−4\)

    KUPATA EQUATION YA MSTARI KUTOKANA NA MTEREMKO NA UHAKIKA.
    1. Tambua mteremko.
    2. Tambua uhakika.
    3. Weka maadili katika fomu ya mteremko wa uhakika,\(y−y_{1}=m(x−x_{1})\).
    4. Andika equation katika mteremka-intercept fomu.
    Zoezi\(\PageIndex{10}\)

    Pata usawa wa mstari na mteremko\(m=−\frac{1}{3}\) unao na uhakika (6, -4). Andika equation katika mteremka-intercept fomu.

    Jibu

    Kwa kuwa tunapewa uhakika na mteremko wa mstari, tunaweza kubadilisha maadili zinazohitajika katika fomu ya hatua-mteremko,\(y−y_{1}=m(x−x_{1})\).

    Tambua mteremko. .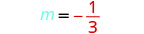
    Tambua uhakika. .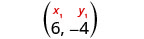
    Badala ya maadili katika\(y−y_{1}=m(x−x_{1})\). .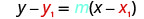
      .
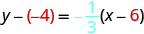
    Kurahisisha. .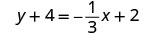
    Andika katika mteremka-kukatiza fomu. .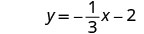
    Zoezi\(\PageIndex{11}\)

    Pata usawa wa mstari na mteremko\(m=−\frac{2}{5}\) na una uhakika (10, -5).

    Jibu

    \(y=−\frac{2}{5}x−1\)

    Zoezi\(\PageIndex{12}\)

    Pata usawa wa mstari na mteremko\(m=−\frac{3}{4}\), na una uhakika (4, -7).

    Jibu

    \(y=−\frac{3}{4}x−4\)

    Zoezi\(\PageIndex{13}\)

    Pata usawa wa mstari usio na usawa ambao una uhakika (-1,2). Andika equation katika mteremka-intercept fomu.

    Jibu

    Kila mstari wa usawa una mteremko 0. Tunaweza kubadilisha mteremko na pointi katika fomu ya hatua-mteremko,\(y−y_{1}=m(x−x_{1})\).

    Tambua mteremko. .
    Tambua uhakika. .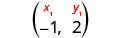
    Badala ya maadili katika\(y−y_{1}=m(x−x_{1})\). .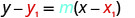
      .
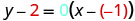
    Kurahisisha. .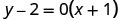
      .
      .
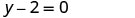
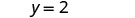
    Andika katika mteremka-kukatiza fomu. Ni katika y -fomu, lakini inaweza kuandikwa y = 0x+2.
    Je, tuliishia na fomu ya mstari usio na usawa, y=a?
    Zoezi\(\PageIndex{14}\)

    Pata usawa wa mstari usio na usawa ulio na uhakika (-3,8).

    Jibu

    y = 8

    Zoezi\(\PageIndex{15}\)

    Pata usawa wa mstari usio na usawa ulio na uhakika (-1,4).

    Jibu

    y = 4

    Kupata Equation ya Line Kutokana Pointi mbili

    Wakati data halisi ya ulimwengu inakusanywa, mfano wa mstari unaweza kuundwa kutoka kwa pointi mbili za data. Katika mfano ijayo tutaweza kuona jinsi ya kupata equation ya mstari wakati pointi mbili tu wanapewa.

    Tuna chaguzi mbili hadi sasa kwa ajili ya kutafuta equation ya mstari: mteremko - intercept au uhakika - mteremko. Kwa kuwa tutajua pointi mbili, itakuwa na maana zaidi kutumia fomu ya mteremko wa uhakika.

    Lakini basi tunahitaji mteremko. Je, tunaweza kupata mteremko na pointi mbili tu? Ndiyo. Kisha, mara moja tuna mteremko, tunaweza kutumia na moja ya pointi kutokana na kupata equation.

    Zoezi\(\PageIndex{16}\): Find an Equation of a Line Given Two Points

    Kupata equation ya mstari ambayo ina pointi (5,4) na (3,6). Andika equation katika mteremka-intercept fomu.

    Jibu

    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa. Safu ya tatu ina hesabu. Katika mstari wa kwanza wa meza, kiini cha kwanza upande wa kushoto kinasoma: “Hatua ya 1. Pata mteremko ukitumia pointi zilizotolewa.” Nakala katika kiini cha pili inasoma: “Ili kutumia fomu ya mteremko wa uhakika, tunapata kwanza mteremko.” Kiini cha tatu kina mteremko wa fomu ya mstari: m sawa na y superscript 2 minus y superscript 1 imegawanywa na x superscript 2 minus x superscript 1. Chini ya hii ni m sawa na 6 minus 4 imegawanywa na 3 minus 5. Chini hii ni m sawa na 2 imegawanywa na hasi 2. Chini hii ni m sawa na hasi 1.Katika mstari wa pili, kiini cha kwanza kinasoma: “Hatua ya 2. Chagua hatua moja.” Kiini cha pili kinasoma: “Chagua hatua yoyote.” Kiini cha tatu kina jozi iliyoamriwa (5, 4) na superscript x subscript 1 juu ya 5 na superscript y subscript 1 juu ya 4.Katika mstari wa tatu, kiini cha kwanza kinasoma: “Hatua ya 3. Badilisha maadili katika fomu ya mteremko wa uhakika, y minus y subscript 1 sawa m mara x minus x subscript 1 katika mabano.” Mstari wa juu wa kiini cha pili umesalia tupu. Kiini cha tatu kina fomu ya mteremko wa uhakika, y minus y subscript 1 sawa na m mara x minus x subscript 1 katika mabano. Chini hii ni fomu ya mteremko wa hatua na 5 iliyobadilishwa kwa x subscript 1, 4 iliyobadilishwa kwa y subscript 1, na hasi 1 kubadilishwa kwa m: y minus 4 sawa na hasi mara 1 x bala 5 katika mabano. Chini hii ni y minus 4 sawa na hasi x pamoja 5.Katika mstari wa nne, kiini cha kwanza kinasoma: “Hatua ya 4. Andika equation katika fomu ya mteremko.” Kiini cha pili ni tupu. Kiini cha tatu kina y sawa na hasi x pamoja na 9.

    Tumia hatua (3,6) na uone kwamba unapata equation sawa.

    Zoezi\(\PageIndex{17}\)

    Kupata equation ya mstari zenye pointi (3,1) na (5,6).

    Jibu

    \(y=\frac{5}{2}x−\frac{13}{2}\)

    Zoezi\(\PageIndex{18}\)

    Kupata equation ya mstari zenye pointi (1,4) na (6,2).

    Jibu

    \(y=−\frac{2}{5}x+\frac{22}{5}\)

    KUPATA EQUATION YA MSTARI KUPEWA POINTI MBILI.
    1. Pata mteremko kwa kutumia pointi zilizopewa.
    2. Chagua hatua moja.
    3. Weka maadili katika fomu ya mteremko wa uhakika,\(y−y_{1}=m(x−x_{1})\).
    4. Andika equation katika mteremka-intercept fomu.
    Zoezi\(\PageIndex{19}\)

    Pata usawa wa mstari unao na pointi (-3, -1) na (2, -1). Andika equation katika mteremka-intercept fomu.

    Jibu

    Kwa kuwa tuna pointi mbili, tutapata equation ya mstari kwa kutumia hatua - mteremko fomu. Hatua ya kwanza itakuwa kupata mteremko.

    Pata mteremko wa mstari kupitia (-3, -1) na (2, -2). .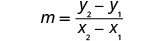
      .
      .
      .
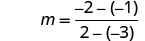
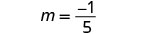
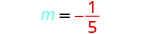
    Chagua hatua yoyote. .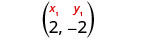
    Badala ya maadili katika\(y−y_{1}=m(x−x_{1})\). .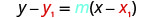
      .
      .
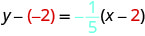
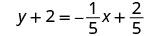
    Andika katika mteremka-kukatiza fomu. .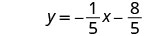
    Zoezi\(\PageIndex{20}\)

    Pata usawa wa mstari ulio na pointi (-1, -4) na (1, 1-3).

    Jibu

    \(y=\frac{1}{3}x−\frac{10}{3}\)

    Zoezi\(\PageIndex{21}\)

    Pata usawa wa mstari ulio na pointi (-4, 1-3) na (1, -5).

    Jibu

    \(y=−\frac{2}{5}x−\frac{23}{5}\)

    Zoezi\(\PageIndex{22}\)

    Pata equation ya mstari unao na pointi (-2,4) na (-1, -1, -3). Andika equation katika mteremka-intercept fomu.

    Jibu

    Tena, hatua ya kwanza itakuwa kupata mteremko.

    \(\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}\)

    Hii inatuambia ni mstari wa wima. Vipengele vyetu vyote vina x -kuratibu ya -1. Hivyo equation yetu ya mstari ni x=-1. Kwa kuwa hakuna yy, hatuwezi kuiandika katika fomu ya mteremka-kukatiza.

    Unaweza kutaka mchoro grafu kwa kutumia pointi mbili zilizopewa. Je! Grafu inakubaliana na hitimisho letu kwamba hii ni mstari wa wima?

    Zoezi\(\PageIndex{23}\)

    Pata usawa wa mstari ulio na pointi (5,1) na (5, -4).

    Jibu

    x = 5

    Zoezi\(\PageIndex{24}\)

    Pata usawa wa mstari ulio na pointi (-4,4) na (-4,3).

    Jibu

    x=-4

    Tumeona kwamba tunaweza kutumia ama mteremko - intercept fomu au uhakika-mteremko fomu kupata equation ya mstari. Fomu ipi tunayotumia itategemea habari tunayopewa. Hii ni muhtasari katika Jedwali\(\PageIndex{1}\).

    Kuandika Ulinganisho wa Mstari
    Ikiwa imetolewa: Tumia: Fomu:
    Mteremko na y -intercept mteremko—kukatiza y=mx+b
    Mteremko na uhakika uhakika-mteremko \(y−y_{1}=m(x−x_{1})\)
    Pointi mbili uhakika-mteremko \(y−y_{1}=m(x−x_{1})\)
    Jedwali\(\PageIndex{1}\)

    Pata Equation ya Mstari Sambamba na Line Iliyopewa

    Tuseme tunahitaji kupata equation ya mstari kwamba hupita kwa njia ya hatua maalum na ni sambamba na mstari fulani. Tunaweza kutumia ukweli kwamba mistari sambamba ina mteremko huo. Hivyo tutakuwa na uhakika na mteremko - tu kile tunahitaji kutumia hatua - mteremko equation.

    Kwanza hebu tuangalie hii graphically.

    Grafu inaonyesha grafu ya y=2x-3. Tunataka graph mstari sambamba na mstari huu na kupita kupitia hatua (-2,1).

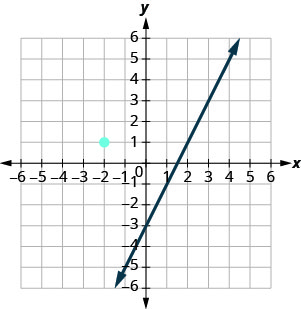
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari ambao equation ni y sawa na 2x minus 3 inachukua y axis katika (0, hasi 3) na inakataza x-axis saa (3 halves, 0). Mahali pengine kwenye grafu, hatua (hasi 2, 1) imepangwa.
    Kielelezo\(\PageIndex{1}\)

    Tunajua kwamba mistari sambamba ina mteremko huo. Hivyo mstari wa pili utakuwa na mteremko sawa na y=2x-3. Mteremko huo ni\(m_{\|} = 2\). Tutatumia nukuu\(m_{\|}\) kuwakilisha mteremko wa mstari sambamba na mstari na mteremko m (Angalia kwamba subscript inaonekana kama mistari miwili sambamba.)

    Mstari wa pili utapita kupitia (-2,1) na kuwa na m=2. Ili kuchora mstari, tunaanza saa (-2,1) na tuhesabu kupanda na kukimbia. Na m=2 (au\(m=\frac{2}{1}\)), tunahesabu kupanda 2 na kukimbia 1. Tunapata mstari.

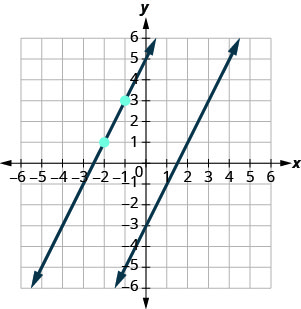
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari ambao equation ni y sawa na 2x minus 3 inachukua y axis katika (0, hasi 3) na inakataza x-axis saa (3 halves, 0). Vipengele (hasi 2, 1) na (hasi 1, 3) vinapangwa. Mstari wa pili, sambamba na wa kwanza, huchukua x-axis katika (hasi 5 halves, 0), hupita kupitia pointi (hasi 2, 1) na (hasi 1, 3), na huchukua y-axis saa (0, 5).
    Kielelezo\(\PageIndex{2}\)

    Je, mistari inaonekana sambamba? Je, mstari wa pili unapita kupitia (-2,1)?

    Sasa, hebu tuone jinsi ya kufanya hivyo kwa usahihi.

    Tunaweza kutumia ama mteremko - intercept fomu au fomu ya uhakika-mteremko kupata equation ya mstari. Hapa tunajua hatua moja na tunaweza kupata mteremko. Kwa hiyo tutatumia fomu ya mteremko wa uhakika.

    Zoezi\(\PageIndex{25}\): How to Find an Equation of a Line Parallel to a Given Line

    Pata equation ya mstari sambamba na y=2x-1 ambayo ina uhakika (-2,1). Andika equation katika mteremka-intercept fomu.

    Jibu

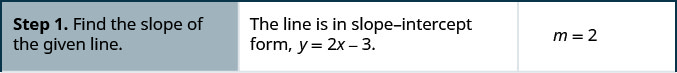
    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa. Safu ya tatu ina hesabu. Katika mstari wa kwanza wa meza, kiini cha kwanza upande wa kushoto kinasoma: “Hatua ya 1. Pata mteremko wa mstari uliotolewa.” Kiini cha pili kinasoma: “Mstari ni katika fomu ya kupinga mteremko. y ni sawa na 2x minus 3.” Kiini cha tatu kina mteremko wa mstari, hufafanuliwa kama m sawa na 2.Katika mstari wa pili, kiini cha kwanza kinasoma: “Hatua ya 2. Pata mteremko wa mstari sambamba.” Kiini cha pili kinasoma “Mstari sambamba una mteremko huo.” Kiini cha tatu kina mteremko wa mstari sambamba, hufafanuliwa kama m sambamba sawa na 2.Katika mstari wa tatu, kiini cha kwanza kinasoma “Hatua ya 3. Tambua uhakika.” Kiini cha pili kinasoma “Hatua iliyotolewa ni (hasi 2, 1).” Kiini cha tatu kina jozi iliyoamriwa (hasi 2, 1) na superscript x subscript 1 juu ya hasi 2 na superscript y subscript 1 juu ya 1.Katika mstari wa nne, kiini cha kwanza kinasoma “Hatua ya 4. Badilisha maadili katika fomu ya mteremko wa uhakika, y minus y subscript 1 sawa m mara x minus x subscript 1 katika mabano.” Juu ya kiini cha pili ni tupu. Kiini cha tatu kina fomu ya mteremko wa uhakika, y minus y subscript 1 sawa na m mara x minus x subscript 1 katika mabano. Chini hii ni fomu na hasi 2 iliyobadilishwa kwa x subscript 1, 1 iliyobadilishwa kwa y subscript 1, na 2 kubadilishwa kwa m: y minus 1 sawa mara 2 x bala hasi 2 katika mabano. Mstari mmoja chini, maandishi katika kiini cha pili inasema “Rahisisha.” Safu ya haki ina y minus 1 sawa na mara 2 x pamoja na 2. Chini ya hii ni y minus 1 sawa 2x pamoja 4.Katika mstari wa tano, kiini cha kwanza kinasema “Hatua ya 5. Andika equation katika fomu ya mteremko.” Kiini cha pili ni tupu. Kiini cha tatu kina y sawa na 2x pamoja na 5.

    Je, equation hii ina maana? Je, ni y -intercept ya mstari? Mteremko ni nini?

    Zoezi\(\PageIndex{26}\)

    Kupata equation ya mstari sambamba na mstari y = 3x+1 ambayo ina uhakika (4,2). Andika equation katika mteremka-intercept fomu.

    Jibu

    y=3x-10

    Zoezi\(\PageIndex{27}\)

    Kupata equation ya mstari sambamba na mstari\(y=\frac{1}{2}x−3\) ambayo ina uhakika (6,4).

    Jibu

    \(y=\frac{1}{2}x+1\)

    PATA EQUATION YA MSTARI SAMBAMBA NA MSTARI FULANI.
    1. Pata mteremko wa mstari uliopewa.
    2. Pata mteremko wa mstari sambamba.
    3. Tambua uhakika.
    4. Badilisha maadili katika fomu ya hatua-mteremko,\(y−y_{1}=m(x−x_{1})\).
    5. Andika equation katika mteremka-intercept fomu.

    Kupata Equation ya Line Perpendicular kwa Line Kutokana

    Sasa, hebu fikiria mistari ya perpendicular. Tuseme tunahitaji kupata mstari unaopita kupitia hatua maalum na ambayo ni perpendicular kwa mstari fulani. Tunaweza kutumia ukweli kwamba mistari ya perpendicular ina mteremko ambao ni hasi kurudi. Sisi tena kutumia uhakika - mteremko equation, kama tulivyofanya na mistari sambamba.

    Grafu inaonyesha grafu ya y=2x-3. Sasa, tunataka grafu mstari perpendicular kwa mstari huu na kupita kupitia (-2,1).

    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari ambao equation ni y sawa na 2x minus 3 inachukua y axis katika (0, hasi 3) na inakataza x-axis saa (3 halves, 0). Mahali pengine kwenye grafu, hatua (hasi 2, 1) imepangwa.
    Kielelezo\(\PageIndex{3}\)

    Tunajua kwamba mistari ya perpendicular ina mteremko ambao ni hasi usawa. Tutatumia nukuu\(m_{\perp}\) kuwakilisha mteremko wa mstari perpendicular kwa mstari na mteremko m. (Angalia kwamba subscript\(_{\perp}\) inaonekana kama pembe za kulia zilizofanywa na mistari miwili perpendicular.)

    \[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\]

    Sasa tunajua mstari wa perpendicular utapita kupitia (-2,1) na\(m_{\perp}=−\frac{1}{2}\).

    Ili kuchora mstari, tutaanza saa (-2,1) na tuhesabu kupanda -1 na kukimbia 2. Kisha sisi kuteka mstari.

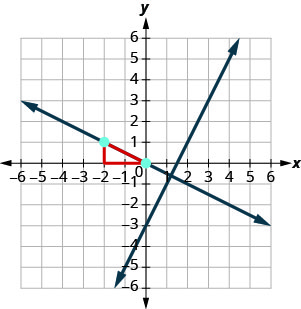
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari ambao equation ni y sawa na 2x minus 3 inachukua y axis katika (0, hasi 3) na inakataza x-axis saa (3 halves, 0). Mahali pengine, hatua (hasi 2, 1) imepangwa. Mstari mwingine perpendicular kwa mstari wa kwanza hupita kupitia hatua (hasi 2, 1) na inakataza x na y-axes saa (0, 0). Mstari mwembamba na mshale unaendelea kushoto kutoka (0, 0) hadi (hasi 2, 0), kisha huongeza na kuishia saa (hasi 2, 1), kutengeneza pembetatu sahihi na mstari wa pili kama hypotenuse.
    Kielelezo\(\PageIndex{4}\)

    Je, mistari inaonekana perpendicular? Je, mstari wa pili unapita kupitia (-2,1)?

    Sasa, hebu tuone jinsi ya kufanya hivyo kwa usahihi. Tunaweza kutumia ama mteremko - intercept fomu au fomu ya uhakika-mteremko kupata equation ya mstari. Katika mfano huu tunajua hatua moja, na tunaweza kupata mteremko, hivyo tutatumia fomu ya hatua-mteremko.

    Zoezi\(\PageIndex{28}\)

    Pata equation ya mstari perpendicular kwa y=2x-1 ambayo ina uhakika (-2,1). Andika equation katika mteremka-intercept fomu.

    Jibu

    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa. Safu ya tatu ina hesabu. Katika mstari wa kwanza wa meza, kiini cha kwanza upande wa kushoto kinasoma: “Hatua ya 1. Pata mteremko wa mstari uliotolewa.” Kiini cha pili kinasoma: “Mstari ni katika fomu ya kupinga mteremko. y ni sawa na 2x minus 3.” Kiini cha tatu kina mteremko wa mstari, hufafanuliwa kama m sawa na 2.
    Katika mstari wa pili, kiini cha kwanza kinasoma “Hatua ya 2. Pata mteremko wa mstari wa perpendicular.” Kiini cha pili kinasoma “Mteremko wa mistari ya perpendicular ni usawa hasi.” Kiini cha tatu kina m sawa na nusu moja hasi.
    Katika mstari wa tatu, kiini cha kwanza kinasoma “Hatua ya 3. Tambua uhakika.” Kiini cha pili kinasoma “Hatua iliyotolewa ni (hasi 2, 1).” Kiini cha tatu kina jozi iliyoamriwa (hasi 2, 1) na superscript x subscript 1 juu ya hasi 2 na superscript y subscript 1 juu ya 1.
    Katika mstari wa nne, kiini cha kwanza kinasema “Hatua ya 4. Badilisha maadili katika fomu ya mteremko wa uhakika.” Kiini cha pili kinasema, “Kurahisisha.” Kiini cha tatu kinaonyesha kazi hii, kuishia na y - 1 = - 1/2 x - 1.
    Katika mstari wa tano, kiini cha kwanza kinasema “Hatua ya 5. Andika equation katika fomu ya mteremko.” Kiini cha pili ni tupu. Kiini cha tatu kina y sawa na hasi 1 nusu x.

    Zoezi\(\PageIndex{29}\)

    Pata equation ya mstari perpendicular kwa mstari y = 3x+1 ambayo ina uhakika (4,2). Andika equation katika mteremka-intercept fomu.

    Jibu

    \(y=−\frac{1}{3}x+\frac{10}{3}\)

    Zoezi\(\PageIndex{30}\)

    Pata equation ya mstari perpendicular kwa mstari\(y=\frac{1}{2}x−3\) ambayo ina uhakika (6,4).

    Jibu

    y=-2x+16

    PATA EQUATION YA MSTARI PERPENDICULAR KWA MSTARI FULANI.
    1. Pata mteremko wa mstari uliopewa.
    2. Pata mteremko wa mstari wa perpendicular.
    3. Tambua uhakika.
    4. Badilisha maadili katika fomu ya hatua-mteremko,\(y−y_{1}=m(x−x_{1})\).
    5. Andika equation katika mteremka-intercept fomu.
    Zoezi\(\PageIndex{31}\)

    Pata equation ya mstari perpendicular kwa x=5 ambayo ina uhakika (3, ї2). Andika equation katika mteremka-intercept fomu.

    Jibu

    Tena, kwa kuwa tunajua hatua moja, chaguo la hatua-mteremko linaonekana kuwa na matumaini zaidi kuliko chaguo la mteremko. Tunahitaji mteremko kutumia fomu hii, na tunajua mstari mpya utakuwa perpendicular kwa x=5. Mstari huu ni wima, hivyo perpendicular yake itakuwa usawa. Hii inatuambia\(m_{\perp}=0\).

    \(\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}\)

    Mchoro grafu ya mistari yote. Je, wanaonekana kuwa perpendicular?

    Zoezi\(\PageIndex{32}\)

    Kupata equation ya mstari kwamba ni perpendicular kwa mstari x=4 ambayo ina uhakika (4, -5). Andika equation katika mteremka-intercept fomu.

    Jibu

    y=-5

    Zoezi\(\PageIndex{33}\)

    Kupata equation ya mstari kwamba ni perpendicular kwa mstari x=2 ambayo ina uhakika (2, -1). Andika equation katika mteremka-intercept fomu.

    Jibu

    y=-1

    Katika Zoezi\(\PageIndex{31}\), sisi kutumika uhakika-mteremko fomu kupata equation. Tungeweza kutazama hili kwa njia tofauti.

    Tunataka kupata mstari kwamba ni perpendicular kwa x=5 ambayo ina uhakika (3, -1). Grafu inatuonyesha mstari x=5 na uhakika (3, -1).

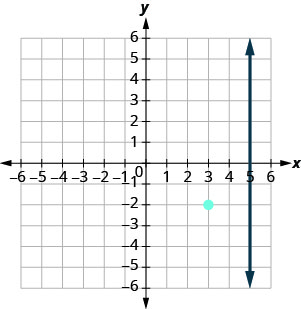
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari ambao equation ni x sawa na 5 inachukua x-axis saa (5, 0) na inaendesha sambamba na y-axis. Mahali pengine kwenye grafu, hatua (3, hasi 2) imepangwa.
    Kielelezo\(\PageIndex{5}\)

    Tunajua kila mstari perpendicular kwa mstari wima ni usawa, hivyo sisi mchoro mstari usawa kupitia (3, -1).

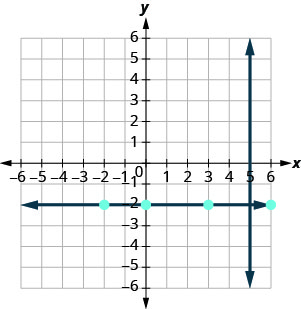
    Grafu inaonyesha ndege ya kuratibu x y. Ya x na y-axes kila kukimbia kutoka hasi 7 hadi 7. Mstari ambao equation ni x sawa na 5 inachukua x-axis saa (5, 0) na inaendesha sambamba na y-axis. Mahali pengine kwenye grafu, pointi (hasi 2, hasi 2), (0, hasi 2), (3, hasi 2), na (6, hasi 2) zimepangwa. Mstari unaozingatia mstari uliopita unapita kupitia pointi hizo na huendesha sambamba na x-axis.
    Kielelezo\(\PageIndex{6}\)

    Je, mistari inaonekana perpendicular?

    Kama sisi kuangalia pointi chache juu ya mstari huu usawa, tunaona wote wana y -kuratibu ya -1. Hivyo, equation ya mstari perpendicular kwa mstari wima x=5 ni y=-1 2.

    Zoezi\(\PageIndex{34}\)

    Pata equation ya mstari unaofanana na y=-4 ambayo ina uhakika (-4,2). Andika equation katika mteremka-intercept fomu.

    Jibu

    Mstari y=-4 ni mstari usio na usawa. Mstari wowote unaozingatia lazima uwe wima, kwa fomu x=a.Kwa kuwa mstari wa perpendicular ni wima na hupita kupitia (-4,2), kila hatua juu yake ina x -kuratibu ya -4. Ulinganisho wa mstari wa perpendicular ni x=4-7. Unaweza kutaka mchoro mistari. Je, wanaonekana perpendicular?

    Zoezi\(\PageIndex{35}\)

    Pata equation ya mstari unaozingatia mstari y =1 ambayo ina uhakika (-5,1). Andika equation katika mteremka-intercept fomu.

    Jibu

    x=-5

    Zoezi\(\PageIndex{36}\)

    Pata equation ya mstari unaozingatia mstari y =-5 ambao una uhakika (-4, -5).

    Jibu

    x=-4

    Kumbuka

    Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na kutafuta usawa wa mstari.

    Dhana muhimu

    • Kupata Equation ya Line Kutokana na mteremko na Point
      1. Tambua mteremko.
      2. Tambua uhakika.
      3. Weka maadili katika fomu ya mteremko wa uhakika,\(y−y_{1}=m(x−x_{1})\).
      4. Andika equation katika fomu ya mteremka-intercept.
    • Kupata Equation ya Mstari Kutolewa Pointi mbili
      1. Pata mteremko kwa kutumia pointi zilizopewa.
      2. Chagua hatua moja.
      3. Weka maadili katika fomu ya mteremko wa uhakika,\(y−y_{1}=m(x−x_{1})\).
      4. Andika equation katika fomu ya mteremka-intercept.
    • Kuandika na Equation ya Line
      • Kama kupewa mteremko na\(y\) -intercept, kutumia mteremka-intercept fomu\(y=mx+b\).
      • Kama kupewa mteremko na uhakika, kutumia uhakika-mteremko fomu\(y−y_{1}=m(x−x_{1})\).
      • Ikiwa imepewa pointi mbili, tumia fomu ya mteremko\(y−y_{1}=m(x−x_{1})\).
    • Kupata Ulinganisho wa Mstari Sambamba na Mstari uliotolewa
      1. Pata mteremko wa mstari uliopewa.
      2. Pata mteremko wa mstari sambamba.
      3. Tambua uhakika.
      4. Weka maadili katika fomu ya mteremko wa uhakika,\(y−y_{1}=m(x−x_{1})\).
      5. Andika equation katika fomu ya mteremka-intercept.
    • Kupata Equation ya Line Perpendicular kwa Line Kupewa
      1. Pata mteremko wa mstari uliopewa.
      2. Pata mteremko wa mstari wa perpendicular.
      3. Tambua uhakika.
      4. Weka maadili katika fomu ya mteremko wa uhakika,\(y−y_{1}=m(x−x_{1})\).
      5. Andika equation katika fomu ya mteremka-intercept.

    faharasa

    fomu ya hatua-mteremko
    Aina ya hatua-mteremko wa equation ya mstari na mteremko mm na zenye uhakika\(\left(x_{1}, y_{1}\right)\) ni\(y-y_{1}=m\left(x-x_{1}\right)\).