4.1: Tumia Mfumo wa Kuratibu wa Rectangular
- Page ID
- 177623
Mwishoni mwa sehemu hii, utaweza:
- Panda pointi katika mfumo wa kuratibu mstatili
- Thibitisha ufumbuzi wa equation katika vigezo viwili
- Jaza meza ya ufumbuzi wa equation linear
- Kupata ufumbuzi wa equation linear katika vigezo mbili
Kabla ya kuanza, fanya jaribio hili la utayari.
- Tathmini\(x+3\) lini\(x=−1\).
Kama amekosa tatizo hili, kupitia Zoezi 1.5.25. - Tathmini\(2x−5y\) lini\(x=3\) na y=-2.
Ikiwa umekosa tatizo hili, tathmini Zoezi 1.5.28. - Tatua kwa y:\(40−4y=20\)
Ikiwa umekosa tatizo hili, kagua Zoezi 2.3.1.
Plot Pointi kwenye mfumo wa Kuratibu Rectangular
Kama vile ramani zinazotumia mfumo wa gridi kutambua maeneo, mfumo wa gridi hutumika katika algebra kuonyesha uhusiano kati ya vigezo viwili katika mfumo wa kuratibu mstatili. Mfumo wa kuratibu mstatili pia huitwa xy -plane au 'kuratibu ndege'.
Mstari wa nambari ya usawa huitwa x-axis. Mstari wa nambari ya wima huitwa y-axis. Mhimili wa x na y -axis pamoja huunda mfumo wa kuratibu mstatili. Axes hizi hugawanya ndege katika mikoa minne, inayoitwa quadrants. Quadrants zinatambuliwa na namba za Kirumi, kuanzia upande wa juu wa kulia na kuendelea kinyume chake. Angalia Kielelezo\(\PageIndex{1}\).
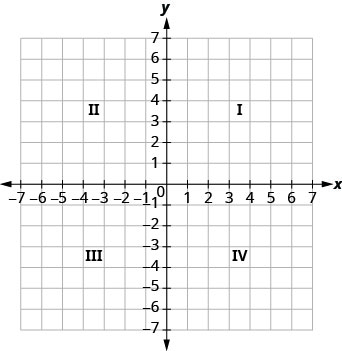
Katika mfumo wa kuratibu mstatili, kila hatua inawakilishwa na jozi iliyoamriwa. Nambari ya kwanza katika jozi iliyoamriwa ni x -kuratibu ya uhakika, na namba ya pili ni y -kuratibu ya uhakika.
Jozi iliyoamriwa, (x, y) (x, y), inatoa kuratibu ya uhakika katika mfumo wa kuratibu mstatili.
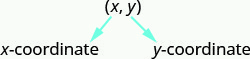
Nambari ya kwanza ni x -kuratibu.
Nambari ya pili ni y -kuratibu.
Maneno 'kuamuru jozi' inamaanisha utaratibu ni muhimu. Je, ni jozi iliyoamriwa ya uhakika ambapo axes huvuka? Katika hatua hiyo kuratibu zote mbili ni sifuri, hivyo jozi yake kuamuru ni\((0,0)\). Hatua\((0,0)\) ina jina maalum. Inaitwa asili.
Hatua\((0,0)\) inaitwa asili. Ni hatua ambapo x -axis na y -axis intersect.
Sisi kutumia kuratibu Machapisho uhakika juu ya xy -plane. Hebu tufanye njama\((1,3)\) kama mfano. Kwanza, tafuta 1 kwenye mhimili wa x na mchoro mdogo mstari wa wima kupitia x=1x=1. Kisha, tafuta 3 kwenye y -axis na mchoro mstari usio na usawa kupitia y = 3y=3. Sasa, kupata uhakika ambapo mistari hizi mbili kukutana - kwamba ni hatua na kuratibu\((1,3)\).
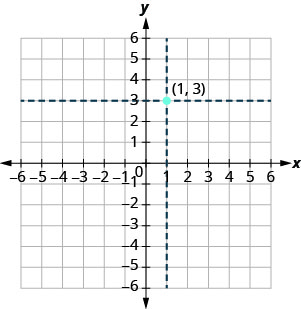
Angalia kwamba mstari wa wima kupitia\(x=1\) na mstari usio na usawa kupitia\(y=3\) sio sehemu ya grafu. Tulitumia tu kutusaidia kupata uhakika\((1,3)\).
Panda kila hatua katika mfumo wa kuratibu mstatili na kutambua quadrant ambayo hatua iko:
- (-5,4)
- (1-3, -4)
- (2, 1-3)
- (-2,3)
- \((3, \frac{5}{2})\)
- Jibu
-
Nambari ya kwanza ya jozi ya kuratibu ni kuratibu x, na namba ya pili ni y -kuratibu.
- Tangu x=-5, hatua ni upande wa kushoto wa y -axis. Pia, tangu y = 4, hatua ni juu ya x -axis. Hatua (-5,4) iko katika Quadrant II.
- Tangu x=—3, hatua ni upande wa kushoto wa y -axis. Pia, tangu y = -4, hatua ni chini ya x -axis. Neno (-3, -4) liko katika Quadrant III.
- Tangu x=2, hatua ni ya haki ya y -axis. Tangu y=—3, hatua iko chini ya x -axis. Hatua (2, 1-3) iko katika Quadrant lV.
- Tangu x=-1, hatua ni upande wa kushoto wa y -axis. Tangu y=3, hatua ni juu ya x -axis. Neno (-2,3) liko katika Quadrant II.
- Tangu x=3, hatua ni ya haki ya y -axis. Tangu\(y = \frac{5}{2}\), hatua ni juu ya x -axis. (Inaweza kuwa na manufaa kuandika\(\frac{5}{2}\) kama nambari iliyochanganywa au decimal.) Hatua\((3, \frac{5}{2})\) ni katika Quadrant I.
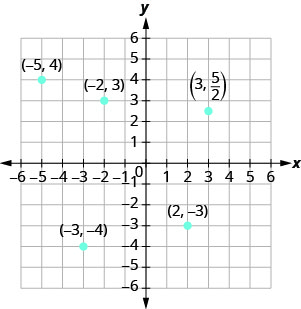
Kielelezo\(\PageIndex{4}\)
Panda kila hatua katika mfumo wa kuratibu mstatili na kutambua quadrant ambayo hatua iko:
- (-2,1)
- (1-3, -1)
- (4, -4)
- (-4,4)
- \((-4, \frac{3}{2})\)
- Jibu
-
Panda kila hatua katika mfumo wa kuratibu mstatili na kutambua quadrant ambayo hatua iko:
- (-4,1)
- (-2,3)
- (2, -5)
- (-2,5)
- \((-3, \frac{5}{2})\)
- Jibu
-
Je! Ishara zinaathirije eneo la pointi? Huenda umeona baadhi ya ruwaza kama ulivyoweka pointi katika mfano uliopita.
Kwa uhakika katika Kielelezo\(\PageIndex{4}\) katika Quadrant IV, unaona nini kuhusu ishara za kuratibu? Nini kuhusu ishara za kuratibu za pointi katika quadrant ya tatu? Quadrant ya pili? Quadrant ya kwanza?
Je, unaweza kuwaambia tu kwa kuangalia kuratibu ambazo quadrant uhakika (-2,5) iko? Katika roboduara ipi (2, -5) iko?
Tunaweza muhtasari mifumo ya ishara ya quadrants kwa njia hii.
\[\begin{array}{ccc}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\]
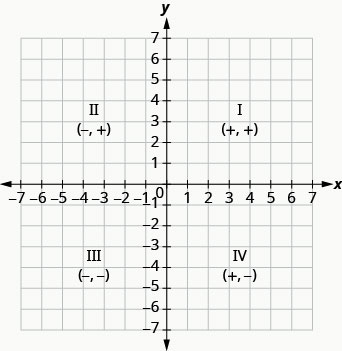
Nini kama kuratibu moja ni sifuri kama inavyoonekana katika Kielelezo\(\PageIndex{6}\)? Ambapo ni uhakika (0,4) iko wapi? Ambapo ni uhakika (-2,0) iko wapi?
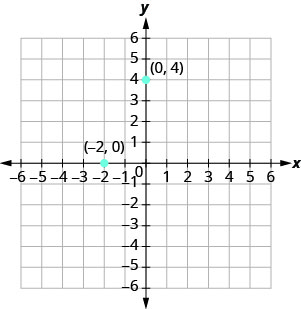
Hatua (0,4) iko kwenye y -axis na uhakika (-2,0) iko kwenye x -axis.
Pointi na y -kuratibu sawa na 0 ni juu ya x -axis, na kuwa na kuratibu (a,0).
Pointi na x -kuratibu sawa na 0 ni juu ya y -axis, na kuwa na kuratibu (0, b).
Panda kila hatua:
- (0,5)
- (4,0)
- (-3,0)
- (0,0)
- (0, -1)
- Jibu
-
- Tangu x=0, hatua ambayo kuratibu ni (0,5) iko kwenye y -axis.
- Tangu y=0, hatua ambayo kuratibu ni (4,0) iko kwenye x -axis.
- Tangu y=0, hatua ambayo kuratibu ni (-3,0) iko kwenye x -axis.
- Tangu x=0 na y=0, hatua ambayo kuratibu ni (0,0) ni asili.
- Tangu x=0, hatua ambayo kuratibu ni (0, -1) iko kwenye y -axis.
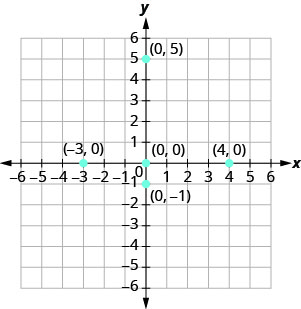
Kielelezo\(\PageIndex{7}\)
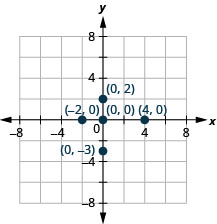
Panda kila hatua:
- (4,0)
- (-2,0)
- (0,0)
- (0,2)
- (0, 1-3).
- Jibu
-
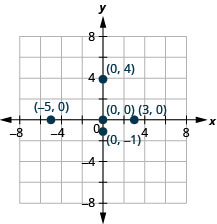
Panda kila hatua:
- (-5,0)
- (3,0)
- (0,0)
- (0, -1)
- (0,4).
- Jibu
-
Katika algebra, kuwa na uwezo wa kutambua kuratibu za hatua iliyoonyeshwa kwenye grafu ni muhimu tu kama kuwa na uwezo wa kupanga njama. Ili kutambua x -kuratibu ya uhakika kwenye grafu, soma namba kwenye x -axis moja kwa moja juu au chini ya uhakika. Ili kutambua y -kuratibu ya uhakika, soma namba kwenye y -axis moja kwa moja upande wa kushoto au kulia wa uhakika. Kumbuka, unapoandika jozi iliyoamriwa tumia utaratibu sahihi, (x, y).
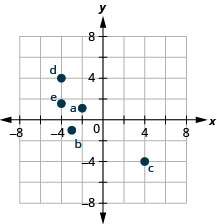
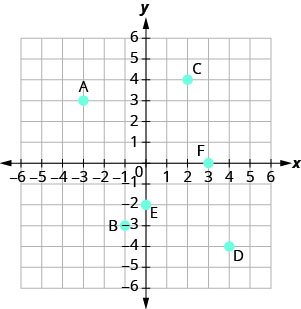
Jina jozi iliyoamriwa ya kila hatua iliyoonyeshwa kwenye mfumo wa kuratibu mstatili.
- Jibu
-
Point A ni juu ya -3 juu ya x -axis, hivyo x -kuratibu ya uhakika ni -3.
Hatua ni upande wa kushoto wa 3 kwenye y -axis, hivyo y -kuratibu ya uhakika ni 3. - Kuratibu za uhakika ni (-3,3).
-
Point B ni chini ya -1 kwenye x -axis, hivyo x -kuratibu ya uhakika ni -1.
Hatua ni upande wa kushoto wa -3 kwenye y -axis, hivyo y -kuratibu ya uhakika ni -3. - Kuratibu za uhakika ni (-1, 1-3).
Point C ni juu ya 2 juu ya x -axis, hivyo x -kuratibu ya uhakika ni 2.
Hatua ni ya haki ya 4 kwenye y -axis, hivyo y -kuratibu ya uhakika ni 4. - Kuratibu ya uhakika ni (2,4).
- Point D ni chini ya 4 juu ya x -axis, hivyo x -kuratibu ya uhakika ni 4.
- Hatua ni kwa haki ya -4 kwenye y -axis, hivyo y -kuratibu ya uhakika ni -4.
- Kuratibu za uhakika ni (4, -4).
-
Point E ni juu ya y -axis katika y=-1 2. Kuratibu za hatua E ni (0, -1).
Point F ni juu ya x -axis katika x=3. Kuratibu ya hatua F ni (3,0).
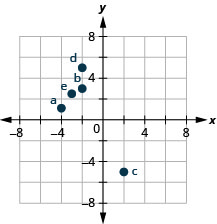
Jina jozi iliyoamriwa ya kila hatua iliyoonyeshwa kwenye mfumo wa kuratibu mstatili.
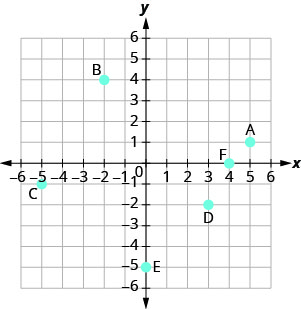
- Jibu
-
A: (5,1) B: (-2,4) C: (-5, -1) D: (3, -2) E: (0, -5) F: (4,0)
Jina jozi iliyoamriwa ya kila hatua iliyoonyeshwa kwenye mfumo wa kuratibu mstatili.
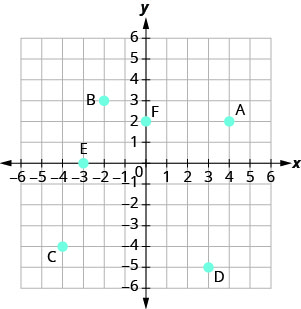
- Jibu
-
A: (4,2) B: (-2,3) C: (-4, -4) D: (3, -5) E: (-3,0) F: (0,2)
Thibitisha Ufumbuzi wa Equation katika Vigezo viwili
Hadi sasa, equations wote una kutatuliwa walikuwa equations na variable moja tu. Katika karibu kila kesi, wakati kutatuliwa equation got hasa ufumbuzi moja. Mchakato wa kutatua equation ulimalizika na taarifa kama x=4. (Kisha, wewe checked ufumbuzi kwa kubadili nyuma katika equation.)
Hapa ni mfano wa equation katika variable moja, na ufumbuzi wake moja.
\[\begin{aligned} 3 x+5 &=17 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
Lakini equations inaweza kuwa na variable zaidi ya moja. Equations na vigezo viwili inaweza kuwa ya fomu Ax+By = C. equations ya fomu hii inaitwa equations linear katika vigezo viwili.
Equation ya fomu Ax+By=C, ambapo A na B si wote sifuri, inaitwa equation linear katika vigezo viwili.
Angalia mstari wa neno katika mstari. Hapa ni mfano wa equation linear katika vigezo mbili, x na y.
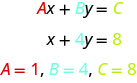
Equation y=-3x+5 pia ni equation linear. Lakini haionekani kuwa katika fomu Ax+By=C Tunaweza kutumia Mali ya Kuongeza ya Usawa na kuiandika tena katika fomu ya Ax+By=C.
\(\begin{array}{llll} {} &{y} &{=} &{-3x + 5} \\ {\text{Add to both sides.}} &{y + 3x } &{=} &{-3x + 5 + 3x} \\{\text{Simplify.}} &{y + 3x} &{=} &{5} \\{\text{Use the Commutative Property to put it in}} &{3x + y} &{=} &{5} \\{Ax+By = C\text{ form.}} &{} &{} &{} \end{array}\)
Kwa kuandika upya y=-3x+5 kama 3x+y = 5, tunaweza kuona kwa urahisi kwamba ni equation linear katika vigezo mbili kwa sababu ni ya fomu Ax+By = C Wakati equation ni katika fomu Ax+By=C, tunasema ni katika hali ya kawaida.
Equation linear ni katika hali ya kawaida wakati imeandikwa Ax+By=C.
Watu wengi wanapendelea kuwa na A, B, na C kuwa integers na\(A\geq 0\) wakati wa kuandika equation linear katika fomu ya kawaida, ingawa si madhubuti muhimu.
Ulinganisho wa mstari una ufumbuzi mkubwa sana. Kwa kila idadi ambayo ni kubadilishwa kwa x kuna sambamba y thamani. Jozi hii ya maadili ni suluhisho la equation linear na inawakilishwa na jozi iliyoamriwa (x, y). Wakati sisi badala ya maadili haya ya x na y katika equation, matokeo yake ni kauli ya kweli, kwa sababu thamani upande wa kushoto ni sawa na thamani upande wa kulia.
Jozi iliyoamriwa (x, y) ni suluhisho la equation ya mstari Ax+By=C, ikiwa equation ni taarifa ya kweli wakati maadili ya x - na y -ya jozi iliyoamriwa yanabadilishwa kwenye equation.
Kuamua ambayo jozi zilizoamriwa ni ufumbuzi wa equation x+4y=8.
(a) (0,2)
(b) (2, -4)
(c) (-4,3)
- Jibu
-
Badilisha x - na y -maadili kutoka kila jozi kuamuru katika equation na kuamua kama matokeo ni taarifa ya kweli.
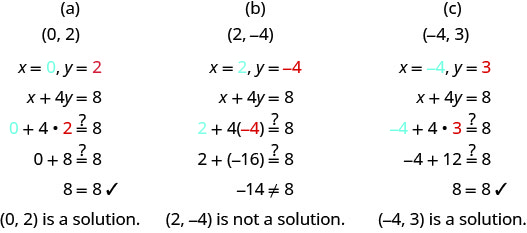
Ni ipi kati ya jozi zifuatazo zilizoamriwa ni ufumbuzi wa 2x+3y=6?
- (3,0)
- (2,0)
- (6,-2)
- Jibu
-
1, 3
Ni ipi kati ya jozi zifuatazo zilizoamriwa ni ufumbuzi wa equation 4x-y=8?
- (0,8)
- (2,0)
- (1, -4)
- Jibu
-
2, 3
Ni ipi kati ya jozi zifuatazo zilizoamriwa ni ufumbuzi wa equation y=5x-1?
(a) (0, -1)
(b) (1,4)
(c) (-2, -7)
- Jibu
-
Badilisha x - na y -maadili kutoka kila jozi kuamuru katika equation na kuamua kama matokeo katika taarifa ya kweli.
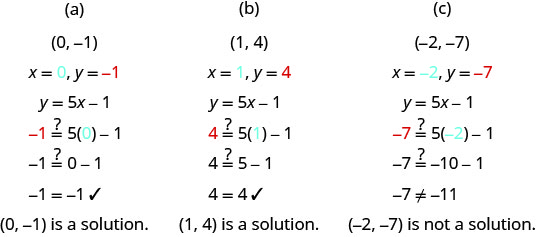
Ni ipi kati ya jozi zifuatazo zilizoamriwa ni ufumbuzi wa equation y=4x-3?
- (0.3)
- (1,1)
- (-1, -1)
- Jibu
-
2
Ni ipi kati ya jozi zifuatazo zilizoamriwa ni ufumbuzi wa equation y=-2x+6?
- (0,6)
- (1,4)
- (-1, -2)
- Jibu
-
1, 2
Jaza Jedwali la Ufumbuzi wa Equation ya Mstari katika Vigezo viwili
Katika mifano hapo juu, tulibadilisha x - na y -maadili ya jozi iliyotolewa kuamuru kuamua kama au la ilikuwa suluhisho la equation linear. Lakini unapataje jozi zilizoamriwa ikiwa hazipewi? Ni rahisi zaidi kuliko unaweza kufikiri - unaweza tu kuchukua thamani kwa xx na kisha kutatua equation kwa yy. Au, chagua thamani kwa yy na kisha usuluhishe kwa xx.
Tutaweza kuanza kwa kuangalia ufumbuzi wa equation y = 5x-1 kwamba sisi kupatikana katika Zoezi\(\PageIndex{13}\). Tunaweza muhtasari habari hii katika meza ya ufumbuzi, kama inavyoonekana katika Jedwali\(\PageIndex{1}\).
| y=5x-1 | ||
| x | y | (x, y) |
| 0 | -1 | (0, -1) |
| 1 | 4 | (1,4) |
Ili kupata ufumbuzi wa tatu, tutaweza basi x = 2 na kutatua kwa y.
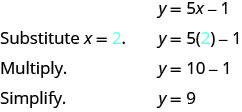
Jozi zilizoamriwa (2,9) ni suluhisho la y=5x-1. Tutaiongeza kwenye Jedwali\(\PageIndex{2}\).
| y=5x-1 | ||
| x | y | (x, y) |
| 0 | -1 | (0, -1) |
| 1 | 4 | (1,4) |
| 2 | 9 | (2,9) |
Tunaweza kupata ufumbuzi zaidi kwa equation kwa kubadilisha katika thamani yoyote ya x au thamani yoyote ya y na kutatua equation kusababisha kupata jozi nyingine kuamuru kwamba ni suluhisho. Kuna ufumbuzi mkubwa wa equation hii.
Jedwali kamili ili kupata ufumbuzi wa tatu kwa equation y = 4x-1 2.
| y=4x-2 | ||
| x | y | (x, y) |
| 0 | ||
| -1 | ||
| 2 | ||
- Jibu
-
Mbadala x=0, x=-1, na x=2 ndani ya y=4x-1.
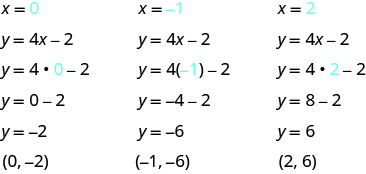
-
Matokeo ni muhtasari katika Jedwali\(\PageIndex{4}\).
y=4x-2 x y (x, y) 0 -2 (0, -2) -1 -6 (-1, -6) 2 6 (2,6) Jedwali\(\PageIndex{4}\)
Jaza meza ili upate ufumbuzi wa tatu kwa usawa huu: y=3x-1.
| y=3x-1 | ||
| x | y | (x, y) |
| 0 | ||
| -1 | ||
| 2 | ||
- Jibu
-
y=3x-1 x y (x, y) 0 -1 (0, -1) -1 -4 (-1, -4) 2 5 (2, 5) Jedwali\(\PageIndex{6}\)
Jaza meza ili kupata ufumbuzi wa tatu kwa equation hii: y=6x+1.
| y=6x+1 | ||
| x | y | (x, y) |
| -2 | ||
- Jibu
-
y=6x+1 x y (x, y) 0 1 (0,1) 1 7 (1,7) -2 -11 (-2, -11) Jedwali\(\PageIndex{8}\)
Jedwali kamili\(\PageIndex{9}\) ili kupata ufumbuzi wa tatu kwa equation 5x-4y=20.
| 5x-4y=20 | ||
| x | y | (x, y) |
| 0 | ||
| 5 | ||
- Jibu
-
Badilisha thamani iliyotolewa katika equation 5x-4y=20 na kutatua kwa variable nyingine. Kisha, jaza maadili katika meza.
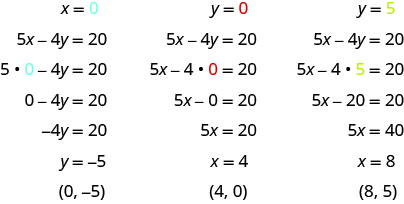
-
Matokeo ni muhtasari katika Jedwali\(\PageIndex{10}\).
5x-4y=20 x y (x, y) 0 -5 (0, -5) 4 0 (4,0) 8 5 (8,5) Jedwali\(\PageIndex{10}\)
Jaza meza ili upate ufumbuzi wa tatu kwa usawa huu: 2x-5y=20.
| 2x-5y=20 | ||
| x | y | (x, y) |
| -5 | ||
- Jibu
-
2x-5y=20 x y (x, y) 0 -4 (0, -4) 10 0 (10,0) -5 -6 (-5, -6) Jedwali\(\PageIndex{12}\)
Jaza meza ili upate ufumbuzi wa tatu kwa usawa huu: 3x-4y=12.
| 3x-4y=12 | ||
| x | y | (x, y) |
| -4 | ||
- Jibu
-
3x-4y=12 x y (x, y) 0 —3 (0, 1-3) 4 0 (4,0) -4 -6 (-4, -6) Jedwali\(\PageIndex{14}\)
Pata ufumbuzi wa Equation ya Mstari
Ili kupata ufumbuzi wa equation linear, kwa kweli unaweza kuchukua idadi yoyote unataka mbadala katika equation kwa x au y Lakini tangu itabidi kutumia idadi hiyo kutatua kwa variable nyingine ni wazo nzuri ya kuchagua idadi hiyo ni rahisi kufanya kazi na.
Wakati equation iko katika y -fomu, na y yenyewe upande mmoja wa equation, kwa kawaida ni rahisi kuchagua maadili ya x na kisha kutatua kwa y.
Pata ufumbuzi wa tatu kwa equation y=-3x+2.
- Jibu
-
Tunaweza kubadilisha thamani yoyote tunayotaka kwa x au thamani yoyote kwa y Tangu equation iko katika y -fomu, itakuwa rahisi kubadilisha katika maadili ya x Hebu tuchukue x=0, x = 1, na x = -1.



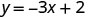
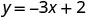
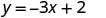
Badala thamani katika equation. 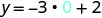
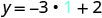
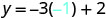
Kurahisisha. 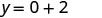
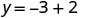
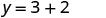
Kurahisisha. 
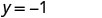

Andika jozi iliyoamriwa. (0, 2) (1, -1) (-1, 5) Angalia. y=-3x+2 y=-3x+2 y=-3x+2 \(2 \stackrel{?}{=} -3 \cdot 0 + 2\) \(-1 \stackrel{?}{=} -3 \cdot 1 + 2\) \(5 \stackrel{?}{=} -3 (-1) + 2\) \(2 \stackrel{?}{=} 0 + 2\) \(-1 \stackrel{?}{=} -3 + 2\) \(5 \stackrel{?}{=} -3 + 2\) \(2 = 2\checkmark\) \(-1 = -1\checkmark\) \(5 = 5\checkmark\) - Jedwali\(\PageIndex{15}\)
-
Hivyo, (0,2), (1, -1) na (-1,5) ni ufumbuzi wote kwa y=-3x+2. Tunawaonyesha katika Jedwali\(\PageIndex{16}\).
y=-3x+2 x y (x, y) 0 2 (0,2) 1 -1 (1, -1) -1 5 (-1,5) Jedwali\(\PageIndex{16}\)
Pata ufumbuzi wa tatu kwa equation hii: y=-2x+3.
- Jibu
-
Majibu yatatofautiana.
Pata ufumbuzi wa tatu kwa equation hii: y=-4x+1.
- Jibu
-
Majibu yatatofautiana.
Tumeona jinsi ya kutumia sifuri kama thamani moja ya x hufanya kutafuta thamani ya y rahisi. Wakati equation iko katika fomu ya kawaida, na x na y upande huo wa equation, kwa kawaida ni rahisi kupata suluhisho moja wakati x=0 kupata suluhisho la pili wakati y=0, na kisha kupata suluhisho la tatu.
Kupata ufumbuzi tatu kwa equation 3x+2y=6.
- Jibu
-
Tunaweza mbadala thamani yoyote tunataka kwa x au thamani yoyote kwa y Tangu equation ni katika hali ya kiwango, hebu pick kwanza x = 0, basi y = 0, na kisha kupata hatua ya tatu.

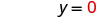

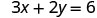
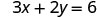
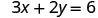
Badala thamani katika equation. 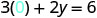
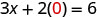
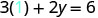
Kurahisisha. 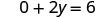
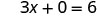
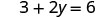
Kutatua. 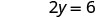
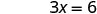
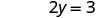
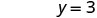

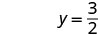
Andika jozi iliyoamriwa. (0, 3) (2, 0) \((1,\frac{3}{2})\) Angalia. 3x+2y=6 3x+2y=6 3x+2y=6 \(3\cdot 0 + 2\cdot 3 \stackrel{?}{=} 6\) \(3\cdot 2 + 2\cdot 0 \stackrel{?}{=} 6\) \(3\cdot 1 + 2\cdot \frac{3}{2} \stackrel{?}{=} 6\) \(0 + 6 \stackrel{?}{=} 6\) \(6 + 0 \stackrel{?}{=} 6\) \(3 + 3 \stackrel{?}{=} 6\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) Jedwali\(\PageIndex{17}\) Hivyo (0,3), (2,0), na wote\((1,\frac{3}{2})\) ni ufumbuzi wa equation 3x+2y=6. Tunaweza kuorodhesha ufumbuzi huu tatu katika Jedwali\(\PageIndex{18}\).
3x+2y=63x+2y=6 x y (x, y) 0 3 (0,3) 2 0 (2,0) 1 \(\frac{3}{2}\) \((1, \frac{3}{2})\) Jedwali\(\PageIndex{18}\)
Pata ufumbuzi wa tatu kwa equation 2x+3y=6.
- Jibu
-
Majibu yatatofautiana.
Kupata ufumbuzi tatu kwa equation 4x+2y=8.
- Jibu
-
Majibu yatatofautiana.
Dhana muhimu
- Ishara Sampuli za Quadrants
\(\begin{array}{ll}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\) - Pointi kwenye Axes
- Kwenye x -axis, y=0. Pointi na y -kuratibu sawa na 0 ni juu ya x -axis, na kuwa na kuratibu (a,0).
- Kwenye y -axis, x=0. Pointi na x -kuratibu sawa na 0 ni juu ya y -axis, na kuwa na kuratibu (0, b).
- Suluhisho la Equation ya Mstari
- Jozi iliyoamriwa (x, y) ni suluhisho la equation ya mstari Ax+By=C, ikiwa equation ni taarifa ya kweli wakati maadili ya x - na y - ya jozi iliyoamriwa yanabadilishwa kwenye equation.
faharasa
- equation linear
- Equation linear ni ya fomu Ax+By = C, ambapo A na B si wote sifuri, inaitwa equation linear katika vigezo mbili.
- jozi iliyoamriwa
- Jozi iliyoamriwa (x, y) inatoa kuratibu ya uhakika katika mfumo wa kuratibu mstatili.
- asili
- Hatua (0,0) (0,0) inaitwa asili. Ni hatua ambapo x -axis na y -axis intersect.
- roboduara
- Mhimili wa x na y -axis hugawanya ndege katika mikoa minne, inayoitwa quadrants.
- mfumo wa kuratibu mstatili
- Mfumo wa gridi hutumika katika algebra kuonyesha uhusiano kati ya vigezo viwili; pia huitwa xy -plane au 'kuratibu plane'.
- x -kuratibu
- Nambari ya kwanza katika jozi iliyoamriwa (x, y).
- y -kuratibu
- Nambari ya pili katika jozi iliyoamriwa (x, y).


