3.1: Tumia Mkakati wa Kutatua Matatizo

Last updated
Save as PDF

Page ID: 177688

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Njia ya matatizo ya neno na mtazamo mzuri
Tumia mkakati wa kutatua matatizo kwa matatizo ya neno
Tatua matatizo ya nambari

Kumbuka

Kabla ya kuanza, fanya jaribio hili la utayari.

Tafsiri “6 chini ya mara mbili x” katika usemi wa algebraic.
Kama amekosa tatizo hili, kupitia Zoezi 1.3.43.
Kutatua:$\frac{2}{3}x=24$.
Ikiwa umekosa tatizo hili, tathmini Zoezi 2.2.10.
Kutatua:$3x+8=14$.
Ikiwa umekosa tatizo hili, tathmini Zoezi 2.3.1.

Njia ya Neno Matatizo na Mtazamo Mzuri

“Kama unafikiri unaweza... au unafikiri huwezi... uko sahihi.” —Henry Ford

Dunia imejaa matatizo ya neno! Je! Mapato yangu yananihitimu kukodisha ghorofa hiyo? Ni ngumi ngapi ninahitaji kufanya kwa ajili ya chama? Nini ukubwa wa almasi ninaweza kumudu kununua mpenzi wangu? Lazima niruke au kuendesha gari kwa muungano wa familia yangu? Ni kiasi gani cha fedha ninahitaji kujaza gari na gesi? Ni ncha gani nipaswa kuondoka kwenye mgahawa? Ni soksi ngapi ninazoziba kwa likizo? Je, ni ukubwa gani wa Uturuki ambao ninahitaji kununua kwa chakula cha jioni cha Shukrani, na kisha ni wakati gani ninahitaji kuiweka kwenye tanuri? Ikiwa mimi na dada yangu tunununua mama yetu zawadi, kila mmoja wetu analipa kiasi gani?

Sasa kwa kuwa tunaweza kutatua equations, tuko tayari kutumia ujuzi wetu mpya kwa matatizo ya neno. Unajua mtu yeyote ambaye amekuwa na uzoefu mbaya katika siku za nyuma na matatizo ya neno? Je, umewahi kuwa na mawazo kama mwanafunzi chini (Kielelezo$\PageIndex{1}$)?

Mwanafunzi anaonyeshwa na Bubbles mawazo akisema “Sijui kama kuongeza, Ondoa, kuzidisha, au kugawa! ,” “Sielewi matatizo ya neno! ,” “Walimu wangu kamwe alielezea hili! ,” “Kama mimi tu ruka matatizo yote neno, Mimi pengine bado kupita darasa,” na “Mimi tu hawezi kufanya hivyo!” — Kielelezo$\PageIndex{1}$: Mawazo mabaya yanaweza kuwa vikwazo vya mafanikio.

Tunapohisi hatuna udhibiti, na kuendelea kurudia mawazo mabaya, tunaanzisha vikwazo vya kufanikiwa. Tunahitaji kutuliza hofu zetu na kubadilisha hisia zetu hasi.

Anza na slate safi na kuanza kufikiri mawazo mazuri. Kama sisi kuchukua udhibiti na kuamini tunaweza kuwa na mafanikio, tutakuwa na uwezo wa bwana matatizo neno! Soma mawazo mazuri katika Kielelezo$\PageIndex{2}$ na kuwaambia kwa sauti kubwa.

Mwanafunzi anaonyeshwa akiwa na Bubbles za mawazo akisema “Wakati matatizo ya neno yalikuwa magumu katika siku za nyuma, nadhani ninaweza kuwajaribu sasa,” “Nimeandaliwa vizuri zaidi sasa. Nadhani nitaanza kuelewa matatizo ya neno,” “Nadhani naweza! Nadhani naweza! ,” na “Inaweza kuchukua muda, lakini naweza kuanza kutatua matatizo ya neno.” — Kielelezo$\PageIndex{2}$: Kufikiri mawazo mazuri ni hatua ya kwanza kuelekea mafanikio.

Fikiria kitu, nje ya shule, ambacho unaweza kufanya sasa lakini hakuweza kufanya miaka 3 iliyopita. Je, ni kuendesha gari? Snowboarding? Kupika chakula cha gourmet? Akizungumza lugha mpya? Uzoefu wako wa zamani na matatizo ya neno ulitokea wakati ulipokuwa mdogo-sasa uko mkubwa na tayari kufanikiwa!

Tumia Mkakati wa Kutatua Matatizo kwa Matatizo ya Neno

Tumepitia kutafsiri misemo ya Kiingereza katika maneno ya algebraic, kwa kutumia msamiati wa msingi wa hisabati na alama. Pia tumetafsiri sentensi za Kiingereza katika milinganyo ya algebraic na kutatuliwa matatizo fulani ya neno. matatizo neno kutumika math kwa hali ya kila siku. Sisi tena hali katika sentensi moja, kupewa variable, na kisha aliandika equation kutatua tatizo. Njia hii inafanya kazi kwa muda mrefu kama hali hiyo inajulikana na hesabu sio ngumu sana.

Sasa, tutaweza kupanua mkakati wetu ili tuweze kuitumia kwa mafanikio kutatua tatizo lolote neno. Tutaweza orodha mkakati hapa, na kisha tutaweza kutumia kutatua baadhi ya matatizo. Sisi muhtasari chini mkakati madhubuti kwa ajili ya kutatua tatizo.

TUMIA MKAKATI WA KUTATUA TATIZO KUTATUA MATATIZO YA NENO.

Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
Tambua kile tunachotafuta.
Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho.
Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Kisha, tafsiri sentensi ya Kiingereza kwenye equation ya algebraic.
Kutatua equation kutumia mbinu nzuri algebra.
Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
Jibu swali kwa sentensi kamili.

Zoezi$\PageIndex{1}$

Pilar alinunua mfuko wa fedha kwa ajili ya kuuza$$18$, ambayo ni nusu ya bei ya awali. Je! Bei ya awali ya mfuko wa fedha ilikuwa nini?

Jibu

Hatua ya 1. Soma tatizo. Soma tatizo mara mbili au zaidi ikiwa ni lazima. Angalia maneno yoyote yasiyojulikana katika kamusi au kwenye mtandao.

Katika tatizo hili, ni wazi nini kinachojadiliwa? Je, kila neno linajulikana?

Hebu p = bei ya awali ya mfuko wa fedha.

Hatua ya 2. Tambua unachotafuta. Je! Umewahi kwenda kwenye chumba chako cha kulala ili kupata kitu na kisha kusahau kile ulichotafuta? Ni vigumu kupata kitu ikiwa hujui ni nini! Soma tatizo tena na uangalie maneno ambayo yanakuambia unachotafuta!

Katika tatizo hili, maneno “ilikuwa bei gani ya awali ya mfuko wa fedha” inatuambia kile tunachohitaji kupata.

Hatua ya 3. Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho. Tunaweza kutumia barua yoyote kwa ajili ya kutofautiana, lakini kuchagua moja kwamba inafanya kuwa rahisi kukumbuka nini inawakilisha.

Hatua ya 4. Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Tafsiri sentensi ya Kiingereza katika equation ya algebraic.

Soma tena tatizo kwa uangalifu ili uone jinsi habari iliyotolewa inahusiana. Mara nyingi, kuna sentensi moja ambayo inatoa habari hii, au inaweza kusaidia kuandika sentensi moja na taarifa zote muhimu. Tafuta maneno ya kidokezo ili kusaidia kutafsiri sentensi katika algebra. Tafsiri sentensi katika equation.

Rejesha tatizo katika sentensi moja na taarifa zote muhimu.	$\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}$
Tafsiri katika equation.	$18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p$

Hatua ya 5. Kutatua equation kutumia mbinu nzuri algebraic. Hata kama unajua suluhisho mara moja, kutumia mbinu nzuri za algebraic hapa zitakuandaa vizuri kutatua matatizo ambayo hayana majibu ya wazi.

Kutatua equation.	$18 = \frac{1}{2}p$
Panua pande zote mbili kwa 2.	$ {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p $
Kurahisisha.	$36 = p$

Hatua ya 6. Angalia jibu katika tatizo ili uhakikishe kuwa ni busara. Sisi kutatuliwa equation na kugundua kwamba$p=36$, ambayo ina maana “bei ya awali” ilikuwa$$36$.

Je, $36 ina maana katika tatizo? Ndiyo, kwa sababu 18 ni nusu moja ya 36, na mfuko huo ulikuwa unauzwa kwa nusu ya bei ya awali.

Ikiwa hii ilikuwa zoezi la kazi za nyumbani, kazi yetu inaweza kuonekana kama hii:

Pilar alinunua mfuko wa fedha kwa ajili ya kuuza$$18$, ambayo ni nusu ya bei ya awali. Je! Bei ya awali ya mfuko wa fedha ilikuwa nini?

Hatua ya 7. Jibu swali kwa sentensi kamili. Tatizo liliuliza “Nini bei ya awali ya mfuko wa fedha?”

Jibu la swali ni: “Bei ya awali ya mfuko wa fedha ilikuwa $36.”

	Hebu bei$p =$ ya awali.
	$18$ni nusu ya bei ya awali.
	$18 = \frac{1}{2}p$
Kuzidisha pande zote mbili na$2$.	$ {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p $
Kurahisisha.	$36 = p$
Angalia. Je$$36$! Ni bei nzuri ya mfuko wa fedha?
Ndiyo.
Ni nusu$18$ moja ya$36$?
$18 \stackrel{?}{=} \frac{1}{2}\cdot 36$
$18 = 18\checkmark$
	Bei ya awali ya mfuko huo ilikuwa$$36$.

Zoezi$\PageIndex{2}$

Joaquin alinunua bookcase kuuzwa kwa$$120$, ambayo ilikuwa theluthi mbili ya bei ya awali. Nini ilikuwa bei ya awali ya bookcase?

Jibu: $$180$

Zoezi$\PageIndex{3}$

Sehemu ya tano ya nyimbo katika orodha ya kucheza ya Mariel ni nchi. Ikiwa kuna nyimbo za$16$ nchi, ni idadi gani ya nyimbo katika orodha ya kucheza?

Jibu: $40$

Hebu jaribu njia hii na mfano mwingine.

Zoezi$\PageIndex{4}$

Ginny na wanafunzi wenzake waliunda kundi la utafiti. Idadi ya wasichana katika kundi la utafiti ilikuwa tatu zaidi ya mara mbili idadi ya wavulana. Kulikuwa na$11$ wasichana katika kundi la utafiti. Wavulana wangapi walikuwa katika kundi la utafiti?

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	Wavulana wangapi walikuwa katika kundi la utafiti?
Hatua ya 3. Jina. Chagua variable kuwakilisha idadi ya wavulana.	Hebu idadi$n=$ ya wavulana.
Hatua ya 4. Tafsiri. Rejesha tatizo katika sentensi moja na taarifa zote muhimu.	$\color{cyan} \underbrace{\color{black}\textbf{The number}\\ \color{black}\textbf{of girls}(11)} \quad \underbrace{\strut \text{ } \\ \color{black}\textbf{was}} \quad \underbrace{\color{black}\textbf{three more than}\\ \color{black}\textbf{twice the number of boys}}$
Tafsiri katika equation.	$\qquad 11 \qquad \quad = \qquad \qquad \quad 2b + 3$
Hatua ya 5. Kutatua equation.	$\quad 11 = 2b + 3 $
Ondoa 3 kutoka kila upande.	$\quad 11 \,{\color{red}{- \,3}} = 2b + 3 \,{\color{red}{- \,3}} $
Kurahisisha.	$\quad 8 = 2b $
Gawanya kila upande kwa 2.	$ \quad \dfrac{8}{\color{red}{2}}=\dfrac{2b}{\color{red}{2}} $
Kurahisisha.	$\quad 4 = b$
Hatua ya 6. Angalia. Kwanza, ni jibu letu linalofaa? Ndiyo, kuwa na$4$ wavulana katika kundi la utafiti inaonekana sawa. Tatizo linasema idadi ya wasichana ilikuwa$3$ zaidi ya mara mbili idadi ya wavulana. Ikiwa kuna wavulana wanne, je, hiyo inafanya wasichana kumi na mmoja? Mara mbili$4$ wavulana ni$8$. Tatu zaidi kuliko$8$ ilivyo$11$.
Hatua ya 7. Jibu swali.	Kulikuwa na$4$ wavulana katika kundi la utafiti.

Zoezi$\PageIndex{5}$

Guillermo alinunua vitabu na daftari katika duka la vitabu. Idadi ya vitabu vya vitabu ilikuwa$3$ zaidi ya mara mbili idadi ya daftari. Alinunua$7$ vitabu vya vitabu. Alinunua daftari ngapi?

Jibu: $2$

Zoezi$\PageIndex{6}$

Gerry kazi Sudoku puzzles na crossword puzzles wiki hii. Idadi ya puzzles ya Sudoku aliyoimaliza ni nane zaidi ya mara mbili idadi ya puzzles ya crossword. Alimaliza puzzles za$22$ Sudoku. Alifanya puzzles ngapi za crossword?

Jibu: $7$

Tatua Matatizo ya Idadi

Sasa kwa kuwa tuna mkakati wa kutatua tatizo, tutatumia kwenye aina mbalimbali za matatizo ya neno. Aina ya kwanza tutakayofanya kazi ni “matatizo ya namba.” Idadi matatizo kutoa baadhi ya dalili kuhusu namba moja au zaidi. Sisi kutumia dalili hizi kuandika equation. Matatizo ya namba hayatokea kila siku, lakini hutoa utangulizi mzuri wa kufanya mkakati wa kutatua tatizo lililoelezwa hapo juu.

Zoezi$\PageIndex{7}$

Tofauti ya idadi na sita ni$13$. Pata nambari.

Jibu

Hatua ya 1. Soma tatizo. Je! Maneno yote yanajulikana?
Hatua ya 2. Tambua kile tunachotafuta.	idadi
Hatua ya 3. Jina. Chagua variable kuwakilisha idadi.	Hebu$n=$ idadi.
Hatua ya 4. Tafsiri. Kumbuka kuangalia maneno ya kidokezo kama “tofauti... ya... na...”
Rejesha tatizo kama sentensi moja.	$\color{cyan} \underbrace{\color{black}\textbf{The difference of the number and }\mathbf{6}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\strut \color{black}\mathbf{13}}$
Tafsiri katika equation.	$\qquad \qquad \qquad n-6 \qquad \qquad \qquad \quad = \quad 13$
Hatua ya 5. Kutatua equation.	$\quad n - 6 = 13$
Kurahisisha.	$\quad n =19$
Hatua ya 6. Angalia.
Tofauti ya$19$ na$6$ ni$13$. Ni hundi!
Hatua ya 7. Jibu swali.	Nambari ni$19$.

Zoezi$\PageIndex{8}$

Tofauti ya idadi na nane ni$17$. Pata nambari.

Jibu: $25$

Zoezi$\PageIndex{9}$

Tofauti ya idadi na kumi na moja ni$−7$. Pata nambari.

Jibu: $4$

Zoezi$\PageIndex{10}$

Jumla ya mara mbili namba na saba ni$15$. Pata nambari.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	idadi
Hatua ya 3. Jina. Chagua variable kuwakilisha idadi.	Hebu$n =$ idadi.
Hatua ya 4. Tafsiri.
Rejesha tatizo kama sentensi moja.	$.$
Tafsiri katika equation.	$.$
Hatua ya 5. Kutatua equation.	$.$
Ondoa 7 kutoka kila upande na kurahisisha.	$.$
Gawanya kila upande kwa 2 na kurahisisha.	$.$
Hatua ya 6. Angalia.
Je, jumla ya mara mbili 4 na 7 ni sawa na 15?
$\begin{array} {rrl} {2\cdot 4 + 7} &{\stackrel{?}{=}}& {15} \\ {15} &{=} &{15\checkmark} \end{array}$
Hatua ya 7. Jibu swali.	Nambari ni$4$.

Je, taarifa kwamba sisi kushoto nje baadhi ya hatua kama sisi kutatuliwa equation hii? Ikiwa bado haujawa tayari kuondoka hatua hizi, andika kama unavyohitaji.

Zoezi$\PageIndex{11}$

Jumla ya mara nne namba na mbili ni$14$. Pata nambari.

Jibu: $3$

Zoezi$\PageIndex{12}$

Jumla ya mara tatu idadi na saba ni$25$. Pata nambari.

Jibu: $6$

Baadhi ya matatizo ya neno namba hutuuliza kupata namba mbili au zaidi. Inaweza kuwa kumjaribu kuwaita wote kwa vigezo tofauti, lakini hadi sasa tuna tu kutatuliwa equations na variable moja. Ili kuepuka kutumia variable zaidi ya moja, tutafafanua idadi katika suala la kutofautiana sawa. Hakikisha kusoma tatizo kwa makini ili kugundua jinsi namba zote zinahusiana.

Zoezi$\PageIndex{13}$

Nambari moja ni tano zaidi ya nyingine. Jumla ya namba ni 21. Kupata idadi.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.		Tunatafuta namba mbili.
Hatua ya 3. Jina. Tuna namba mbili kwa jina na haja ya jina kwa kila.
Chagua variable kuwakilisha namba ya kwanza.		Hebu$n=1^{st}$ idadi.
Tunajua nini kuhusu namba ya pili?		Nambari moja ni tano zaidi ya nyingine.
		$n+5=2^{nd}$namba
Hatua ya 4. Tafsiri. Rejesha tatizo kama sentensi moja na taarifa zote muhimu.		Jumla ya namba ya 1 ^na nambari ya 2 ^nd ni 21.
Tafsiri katika equation.		$.$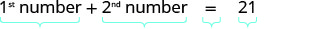
Badilisha maneno ya kutofautiana.		$.$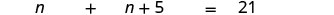
Hatua ya 5. Kutatua equation.		$.$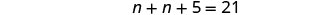
Kuchanganya kama maneno.		$.$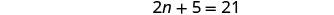
Ondoa 5 kutoka pande zote mbili na kurahisisha.		$.$
Gawanya na 2 na kurahisisha.		$.$
Pata namba ya pili, pia.		$.$
		$.$
		$.$
Hatua ya 6. Angalia.
Je! Nambari hizi zinaangalia tatizo?
Je, namba moja$5$ zaidi kuliko nyingine?	$13\stackrel{?}{=} 8 + 5$
Ni kumi na tatu$5$ zaidi ya$8$? Ndiyo.	$13 = 13\checkmark$
Je, ni jumla ya namba mbili$21$?	$8 + 13 \stackrel{?}{=} 21$
	$21 = 21\checkmark$
Hatua ya 7. Jibu swali.		Idadi ni$8$ na$13$.

Zoezi$\PageIndex{14}$

Nambari moja ni sita zaidi kuliko nyingine. Jumla ya namba ni ishirini na nne. Kupata idadi.

Jibu: 9, 15

Zoezi$\PageIndex{15}$

Jumla ya namba mbili ni hamsini na nane. Nambari moja ni nne zaidi ya nyingine. Kupata idadi.

Jibu: 27, 31

Zoezi$\PageIndex{16}$

Jumla ya namba mbili ni hasi kumi na nne. Nambari moja ni nne chini ya nyingine. Kupata idadi.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.		Tunatafuta namba mbili.
Hatua ya 3. Jina.
Chagua variable.		Hebu$n=1^{st}$ idadi.
Nambari moja ni 4 chini ya nyingine.		$n−4=2^{nd}$namba
Hatua ya 4. Tafsiri.
Andika kama sentensi moja.		Jumla ya namba 2 ni hasi 14.
Tafsiri katika equation.		$.$
Hatua ya 5. Kutatua equation.		$.$
Kuchanganya kama maneno.		$.$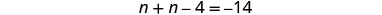
Kuongeza 4 kwa kila upande na kurahisisha.		$.$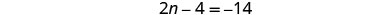
Kurahisisha.		$.$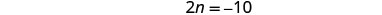
		$.$
		$.$
		$.$
		$.$
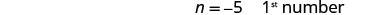
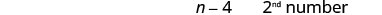
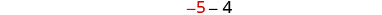
Hatua ya 6. Angalia.
Je, ni -9 nne chini ya -5?	$-5-4\stackrel{?}{=}-9$
	$-9 = -9 \checkmark$
Je, jumla yao ni 14-14?	$-5+ (-9)\stackrel{?}{=}-14$
	$-14 = -14 \checkmark$
Hatua ya 7. Jibu swali.		Namba ni -5 na -9.

Zoezi$\PageIndex{17}$

Jumla ya namba mbili ni hasi ishirini na tatu. Nambari moja ni saba chini ya nyingine. Kupata idadi.

Jibu: -15, -8

Zoezi$\PageIndex{18}$

Jumla ya namba mbili ni$−18$. Nambari moja ni$40$ zaidi ya nyingine. Kupata idadi.

Jibu: -29, 11

Zoezi$\PageIndex{19}$

Nambari moja ni kumi zaidi ya mara mbili nyingine. Jumla yao ni moja. Kupata idadi.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua unachotafuta.		Tunatafuta namba mbili.
Hatua ya 3. Jina.
Chagua variable.		Hebu$x=1^{st}$ idadi.
Nambari moja ni 10 zaidi ya mara mbili nyingine.		$2x+10=2^{nd}$namba
Hatua ya 4. Tafsiri.
Rejesha tena kama sentensi moja.		Jumla yao ni moja.
		Jumla ya namba mbili ni 1.
Tafsiri katika equation.		$.$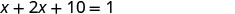
Hatua ya 5. Kutatua equation.
Kuchanganya kama maneno.		$.$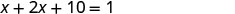
Ondoa 10 kutoka kila upande.		$.$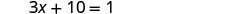
Gawanya kila upande kwa 3.		$.$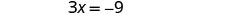
		$.$
		$.$
		$.$
		$.$
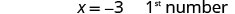
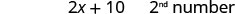
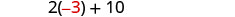
Hatua ya 6. Angalia.
Je, kumi zaidi ya mara mbili -3 ni sawa na 4?	$2(-3) + 10 \stackrel{?}{=} 4$
	$-6 + 10 \stacktel{?}{=} 4$
	$4 = 4\checkmark$
Je, jumla yao ni 1?	$-3 + 4 \stackrel{?}{=} 1$
	$1 = 1\checkmark$
Hatua ya 7. Jibu swali.		Namba ni -3 na -4.

Zoezi$\PageIndex{20}$

Nambari moja ni nane zaidi ya mara mbili nyingine. Jumla yao ni hasi nne. Kupata idadi.

Jibu: $-4,\; 0$

Zoezi$\PageIndex{21}$

Nambari moja ni tatu zaidi ya mara tatu nyingine. Jumla yao ni$−5$. Kupata idadi.

Jibu: $-3,\; -2$

Baadhi ya matatizo ya idadi huhusisha integers mfululizo. Integers mfululizo ni integers kwamba mara moja kufuata kila mmoja. Mifano ya integers mfululizo ni:

\[\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}\]

Angalia kwamba kila namba ni moja zaidi ya namba iliyotangulia. Hivyo kama sisi kufafanua integer kwanza kama$n$, ijayo mfululizo integer ni$n+1$. Moja baada ya hayo ni moja zaidi ya$n+1$, hivyo ni$n+1+1$, ambayo ni$n+2$.
\[\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

Zoezi$\PageIndex{22}$

Jumla ya integers mbili mfululizo ni$47$. Kupata idadi.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua unachotafuta.	integers mbili mfululizo
Hatua ya 3. Jina la kila nambari.	Hebu$n=1^{st}$ integer.
	$n+1=$ijayo mfululizo integer
Hatua ya 4. Tafsiri.
Rejesha tena kama sentensi moja.	Jumla ya integers ni$47$.
Tafsiri katika equation.	$.$
Hatua ya 5. Kutatua equation.	$.$
Kuchanganya kama maneno.	$.$
Ondoa 1 kutoka kila upande.	$.$
Gawanya kila upande kwa 2.	$.$
	$.$
	$.$
	$.$
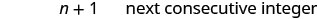
Hatua ya 6. Angalia.
$\begin{array} {lll} {23 + 24} &{\stackrel{?}{=}} &{47} \\ {47} &{=} &{47\checkmark} \end{array}$
Hatua ya 7. Jibu swali.	Integers mbili mfululizo ni 23 na 24.

Zoezi$\PageIndex{23}$

Jumla ya integers mbili mfululizo ni 95. Kupata idadi.

Jibu: 47, 48

Zoezi$\PageIndex{24}$

Jumla ya integers mbili za mfululizo ni -31. Kupata idadi.

Jibu: -16, -15

Zoezi$\PageIndex{25}$

Pata integers tatu za mfululizo ambazo jumla yake ni -42.

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	integers tatu mfululizo
Hatua ya 3. Jina kila moja ya namba tatu.	Hebu$n=1^{st}$ integer.
	$n+1= 2^{nd}$integer mfululizo
	$n+2= 3^{rd}$integer mfululizo
Hatua ya 4. Tafsiri.
Rejesha tena kama sentensi moja.	Jumla ya integers tatu ni$−42$.
Tafsiri katika equation.	$.$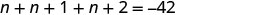
Hatua ya 5. Kutatua equation.	$.$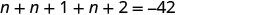
Kuchanganya kama maneno.	$.$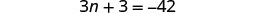
Ondoa 3 kutoka kila upande.	$.$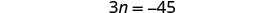
Gawanya kila upande kwa 3.	$.$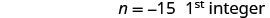
	$.$
	$.$
	$.$
	$.$
	$.$
	$.$
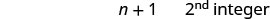
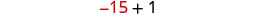
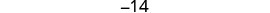
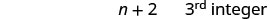
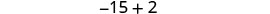
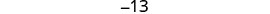
Hatua ya 6. Angalia.
$\begin{array}{lll} {-13 + (-14) + (-15)} &{\stackrel{?}{=}} &{-42} \\ {-42} &{=} &{-42\checkmark} \end{array}$
Hatua ya 7. Jibu swali.	Nambari tatu za mfululizo ni -13, -14, na -15.

Zoezi$\PageIndex{26}$

Pata integers tatu za mfululizo ambazo jumla yake ni -96.

Jibu: -33, -32, -31

Zoezi$\PageIndex{27}$

Pata integers tatu za mfululizo ambazo jumla yake ni -36.

Jibu: -13, -12, -11

Sasa kwa kuwa tumefanya kazi na integers mfululizo, sisi kupanua kazi yetu ni pamoja na mfululizo hata integers na integers mfululizo isiyo ya kawaida. Mfululizo hata integers ni hata integers ambazo hufuata mara moja. Mifano ya mfululizo hata integers ni:

\[\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}\]

Angalia kila integer ni$2$ zaidi ya idadi iliyotangulia. Ikiwa tunaita simu ya kwanza$n$, basi ijayo ni$n+2$. Ijayo itakuwa$n+2+2$ au$n+4$.
\[\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

Integers isiyo ya kawaida ya mfululizo ni integers isiyo ya kawaida ambayo hufuata mara moja. Fikiria integers mfululizo isiyo ya kawaida$77$$79$,, na$81$.

\[\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}\]

\[\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

Je, inaonekana ajabu kuongeza 2 (idadi hata) kupata kutoka integer moja isiyo ya kawaida hadi ijayo? Je, kupata idadi isiyo ya kawaida au hata idadi wakati sisi kuongeza 2 kwa 3? kwa 11? kwa 47?

Kama tatizo anauliza kwa idadi mfululizo hata au idadi isiyo ya kawaida, huna kufanya kitu chochote tofauti. Mfano bado ni sawa-kupata kutoka moja isiyo ya kawaida au moja hata integer hadi ijayo, kuongeza 2.

Zoezi$\PageIndex{28}$

Kupata tatu mfululizo hata integers ambao jumla ni 84.

Jibu: \[\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}\]

Zoezi$\PageIndex{29}$

Kupata tatu mfululizo hata integers ambao jumla ni 102.

Jibu: 32, 34, 36

Zoezi$\PageIndex{30}$

Pata integers tatu za mfululizo ambazo jumla yake ni -24.

Jibu: -10, -8, -6

Zoezi$\PageIndex{31}$

Wanandoa wa ndoa pamoja hupata $110,000 kwa mwaka. Mke hupata $16,000 chini ya mara mbili yale mumewe anayopata. Mume anapata nini?

Jibu

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	Mume hupata kiasi gani?
Hatua ya 3. Jina.
Chagua variable kuwakilisha kiasi mume anachopata.	Hebu kiasi$h=$ ambacho mume anachopata.
Mke hupata$$16,000$ chini ya mara mbili.	$2h−16,000$kiasi mke anachopata.
Hatua ya 4. Tafsiri.	Pamoja mume na mke hupata$$110,000$.
Rejesha tatizo katika sentensi moja na taarifa zote muhimu.	$.$
Tafsiri katika equation.	$.$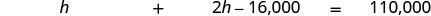
Hatua ya 5. Kutatua equation.	$h + 2h − 16,000 = 110,000$
Kuchanganya kama maneno.	$3h − 16,000 = 110,000$
$16,000$Ongeza pande zote mbili na kurahisisha.	$3h = 126,000$
Gawanya kila upande$3$.	$h = 42,000$
	$$42,000$kiasi mume anapata
	$2h − 16,000$kiasi mke anapata
	$2(42,000) − 16,000$
	$84,000 − 16,000$
	$68,000$
Hatua ya 6. Angalia.
Kama mke anapata$$68,000$ na mume anapata$$42,000$ ni jumla$$110,000$ (? Ndiyo!
Hatua ya 7. Jibu swali.	Mume$$42,000$ hupata mwaka.

Zoezi$\PageIndex{32}$

Kwa mujibu wa Chama cha Taifa cha Wafanyabiashara wa Automobile, wastani wa gharama za gari mwaka 2014 ilikuwa $28,500. Hii ilikuwa $1,500 chini ya 6 mara gharama katika 1975. Gharama ya wastani ya gari ilikuwa nini mwaka 1975?

Jibu: $5000

Zoezi$\PageIndex{33}$

Takwimu za Sensa za Marekani zinaonyesha kuwa bei ya wastani ya nyumba mpya nchini Marekani mnamo Novemba 2014 ilikuwa $280,900. Hii ilikuwa $10,700 zaidi ya mara 14 bei mnamo Novemba 1964. Nini ilikuwa bei ya wastani ya nyumba mpya katika Novemba 1964?

Jibu: $19300

Dhana muhimu

Mkakati wa Kutatua matatizo
1. Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
2. Tambua kile tunachotafuta.
3. Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho.
4. Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Kisha, tafsiri sentensi ya Kiingereza kwenye equation ya algebra.
5. Kutatua equation kutumia mbinu nzuri algebra.
6. Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
7. Jibu swali kwa sentensi kamili.
Integers
mfululizo integers mfululizo ni integers kwamba mara moja kufuata kila mmoja.
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

Mfululizo hata integers ni hata integers ambazo hufuata mara moja.
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

Integers isiyo ya kawaida ya mfululizo ni integers isiyo ya kawaida ambayo hufuata mara moja.
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

	Hebu bei\(p =\) ya awali.
	\(18\)ni nusu ya bei ya awali.
	\(18 = \frac{1}{2}p\)
Kuzidisha pande zote mbili na\(2\).	\( {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p \)
Kurahisisha.	\(36 = p\)
Angalia. Je\($36\)! Ni bei nzuri ya mfuko wa fedha?
Ndiyo.
Ni nusu\(18\) moja ya\(36\)?
\(18 \stackrel{?}{=} \frac{1}{2}\cdot 36\)
\(18 = 18\checkmark\)
	Bei ya awali ya mfuko huo ilikuwa\($36\).

Hatua ya 1. Soma tatizo.
Hatua ya 2. Tambua kile tunachotafuta.	Mume hupata kiasi gani?
Hatua ya 3. Jina.
Chagua variable kuwakilisha kiasi mume anachopata.	Hebu kiasi\(h=\) ambacho mume anachopata.
Mke hupata\($16,000\) chini ya mara mbili.	\(2h−16,000\)kiasi mke anachopata.
Hatua ya 4. Tafsiri.	Pamoja mume na mke hupata\($110,000\).
Rejesha tatizo katika sentensi moja na taarifa zote muhimu.	$.$
Tafsiri katika equation.	$.$
Hatua ya 5. Kutatua equation.	\(h + 2h − 16,000 = 110,000\)
Kuchanganya kama maneno.	\(3h − 16,000 = 110,000\)
\(16,000\)Ongeza pande zote mbili na kurahisisha.	\(3h = 126,000\)
Gawanya kila upande\(3\).	\(h = 42,000\)
	\($42,000\)kiasi mume anapata
	\(2h − 16,000\)kiasi mke anapata
	\(2(42,000) − 16,000\)
	\(84,000 − 16,000\)
	\(68,000\)
Hatua ya 6. Angalia.
Kama mke anapata\($68,000\) na mume anapata\($42,000\) ni jumla\($110,000\) (? Ndiyo!
Hatua ya 7. Jibu swali.	Mume\($42,000\) hupata mwaka.

TUMIA MKAKATI WA KUTATUA TATIZO KUTATUA MATATIZO YA NENO.

Zoezi\(\PageIndex{1}\)

Zoezi\(\PageIndex{2}\)

Zoezi\(\PageIndex{3}\)

Zoezi\(\PageIndex{4}\)

Zoezi\(\PageIndex{5}\)

Zoezi\(\PageIndex{6}\)

Zoezi\(\PageIndex{7}\)

Zoezi\(\PageIndex{8}\)

Zoezi\(\PageIndex{9}\)

Zoezi\(\PageIndex{10}\)

Zoezi\(\PageIndex{11}\)

Zoezi\(\PageIndex{12}\)

Zoezi\(\PageIndex{13}\)

Zoezi\(\PageIndex{14}\)

Zoezi\(\PageIndex{15}\)

Zoezi\(\PageIndex{16}\)

Zoezi\(\PageIndex{17}\)

Zoezi\(\PageIndex{18}\)

Zoezi\(\PageIndex{19}\)

Zoezi\(\PageIndex{20}\)

Zoezi\(\PageIndex{21}\)

Zoezi\(\PageIndex{22}\)

Zoezi\(\PageIndex{23}\)

Zoezi\(\PageIndex{24}\)

Zoezi\(\PageIndex{25}\)

Zoezi\(\PageIndex{26}\)

Zoezi\(\PageIndex{27}\)

Zoezi\(\PageIndex{28}\)

Zoezi\(\PageIndex{29}\)

Zoezi\(\PageIndex{30}\)

Zoezi\(\PageIndex{31}\)

Zoezi\(\PageIndex{32}\)

Zoezi\(\PageIndex{33}\)

Rejesha tatizo katika sentensi moja na taarifa zote muhimu.	\(\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}\)
Tafsiri katika equation.	\(18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p\)