Skip to main content
Global

1.9: Hesabu halisi

  1. Last updated
  2. Save as PDF
  • Page ID
    177998

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Punguza maneno na mizizi ya mraba
    • Tambua integers, namba za busara, namba zisizo na maana, na namba halisi
    • Pata sehemu ndogo kwenye mstari wa nambari
    • Pata decimals kwenye mstari wa nambari
    Kumbuka

    Utangulizi wa kina zaidi wa mada kufunikwa katika sehemu hii inaweza kupatikana katika sura Prealgebra, Decimals na Mali ya Hesabu Real.

    Rahisisha maneno na Mizizi ya Mraba

    Kumbuka kwamba wakati idadi\(n\) imeongezeka kwa yenyewe, tunaandika\(n^{2}\) na kuisoma “\(n\)mraba.” Matokeo huitwa mraba wa\(n\). Kwa mfano,

    \[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

    Vilevile, 121 ni mraba wa 11, kwa sababu\(11^{2}\) ni 121.

    MRABA WA IDADI

    Ikiwa\(n^{2}=m\), basi\(m\) ni mraba wa\(n\).

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Hesabu za mraba” zitakusaidia kuendeleza uelewa bora wa namba kamili za mraba.

    Jaza meza ifuatayo ili kuonyesha mraba wa namba za kuhesabu 1 hadi 15.

    Kuna meza yenye safu mbili na nguzo 17. Mstari wa kwanza unasoma kutoka kushoto kwenda kulia Idadi, n, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, na 15. Mstari wa pili unasoma kutoka kushoto kwenda kulia Mraba, n mraba, tupu, tupu, tupu, tupu, tupu, tupu, tupu, tupu, 64, tupu, tupu, tupu, tupu, na tupu.
    Kielelezo\(\PageIndex{1}\)

    Nambari katika mstari wa pili huitwa namba za mraba kamilifu. Itakuwa na manufaa kujifunza kutambua namba kamili za mraba.

    Mraba ya namba za kuhesabu ni namba nzuri. Nini kuhusu mraba wa idadi hasi? Tunajua kwamba wakati ishara za namba mbili ni sawa, bidhaa zao ni chanya. Hivyo mraba wa idadi yoyote hasi pia ni chanya.

    \[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

    Je! Umeona kwamba mraba huu ni sawa na mraba wa namba nzuri?

    Wakati mwingine tutahitaji kuangalia uhusiano kati ya namba na mraba wao kwa reverse. Kwa sababu\(10^{2}=100\), tunasema 100 ni mraba wa 10. Tunasema pia kwamba 10 ni mizizi ya mraba ya 100. Nambari ambayo mraba ni mm inaitwa mizizi ya mraba ya\(m\).

    MIZIZI YA MRABA YA IDADI

    Ikiwa\(n^{2}=m\), basi\(n\) ni mizizi ya mraba ya\(m\).

    Taarifa\((−10)^{2}=100\) pia, hivyo pia\(−10\) ni mizizi ya mraba ya\(100\). Kwa hiyo, wote wawili\(10\) na\(−10\) ni mizizi ya mraba ya\(100\).

    Kwa hiyo, kila idadi nzuri ina mizizi miwili ya mraba-moja chanya na moja hasi. Nini kama sisi tu alitaka chanya mraba mizizi ya idadi chanya? Ishara kubwa\(\sqrt{m}\), inaashiria mizizi nzuri ya mraba. Mizizi nzuri ya mraba inaitwa mizizi kuu ya mraba. Tunapotumia ishara kali ambayo daima inamaanisha tunataka mizizi kuu ya mraba.

    Tunatumia pia ishara kubwa kwa mizizi ya mraba ya sifuri. Kwa sababu\(0^{2}=0, \sqrt{0}=0\). Angalia kwamba sifuri ina mizizi moja tu ya mraba.

    MRABA MIZIZI NOTATION

    \(\sqrt{m}\)inasoma “mizizi ya mraba ya\(m\)”

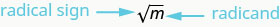
    Mizizi ya mraba hutolewa, na mshale kwa ishara kali (inaonekana kama alama ya alama na mstari usio na usawa unaoenea kutoka mwisho wake mrefu) ulionyesha ishara kali na mshale kwa idadi chini ya ishara kali, ambayo imewekwa alama radicand.

    Ikiwa\(m = n^{2}\), basi\(\sqrt{m} = n\), kwa\(n\geq 0\).

    Mizizi ya mraba ya\(m\)\(\sqrt{m}\),, ni idadi nzuri ambayo mraba ni\(m\).

    Tangu 10 ni mizizi kuu ya mraba ya 100, tunaandika\(\sqrt{100}=10\). Unaweza kutaka kukamilisha meza ifuatayo ili kukusaidia kutambua mizizi ya mraba.

    Kuna meza yenye safu mbili na nguzo 15. mstari wa kwanza anayesoma kutoka kushoto kwenda kulia mizizi ya mraba ya 1, mizizi ya mraba ya 4, mizizi ya mraba ya 9, mizizi ya mraba ya 16, mizizi ya mraba ya 25, mizizi ya mraba ya 36, mizizi ya mraba ya 49, mizizi ya mraba ya 64, mizizi ya mraba ya 81, mizizi ya mraba ya 100, mizizi ya mraba ya 121, mraba mizizi ya 144, mraba mizizi ya 169, na mizizi ya mraba ya 225. Mstari wa pili una safu zote isipokuwa kwa kiini cha kumi chini ya mizizi ya mraba ya 100, ambayo inasoma 10.
    Kielelezo\(\PageIndex{2}\)
    Zoezi\(\PageIndex{1}\)

    Kurahisisha:

    1. \(\sqrt{25}\)
    2. \(\sqrt{121}\)
    Jibu
    1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
    2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
    Zoezi\(\PageIndex{2}\)

    Kurahisisha:

    1. \(\sqrt{36}\)
    2. \(\sqrt{169}\)
    Jibu
    1. 6
    2. 13
    Zoezi\(\PageIndex{3}\)

    Kurahisisha:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Jibu
    1. 4
    2. 14

    Tunajua kwamba kila nambari nzuri ina mizizi miwili ya mraba na ishara kubwa inaonyesha moja nzuri. Tunaandika\(\sqrt{100)=10\). Ikiwa tunataka kupata mizizi ya mraba hasi ya nambari, tunaweka hasi mbele ya ishara kubwa. Kwa mfano,\(-\sqrt{100)=-10\). Tunasoma\(-\sqrt{100)\) kama “kinyume cha mizizi ya mraba ya 10.”

    Zoezi\(\PageIndex{4}\)

    Kurahisisha:

    1. \(-\sqrt{9}\)
    2. \(-\sqrt{144}\)
    Jibu
    1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
    2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
    Zoezi\(\PageIndex{5}\)

    Kurahisisha:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Jibu
    1. -2
    2. -15
    Zoezi\(\PageIndex{6}\)

    Kurahisisha:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Jibu
    1. —9
    2. -10

    Tambua Integers, Nambari za busara, Hesabu zisizofaa, na Hesabu halisi

    Sisi tayari ilivyoelezwa idadi kama kuhesabu s idadi, idadi nzima s, na integers. Ni tofauti gani kati ya aina hizi za namba?

    \[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

    Ni aina gani ya idadi bila sisi kupata kama sisi ilianza na integers wote na kisha ni pamoja na sehemu zote? Nambari ambazo tungependa kuunda seti ya namba za busara. Nambari ya busara ni namba ambayo inaweza kuandikwa kama uwiano wa integers mbili.

    IDADI YA BUSARA

    Nambari ya busara ni idadi ya fomu\(\dfrac{p}{q}\), ambapo p na q ni integers na\(q \neq 0\)

    Nambari ya busara inaweza kuandikwa kama uwiano wa integers mbili.

    Sehemu zote zilizosainiwa, kama vile\(\dfrac{4}{5}\),\(-\dfrac{7}{8}\)\(\dfrac{13}{4}\),\(-\dfrac{20}{3}\) ni namba za busara. Kila nambari na kila denominator ni integer.

    Ni namba integers busara? Kuamua kama integer ni namba ya busara, tunajaribu kuandika kama uwiano wa integers mbili. Kila integer inaweza kuandikwa kama uwiano wa integers kwa njia nyingi. Kwa mfano, 3 ni sawa na\(\dfrac{3}{1}\),\(-\dfrac{6}{2}\),\(\dfrac{9}{3}\),\(\dfrac{12}{4}\),\(-\dfrac{15}{5} \ldots\)

    Njia rahisi ya kuandika integer kama uwiano wa integers ni kuandika kama sehemu na denominator moja.

    \[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

    Kwa kuwa integer yoyote inaweza kuandikwa kama uwiano wa integers mbili, integers zote ni namba za busara! Kumbuka kwamba idadi ya kuhesabu na namba nzima pia ni integers, na hivyo wao, pia, ni busara.

    Nini kuhusu decimals? Je, wao ni busara? Hebu tuangalie wachache kuona kama tunaweza kuandika kila mmoja wao kama uwiano wa integers mbili.

    Tumeona kwamba integers ni namba za busara. Integer\(−8\) inaweza kuandikwa kama decimal\(−8.0\). Kwa hiyo, kwa wazi, baadhi ya decimals ni busara.

    Fikiria juu ya decimal\(7.3\). Je, tunaweza kuandika kama uwiano wa integers mbili? Kwa sababu\(7.3\) ina maana\(7\dfrac{3}{10}\), tunaweza kuandika kama sehemu isiyofaa,\(\dfrac{73}{10}\). Hivyo\(7.3\) ni uwiano wa integers\(73\) na\(10\). Ni idadi ya busara.

    Kwa ujumla, decimal yoyote inayoisha baada ya tarakimu kadhaa (kama vile\(7.3\) au\(−1.2684\)) ni namba ya busara. Tunaweza kutumia thamani ya mahali ya tarakimu ya mwisho kama denominator wakati wa kuandika decimal kama sehemu.

    Zoezi\(\PageIndex{7}\)

    Andika kama uwiano wa integers mbili:

    1. -27
    2. 7.31
    Jibu
    1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
    2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

    Kwa hiyo tunaona kwamba -27 na 7.31 ni namba za busara, kwani zinaweza kuandikwa kama uwiano wa integers mbili.

    Zoezi\(\PageIndex{8}\)

    Andika kama uwiano wa integers mbili:

    1. -24
    2. 3.57
    Jibu
    1. \(\dfrac{-24}{1}\)
    2. \(\dfrac{357}{100}\)
    Zoezi\(\PageIndex{9}\)

    Andika kama uwiano wa integers mbili:

    1. 19-19
    2. 8.41
    Jibu
    1. \(\dfrac{-19}{1}\)
    2. \(\dfrac{841}{100}\)
    Hebu tuangalie fomu ya decimal ya namba tunayojua ni ya busara.

    Tumeona kwamba kila integer ni idadi ya busara, tangu\(a = \dfrac{a}{1}\) kwa integer yoyote,\(a\). Tunaweza pia kubadilisha integer yoyote kwa decimal kwa kuongeza uhakika decimal na sifuri.

    \[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

    Tumeona pia kwamba kila sehemu ni idadi ya busara. Angalia fomu ya decimal ya vipande ambavyo tumezingatia hapo juu.

    \[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

    Mifano hii inatuambia nini?

    Kila nambari ya busara inaweza kuandikwa wote kama uwiano wa integers\(\dfrac{p}{q}\), (, ambapo p na q ni integers na\(q\neq 0\)), na kama decimal kwamba ama ataacha au kurudia.

    Hapa ni namba ambazo tumeangalia hapo juu zilionyesha kama uwiano wa integers na kama decimal:

    FRACTIONS Nambari kamili
    Idadi \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) -2 -1 0 1 2 3
    Uwiano wa Integers \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) \(-\frac{2}{1}\) \(-\frac{1}{1}\) \(\frac{0}{1}\) \(\frac{1}{1}\) \(\frac{2}{1}\) \(\frac{3}{1}\)
    Fomu ya decimal 0.8 -0.875 3.25 \(−6.\overline{6}\) -2.0 -1.0 0.0 1.0 2.0 3.0
    Jedwali\(\PageIndex{1}\)
    IDADI YA BUSARA

    Nambari ya busara ni idadi ya fomu\(\frac{p}{q}\), ambapo p na q ni integers na\(q\neq 0\)

    Fomu yake ya decimal inacha au kurudia.

    Je, kuna decimals yoyote ambayo haina kuacha au kurudia? Ndiyo!

    Nambari\(\pi\) (barua ya Kigiriki pi, inayojulikana “pie”), ambayo ni muhimu sana katika kuelezea miduara, ina fomu ya decimal ambayo haina kuacha au kurudia.

    \[\pi =3.141592654\ldots\]

    Tunaweza hata kuunda muundo wa decimal ambao hauacha au kurudia, kama vile

    \[2.01001000100001\ldots\]

    Hesabu ambazo fomu ya decimal haina kuacha au kurudia haiwezi kuandikwa kama sehemu ya integers. Tunaita namba hizi irrational.

    NAMBARI ISIYO NA MAANA

    Nambari isiyo na maana ni namba ambayo haiwezi kuandikwa kama uwiano wa integers mbili.

    Fomu yake ya decimal haina kuacha na haina kurudia.

    Hebu tufupishe njia tunayoweza kutumia ili kuamua kama namba ni ya busara au isiyo ya maana.

    BUSARA AU IRRATIONAL?

    Ikiwa fomu ya decimal ya nambari

    • kurudia au ataacha, idadi ni ya busara.
    • haina kurudia na haina kuacha, idadi ni irrational.
    Zoezi\(\PageIndex{10}\)

    Kutokana na\(0.58\overline{3}, 0.47, 3.605551275\ldots\) orodha ya nambari

    1. idadi ya busara
    2. idadi irrational.
    Jibu
    1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
    2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
    Zoezi\(\PageIndex{11}\)

    Kwa nambari zilizotolewa orodha

    1. idadi ya busara
    2. nambari zisizo na maana:\(0.29, 0.81\overline{6}, 2.515115111….\)
    Jibu
    1. \(0.29, 0.81\overline{6}\)
    2. \(2.515115111….\)
    Zoezi\(\PageIndex{12}\)

    Kwa nambari zilizotolewa orodha

    1. idadi ya busara
    2. nambari zisizo na maana:\(2.6\overline{3}, 0.125, 0.418302…\)
    Jibu
    1. \(2.6\overline{3}, 0.125\)
    2. \(0.418302…\)
    Zoezi\(\PageIndex{13}\)

    Kwa kila nambari iliyotolewa, tambua ikiwa ni busara au isiyo ya maana:

    1. \(\sqrt{36}\)
    2. \(\sqrt{44}\)
    Jibu
    1. Tambua kwamba 36 ni mraba kamili, tangu\(6^{2} = 36\). Kwa hiyo\(\sqrt{36} = 6\), kwa hiyo\(\sqrt{36}\) ni busara.
    2. Kumbuka kwamba\(6^{2} = 36\) na\(7^{2} = 49\), hivyo\(44\) si mraba kamili. Kwa hiyo, fomu ya decimal ya\(\sqrt{44}\) kamwe kurudia na kamwe kuacha, hivyo\(\sqrt{44}\) ni irrational.
    Zoezi\(\PageIndex{14}\)

    Kwa kila nambari iliyotolewa, tambua ikiwa ni busara au isiyo ya maana:

    1. \(\sqrt{81}\)
    2. \(\sqrt{17}\)
    Jibu
    1. busara
    2. isiyo na maana
    Zoezi\(\PageIndex{15}\)

    Kwa kila nambari iliyotolewa, tambua ikiwa ni busara au isiyo ya maana:

    1. \(\sqrt{116}\)
    2. \(\sqrt{121}\)
    Jibu
    1. isiyo na maana
    2. busara

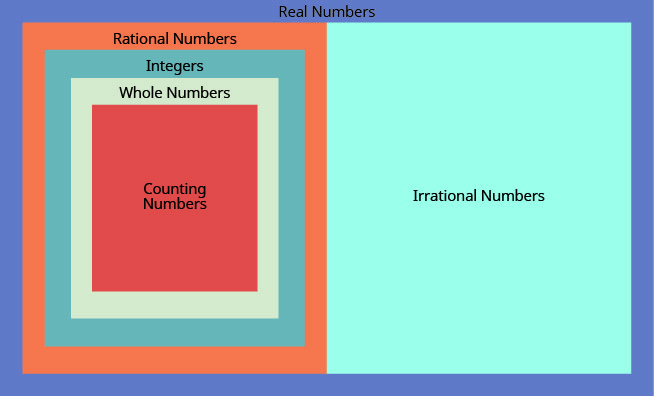
    Tumeona kwamba namba zote za kuhesabu ni namba nzima, namba zote ni integers, na integers zote ni namba za busara. Nambari zisizo na maana ni namba ambazo fomu ya decimal haina kuacha na haina kurudia. Wakati sisi kuweka pamoja idadi ya busara na idadi irrational, sisi kupata seti ya idadi halisi s.

    NAMBARI HALISI

    Nambari halisi ni namba ambayo ni ya busara au isiyo ya maana.

    Nambari zote tunazotumia katika algebra ya msingi ni namba halisi. Kielelezo\(\PageIndex{3}\) unaeleza jinsi seti idadi tumekuwa kujadiliwa katika sehemu hii fit pamoja.

    Takwimu hii ina mchoro wa Venn. Kuanza kuna mstatili mkubwa uliowekwa Hesabu halisi. Nusu ya haki ya mstatili ina Hesabu zisizofaa. Nusu ya kushoto ina Hesabu za busara. Ndani ya mstatili wa Hesabu za Mantiki, kuna integers..., hasi 2, hasi 1, 0, 1, 2,... Ndani ya mstatili wa Integers, kuna Hesabu nzima 0, 1, 2, 3,... Ndani ya mstatili wa Hesabu nzima, kuna Hesabu za Hesabu 1, 2, 3,...
    Kielelezo\(\PageIndex{3}\): Chati hii inaonyesha seti ya idadi ambayo hufanya seti ya namba halisi. Je! Neno “namba halisi” linaonekana kuwa la ajabu kwako? Je, kuna idadi yoyote ambayo si “halisi,” na, ikiwa ni hivyo, inaweza kuwa nini?

    Je, tunaweza kurahisisha\(\sqrt{-25}\)? Je, kuna idadi ambayo mraba ni\(−25\)?

    \[(\quad)^{2}=−25?\]

    Hakuna hata idadi kwamba sisi kushughulikiwa na hadi sasa ina mraba yaani\(−25\). Kwa nini? Nambari yoyote nzuri ya mraba ni chanya. Nambari yoyote mbaya ya mraba ni chanya. Kwa hiyo tunasema hakuna idadi halisi sawa na\(\sqrt{-25}\).

    Mzizi wa mraba wa namba hasi sio namba halisi.

    Zoezi\(\PageIndex{16}\)

    Kwa kila namba iliyotolewa, tambua iwapo ni namba halisi au si namba halisi:

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{64}\)
    Jibu
    1. Hakuna idadi halisi ambayo mraba ni\(−169\). Kwa hiyo,\(\sqrt{-169}\) si idadi halisi.
    2. Kwa kuwa hasi ni mbele ya radical,\(-\sqrt{64}\) ni\(−8\), Tangu\(−8\) ni idadi halisi,\(-\sqrt{64}\) ni idadi halisi.
    Zoezi\(\PageIndex{17}\)

    Kwa kila namba iliyotolewa, tambua iwapo ni namba halisi au si namba halisi:

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{81}\)
    Jibu
    1. si idadi halisi
    2. idadi halisi
    Zoezi\(\PageIndex{18}\)

    Kwa kila namba iliyotolewa, tambua iwapo ni namba halisi au si namba halisi:

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    Jibu
    1. idadi halisi
    2. si idadi halisi
    Zoezi\(\PageIndex{19}\)

    Kutokana na idadi\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), orodha

    1. idadi nzima
    2. namba kamili
    3. idadi ya busara
    4. nambari zisizo na maana
    5. idadi halisi
    Jibu
    1. Kumbuka, namba zote ni 0, 1, 2, 3,... na 8 ni namba nzima pekee iliyotolewa.
    2. Integers ni namba nzima, kinyume chake, na 0. Hivyo idadi nzima 8 ni integer, na -7 ni kinyume cha idadi nzima hivyo ni integer, pia. Pia, angalia kwamba 64 ni mraba wa 8 hivyo\(-\sqrt{64} = -8\). Hivyo integers ni\(−7, 8, \sqrt{64}\).
    3. Kwa kuwa integers zote ni busara, basi\(-7, 8, -\sqrt{64}\) ni busara. Nambari za busara pia zinajumuisha sehemu ndogo na decimals ambazo hurudia au kuacha, hivyo\(\frac{14}{5}\) na\(5.9\) ni busara. Hivyo orodha ya idadi ya busara ni\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
    4. Kumbuka kwamba 5 si mraba kamili, hivyo\(\sqrt{5}\) ni irrational.
    5. Nambari zote zilizoorodheshwa ni namba halisi.
    Zoezi\(\PageIndex{20}\)

    Kwa idadi iliyotolewa, orodha

    1. idadi nzima
    2. namba kamili
    3. idadi ya busara
    4. nambari zisizo na maana
    5. idadi halisi:\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Jibu
    1. \(4, \sqrt{49}\).
    2. \(−3, 4, \sqrt{49}\)
    3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    4. \( -\sqrt{2}\)
    5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Zoezi\(\PageIndex{21}\)

    Kwa idadi iliyotolewa, orodha

    1. idadi nzima
    2. namba kamili
    3. idadi ya busara
    4. nambari zisizo na maana
    5. idadi halisi:\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
    Jibu
    1. \(6, \sqrt{121}\).
    2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
    3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
    4. \(2.041975…\)
    5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

    Pata sehemu ndogo kwenye Mstari wa Idadi

    Mara ya mwisho tuliangalia mstari wa nambari, ilikuwa na integers nzuri na hasi juu yake. Sasa tunataka kuingiza sehemu s na decimals juu yake.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Nambari ya Line Sehemu ya 3” itakusaidia kuendeleza uelewa bora wa eneo la sehemu ndogo kwenye mstari wa nambari.

    Hebu tuanze na sehemu ndogo na upate\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) na\(\frac{8}{3}\) kwenye mstari wa nambari.

    Tutaanza na namba nzima 3 na -5. kwa sababu wao ni rahisi kupanga njama. Angalia Kielelezo\(\PageIndex{4}\).

    Sehemu ndogo zilizoorodheshwa ni\(\frac{1}{5}\text{ and } -\frac{4}{5}\). Tunajua sehemu sahihi\(\frac{1}{5}\) ina thamani chini ya moja na hivyo itakuwa iko kati ya 0 na 1. Denominator ni 5, hivyo tunagawanya kitengo kutoka 0 hadi 1 hadi sehemu 5 sawa\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). Sisi njama\(\frac{1}{5}\). Angalia Kielelezo\(\PageIndex{4}\).

    Vilevile,\(-\frac{4}{5}\) iko kati ya 0 na -1. Baada ya kugawanya kitengo katika sehemu 5 sawa tunapanga njama\(-\frac{4}{5}\). Angalia Kielelezo\(\PageIndex{4}\).

    Hatimaye, angalia sehemu zisizofaa\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). Hizi ni sehemu ndogo ambazo namba ni kubwa kuliko denominator. Kuweka pointi hizi inaweza kuwa rahisi ikiwa utabadilisha kila mmoja kwa namba iliyochanganywa. Angalia Kielelezo\(\PageIndex{4}\).

    \[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

    Kielelezo\(\PageIndex{4}\) kinaonyesha mstari wa nambari na pointi zote zilizopangwa.

    Kuna idadi line umeonyesha kwamba anaendesha kutoka hasi 6 kwa chanya 6. Kutoka kushoto kwenda kulia, namba zilizowekwa alama ni hasi 5, hasi 9/2, hasi 4/5, 1/5, 4/5, 8/3, na 3. Nambari hasi 9/2 ni nusu kati ya hasi 5 na hasi 4. Nambari hasi 4/5 ni kidogo kwa haki ya hasi 1. Nambari 1/5 ni kidogo na haki ya 0. Nambari 4/5 ni kidogo upande wa kushoto wa 1. Nambari 8/3 ni kati ya 2 na 3, lakini karibu kidogo na 3.
    Kielelezo\(\PageIndex{4}\)
    Zoezi\(\PageIndex{22}\)

    Machapisho na studio yafuatayo kwenye mstari namba:\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) na\(\frac{7}{3}\).

    Jibu

    Machapisho na njama integers, 4, 1-3.

    Pata sehemu sahihi\(\frac{3}{4}\) kwanza. Sehemu\(\frac{3}{4}\) ni kati ya 0 na 1. Gawanya umbali kati ya 0 na 1 katika sehemu nne sawa basi, tunapanga njama\(\frac{3}{4}\). Vile vile njama\(-\frac{1}{4}\).

    Sasa Pata sehemu zisizofaa\(\frac{6}{5}\),\(-\frac{5}{2}\),\(\frac{7}{3}\). Ni rahisi kuwapanga njama ikiwa tunawabadilisha kwa nambari zilizochanganywa na kisha kuzipanga kama ilivyoelezwa hapo juu:\(\frac{6}{5} = 1\frac{1}{5}\),\(-\frac{5}{2} = -2\frac{1}{2}\),\(\frac{7}{3} = 2\frac{1}{3}\).

    Kuna idadi line umeonyesha kwamba anaendesha kutoka hasi 6 kwa chanya 6. Kutoka kushoto kwenda kulia, namba zilizowekwa alama ni hasi 3, hasi 5/2, hasi 1/4, 3/4, 6/5, 7/3, na 4. Nambari hasi 5/2 ni nusu kati ya hasi 3 na hasi 2. Nambari hasi 1/4 ni kidogo upande wa kushoto wa 0. Nambari 3/4 ni kidogo upande wa kushoto wa 1. Nambari 6/5 ni kidogo kwa haki ya 1. Nambari 7/3 ni kati ya 2 na 3, lakini karibu kidogo na 2.

    Zoezi\(\PageIndex{23}\)

    Machapisho na studio yafuatayo kwenye mstari namba:\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) na\(-\frac{8}{3}\).

    Jibu

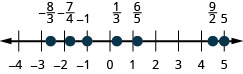
    Kuna idadi line umeonyesha kwamba anaendesha kutoka hasi 4 kwa chanya 5. Kutoka kushoto kwenda kulia, namba zilizowekwa alama ni hasi 8/3, hasi 7/4, hasi 1, 1/3, 6/5, 9/2, na 5. Nambari hasi 8/3 ni kati ya hasi 3 na hasi 2 lakini karibu kidogo na hasi 3. Nambari hasi 7/4 ni kidogo kwa haki ya hasi 2. Nambari 1/3 ni kidogo kwa haki ya 0. Nambari 6/5 ni kidogo kwa haki ya 1. Nambari 9/2 ni nusu kati ya 4 na 5.

    Zoezi\(\PageIndex{24}\)

    Machapisho na studio yafuatayo kwenye mstari namba:\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) na\(\frac{8}{3}\).

    Jibu

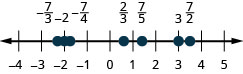
    Kuna idadi line umeonyesha kwamba anaendesha kutoka hasi 4 kwa chanya 5. Kutoka kushoto kwenda kulia, namba zilizowekwa alama ni hasi 7/3, hasi 2, hasi 7/4, 2/3, 7/5, 3, na 7/2. Nambari hasi 7/3 ni kati ya hasi 3 na hasi 2 lakini karibu kidogo na hasi 2. Nambari hasi 7/4 ni kidogo kwa haki ya hasi 2. Nambari 2/3 ni kidogo upande wa kushoto wa 1. Nambari 7/5 ni kati ya 1 na 2, lakini karibu na 1. Nambari 7/2 ni nusu kati ya 3 na 4.

    Katika Zoezi\(\PageIndex{25}\), tutaweza kutumia alama kukosekana kwa usawa ili sehemu ndogo. Katika sura zilizopita tulitumia mstari wa nambari ili namba.

    • \(a < b\)“a ni chini ya b” wakati a ni upande wa kushoto wa b kwenye mstari wa namba
    • \(a > b\)“a ni kubwa kuliko b” wakati a ni haki ya b kwenye mstari wa namba

    Tunapohamia kutoka kushoto kwenda kulia kwenye mstari wa nambari, maadili huongezeka.

    Zoezi\(\PageIndex{25}\)

    Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\). Inaweza kuwa na manufaa kwa rejea Kielelezo\(\PageIndex{5}\).

    1. \(−\frac{2}{3}\text{___}-1\)
    2. \(−3\frac{1}{2}\text{___}-3\)
    3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
    4. \(−2\text{___}-\frac{8}{3}\)
    Kuna idadi line umeonyesha kwamba anaendesha kutoka hasi 4 kwa chanya 4. Kutoka kushoto kwenda kulia, namba zilizowekwa alama ni hasi 3 na 1/2, hasi 3, hasi 8/3, hasi 2, hasi 1, hasi 3/4, hasi 2/3, na 1/4 hasi. Nambari hasi 3 na 1/2 ni kati ya hasi 4 na hasi 3 Nambari hasi 8/3 ni kati ya hasi 3 na hasi 2, lakini karibu na hasi 3. Nambari hasi 3/4, hasi 2/3, na hasi 1/4 zote ni kati ya hasi 1 na 0.
    Kielelezo\(\PageIndex{5}\)
    Jibu

    Kuwa makini wakati wa kuagiza namba hasi.

    1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
    4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
    Zoezi\(\PageIndex{26}\)

    Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\).

    1. \(−\frac{1}{3}\text{___}-1\)
    2. \(−1\frac{1}{2}\text{___}-2\)
    3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
    4. \(−3\text{___}-\frac{7}{3}\)
    Jibu
    1. \(>\)
    2. \(>\)
    3. \(<\)
    4. \(<\)
    Zoezi\(\PageIndex{27}\)

    Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\).

    1. \(−1\text{___}-\frac{2}{3}\)
    2. \(−2\frac{1}{4}\text{___}-2\)
    3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
    4. \(−4\text{___}-\frac{10}{3}\)
    Jibu
    1. \(<\)
    2. \(<\)
    3. \(>\)
    4. \(<\)

    Pata Decimals kwenye Mstari wa Idadi

    Kwa kuwa decimals ni aina ya sehemu ndogo, kupata decimals kwenye mstari wa nambari ni sawa na kupata sehemu ndogo kwenye mstari wa namba.

    Zoezi\(\PageIndex{28}\)

    Pata 0.4 kwenye mstari wa nambari.

    Jibu

    Sehemu sahihi ina thamani chini ya moja. Nambari ya decimal\(0.4\) ni sawa na, sehemu sahihi, hivyo\(0.4\) iko kati ya 0 na 1.\(\frac{4}{10}\) Kwenye mstari wa nambari, fungua muda kati ya 0 na 1 hadi sehemu 10 sawa. Sasa lebo sehemu\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). Tunaandika 0 kama 0.0 na 1 na 1.0, ili idadi ni mara kwa mara katika sehemu ya kumi. Hatimaye, alama\(0.4\) kwenye mstari wa namba. Angalia Kielelezo\(\PageIndex{6}\).

    Kuna idadi line umeonyesha kwamba anaendesha kutoka 0.0 kwa 1. Hatua pekee iliyotolewa ni 0.4, ambayo ni kati ya 0.3 na 0.5.
    Kielelezo\(\PageIndex{6}\)
    Zoezi\(\PageIndex{29}\)

    Pata kwenye mstari wa nambari: 0.6.

    Jibu

    Kuna idadi line umeonyesha kwamba anaendesha kutoka 0.0 kwa 1. Hatua pekee iliyotolewa ni 0.6, ambayo ni kati ya 0.5 na 0.7.

    Zoezi\(\PageIndex{30}\)

    Pata kwenye mstari wa nambari: 0.9.

    Jibu

    Kuna idadi line umeonyesha kwamba anaendesha kutoka 0.0 kwa 1. Hatua pekee iliyotolewa ni 0.9, ambayo ni kati ya 0.8 na 1.

    Zoezi\(\PageIndex{31}\)

    Pata\(−0.74\) kwenye mstari wa nambari.

    Jibu

    Decimal (-0.74\) ni sawa na\(-\frac{74}{100}\), hivyo iko kati ya 0 na -1. Kwenye mstari wa nambari, alama na uandike alama ya hundredths katika muda kati ya 0 na -1. Angalia Kielelezo\(\PageIndex{7}\).

    Kuna namba line umeonyesha kwamba anaendesha kutoka hasi 1.00 kwa 0.00. Hatua pekee iliyotolewa ni hasi 0.74, ambayo ni kati ya hasi 0.8 na hasi 0.7.
    Kielelezo\(\PageIndex{7}\)
    Zoezi\(\PageIndex{32}\)

    Pata kwenye mstari wa nambari: -0.6.

    Jibu

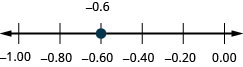
    Kuna namba line umeonyesha kwamba anaendesha kutoka hasi 1.00 kwa 0.00. Hatua pekee iliyotolewa ni hasi 0.6, ambayo ni kati ya hasi 0.8 na hasi 0.4.

    Zoezi\(\PageIndex{33}\)

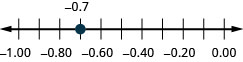
    Pata kwenye mstari wa nambari: -0.7.

    Jibu

    Kuna namba line umeonyesha kwamba anaendesha kutoka hasi 1.00 kwa 0.00. Hatua pekee iliyotolewa ni hasi 0.7, ambayo ni kati ya hasi 0.8 na hasi 0.6.

    Ambayo ni kubwa, 0.04 au 0.40? Ikiwa unafikiria hili kama pesa, unajua kwamba $0.40 (senti arobaini) ni kubwa kuliko $0.04 (senti nne). Hivyo,\(0.40 > 0.04\)

    Tena, tunaweza kutumia mstari namba ili namba.

    • \(a < b\)“a ni chini ya b” wakati a ni upande wa kushoto wa b kwenye mstari wa namba
    • \(a > b\)“a ni kubwa kuliko b” wakati a ni haki ya b kwenye mstari wa namba

    Wapi 0.04 na 0.40 iko kwenye mstari wa namba? Angalia Kielelezo\(\PageIndex{8}\).

    Kuna mstari wa nambari unaoonyeshwa unaoendesha kutoka hasi 0.0 hadi 1.0. Kutoka kushoto kwenda kulia, kuna pointi 0.04 na 0.4 alama. Hatua 0.04 ni kati ya 0.0 na 0.1. Hatua 0.4 ni kati ya 0.3 na 0.5.
    Kielelezo\(\PageIndex{8}\)

    Tunaona kwamba 0.40 ni haki ya 0.04 kwenye mstari wa namba. Hii ni njia nyingine ya kuonyesha kwamba\(0.40 > 0.04\).

    Je, 0.31 inalinganishaje na 0.308? Hii haina kutafsiri katika fedha ili iwe rahisi kulinganisha. Lakini kama sisi kubadilisha 0.31 na 0.308 katika sehemu ndogo, tunaweza kuwaambia ambayo ni kubwa.

      0.31 0.308
    Badilisha kwa sehemu ndogo. \(\frac{31}{100}\) \(\frac{308}{1000}\)
    Tunahitaji denominator ya kawaida ili kulinganisha nao. . .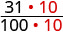
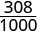      \(\frac{310}{1000}\) \(\frac{308}{1000}\)
    Jedwali\(\PageIndex{2}\)

    Kwa sababu\(310 > 308\), tunajua kwamba\(\frac{310}{1000} > \frac{308}{1000}\). Kwa hiyo,\(0.31 > 0.308\).

    Angalia kile\(\frac{310}{1000}\) tulichofanya katika\(0.31\) kuwabadili sehemu - tulianza na sehemu\(\frac{31}{100}\) na kumalizika kwa sehemu sawa. Kubadili\(\frac{310}{1000}\) nyuma kwa decimal inatoa 0.310. Hivyo 0.31 ni sawa na 0.310. Kuandika zero mwishoni mwa decimal haubadili thamani yake!

    \[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

    Tunasema 0.31 na 0.310 ni decimals sawa.

    DESIMALS SAWA

    Decimals mbili ni sawa kama wao kubadilisha kwa sehemu sawa.

    Tunatumia decimals sawa wakati sisi ili decimals.

    Hatua tunazochukua ili kuagiza decimals zimefupishwa hapa.

    ILI DESIMALS.
    1. Andika namba moja chini ya nyingine, ukiweka pointi za decimal.
    2. Angalia ili uone kama namba zote mbili zina idadi sawa ya tarakimu. Ikiwa sio, weka zero mwishoni mwa moja na tarakimu chache ili kuwafanya mechi.
    3. Linganisha namba kama zilikuwa namba nzima.
    4. Amri namba kwa kutumia ishara sahihi ya usawa.
    Zoezi\(\PageIndex{34}\)

    Agizo\(0.64 \text{ ___ } 0.6\) kutumia\(<\) au\(>\).

    Jibu

    \(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

    Zoezi\(\PageIndex{35}\)

    Agizo kila moja ya jozi zifuatazo za namba, kutumia\(<\) au\(>\):\(0.42 \text{ ___ } 0.4\).

    Jibu

    \(>\)

    Zoezi\(\PageIndex{36}\)

    Agizo kila moja ya jozi zifuatazo za namba, kutumia\(<\) au\(>\):\(0.18 \text{ ___ } 0.1\).

    Jibu

    \(>\)

    Zoezi\(\PageIndex{37}\)

    Agizo\(0.83 \text{ ___ } 0.803\) kutumia\(<\) au\(>\).

    Jibu

    \(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

    Zoezi\(\PageIndex{38}\)

    Agizo kila moja ya jozi zifuatazo za namba, kutumia\(<\) au\(>\):\(0.76 \text{ ___ } 0.706\).

    Jibu

    \(>\)

    Zoezi\(\PageIndex{39}\)

    Agizo kila moja ya jozi zifuatazo za namba, kutumia\(<\) au\(>\):\(0.305 \text{ ___ } 0.35\).

    Jibu

    \(<\)

    Tunapoagiza decimals hasi, ni muhimu kukumbuka jinsi ya kuagiza integers hasi. Kumbuka kwamba idadi kubwa ni na haki juu ya mstari idadi. Kwa mfano, kwa sababu -2 iko na haki ya -3 kwenye mstari wa namba, tunajua hilo\(−2>−3\). Vile vile, idadi ndogo hulala upande wa kushoto kwenye mstari wa nambari. Kwa mfano, kwa sababu -9 iko upande wa kushoto wa -6 kwenye mstari wa namba, tunajua hilo\(−9<−6\). Angalia Kielelezo\(\PageIndex{9}\).

    Kuna idadi line umeonyesha kwamba anaendesha kutoka hasi 10 kwa 0. Hakuna pointi zilizotolewa na hashmarks zipo katika kila integer kati ya hasi 10 na 0.
    Kielelezo\(\PageIndex{9}\)

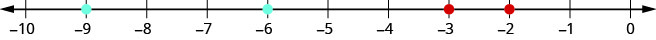
    Kama sisi zoomed katika juu ya muda kati ya 0 na -1, kama inavyoonekana katika Zoezi\(\PageIndex{40}\), tutakuwa kuona kwa njia sawa kwamba\(−0.2>−0.3\) na\(−0.9<−0.6\).

    Zoezi\(\PageIndex{40}\)

    Tumia\(<\) au\(>\) utaratibu\(−0.1\text{ ___ }−0.8\).

    Jibu

    \(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

    Zoezi\(\PageIndex{41}\)

    Agizo jozi zifuatazo za namba, kutumia\(<\) au\(>\):\(−0.3\text{ ___ }−0.5\).

    Jibu

    \(>\)

    Zoezi\(\PageIndex{42}\)

    Agizo jozi zifuatazo za namba, kutumia\(<\) au\(>\):\(−0.6\text{ ___ }−0.7\).

    Jibu

    \(>\)

    Dhana muhimu

    • Square Root Nukuu
      \(\sqrt{m}\) ni kusoma 'mizizi mraba ya\(m\). ' Ikiwa\(m = n^{2}\), basi\(\sqrt{m} = n\), kwa\(n \geq 0\).
    • Order Desimals
      1. Andika namba moja chini ya nyingine, ukiweka pointi za decimal.
      2. Angalia ili uone kama namba zote mbili zina idadi sawa ya tarakimu. Ikiwa sio, weka zero mwishoni mwa moja na tarakimu chache ili kuwafanya mechi.
      3. Linganisha namba kama zilikuwa namba nzima.
      4. Amri namba kwa kutumia ishara sahihi ya usawa.

    Mazoezi hufanya kamili

    Punguza Maneno na Mizizi ya Mraba

    Katika mazoezi yafuatayo, kurahisisha.