Skip to main content
Global

1.6: Tazama sehemu ndogo

  1. Last updated
  2. Save as PDF
  • Page ID
    177997

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Pata sehemu ndogo sawa
    • Kurahisisha sehemu
    • Kuzidisha vipande
    • Gawanya vipande
    • Kurahisisha maneno yaliyoandikwa na bar ya sehemu
    • Tafsiri misemo kwa maneno na sehemu ndogo
    Kumbuka

    Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sehemu hii inaweza kupatikana katika sura ya Prealgebra, Sehemu ndogo.

    Pata FRACTIONS sawa

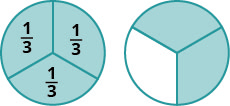
    Sehemu ndogo ni njia ya kuwakilisha sehemu nzima. Sehemu\(\dfrac{1}{3}\) ina maana kwamba nzima imegawanywa katika sehemu tatu sawa na kila sehemu ni moja ya sehemu tatu sawa. Angalia Kielelezo\(\PageIndex{1}\). Sehemu\(\dfrac{2}{3}\) inawakilisha sehemu mbili za tatu sawa. Katika sehemu\(\dfrac{2}{3}\), 2 inaitwa nambari na 3 inaitwa denominator.

    Duru mbili zinaonyeshwa, kila mmoja imegawanywa katika vipande vitatu sawa na mistari. Mzunguko wa mkono wa kushoto umeandikwa “theluthi moja” katika kila sehemu. Kila sehemu ni kivuli. Mduara upande wa kulia umevuliwa katika sehemu mbili za tatu.
    Kielelezo\(\PageIndex{1}\): Mduara upande wa kushoto umegawanywa katika sehemu tatu sawa. Kila sehemu ni\(\dfrac{1}{3}\) ya 3 sehemu sawa. Katika mduara upande wa kulia,\(\frac{2}{3}\) wa mduara ni kivuli (2 ya 3 sehemu sawa).
    Kufanya shughuli za Hisabati za Manipulative “Sehemu za Mfano” zitakusaidia kuendeleza uelewa bora wa vipande vipande, nambari zao na denominators.
    SEHEMU

    Sehemu imeandikwa\(\dfrac{a}{b}\), wapi\(b\neq 0\) na

    • \(a\)ni nambari na\(b\) ni denominator.

    Sehemu inawakilisha sehemu ya nzima. Denominator\(b\) ni idadi ya sehemu sawa ambazo zote zimegawanywa, na namba\(a\) inaonyesha sehemu ngapi zinajumuishwa.

    Ikiwa pie nzima imekatwa vipande 6 na tunakula vipande vyote 6, tulikula\(\dfrac{6}{6}\) vipande, au, kwa maneno mengine, pie moja nzima.

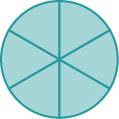
    Mduara unaonyeshwa na umegawanywa katika sehemu sita. Sehemu zote zimefunikwa.
    Kielelezo\(\PageIndex{2}\)

    Hivyo\(\dfrac{6}{6}=1\). Hii inatuongoza kwenye mali ya moja ambayo inatuambia kwamba idadi yoyote, isipokuwa sifuri, imegawanywa na yenyewe ni\(1\).

    MALI YA MOJA

    \[\dfrac{a}{a} = 1 \quad (a \neq 0)\]

    Nambari yoyote, isipokuwa sifuri, imegawanywa na yenyewe ni moja.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Fractions sawa na One” itakusaidia kuendeleza uelewa bora wa vipande ambavyo ni sawa na moja.

    Ikiwa pie ilikatwa vipande 6 na tulikula kila 6, tulikula\(\dfrac{6}{6}\) vipande, au, kwa maneno mengine, pie moja nzima. Ikiwa pie ilikatwa vipande 8 na tulikula yote 8, tulikula\(\dfrac{8}{8}\) vipande, au pie moja nzima. Tulikula kiasi sawa—pie moja nzima.

    Sehemu ndogo\(\dfrac{6}{6}\) na\(\dfrac{8}{8}\) kuwa na thamani sawa, 1, na hivyo huitwa sehemu ndogo sawa. Sehemu ndogo sawa ni sehemu ndogo ambazo zina thamani sawa.

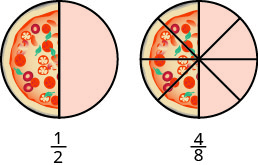
    Hebu fikiria pizzas wakati huu. Kielelezo\(\PageIndex{3}\) kinaonyesha picha mbili: pizza moja upande wa kushoto, kata vipande viwili sawa, na pizza ya pili ya ukubwa sawa, kata vipande nane upande wa kulia. Hii ni njia ya kuonyesha kwamba\(\dfrac{1}{2}\) ni sawa na\(\dfrac{4}{8}\). Kwa maneno mengine, wao ni sehemu ndogo sawa.

    Mduara unaonyeshwa kuwa umegawanywa katika wedges nane sawa na mistari. Upande wa kushoto wa mduara ni pizza yenye sehemu nne zinazounda vipande vya pizza. Upande wa kulia una sehemu nne za kivuli. Chini ya mchoro ni sehemu nne za nane.
    Kielelezo\(\PageIndex{3}\): Kwa kuwa kiasi hicho ni ya kila pizza ni kivuli, tunaona kwamba\(\dfrac{1}{2}\) ni sawa na\(\dfrac{4}{8}\). Wao ni sehemu ndogo sawa.
    VIPANDE SAWA

    Sehemu ndogo sawa ni sehemu ndogo ambazo zina thamani sawa.

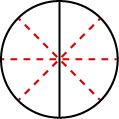
    Tunawezaje kutumia hisabati kubadili\(\dfrac{1}{2}\)\(\dfrac{4}{8}\)? Tunawezaje kuchukua pizza iliyokatwa vipande viwili na kuikata vipande 8? Tunaweza kukata kila moja ya 2 vipande kubwa katika 4 vipande vidogo! Pizza nzima ingekuwa kisha kukatwa vipande 88 badala ya 2 tu. Kihisabati, nini tumekuwa ilivyoelezwa inaweza kuandikwa kama hii kama\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\). Angalia Kielelezo\(\PageIndex{4}\).

    Mduara unaonyeshwa na umegawanywa kwa nusu na mstari mweusi wa wima. Imegawanywa zaidi katika nane kwa kuongezea mistari nyekundu yenye rangi nyekundu.
    Kielelezo\(\PageIndex{4}\): Kukata kila nusu ya pizza katika vipande 4, hutupa pizza kukatwa vipande 8:\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\)

    Mfano huu unasababisha mali ifuatayo:

    SAWA FRACTIONS MALI

    Ikiwa\(a,b,c\) ni idadi ambapo\(b\neq 0, c\neq 0\), basi

    \[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]

    Kama tulikuwa kukata pizza tofauti, tunaweza kupata

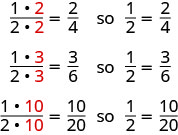
    Picha inaonyesha safu tatu za sehemu ndogo. Katika mstari wa kwanza ni sehemu ndogo “1, mara 2, imegawanywa na 2, mara 2, sawa na nne mbili”. Karibu na hili ni neno “hivyo” na sehemu “nusu moja, sawa na nne mbili. Mstari wa pili unasoma “1, mara 3, imegawanywa na mara 2 3, sawa na sita tatu”. Karibu na hili ni neno “hivyo” na sehemu “nusu moja sawa, sita sita”. Mstari wa tatu unasoma “mara 1 10, imegawanywa na mara 2 10, kumi ya ishirini”. Karibu na hili ni neno “hivyo” na sehemu “nusu moja sawa, ishirini kumi”.
    Kielelezo\(\PageIndex{5}\)

    Kwa hiyo, tunasema\(\dfrac{1}{2}\)\(\dfrac{2}{4}\),,\(\dfrac{3}{6}\), na\(\dfrac{10}{20}\) ni sehemu ndogo sawa.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Sehemu sawa” zitakusaidia kuendeleza uelewa bora wa maana yake wakati sehemu mbili ni sawa.

    Zoezi\(\PageIndex{1}\)

    Kupata sehemu tatu sawa na\(\dfrac{2}{5}\).

    Jibu

    Ili kupata sehemu sawa na\(\dfrac{2}{5}\), tunazidisha nambari na denominator kwa idadi sawa. Tunaweza kuchagua nambari yoyote, ila kwa sifuri. Hebu tuwazidishe kwa 2, 3, na kisha 5.

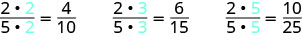
    Mstari wa sehemu ndogo husoma “mara 2, imegawanywa na mara 5 2, sawa na nne kumi”. Karibu na hii ni “2, mara 3, imegawanywa na mara 5 3, sawa na sita kumi na tano”. Karibu na hii ni “mara 2 5, imegawanywa na mara 5 5, sawa na kumi ishirini na tano”.

    Hivyo,\(\dfrac{4}{10}\),\(\dfrac{6}{15}\), na\(\dfrac{10}{25}\) ni sawa na\(\dfrac{2}{5}\).

    Zoezi\(\PageIndex{2}\)

    Kupata sehemu tatu sawa na\(\dfrac{3}{5}\).

    Jibu

    \(\dfrac{6}{10}\),\(\dfrac{9}{15}\),\(\dfrac{12}{20}\); majibu yanaweza kutofautiana

    Zoezi\(\PageIndex{3}\)

    Kupata sehemu tatu sawa na\(\dfrac{4}{5}\).

    Jibu

    \(\dfrac{8}{10}\),\(\dfrac{12}{15}\),\(\dfrac{16}{20}\); majibu yanaweza kutofautiana

    Kurahisisha Fractions

    Sehemu inachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida, isipokuwa 1, katika nambari yake na denominator.

    Kwa mfano,

    • \(\dfrac{2}{3}\)ni rahisi kwa sababu hakuna sababu ya kawaida ya 2 na 3.
    • \(\dfrac{10}{15}\)si rahisi kwa sababu 5 ni sababu ya kawaida ya 10 na 15.
    SEHEMU RAHISI

    Sehemu inachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida katika nambari yake na denominator.

    Maneno hupunguza sehemu ina maana ya kurahisisha sehemu. Sisi kurahisisha, au kupunguza, sehemu kwa kuondoa mambo ya kawaida ya nambari na denominator. Sehemu haijarahisishwa mpaka mambo yote ya kawaida yameondolewa. Ikiwa maneno yana sehemu ndogo, sio rahisi kabisa mpaka sehemu ndogo zimefunguliwa.

    Katika Zoezi\(\PageIndex{4}\), sisi kutumika sawa FRACTIONS mali kupata FRACTIONS sawa. Sasa tutaweza kutumia sawa FRACTIONS mali katika reverse kurahisisha FRACTIONS. Tunaweza kuandika upya mali ili kuonyesha fomu zote mbili pamoja.

    SAWA FRACTIONS MALI

    Kama\(a,b,c\) ni idadi ambapo\(b\neq 0,c\neq 0\),

    \[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]

    Zoezi\(\PageIndex{4}\)

    Kurahisisha:\(-\dfrac{32}{56}\)

    Jibu
      \(-\dfrac{32}{56}\)
    Andika upya nambari na denominator kuonyesha mambo ya kawaida. \(-\dfrac{4\cdot 8}{7\cdot 8}\)
    Kurahisisha kutumia sawa FRACTIONS mali. \(-\dfrac{4}{7}\)

    Angalia kwamba sehemu\(-\dfrac{4}{7}\) ni rahisi kwa sababu hakuna mambo ya kawaida zaidi.

    Zoezi\(\PageIndex{5}\)

    Kurahisisha:\(-\dfrac{42}{54}\)

    Jibu

    \(-\dfrac{7}{9}\)

    Zoezi\(\PageIndex{6}\)

    Kurahisisha:\(-\dfrac{42}{54}\)

    Jibu

    \(-\dfrac{5}{9}\)

    Wakati mwingine inaweza kuwa si rahisi kupata mambo ya kawaida ya nambari na denominator. Wakati hii itatokea, wazo nzuri ni sababu nambari na denominator katika idadi mkuu s Kisha kugawanya mambo ya kawaida kwa kutumia sawa sehemu ya mali.

    Zoezi\(\PageIndex{7}\)

    Kurahisisha:\(-\dfrac{210}{385}\)

    Jibu

    Jedwali linaonyeshwa na nguzo tatu na safu tatu. Mstari wa kwanza wa safu ya kushoto unasoma “Hatua ya 1. Andika upya nambari na denominator ili kuonyesha mambo ya kawaida. Ikiwa inahitajika, tumia mti wa sababu”. Karibu na hili katika safu ya kati, inasoma “upya upya 210 na 285 kama bidhaa ya primes. Karibu na hili katika safu ya kulia, inasoma “hasi 210 imegawanywa na 385.” Chini ya hii, ni equation “mara mbili mara tatu mara tano saba.” Ya tano na 7 ni bluu na nyekundu kwa mtiririko huo.Mstari uliofuata chini unasoma “Hatua ya 2. Kurahisisha kutumia sawa fractions mali kwa kugawa nje mambo ya kawaida.” Karibu na hili katika safu ya kati, inasoma, “Weka mambo ya kawaida 5 na 7.” Karibu na hili katika safu ya kulia, ina equation mara 2, mara tatu tano, mara saba zaidi ya mara 5 mara saba 11. Wote 5 na 7 wamevuka kama mambo ya kawaida. Chini ya hii ni equation “hasi mara mbili 3 kugawanywa na 11.”Mstari unaofuata unasoma, “Hatua ya 3. Panua mambo yaliyobaki, ikiwa ni lazima.” Karibu na hili katika safu ya kulia ni hasi kumi na sita.

    Zoezi\(\PageIndex{8}\)

    Kurahisisha:\(-\dfrac{69}{120}\)

    Jibu

    \(-\dfrac{23}{40}\)

    Zoezi\(\PageIndex{9}\)

    Kurahisisha:\(-\dfrac{120}{192}\)

    Jibu

    \(-\dfrac{5}{8}\)

    Sasa tunafupisha hatua unazopaswa kufuata ili kurahisisha sehemu ndogo.

    KURAHISISHA SEHEMU.
    1. Andika upya nambari na denominator ili kuonyesha mambo ya kawaida.
      Ikiwa inahitajika, fikiria namba na denominator katika namba za kwanza kwanza.
    2. Kurahisisha kutumia sawa FRACTIONS mali kwa kugawa nje mambo ya kawaida.
    3. Panua mambo yoyote iliyobaki, ikiwa inahitajika.
    Zoezi\(\PageIndex{10}\)

    Kurahisisha:\(\dfrac{5x}{5y}\)

    Jibu
      \(\dfrac{5x}{5y}\)
    Andika upya kuonyesha mambo ya kawaida, kisha ugawanye mambo ya kawaida. .
    Kurahisisha.

    \(\dfrac{x}{y}\)
    Zoezi\(\PageIndex{11}\)

    Kurahisisha:\(\dfrac{7x}{7y}\)

    Jibu

    \(\dfrac{x}{y}\)

    Zoezi\(\PageIndex{12}\)

    Kurahisisha:\(\dfrac{3a}{3b}\)

    Jibu

    \(\dfrac{a}{b}\)

    Kuzidisha vipande

    Watu wengi hupata kuzidisha na kugawa sehemu ndogo rahisi kuliko kuongeza na kuondoa sehemu ndogo. Kwa hiyo tutaanza na kuzidisha sehemu.

    Kufanya shughuli za Hisabati za Manipulative “Kuzidisha Fraction Model” itasaidia kuendeleza uelewa bora wa kuzidisha sehemu ndogo.

    Tutatumia mfano ili kukuonyesha jinsi ya kuzidisha sehemu mbili na kukusaidia kukumbuka utaratibu. Hebu tuanze na\(\dfrac{3}{4}\).

    Mstatili ulioundwa na mraba nne mfululizo. Mraba mitatu ya kwanza ni kivuli.
    Kielelezo\(\PageIndex{6}\)

    Sasa tutaweza kuchukua\(\dfrac{1}{2}\) ya\(\dfrac{3}{4}\).

    Mstatili ulioundwa na mraba nne mfululizo. Mraba mitatu ya kwanza ni kivuli. Nusu ya chini ya mraba mitatu ya kwanza ni kivuli nyeusi na mistari ya diagonal.
    Kielelezo\(\PageIndex{6}\)

    Angalia kwamba sasa, yote imegawanywa katika sehemu 8 sawa. Hivyo\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).

    Ili kuzidisha sehemu ndogo, tunazidisha nambari na kuzidisha denominators.

    KUZIDISHA SEHEMU

    Ikiwa\(a,b,c\) na\(d\) ni namba wapi\(b\neq 0\) na\(d\neq 0\), basi

    \[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]

    Ili kuzidisha sehemu ndogo, kuzidisha nambari na kuzidisha denominators.

    Wakati wa kuzidisha sehemu ndogo, mali ya nambari nzuri na hasi bado hutumika, bila shaka. Ni wazo nzuri kuamua ishara ya bidhaa kama hatua ya kwanza. Katika Zoezi\(\PageIndex{13}\), tutazidisha hasi na chanya, hivyo bidhaa itakuwa hasi.

    Zoezi\(\PageIndex{13}\)

    Kuzidisha:\(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)

    Jibu

    Hatua ya kwanza ni kupata ishara ya bidhaa. Kwa kuwa ishara ni tofauti, bidhaa ni hasi.

    \[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]

    Zoezi\(\PageIndex{14}\)

    Kuzidisha:\(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)

    Jibu

    \(-\dfrac{4}{21}\)

    Zoezi\(\PageIndex{15}\)

    Kuzidisha:\(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)

    Jibu

    \(-\dfrac{3}{16}\)

    Wakati wa kuzidisha sehemu kwa integer, inaweza kuwa na manufaa kuandika integer kama sehemu. integer yoyote, a, inaweza kuandikwa kama\(\dfrac{a}{1}\). Kwa hiyo, kwa mfano,\(3 = \dfrac{3}{1}\).

    Zoezi\(\PageIndex{16}\)

    Kuzidisha:\(-\dfrac{12}{5}(-20x)\)

    Jibu

    Tambua ishara ya bidhaa. Ishara ni sawa, hivyo bidhaa ni chanya.

      \(-\dfrac{12}{5}(-20x)\)
    Andika\(20x\) kama sehemu. \(\dfrac{12}{5}(\dfrac{20x}{1})\)
    Kuzidisha.  
    Andika upya\(20\) ili kuonyesha jambo la kawaida\(5\) na ugawanye. .
    Kurahisisha. \(48x\)
    Zoezi\(\PageIndex{17}\)

    Kuzidisha:\(\dfrac{11}{3}(-9a)\)

    Jibu

    \(-33a\)

    Zoezi\(\PageIndex{18}\)

    Kuzidisha:\(\dfrac{13}{7}(-14b)\)

    Jibu

    \(-26b\)

    Gawanya FRACTIONS

    Sasa kwa kuwa tunajua jinsi ya kuzidisha sehemu ndogo, sisi ni karibu tayari kugawanya. Kabla tunaweza kufanya hivyo, kwamba tunahitaji baadhi ya msamiati.

    Upungufu wa sehemu hupatikana kwa inverting sehemu, kuweka namba katika denominator na denominator katika nambari. Usawa wa\(\dfrac{2}{3}\) ni\(\dfrac{3}{2}\).

    Kumbuka kwamba\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). Nambari na kurudi kwake huongezeka kwa\(1\).

    Ili kupata bidhaa ya chanya\(1\) wakati wa kuzidisha namba mbili, namba lazima ziwe na ishara sawa. Hivyo kurudia lazima iwe na ishara sawa.

    Usawa wa\(-\dfrac{10}{7}\) ni\(-\dfrac{7}{10}\), tangu\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).

    KURUDI

    Usawa wa\(\dfrac{a}{b}\) ni\(\dfrac{b}{a}\).

    Nambari na kuongezeka kwake kwa moja\(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Division Fraction Division” itasaidia kuendeleza uelewa bora wa kugawa sehemu ndogo.

    Ili kugawanya sehemu ndogo, tunazidisha sehemu ya kwanza kwa usawa wa pili.

    SEHEMU MGAWANYIKO

    Ikiwa\(a,b,c\) na\(d\) ni namba wapi\(b\neq 0, c\neq 0\) na\(d\neq 0\), basi

    \[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]

    Ili kugawanya sehemu ndogo, tunazidisha sehemu ya kwanza kwa usawa wa pili.

    Tunahitaji kusema\(b\neq 0, c\neq 0\) na kuwa\(d\neq 0\) na uhakika hatugawanya na sifuri!

    Zoezi\(\PageIndex{19}\)

    Gawanya:\(-\dfrac{2}{3}\div\dfrac{n}{5}\)

    Jibu

    \[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]

    Zoezi\(\PageIndex{20}\)

    Gawanya:\(-\dfrac{3}{5}\div\dfrac{p}{7}\).

    Jibu

    \(-\dfrac{21}{5p}\)

    Zoezi\(\PageIndex{21}\)

    Gawanya:\(-\dfrac{5}{8}\div\dfrac{q}{3}\).

    Jibu

    \(-\dfrac{15}{8q}\)

    Zoezi\(\PageIndex{22}\)

    Pata quotient:

    \(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)

    Jibu
      \(-\dfrac{7}{18}\div(-\dfrac{14}{27})\)
    Ili kugawanya, kuzidisha sehemu ya kwanza kwa usawa wa pili. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\)
    Kuamua ishara ya bidhaa, na kisha uongeze.. \(\dfrac{7\cdot 27}{18\cdot 14}\)
    Andika upya kuonyesha mambo ya kawaida. .
    Ondoa mambo ya kawaida. \(\dfrac{3}{2\cdot 2}\)
    Kurahisisha. \(\dfrac{3}{4}\)
    Zoezi\(\PageIndex{23}\)

    Pata quotient:

    \(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)

    Jibu

    \(\dfrac{4}{15}\)

    Zoezi\(\PageIndex{24}\)

    Pata quotient:

    \(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)

    Jibu

    \(\dfrac{2}{3}\)

    Kuna njia kadhaa za kukumbuka ni hatua gani za kuchukua ili kuzidisha au kugawanya sehemu ndogo. Njia moja ni kurudia wito nje mwenyewe. Kama kufanya hivyo kila wakati kufanya zoezi, utakuwa na hatua kukariri.

    • “Ili kuzidisha sehemu ndogo, kuzidisha nambari na kuzidisha denominators.”
    • “Ili kugawanya sehemu ndogo, kuzidisha sehemu ya kwanza kwa usawa wa pili.”

    Njia nyingine ni kuweka mifano miwili katika akili:

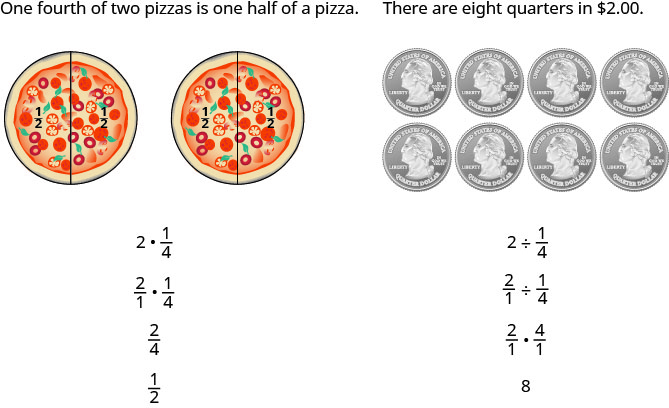
    Hii ni picha yenye nguzo mbili. Safu ya kwanza inasoma “Moja ya nne ya pizzas mbili ni nusu moja ya pizza. Chini ya hii ni pizzas mbili upande kwa upande na mstari chini katikati ya kila mmoja anayewakilisha nusu moja. Halves ni kinachoitwa “nusu moja”. Chini ya hii ni equation “mara 2 1 nne”. Chini ya hii ni equation nyingine “mbili zaidi ya mara 1 1 nne.” Chini ya hii ni sehemu ya nne na chini ya hii ni sehemu moja nusu. Safu inayofuata inasoma “kuna robo nane kwa dola mbili.” Chini ya hii ni robo nane katika safu mbili za nne. Chini ya hii ni equation ya sehemu 2 imegawanywa na moja ya nne. Chini ya hii ni equation “mbili juu ya moja kugawanywa na moja ya nne.” Chini ya hii ni mara mbili zaidi ya mara moja juu ya moja. Chini ya hii ni jibu “8".
    Kielelezo\(\PageIndex{7}\)

    Nambari au denominators ya sehemu fulani zina vyenye sehemu ndogo. Sehemu ambayo nambari au denominator ni sehemu inaitwa sehemu tata.

    SEHEMU TATA

    Sehemu ngumu ni sehemu ambayo namba au denominator ina sehemu.

    Baadhi ya mifano ya sehemu ndogo ni:

    \[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]

    Ili kurahisisha sehemu ngumu, tunakumbuka kwamba bar ya sehemu ina maana ya mgawanyiko. Kwa mfano, sehemu ngumu\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) ina maana\(\dfrac{3}{4} \div \dfrac{5}{8}\).

    Zoezi\(\PageIndex{25}\)

    Kurahisisha:\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)

    Jibu
      \(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
    Andika upya kama mgawanyiko. \(\dfrac{3}{4} \div \dfrac{5}{8}\)
    Panua sehemu ya kwanza kwa usawa wa pili. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\)
    Kuzidisha. \(\dfrac{3\cdot 8}{4\cdot 5}\)
    Angalia mambo ya kawaida. .
    Gawanya mambo ya kawaida na kurahisisha. \(\dfrac{6}{5}\)
    Zoezi\(\PageIndex{26}\)

    Kurahisisha:\(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)

    Jibu

    \(\dfrac{4}{5}\)

    Zoezi\(\PageIndex{27}\)

    Kurahisisha:\(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)

    Jibu

    \(\dfrac{11}{14}\)

    Zoezi\(\PageIndex{28}\)

    Kurahisisha:\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)

    Jibu
      \(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
    Andika upya kama mgawanyiko. \(\dfrac{x}{2} \div \dfrac{xy}{6}\)
    Panua sehemu ya kwanza kwa usawa wa pili. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\)
    Kuzidisha. \(\dfrac{x\cdot 6}{2\cdot xy}\)
    Angalia mambo ya kawaida. .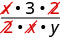
    Gawanya mambo ya kawaida na kurahisisha. \(\dfrac{3}{y}\)
    Zoezi\(\PageIndex{29}\)

    Kurahisisha:\(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)

    Jibu

    \(\dfrac{3}{4b}\)

    Zoezi\(\PageIndex{30}\)

    Kurahisisha:\(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)

    Jibu

    \(\dfrac{4}{q}\)

    Kurahisisha Maneno na Bar Fraction

    Mstari unaotenganisha nambari kutoka kwa denominator katika sehemu inaitwa bar ya sehemu. Bar ya sehemu hufanya kama ishara ya kikundi. Utaratibu wa shughuli basi inatuambia kurahisisha nambari halafu denominator. Kisha tunagawanya.

    Ili kurahisisha maneno\(\dfrac{5 - 3}{7 + 1}\), sisi kwanza kurahisisha nambari na denominator tofauti. Kisha tunagawanya.

    \[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]

    KURAHISISHA KUJIELEZA NA BAR YA SEHEMU.
    1. Kurahisisha maneno katika nambari. Kurahisisha usemi katika denominator.
    2. Kurahisisha sehemu.
    Zoezi\(\PageIndex{31}\)

    Kurahisisha:\(\dfrac{4 - 2(3)}{2^{2} + 2}\)

    Jibu

    \[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]

    Zoezi\(\PageIndex{32}\)

    Kurahisisha:\(\dfrac{6 - 3(5)}{3^{2} + 3}\)

    Jibu

    \(-\dfrac{3}{4}\)

    Zoezi\(\PageIndex{33}\)

    Kurahisisha:\(\dfrac{4 - 4(6)}{3^{2} + 3}\)

    Jibu

    \(-\dfrac{5}{3}\)

    Ishara mbaya huenda wapi sehemu? Kawaida ishara hasi iko mbele ya sehemu, lakini wakati mwingine utaona sehemu na namba hasi, au wakati mwingine na denominator hasi. Kumbuka kwamba sehemu ndogo zinawakilisha mgawanyiko. Wakati nambari na denominator zina ishara tofauti, quotient ni hasi.

    \[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]

    UWEKAJI WA ISHARA HASI KATIKA SEHEMU

    Kwa idadi yoyote chanya\(a\) na\(b\),

    \[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]

    Zoezi\(\PageIndex{34}\)

    Kurahisisha:\(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)

    Jibu

    Bar ya sehemu hufanya kama ishara ya kikundi. Hivyo kurahisisha kabisa nambari na denominator tofauti.

    \[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]

    Zoezi\(\PageIndex{35}\)

    Kurahisisha:\(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)

    Jibu

    \(4\)

    Zoezi\(\PageIndex{36}\)

    Kurahisisha:\(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)

    Jibu

    \(2\)

    Tafsiri Maneno kwa Maneno na Fractions

    Sasa kwa kuwa tumefanya kazi fulani na sehemu ndogo, tuko tayari kutafsiri misemo ambayo ingeweza kusababisha maneno na sehemu ndogo.

    Maneno ya Kiingereza quotient na uwiano mara nyingi hutumiwa kuelezea sehemu ndogo. Kumbuka kwamba “quotient” inamaanisha mgawanyiko. Quotient ya aa na b ni matokeo tunayopata kutokana\(a\) na kugawa na\(b\), au\(\dfrac{a}{b}\).

    Zoezi\(\PageIndex{37}\)

    Tafsiri maneno ya Kiingereza katika kujieleza kwa algebraic: quotient ya tofauti ya\( m\) na\(n\), na\(p\).

    Jibu

    Sisi ni kuangalia kwa quotient ya tofauti ya\(m\) na\(n\), na\(p\).. Hii ina maana tunataka kugawanya tofauti ya\(m\) na\(n\), na\(p\).

    \[\dfrac{m - n}{p}\]

    Zoezi\(\PageIndex{38}\)

    Tafsiri maneno ya Kiingereza katika kujieleza kwa algebraic: quotient ya tofauti ya\(a\) na\(b\), na\(cd\).

    Jibu

    \(\dfrac{a - b}{cd}\)

    Zoezi\(\PageIndex{39}\)

    Tafsiri maneno ya Kiingereza katika kujieleza kwa algebraic: quotient ya jumla ya\(p\) na\(q\), na\(r\).

    Jibu

    \(\dfrac{p + q}{r}\)

    Dhana muhimu

    • Sawa Fractions Mali: Kama\(a, b, c\) ni idadi ambapo\(b\neq 0, c\neq 0\), basi
      \(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) na\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\)
    • Sehemu Division: Kama\(a, b, c\) na\(d\) ni idadi ambapo\(b\neq 0, c\neq 0\) na\(d \neq 0\), kisha\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). Ili kugawanya sehemu ndogo, kuzidisha sehemu ya kwanza kwa usawa wa pili.
    • Fraction Kuzidisha: Kama\(a,b,c\) na\(d\) ni idadi ambapo\(b\neq 0, d\neq 0\), basi\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). Ili kuzidisha sehemu ndogo, kuzidisha nambari na kuzidisha denominators.
    • Uwekaji wa Hasi Ishara katika Fraction: Kwa idadi yoyote chanya\(a\) na\(b\),\(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
    • Mali ya Moja:\(\dfrac{a}{a} = 1\); Nambari yoyote, isipokuwa sifuri, imegawanywa na yenyewe ni moja.
    • Kurahisisha sehemu
      1. Andika upya nambari na denominator ili kuonyesha mambo ya kawaida. Ikiwa inahitajika, fikiria namba na denominator katika namba za kwanza kwanza.
      2. Kurahisisha kutumia sawa FRACTIONS mali kwa kugawa nje mambo ya kawaida.
      3. Panua mambo yoyote iliyobaki.
    • Kurahisisha kujieleza na Bar Fraction
      1. Kurahisisha maneno katika nambari. Kurahisisha usemi katika denominator.
      2. Kurahisisha sehemu.

    faharasa

    sehemu tata
    Sehemu ngumu ni sehemu ambayo nambari au denominator ina sehemu.
    denominator
    Denominator ni thamani kwenye sehemu ya chini ya sehemu inayoonyesha idadi ya sehemu sawa ambazo nzima imegawanywa.
    sehemu sawa
    Sehemu ndogo sawa ni sehemu ndogo ambazo zina thamani sawa.
    sehemu
    Sehemu imeandikwa\(\frac{a}{b}\), ambapo\(b\neq 0\), ni namba na b ni denominator. Sehemu inawakilisha sehemu ya nzima. Denominator b ni idadi ya sehemu sawa ambazo zote zimegawanywa, na namba aa inaonyesha sehemu ngapi zinajumuishwa.
    tarakimu
    Nambari ni thamani kwenye sehemu ya juu ya sehemu inayoonyesha sehemu ngapi za jumla zinajumuishwa.
    kurudisha nyuma
    Usawa wa\(\frac{a}{b}\) ni\(\frac{b}{a}\). Nambari na kuongezeka kwake kwa moja:\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
    sehemu kilichorahisishwa
    Sehemu inachukuliwa kuwa rahisi ikiwa hakuna mambo ya kawaida katika nambari yake na denominator.