16.7E: Mazoezi ya Sehemu ya 16.7

Last updated
Save as PDF

Page ID: 178922

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 6, bila kutumia theorem ya Stokes, kuhesabu moja kwa moja mzunguko wa$curl \, \vecs F \cdot \vecs N$ juu ya uso uliopewa na mzunguko muhimu karibu na mipaka yake, kwa kuzingatia wote ni oriented clockwise.

1. $\vecs F(x,y,z) = y^2\,\mathbf{\hat i} + z^2\,\mathbf{\hat j} + x^2\,\mathbf{\hat k}$;$S$ ni sehemu ya kwanza ya ndege$x + y + z = 1$.

2. $\vecs F(x,y,z) = z\,\mathbf{\hat i} + x\,\mathbf{\hat j} + y\,\mathbf{\hat k}$;$S$ ni hemisphere$z = (a^2 - x^2 - y^2)^{1/2}$.

Jibu: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = \pi a^2$

3. $\vecs F(x,y,z) = y^2\,\mathbf{\hat i} + 2x\,\mathbf{\hat j} + 5\,\mathbf{\hat k}$;$S$ ni hemisphere$z = (4 - x^2 - y^2)^{1/2}$.

4. $\vecs F(x,y,z) = z\,\mathbf{\hat i} + 2x\,\mathbf{\hat j} + 3y\,\mathbf{\hat k}$;$S$ ni hemisphere ya juu$z = \sqrt{9 - x^2 - y^2}$.

Jibu: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = 18 \pi$

5. $\vecs F(x,y,z) = (x + 2z)\,\mathbf{\hat i} + (y - x)\,\mathbf{\hat j} + (z - y)\,\mathbf{\hat k}$;$S$ ni kanda ya triangular yenye vertices$(3, 0, 0), \, (0, 3/2, 0),$ na$(0, 0, 3).$

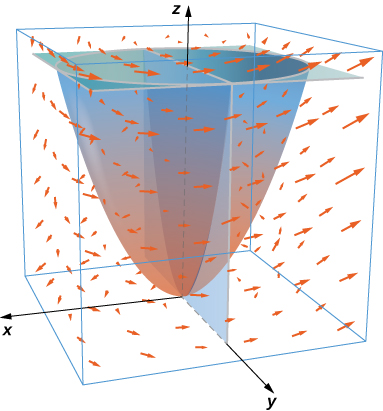
6. $\vecs F(x,y,z) = 2y\,\mathbf{\hat i} + 6z\,\mathbf{\hat j} + 3x\,\mathbf{\hat k}$;$S$ ni sehemu ya paraboloid$z = 4 - x^2 - y^2$ na ni juu$xy$ -ndege.

Jibu: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = -8 \pi$

Katika mazoezi ya 7 - 9, tumia theorem ya Stokes kutathmini$\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS$ kwa mashamba ya vector na uso.

7. $\vecs F(x,y,z) = xy\,\mathbf{\hat i} - z\,\mathbf{\hat j}$na$S$ ni uso wa mchemraba$0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$, ila kwa uso ambapo$z = 0$ na kutumia kitengo cha nje vector kawaida.

8. $\vecs F(x,y,z) = xy\,\mathbf{\hat i} + x^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}$; na$C$ ni makutano ya paraboloid$z = x^2 + y^2$ na ndege$z = y$, na kutumia vector nje ya kawaida.

Jibu: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS = 0$

9. $\vecs F(x,y,z) = 4y\,\mathbf{\hat i} + z \,\mathbf{\hat j} + 2y \,\mathbf{\hat k}$; na$C$ ni makutano ya nyanja$x^2 + y^2 + z^2 = 4$ na ndege$z = 0$, na kutumia vector nje ya kawaida.

10. Matumizi Theorem Stokes 'kutathmini$\displaystyle \int_C \big[2xy^2z \, dx + 2x^2yz \, dy + (x^2y^2 - 2z) \, dz\big],$ ambapo$C$ ni Curve iliyotolewa na$x = \cos t, \, y = \sin t, \, 0 \leq t \leq 2\pi$, traversed katika mwelekeo wa kuongeza$t.$

$Shamba la vector katika nafasi tatu za mwelekeo. Mishale ni kubwa zaidi ni kutoka ndege ya x, y. Mishale hupanda kutoka chini ya ndege ya x, y na kidogo juu yake. Wengine huwa na kupungua chini na kwa usawa. Curve ya mviringo inayotolewa katikati ya nafasi.$

Jibu: $\displaystyle \int_C \vecs F \cdot dS = 0$

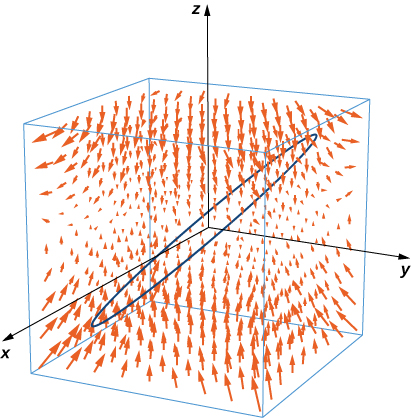
11. [T] Use a computer algebraic system (CAS) and Stokes’ theorem to approximate line integral $\displaystyle \int_C (y \, dx + z \, dy + x \, dz),$ where $C$ is the intersection of plane $x + y = 2$ and surface $x^2 + y^2 + z^2 = 2(x + y)$, traversed counterclockwise viewed from the origin.

12. [T] Use a CAS and Stokes’ theorem to approximate line integral $\displaystyle \int_C (3y\, dx + 2z \, dy - 5x \, dz),$ where $C$ is the intersection of the $xy$-plane and hemisphere $z = \sqrt{1 - x^2 - y^2}$, traversed counterclockwise viewed from the top—that is, from the positive $z$-axis toward the $xy$-plane.

Answer: $\displaystyle \int_C \vecs F \cdot dS = - 9.4248$

13. [T] Use a CAS and Stokes’ theorem to approximate line integral $\displaystyle \int_C [(1 + y) \, z \, dx + (1 + z) x \, dy + (1 + x) y \, dz],$ where $C$ is a triangle with vertices $(1,0,0), \, (0,1,0)$, and $(0,0,1)$ oriented counterclockwise.

14. Use Stokes’ theorem to evaluate $\displaystyle \iint_S curl \, \vecs F \cdot dS,$ where $\vecs F(x,y,z) = e^{xy} cos \, z\,\mathbf{\hat i} + x^2 z\,\mathbf{\hat j} + xy\,\mathbf{\hat k}$, and $S$ is half of sphere $x = \sqrt{1 - y^2 - z^2}$, oriented out toward the positive $x$-axis.

Answer: $\displaystyle \iint_S \vecs F \cdot dS = 0$

15. [T] Use a CAS and Stokes’ theorem to evaluate $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) \, dS,$ where $\vecs F(x,y,z) = x^2 y\,\mathbf{\hat i} + xy^2 \,\mathbf{\hat j} + z^3 \,\mathbf{\hat k}$ and $C$ is the curve of the intersection of plane $3x + 2y + z = 6$ and cylinder $x^2 + y^2 = 4$, oriented clockwise when viewed from above.

16. [T] Use a CAS and Stokes’ theorem to evaluate $\displaystyle \iint_S curl \, \vecs F \cdot dS,$ where $\vecs F(x,y,z) = \left( \sin(y + z) - yx^2 - \dfrac{y^3}{3}\right)\,\mathbf{\hat i} + x \, \cos (y + z) \,\mathbf{\hat j} + \cos (2y) \,\mathbf{\hat k}$ and $S$ consists of the top and the four sides but not the bottom of the cube with vertices $(\pm 1, \, \pm1, \, \pm1)$, oriented outward.

Answer: $\displaystyle \iint_S curl \, \vecs F \cdot dS = 2.6667$

17. [T] Use a CAS and Stokes’ theorem to evaluate $\displaystyle \iint_S curl \, \vecs F \cdot dS,$ where $\vecs F(x,y,z) = z^2\,\mathbf{\hat i} + 3xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}$ and $S$ is the top part of $z = 5 - x^2 - y^2$ above plane $z = 1$ and $S$ is oriented upward.

18. Use Stokes’ theorem to evaluate $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) dS,$ where $\vecs F(x,y,z) = z^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + x\,\mathbf{\hat k}$ and $S$ is a triangle with vertices $(1, 0, 0), \, (0, 1, 0)$ and $(0, 0, 1)$ with counterclockwise orientation.

Answer: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N)dS = -\dfrac{1}{6}$

19. Use Stokes’ theorem to evaluate line integral $\displaystyle \int_C (z \, dx + x \, dy + y \, dz),$ where $C$ is a triangle with vertices $(3, 0, 0), \, (0, 0, 2),$ and $(0, 6, 0)$ traversed in the given order.

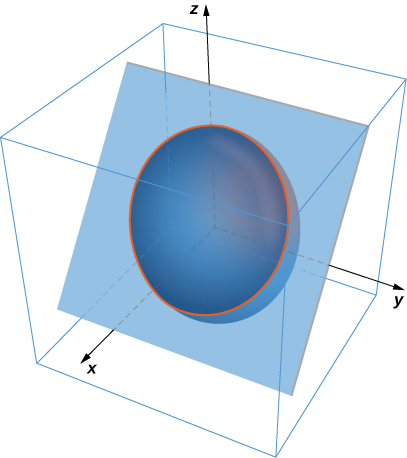
20. Use Stokes’ theorem to evaluate $\displaystyle \int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right),$ where $C$ is the curve of intersection of plane $x + z = 1$ and ellipsoid $x^2 + 2y^2 + z^2 = 1$, oriented clockwise from the origin.

$A diagram of an intersecting plane and ellipsoid in three dimensional space. There is an orange curve drawn to show the intersection.$

Jibu: $\displaystyle \int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right) = - \dfrac{\pi}{4}$

21. Matumizi Stokes 'theorem kutathmini$\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N) dS,$ wapi$\vecs F(x,y,z) = x\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + ze^{xy}\,\mathbf{\hat k}$ na$S$ ni sehemu ya uso$z = 1 - x^2 - 2y^2$ na$z \geq 0$, oriented kinyume chake.

22. Matumizi Stokes 'theorem kwa ajili ya uwanja vector$\vecs F(x,y,z) = z\,\mathbf{\hat i} + 3x\,\mathbf{\hat j} + 2z\,\mathbf{\hat k}$ ambapo$S$ ni uso$z = 1 - x^2 - 2y^2, \, z \geq 0$,$C$ ni mduara wa mipaka$x^2 + y^2 = 1$, na$S$ ni oriented katika chanya$z$ -mwelekeo.

Jibu: $\displaystyle \iint_S (curl \, \vecs F \cdot \vecs N)dS = -3\pi$

23. Matumizi Stokes 'theorem kwa ajili ya uwanja vector$\vecs F(x,y,z) = - \dfrac{3}{2} y^2\,\mathbf{\hat i} - 2 xy\,\mathbf{\hat j} + yz\,\mathbf{\hat k}$, ambapo$S$ ni kwamba sehemu ya uso wa ndege$x + y + z = 1$ zilizomo ndani ya pembetatu$C$$(1, 0, 0), \, (0, 1, 0),$ na$(0, 0, 1),$ vipeo na kupita kinyume chake kama kutazamwa kutoka juu.

24. Njia fulani iliyofungwa$C$ katika ndege$2x + 2y + z = 1$ inajulikana kwa mradi kwenye mduara wa kitengo$x^2 + y^2 = 1$ katika$xy$ -ndege. Hebu$C$ kuwa mara kwa mara na basi$\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}$. Tumia theorem Stokes 'kutathmini$\displaystyle \int_C(c \,\mathbf{\hat k} \times \vecs R) \cdot dS.$

Jibu: $\displaystyle \int_C (c \,\mathbf{\hat k} \times \vecs R) \cdot dS = 2\pi c$

25. Matumizi Stokes 'theorem na basi$C$ kuwa mipaka ya uso$z = x^2 + y^2$ na$0 \leq x \leq 2$ na$0 \leq y \leq 1$ oriented na zaidi inakabiliwa kawaida. Eleza$\vecs F(x,y,z) = \big(\sin (x^3) + xz\big) \,\mathbf{\hat i} + (x - yz)\,\mathbf{\hat j} + \cos (z^4) \,\mathbf{\hat k}$ na tathmini$\int_C \vecs F \cdot dS$.

26. Hebu$S$ kuwa hemisphere$x^2 + y^2 + z^2 = 4$ na$z \geq 0$, oriented juu. Hebu$\vecs F(x,y,z) = x^2 e^{yz}\,\mathbf{\hat i} + y^2 e^{xz} \,\mathbf{\hat j} + z^2 e^{xy}\,\mathbf{\hat k}$ kuwa uwanja wa vector. Tumia theorem Stokes 'kutathmini$\displaystyle \iint_S curl \, \vecs F \cdot dS.$

Jibu: $\displaystyle \iint_S curl \, \vecs F \cdot dS = 0$

27. Hebu$\vecs F(x,y,z) = xy\,\mathbf{\hat i} + (e^{z^2} + y)\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}$ na hebu$S$ kuwa grafu ya kazi$y = \dfrac{x^2}{9} + \dfrac{z^2}{9} - 1$ na$z \leq 0$ oriented ili vector kawaida$S$ ina chanya y sehemu. Matumizi Theorem Stokes 'kukokotoa muhimu$\displaystyle \iint_S curl \, \vecs F \cdot dS.$

28. Tumia theorem ya Stokes kutathmini$\displaystyle \oint \vecs F \cdot dS,$ wapi$\vecs F(x,y,z) = y\,\mathbf{\hat i} + z\,\mathbf{\hat j} + x\,\mathbf{\hat k}$ na$C$ ni pembetatu yenye vipeo$(0, 0, 0), \, (2, 0, 0)$ na$0,-2,2)$ inaelekezwa kinyume chake wakati unapotazamwa kutoka hapo juu.

Jibu: $\displaystyle \oint \vecs F \cdot dS = -4$

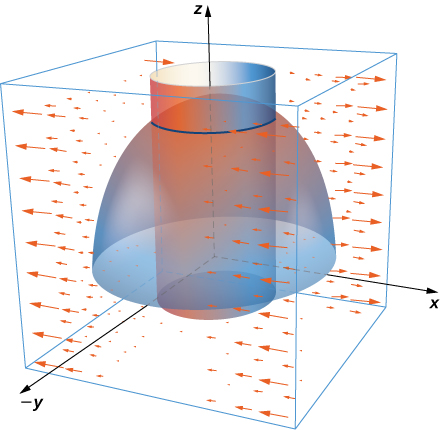
29. Matumizi ya uso muhimu katika Theorem Stokes 'kwa mahesabu ya mzunguko wa shamba$\vecs F,$$\vecs F(x,y,z) = x^2y^3 \,\mathbf{\hat i} + \,\mathbf{\hat j} + z\,\mathbf{\hat k}$ kote$C,$ ambayo ni makutano ya silinda$x^2 + y^2 = 4$ na ulimwengu$x^2 + y^2 + z^2 = 16, \, z \geq 0$, oriented kinyume chake wakati kutazamwa kutoka juu.

$Mchoro katika vipimo vitatu vya shamba la vector na makutano ya sylinder na hemisphere. Mishale ni ya usawa na ina vipengele hasi x kwa vipengele hasi y na kuwa na vipengele chanya x kwa vipengele chanya y. Curve ya makutano kati ya hemphere na silinda hutolewa kwa bluu.$

30. Tumia theorem ya Stokes 'kukokotoa$\displaystyle \iint_S curl \, \vecs F \cdot dS.$ where $\vecs F(x,y,z) = \,\mathbf{\hat i} + xy^2\,\mathbf{\hat j} + xy^2 \,\mathbf{\hat k}$ and $S$ is a part of plane $y + z = 2$ inside cylinder $x^2 + y^2 = 1$ and oriented counterclockwise.

$A diagram of a vector field in three dimensional space showing the intersection of a plane and a cylinder. The curve where the plane and cylinder intersect is drawn in blue.$

Jibu: $\displaystyle \iint_S curl \, \vecs F \cdot dS = 0$

31. Tumia theorem ya Stokes kutathmini$\displaystyle \iint_S curl \, \vecs F \cdot dS,$ wapi$\vecs F(x,y,z) = -y^2 \,\mathbf{\hat i} + x\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}$ na$S$ ni sehemu ya ndege$x + y + z = 1$ katika octant chanya na oriented kinyume chake$x \geq 0, \, y \geq 0, \, z \geq 0$.

32. Hebu$\vecs F(x,y,z) = xy\,\mathbf{\hat i} + 2z\,\mathbf{\hat j} - 2y\,\mathbf{\hat k}$ na$C$ uwe na makutano ya ndege$x + z = 5$ na silinda$x^2 + y^2 = 9$, ambayo inaelekezwa kinyume chake wakati inatazamwa kutoka juu. Compute line muhimu ya$\vecs F$ juu ya$C$ kutumia Theorem Stokes '.

Jibu: $\displaystyle \iint_S curl \, \vecs F \cdot dS = -36 \pi$

33. [T] Matumizi CAS na basi$\vecs F(x,y,z) = xy^2\,\mathbf{\hat i} + (yz - x)\,\mathbf{\hat j} + e^{yxz}\,\mathbf{\hat k}$. Matumizi Stokes 'theorem kukokotoa uso muhimu ya curl$\vecs F$ juu ya uso$S$ na mwelekeo ndani yenye mchemraba$[0,1] \times [0,1] \times [0,1]$ na upande wa kulia kukosa.

34. Hebu$S$ kuwa ellipsoid$\dfrac{x^2}{4} + \dfrac{y^2}{9} + z^2 = 1$ oriented kinyume na basi$\vecs F$ kuwa uwanja vector na kazi sehemu ambayo kuendelea sehemu derivatives.

Jibu: $\displaystyle \iint_S curl \, \vecs F \cdot \vecs N = 0$

35. Hebu$S$ kuwa sehemu ya paraboloid$z = 9 - x^2 - y^2$ na$z \geq 0$. Thibitisha Theorem Stokes 'kwa uwanja vector$\vecs F(x,y,z) = 3z\,\mathbf{\hat i} + 4x\,\mathbf{\hat j} + 2y\,\mathbf{\hat k}$.

36. [T] Matumizi CAS na Stokes 'theorem kutathmini$\displaystyle \oint \vecs F \cdot dS,$ kama$\vecs F(x,y,z) = (3z - \sin x) \,\mathbf{\hat i} + (x^2 + e^y) \,\mathbf{\hat j} + (y^3 - \cos z) \,\mathbf{\hat k}$, ambapo$C$ ni Curve iliyotolewa na$x = \cos t, \, y = \sin t, \, z = 1; \, 0 \leq t \leq 2\pi$.

Jibu: $\displaystyle \oint_C \vecs F \cdot d\vecs{r} = 0$

37. [T] Matumizi CAS na Stokes 'theorem kutathmini$\vecs F(x,y,z) = 2y\,\mathbf{\hat i} + e^z\,\mathbf{\hat j} - \arctan x \,\mathbf{\hat k}$ na$S$ kama sehemu ya paraboloid$z = 4 - x^2 - y^2$ kukatwa na$xy$ -ndege oriented kinyume.

38. [T] Matumizi CAS kutathmini$\displaystyle \iint_S curl (F) \cdot dS,$ wapi$\vecs F(x,y,z) = 2z\,\mathbf{\hat i} + 3x\,\mathbf{\hat j} + 5y\,\mathbf{\hat k}$ na$S$ ni uso parametrically na$\vecs r(r,\theta) = r \, \cos \theta \,\mathbf{\hat i} + r \, \sin \theta \,\mathbf{\hat j} + (4 - r^2) \,\mathbf{\hat k} \, (0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 3)$.

Jibu: $\displaystyle \iint_S curl (F) \cdot dS = 84.8230$

39. Hebu$S$ kuwa paraboloid$z = a (1 - x^2 - y^2)$$z \geq 0$, kwa,$a > 0$ wapi idadi halisi. Hebu$\vecs F(x,y,z) = \langle x - y, \, y + z, \, z - x \rangle$. Kwa thamani gani (s) ya$a$ (kama ipo)$\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS$ ina thamani yake ya juu?

Kwa mazoezi ya maombi 40 - 41, lengo ni kutathmini$\displaystyle A = \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS,$ wapi$\vecs F = \langle xz, \, -xz, \, xy \rangle$ na$S$ nusu ya juu ya ellipsoid$x^2 + y^2 + 8z^2 = 1$, wapi$z \geq 0$.

40. Kutathmini muhimu uso juu ya uso rahisi zaidi kupata thamani ya$A.$

Jibu: $\displaystyle A = \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS = 0$

41. Tathmini kwa$A$ kutumia mstari muhimu.

42. Kuchukua paraboloid$z = x^2 + y^2$$0 \leq z \leq 4$, kwa, na kipande kwa ndege$y = 0$. Hebu$S$ iwe uso unaoendelea$y \geq 0$, ikiwa ni pamoja na uso wa mipango katika$xz$ -ndege. Hebu$C$ kuwa sehemu ya semicircle na mstari ambayo imefungwa cap$S$ ya ndege$z = 4$ na mwelekeo kinyume chake. Hebu$\vecs F = \langle 2z + y, \, 2x + z, \, 2y + x \rangle$. Tathmini$\displaystyle \iint_S (\vecs \nabla \times \vecs F) \cdot \vecs n \, dS.$

$Mchoro wa uwanja wa vector katika nafasi tatu dimensional ambapo paraboloid na kipeo katika asili, ndege katika y=0, na ndege katika z=4 intersect. Uso uliobaki ni nusu ya paraboloidi chini ya z=4 na juu ya y=0.$

Jibu: Template:ContribOpenStaxCalc