16.6: Uso Integrals
- Page ID
- 178908
- Pata uwakilishi wa parametric wa silinda, koni, na nyanja.
- Eleza sehemu muhimu ya kazi ya thamani ya scalar juu ya uso wa parametric.
- Tumia sehemu muhimu ya kuhesabu eneo la uso uliopewa.
- Eleza maana ya uso unaoelekezwa, kutoa mfano.
- Eleza sehemu muhimu ya shamba la vector.
- Tumia integrals ya uso ili kutatua matatizo yaliyotumika.
Tumeona kwamba mstari muhimu ni muhimu juu ya njia katika ndege au katika nafasi. Hata hivyo, ikiwa tunataka kuunganisha juu ya uso (kitu cha pande mbili) badala ya njia (kitu kimoja) katika nafasi, basi tunahitaji aina mpya ya muhimu ambayo inaweza kushughulikia ushirikiano juu ya vitu katika vipimo vya juu. Tunaweza kupanua dhana ya mstari muhimu kwa uso muhimu ili kuruhusu sisi kufanya ushirikiano huu.
Uso integrals ni muhimu kwa sababu sawa kwamba line integrals ni muhimu. Wana maombi mengi ya fizikia na uhandisi, na hutuwezesha kuendeleza matoleo ya juu ya mwelekeo wa Theorem ya Msingi ya Calculus. Hasa, integrals ya uso inatuwezesha kuzalisha theorem ya Green kwa vipimo vya juu, na huonekana katika baadhi ya theorems muhimu tunayojadili katika sehemu za baadaye.
Parametric nyuso
uso muhimu ni sawa na mstari muhimu, ila ushirikiano ni kufanyika juu ya uso badala ya njia. Kwa maana hii, integrals uso kupanua juu ya utafiti wetu wa integrals line. Kama ilivyo na integrals line, kuna aina mbili za integrals uso: uso muhimu ya kazi scalar thamani na uso muhimu ya shamba vector.
Hata hivyo, kabla ya kuunganisha juu ya uso, tunahitaji kuzingatia uso yenyewe. Kumbuka kwamba kuhesabu mstari wa scalar au vector muhimu juu ya curve\(C\), sisi kwanza tunahitaji parameterize\(C\). Kwa namna hiyo hiyo, kuhesabu uso muhimu juu ya uso\(S\), tunahitaji parameterize\(S\). Hiyo ni, tunahitaji dhana ya kazi ya uso wa parameterized (au uso wa parametric), kwa njia ile ile ambayo tayari tuna dhana ya curve parameterized.
Uso wa parameterized hutolewa na maelezo ya fomu
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
Angalia kwamba parameterization hii inahusisha vigezo viwili,\(u\) na\(v\), kwa sababu uso ni mbili-dimensional, na kwa hiyo vigezo viwili vinahitajika ili kufuatilia uso. Vigezo\(u\) na\(v\) kutofautiana juu ya kanda inayoitwa kikoa cha parameter, au nafasi ya parameter - seti ya pointi katika\(uv\) -plane ambayo inaweza kubadilishwa ndani\(\vecs r\). Kila uchaguzi wa\(u\) na\(v\) katika uwanja wa parameter hutoa uhakika juu ya uso, kama kila uchaguzi wa parameter\(t\) inatoa uhakika juu ya curve parameterized. Uso mzima umeundwa kwa kufanya uchaguzi wote unaowezekana wa\(u\) na\(v\) juu ya uwanja wa parameter.
Kutokana na parameterization ya uso
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
uwanja wa parameter wa parameterization ni seti ya pointi katika\(uv\) -plane ambayo inaweza kubadilishwa ndani\(\vecs r\).
Eleza uso\(S\) parameterized na
\[\vecs{r}(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, -\infty < u < \infty, \, -\infty < v < \infty. \nonumber \]
Suluhisho
Ili kupata wazo la sura ya uso, sisi kwanza tunapanga njama fulani. Tangu parameter uwanja ni wote wa\(\mathbb{R}^2\), tunaweza kuchagua thamani yoyote kwa ajili ya u na v na njama uhakika sambamba. Ikiwa\(u = v = 0\), basi\(\vecs r(0,0) = \langle 1,0,0 \rangle\), hivyo uhakika (1, 0, 0) umeendelea\(S\). Vile vile, pointi\(\vecs r(\pi, 2) = (-1,0,2)\) na\(\vecs r \left(\dfrac{\pi}{2}, 4\right) = (0,1,4)\) ni juu\(S\).
Ingawa pointi za kupanga njama zinaweza kutupa wazo la sura ya uso, kwa kawaida tunahitaji pointi chache kabisa ili kuona sura. Kwa kuwa ni muda mwingi wa kupanga njama kadhaa au mamia ya pointi, tunatumia mkakati mwingine. Kwa taswira\(S\), sisi taswira familia mbili ya curves kwamba uongo juu\(S\). Katika familia ya kwanza ya curves sisi kushikilia\(u\) mara kwa mara; katika familia ya pili ya curves sisi kushikilia\(v\) mara kwa mara. Hii inatuwezesha kujenga “mifupa” ya uso, na hivyo kupata wazo la sura yake.
- Tuseme kwamba\(u\) ni mara kwa mara\(K\). Kisha Curve kufuatiliwa na parameterization ni\(\langle \cos K, \, \sin K, \, v \rangle \), ambayo inatoa mstari wima kwamba huenda kwa njia ya hatua\((\cos K, \sin K, v \rangle\) katika\(xy\) -ndege.
- Tuseme kwamba\(v\) ni mara kwa mara\(K\). Kisha Curve kufuatiliwa na parameterization ni\(\langle \cos u, \, \sin u, \, K \rangle \), ambayo inatoa mduara katika ndege\(z = K\) na Radius 1 na kituo cha\((0, 0, K)\).
Ikiwa\(u\) inafanyika mara kwa mara, basi tunapata mistari ya wima; ikiwa\(v\) inafanyika mara kwa mara, basi tunapata miduara ya radius 1 iliyozingatia mstari wa wima unaozunguka asili. Kwa hiyo uso uliofanywa na parameterization ni silinda\(x^2 + y^2 = 1\) (Kielelezo\(\PageIndex{1}\)).
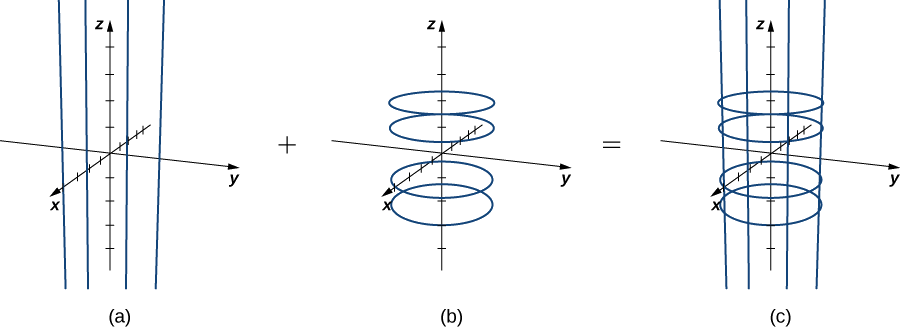
Kumbuka kwamba kama\(x = \cos u\) na\(y = \sin u\), basi\(x^2 + y^2 = 1\), hivyo pointi kutoka S kufanya kweli uongo juu ya silinda. Kinyume chake, kila hatua kwenye silinda iko kwenye mduara fulani\(\langle \cos u, \, \sin u, \, k \rangle \) kwa baadhi\(k\), na kwa hiyo kila hatua kwenye silinda iko kwenye uso wa parameterized (Kielelezo\(\PageIndex{2}\)).
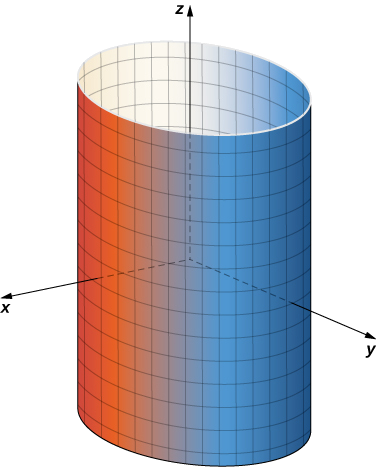
Uchambuzi
Angalia kwamba ikiwa tunabadilisha kikoa cha parameter, tunaweza kupata uso tofauti. Kwa mfano, kama sisi vikwazo uwanja kwa\(0 \leq u \leq \pi, \, -\infty < v < 6\), basi uso itakuwa nusu silinda ya urefu 6.
Eleza uso na parameterization
\[\vecs{r} (u,v) = \langle 2 \, \cos u, \, 2 \, \sin u, \, v \rangle, \, 0 \leq u \leq 2\pi, \, -\infty < v < \infty \nonumber \]
- Kidokezo
-
Kushikilia\(u\) na\(v\) mara kwa mara, na uone ni aina gani ya matokeo ya curves.
- Jibu
-
Silinda\(x^2 + y^2 = 4\)
Kutoa parameterization ya koni\(x^2 + y^2 = z^2\) iko juu au juu ya ndege\(z = -2\).
Suluhisho
Sehemu ya msalaba wa usawa wa koni kwa urefu\(z = u\) ni mduara\(x^2 + y^2 = u^2\). Kwa hiyo, hatua juu ya koni kwa urefu\(u\) ina kuratibu\((u \, \cos v, \, u \, \sin v, \, u)\) kwa angle\(v\). Kwa hiyo, parameterization ya koni ni\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle \). Kwa kuwa hatujali koni nzima, sehemu tu juu au juu ya ndege\(z = -2\), uwanja wa parameter hutolewa na\(-2 < u < \infty, \, 0 \leq v < 2\pi\) (Kielelezo\(\PageIndex{4}\)).
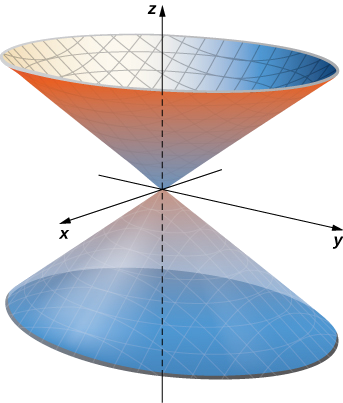
Kutoa parameterization kwa sehemu ya koni\(x^2 + y^2 = z^2\) iko katika octant ya kwanza.
- Kidokezo
-
Fikiria kikoa cha parameter kwa uso huu.
- Jibu
-
\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, 0 < u < \infty, \, 0 \leq v < \dfrac{\pi}{2}\)
Tumejadili vigezo vya nyuso mbalimbali, lakini aina mbili muhimu za nyuso zinahitaji majadiliano tofauti: nyanja na grafu za kazi mbili za kutofautiana. Ili parameterize nyanja, ni rahisi kutumia viwianishi vya spherical. Aina ya radius\(\rho\) iliyozingatia asili hutolewa na parameterization
\(\vecs r(\phi,\theta) = \langle \rho \, \cos \theta \, \sin \phi, \, \rho \, \sin \theta \, \sin \phi, \, \rho \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi.\)
Wazo la parameterization hii ni kwamba kama\(\phi\) sweeps chini kutoka chanya\(z\) -axis, mduara wa radius\(\rho \, \sin \phi\) ni chanzo chake nje kwa kuruhusu\(\theta\) kukimbia kutoka 0 hadi\(2\pi\). Ili kuona hili, hebu\(\phi\) iwe fasta. Kisha
\ [kuanza {align*} x ^ 2 + y ^ 2 &= (\ rho\,\ cos\ theta\,\ dhambi\ phi) ^2 + (\ rho\,\ dhambi\ theta\,\ dhambi\ phi) ^2\ [4pt]
&=\ rho^2\ dhambi ^ 2\ phi (\ cos ^ 2\ theta +\ dhambi ^ 2\ theta +\ dhambi ^ 2\ theta ta)\\ [4pt]
&=\ rho ^ 2\,\ dhambi ^ 2\ phi\\ [4pt]
&= (\ rho\,\ dhambi\ phi) ^2. \ mwisho {align*}\]
Hii inasababisha mduara uliotaka (Kielelezo\(\PageIndex{5}\)).
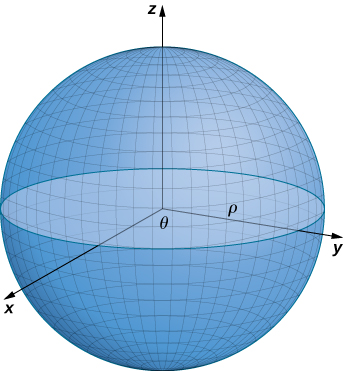
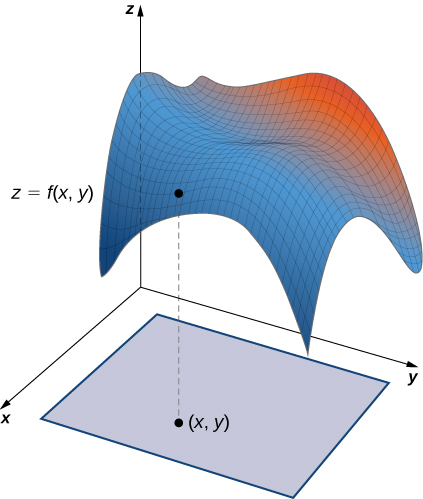
Hatimaye, kwa parameterize grafu ya kazi mbili-variable, sisi kwanza basi\(z = f(x,y)\) kuwa kazi ya vigezo mbili. Parameterization rahisi ya grafu ya\(f\) ni\(\vecs r(x,y) = \langle x,y,f(x,y) \rangle\), wapi\(x\) na\(y\) kutofautiana juu ya uwanja wa\(f\) (Kielelezo\(\PageIndex{6}\)). Kwa mfano, grafu ya\(f(x,y) = x^2 y\) inaweza parameterized na\(\vecs r(x,y) = \langle x,y,x^2y \rangle\), ambapo vigezo\(x\) na\(y\) kutofautiana juu ya uwanja wa\(f\). Ikiwa tunajali tu kuhusu kipande cha grafu ya\(f\) - sema, kipande cha grafu juu ya mstatili\([ 1,3] \times [2,5]\) - basi tunaweza kuzuia uwanja wa parameter kutoa kipande hiki cha uso:
\[\vecs r(x,y) = \langle x,y,x^2y \rangle, \, 1 \leq x \leq 3, \, 2 \leq y \leq 5. \nonumber \]
Vile vile, ikiwa\(S\) ni uso uliotolewa na equation\(x = g(y,z)\) au equation\(y = h(x,z)\), basi parameterization ya\(S\) ni\(\vecs r(y,z) = \langle g(y,z), \, y,z\rangle\) au\(\vecs r(x,z) = \langle x,h(x,z), z\rangle\), kwa mtiririko huo. Kwa mfano, grafu ya paraboloid\(2y = x^2 + z^2\) inaweza kuwa parameterized na\(\vecs r(x,y) = \left\langle x, \dfrac{x^2+z^2}{2}, z \right\rangle, \, 0 \leq x < \infty, \, 0 \leq z < \infty\). Kumbuka kwamba hatuna haja ya kutofautiana juu ya uwanja mzima wa\(y\) kwa sababu\(x\) na\(z\) ni mraba.
Hebu sasa tujalishe mawazo ya urembo na kawaida kwa uso wa parametric. Kumbuka kwamba Curve parameterization\(\vecs r(t), \, a \leq t \leq b\) ni mara kwa mara (au laini) kama\(\vecs r'(t) \neq \vecs 0\) kwa wote\(t\) katika\([a,b]\). Kwa Curve, hali hii kuhakikisha kwamba picha ya\(\vecs r\) kweli ni Curve, na si tu uhakika. Kwa mfano, fikiria parameterization ya curve\(\vecs r(t) = \langle 1,2\rangle, \, 0 \leq t \leq 5\). Picha ya parameterization hii ni uhakika tu\((1,2)\), ambayo sio safu. Kumbuka pia kwamba\(\vecs r'(t) = \vecs 0\). Ukweli kwamba derivative ni vector sifuri inaonyesha sisi si kweli kuangalia Curve.
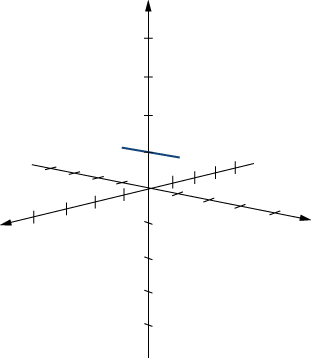
Kwa mfano, tungependa dhana ya kawaida (au urembo) kwa nyuso ili parameterization ya uso kweli haina kufuatilia nje ya uso. Ili kuhamasisha ufafanuzi wa kawaida wa parameterization ya uso, fikiria parameterization
\[\vecs r(u,v) = \langle 0, \, \cos v, \, 1 \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq \pi. \nonumber \]
Ingawa parameterization hii inaonekana kuwa parameterization ya uso, angalia kwamba picha ni kweli mstari (Kielelezo\(\PageIndex{7}\)). Tunawezaje kuepuka parameterizations kama hii? Parameterizations kwamba wala kutoa uso halisi? Kumbuka kwamba\(\vecs r_u = \langle 0,0,0 \rangle\) na\(\vecs r_v = \langle 0, -\sin v, 0\rangle\), na sambamba msalaba bidhaa ni sifuri. Analog ya hali hiyo\(\vecs r'(t) = \vecs 0\)\(\vecs r_u \times \vecs r_v\) ni kwamba sio sifuri kwa uhakika\((u,v)\) katika uwanja wa parameter, ambayo ni parameterization ya kawaida.
Parameterization\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) ni parameterization ya kawaida ikiwa\(\vecs r_u \times \vecs r_v\) sio sifuri kwa uhakika\((u,v)\) katika uwanja wa parameter.
Ikiwa parameterization\(\vec{r}\) ni ya kawaida, basi picha ya\(\vec{r}\) ni kitu mbili-dimensional, kama uso unapaswa kuwa. Katika sura hii, parameterizations\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) ni kudhani kuwa mara kwa mara.
Kumbuka kwamba Curve parameterization\(\vecs r(t), \, a \leq t \leq b\)\(\vecs r'(t)\) ni laini kama ni kuendelea na\(\vecs r'(t) \neq \vecs 0\) kwa wote\(t\) katika\([a,b]\). Kwa kawaida, parameterization ya curve ni laini ikiwa curve inayosababisha haina pembe kali. Ufafanuzi wa parameterization ya uso laini ni sawa. Kwa kawaida, parameterization ya uso ni laini ikiwa uso unaosababisha hauna pembe kali.
Parameterization\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) ya uso ni laini ikiwa vector\(\vecs r_u \times \vecs r_v\) si sifuri kwa uchaguzi wowote wa\(u\) na\(v\) katika uwanja wa parameter.
Uso unaweza pia kuwa laini ya kipande ikiwa una nyuso laini lakini pia ina maeneo ambapo derivatives ya uongozi haipo.
Ni ipi kati ya takwimu katika Kielelezo\(\PageIndex{8}\) ni laini?

Suluhisho
Upeo katika Kielelezo\(\PageIndex{8a}\) unaweza kuwa parameterized na
\[\vecs r(u,v) = \langle (2 + \cos v) \cos u, \, (2 + \cos v) \sin u, \, \sin v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v < 2\pi \nonumber \]
(tunaweza kutumia teknolojia ili kuthibitisha). Taarifa kwamba wadudu
\[\vecs r_u = \langle - (2 + \cos v)\sin u, \, (2 + \cos v) \cos u, 0 \rangle \nonumber \]
na
\[\vecs r_v = \langle -\sin v \, \cos u, \, - \sin v \, \sin u, \, \cos v \rangle \nonumber \]
zipo kwa uchaguzi wowote wa\(u\) na\(v\) katika uwanja wa parameter, na
\[ \begin{align*} \vecs r_u \times \vecs r_v &= \begin{vmatrix} \mathbf{\hat{i}}& \mathbf{\hat{j}}& \mathbf{\hat{k}} \\ -(2 + \cos v)\sin u & (2 + \cos v)\cos u & 0\\ -\sin v \, \cos u & - \sin v \, \sin u & \cos v \end{vmatrix} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [2 + \cos v) \sin u \, \cos v] \mathbf{\hat{j}} + [(2 + \cos v)\sin v \, \sin^2 u + (2 + \cos v) \sin v \, \cos^2 u]\mathbf{\hat{k}} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [(2 + \cos v) \sin u \, \cos v]\mathbf{\hat{j}} + [(2 + \cos v)\sin v ] \mathbf{\hat{k}}. \end{align*}\]
\(\mathbf{\hat{k}}\)Sehemu ya vector hii ni sifuri tu ikiwa\(v = 0\) au\(v = \pi\). Kama\(v = 0\) au\(v = \pi\), basi uchaguzi tu kwa ajili ya\(u\) kwamba kufanya\(\mathbf{\hat{j}}\) sehemu zero ni\(u = 0\) au\(u = \pi\). Lakini, uchaguzi huu wa\(u\) kufanya sifuri\(\mathbf{\hat{i}}\) sehemu. Kwa hiyo,\(\vecs r_u \times \vecs r_v\) si sifuri kwa uchaguzi wowote wa\(u\) na\(v\) katika uwanja wa parameter, na parameterization ni laini. Angalia kwamba uso unaofanana hauna pembe kali.
Katika piramidi katika Kielelezo\(\PageIndex{8b}\), ukali wa pembe huhakikisha kwamba derivatives ya uongozi haipo katika maeneo hayo. Kwa hiyo, piramidi haina parameterization laini. Hata hivyo, piramidi ina nyuso nne za laini, na hivyo uso huu ni laini.
Je, parameterization ya uso ni\(\vecs r(u,v) = \langle u^{2v}, v + 1, \, \sin u \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3\) laini?
- Kidokezo
-
Kuchunguza bidhaa msalaba\(\vecs r_u \times \vecs r_v\).
- Jibu
-
Ndio
Eneo la uso wa uso wa Parametric
Lengo letu ni kufafanua uso muhimu, na kama hatua ya kwanza tuna kuchunguza jinsi ya parameterize uso. Hatua ya pili ni kufafanua eneo la uso wa parametric. Uthibitisho unaohitajika kuendeleza ufafanuzi huu unatumiwa katika sura hii yote.
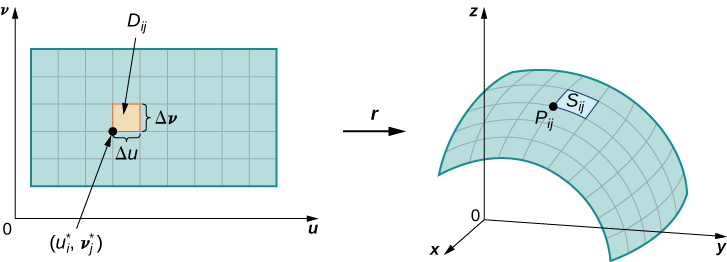
Hebu\(S\) iwe uso na parameterization\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) juu ya uwanja fulani wa parameter\(D\). Sisi kudhani hapa na katika kwamba parameterization uso\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) ni kuendelea kutofautishwa-maana, kila kazi sehemu ina kuendelea sehemu derivatives. Fikiria kwa ajili ya unyenyekevu ambao\(D\) ni mstatili (ingawa nyenzo zifuatazo zinaweza kupanuliwa ili kushughulikia vikoa vya parameter zisizo za mstatili). Gawanya mstatili\(D\) ndani ya subrectangles\(D_{ij}\) na upana usio na usawa\(\Delta u\) na urefu wa wima\(\Delta v\). Tuseme kwamba ni kati ya 1 hadi m na j ni kati ya 1 hadi n ili\(D\) imegawanywa katika rectangles mn. Mgawanyiko huu wa\(D\) ndani ya subrectangles hutoa mgawanyiko unaofanana wa uso\(S\) vipande vipande\(S_{ij}\). Chagua hatua\(P_{ij}\) katika kila kipande\(S_{ij}\). Point\(P_{ij}\) inafanana na uhakika\((u_i, v_j)\) katika uwanja wa parameter.
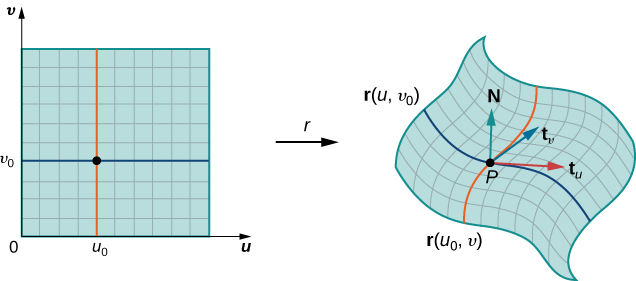
Kumbuka kwamba tunaweza kuunda gridi ya taifa na mistari ambayo ni sawa na\(u\) -axis na\(v\) -axis katika\(uv\) -ndege. Hizi mistari gridi yanahusiana na seti ya curves gridi ya taifa juu ya uso\(S\) kwamba ni parameterized na\(\vecs r(u,v)\). Bila kupoteza kwa ujumla, tunadhani kwamba\(P_{ij}\) iko kwenye kona ya curves mbili za gridi ya taifa, kama ilivyo kwenye Mchoro\(\PageIndex{9}\). Kama sisi kufikiria\(\vecs r\) kama ramani kutoka\(uv\) -ndege kwa\(\mathbb{R}^3\), curves gridi ya taifa ni mfano wa mistari gridi ya chini ya\(\vecs r\). Ili kuwa sahihi, fikiria mistari ya gridi ya taifa inayopitia hatua\((u_i, v_j)\). Mstari mmoja unatolewa na\(x = u_i, \, y = v\); nyingine hutolewa na\(x = u, \, y = v_j\). Katika mstari wa kwanza wa gridi ya taifa, sehemu ya usawa inafanyika mara kwa mara, ikitoa mstari wa wima kupitia\((u_i, v_j)\). Katika mstari wa pili wa gridi ya taifa, sehemu ya wima inafanyika mara kwa mara, ikitoa mstari usio na usawa kupitia\((u_i, v_j)\). Curves sambamba gridi ya taifa ni\(\vecs r(u_i, v)\)\((u, v_j)\) na curves hizi intersect katika hatua\(P_{ij}\).
Sasa fikiria vectors ambayo ni tangent kwa curves hizi gridi ya taifa. Kwa Curve gridi ya taifa\(\vecs r(u_i,v)\), vector tangent katika\(P_{ij}\) ni
\[\vecs t_v (P_{ij}) = \vecs r_v (u_i,v_j) = \langle x_v (u_i,v_j), \, y_v(u_i,v_j), \, z_v (u_i,v_j) \rangle. \nonumber \]
Kwa Curve gridi ya taifa\(\vecs r(u, v_j)\), vector tangent katika\(P_{ij}\) ni
\[\vecs t_u (P_{ij}) = \vecs r_u (u_i,v_j) = \langle x_u (u_i,v_j), \, y_u(u_i,v_j), \, z_u (u_i,v_j) \rangle. \nonumber \]
Ikiwa vector\(\vecs N = \vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})\) ipo na sio sifuri, basi ndege ya tangent\(P_{ij}\) iko (Kielelezo\(\PageIndex{10}\)). Kama kipande\(S_{ij}\) ni ndogo ya kutosha, basi ndege tangent katika hatua\(P_{ij}\) ni makadirio nzuri ya kipande\(S_{ij}\).
Ndege ya tangent\(P_{ij}\) ina vectors\(\vecs t_u(P_{ij})\)\(\vecs t_v(P_{ij})\) na kwa hiyo parallelogram imeenea\(\vecs t_u(P_{ij})\) na\(\vecs t_v(P_{ij})\) iko katika ndege ya tangent. Kwa kuwa mstatili wa awali katika\(uv\) -ndege inayolingana na\(S_{ij}\) ina upana\(\Delta u\) na urefu\(\Delta v\), parallelogram tunayotumia kwa takriban\(S_{ij}\) ni parallelogram iliyopigwa\(\Delta u \vecs t_u(P_{ij})\) na\(\Delta v \vecs t_v(P_{ij})\). Kwa maneno mengine, tunaongeza vectors tangent na mara kwa mara\(\Delta u\) na\(\Delta v\) kufanana na kiwango cha mgawanyiko wa awali wa rectangles katika uwanja wa parameter. Kwa hiyo, eneo la parallelogram kutumika kwa takriban eneo la\(S_{ij}\) ni
\[\Delta S_{ij} \approx ||(\Delta u \vecs t_u (P_{ij})) \times (\Delta v \vecs t_v (P_{ij})) || = ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij}) || \Delta u \,\Delta v. \nonumber \]
Tofauti uhakika\(P_{ij}\) juu ya vipande vyote\(S_{ij}\) na makadirio ya awali inaongoza kwa ufafanuzi wafuatayo wa eneo la uso wa parametric (Kielelezo\(\PageIndex{11}\)).
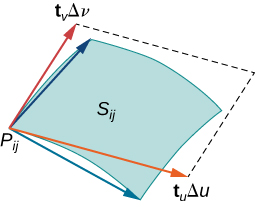
Hebu\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) na uwanja wa parameter\(D\) uwe parameterization laini ya uso\(S\). Zaidi ya hayo, kudhani kwamba\(S\) ni chanzo chake nje mara moja tu kama\((u,v)\) inatofautiana juu ya\(D\). Eneo la uso\(S\) ni
\[\iint_D ||\vecs t_u \times \vecs t_v || \,dA, \label{equation1} \]
wapi\(\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\)
na
\[\vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Tumia eneo la uso wa mviringo (eneo la “upande,” bila kujumuisha msingi) wa koni ya mviringo sahihi na urefu h na radius r.
Suluhisho
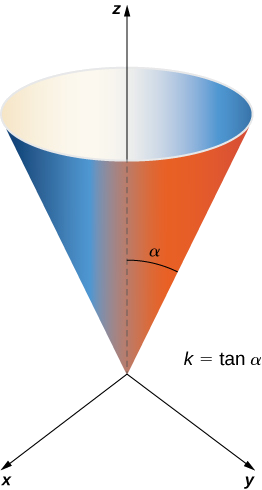
Kabla ya kuhesabu eneo la uso wa koni hii kwa kutumia Equation\ ref {equation1}, tunahitaji parameterization. Tunadhani koni hii iko\(\mathbb{R}^3\) na vertex yake katika asili (Kielelezo\(\PageIndex{12}\)). Ili kupata parameterization, hebu\(\alpha\) iwe angle ambayo imeondolewa kwa kuanzia kwenye z -axis nzuri na kuishia kwenye koni, na basi\(k = \tan \alpha\). Kwa thamani ya urefu\(v\) na\(0 \leq v \leq h\), radius ya mduara iliyoundwa na kuingiliana koni na ndege\(z = v\) ni\(kv\). Kwa hiyo, parameterization ya koni hii ni
\[\vecs s(u,v) = \langle kv \, \cos u, \, kv \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h. \nonumber \]
Wazo nyuma parameterization hii ni kwamba kwa fasta\(v\) -value, mduara swept nje kwa kuruhusu\(u\) kutofautiana ni mduara katika urefu\(v\) na Radius\(kv\). Kama\(v\) inavyoongezeka, parameterization inafuta “stack” ya miduara, na kusababisha koni inayotaka.
Kwa parameterization mkononi, tunaweza kuhesabu eneo la uso wa koni kwa kutumia Equation\ ref {equation1}. Vectors tangent ni\(\vecs t_u = \langle - kv \, \sin u, \, kv \, \cos u, \, 0 \rangle\) na\(\vecs t_v = \langle k \, \cos u, \, k \, \sin u, \, 1 \rangle\). Kwa hiyo,
\[ \begin{align*} \vecs t_u \times \vecs t_v &= \begin{vmatrix} \mathbf{\hat{i}} & \mathbf{\hat{j}} & \mathbf{\hat{k}} \\ -kv \sin u & kv \cos u & 0 \\ k \cos u & k \sin u & 1 \end{vmatrix} \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \, \sin^2 u - k^2 v \, \cos^2 u \rangle \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, - k^2 v \rangle. \end{align*}\]
Ukubwa wa vector hii ni
\[ \begin{align*} ||\langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \rangle || &= \sqrt{k^2 v^2 \cos^2 u + k^2 v^2 \sin^2 u + k^4v^2} \\[4pt] &= \sqrt{k^2v^2 + k^4v^2} \\[4pt] &= kv\sqrt{1 + k^2}. \end{align*}\]
Kwa Equation\ ref {equation1}, eneo la uso wa koni ni
\[ \begin{align*}\iint_D ||\vecs t_u \times \vecs t_v|| \, dA &= \int_0^h \int_0^{2\pi} kv \sqrt{1 + k^2} \,du\, dv \\[4pt] &= 2\pi k \sqrt{1 + k^2} \int_0^h v \,dv \\[4pt] &= 2 \pi k \sqrt{1 + k^2} \left[\dfrac{v^2}{2}\right]_0^h \\[4pt] \\[4pt] &= \pi k h^2 \sqrt{1 + k^2}. \end{align*}\]
Tangu\(k = \tan \alpha = r/h\),
\[ \begin{align*} \pi k h^2 \sqrt{1 + k^2} &= \pi \dfrac{r}{h}h^2 \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] &= \pi r h \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] \\[4pt] &= \pi r \sqrt{h^2 + h^2 \left(\dfrac{r^2}{h^2}\right) } \\[4pt] &= \pi r \sqrt{h^2 + r^2}. \end{align*}\]
Kwa hiyo, eneo la uso wa koni ni\(\pi r \sqrt{h^2 + r^2}\).
UchambuziEneo la uso wa koni ya mviringo sahihi\(r\) na radius na urefu\(h\) hutolewa kama\(\pi r^2 + \pi r \sqrt{h^2 + r^2}\). Sababu ya hii ni kwamba msingi wa mviringo umejumuishwa kama sehemu ya koni, na kwa hiyo eneo la msingi\(\pi r^2\) linaongezwa kwenye eneo la uso la mviringo\(\pi r \sqrt{h^2 + r^2}\) ambalo tumepata.
Pata eneo la uso wa uso na parameterization\(\vecs r(u,v) = \langle u + v, \, u^2, \, 2v \rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 2\).
- Kidokezo
-
Tumia Equation\ ref {equation1}.
- Jibu
-
\(\≈ 43.02\)
Onyesha kwamba eneo la uso wa nyanja\(x^2 + y^2 + z^2 = r^2\) ni\(4 \pi r^2\).
Suluhisho
Sifa ina parameterization
\(r \, \cos \theta \, \sin \phi, \, r \, \sin \theta \, \sin \phi, \, r \, \cos \phi \rangle, \, 0 \leq \theta < 2\pi, \, 0 \leq \phi \leq \pi.\)
Vectors tangent ni
\(\vecs t_{\theta} = \langle -r \, \sin \theta \, \sin \phi, \, r \, \cos \theta \, \sin \phi, \, 0 \rangle\)
na
\(\vecs t_{\phi} = \langle r \, \cos \theta \, \cos \phi, \, r \, \sin \theta \, \cos \phi, \, -r \, \sin \phi \rangle.\)
Kwa hiyo,
\[ \begin{align*}\vecs t_{\phi} \times \vecs t_{\theta} &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin^2 \theta \, \sin \phi \, \cos \phi + r^2 \cos^2 \theta \, \sin \phi \, \cos \phi \rangle \\[4pt] &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin \phi \, \cos \phi \rangle. \end{align*}\]
Sasa,
\[ \begin{align*}||\vecs t_{\phi} \times \vecs t_{\theta} || &= \sqrt{r^4\sin^4\phi \, \cos^2 \theta + r^4 \sin^4 \phi \, \sin^2 \theta + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= \sqrt{r^4 \sin^4 \phi + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= r^2 \sqrt{\sin^2 \phi} \\[4pt] &= r \, \sin \phi.\end{align*}\]
Kumbuka kwamba\(\sin \phi \geq 0\) kwenye uwanja wa parameter kwa sababu\(0 \leq \phi < \pi\), na hii inathibitisha equation\(\sqrt{\sin^2 \phi} = \sin \phi\). Eneo la uso wa nyanja ni
\[\int_0^{2\pi} \int_0^{\pi} r^2 \sin \phi \, d\phi \,d\theta = r^2 \int_0^{2\pi} 2 \, d\theta = 4\pi r^2. \nonumber \]
Tumepata formula inayojulikana kwa eneo la uso wa nyanja kwa kutumia integrals ya uso.
Onyesha kwamba eneo la uso wa silinda\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\) ni\(2\pi rh\). Kumbuka kwamba silinda hii haijumuishi miduara ya juu na ya chini.
- Kidokezo
-
Tumia parameterization ya kawaida ya silinda na ufuate mfano uliopita.
- Jibu
-
Kwa parameterization ya kiwango cha silinda, Equation\ ref {equation1} inaonyesha kwamba eneo la uso ni\(2 \pi rh\).
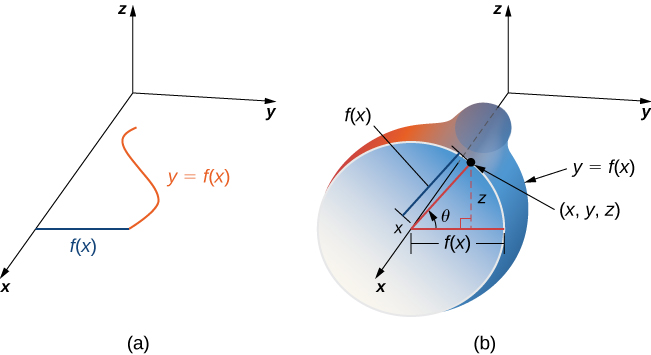
Mbali na nyuso za parameterizing zinazotolewa na equations au maumbo ya kijiometri ya kawaida kama vile mbegu na nyanja, tunaweza pia parameterize nyuso za mapinduzi. Kwa hiyo, tunaweza kuhesabu eneo la uso wa mapinduzi kwa kutumia mbinu sawa. Hebu\(y = f(x) \geq 0\) kuwa chanya moja-variable kazi kwenye uwanja\(a \leq x \leq b\) na basi\(S\) kuwa uso kupatikana kwa kupokezana\(f\) kuhusu\(x\) -axis (Kielelezo\(\PageIndex{13}\)). Hebu\(\theta\) iwe angle ya mzunguko. Kisha,\(S\) inaweza kuwa parameterized na vigezo\(x\) na\(\theta\) kwa
\[\vecs r(x, \theta) = \langle x, f(x) \, \cos \theta, \, f(x) \sin \theta \rangle, \, a \leq x \leq b, \, 0 \leq x \leq 2\pi. \nonumber \]
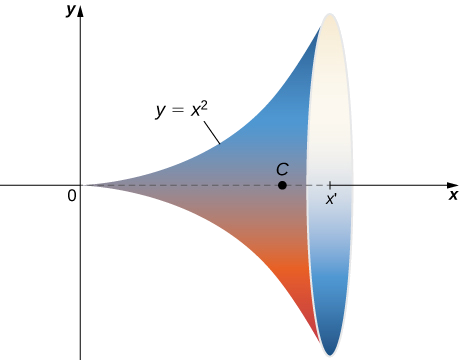
Pata eneo la uso wa mapinduzi yaliyopatikana kwa kupokezana\(y = x^2, \, 0 \leq x \leq b\) kuhusu x -axis (Kielelezo\(\PageIndex{14}\)).
Suluhisho
Uso huu una parameterization\(\vecs r(x, \theta) = \langle x, \, x^2 \cos \theta, \, x^2 \sin \theta \rangle, \, 0 \leq x \leq b, \, 0 \leq x < 2\pi.\)
Vectors tangent ni\( \vecs t_x = \langle 1, \, 2x \, \cos \theta, \, 2x \, \sin \theta \rangle\) na\(\vecs t_{\theta} = \langle 0, \, -x^2 \sin \theta, \, -x^2 \cos \theta \rangle\).
Kwa hiyo,
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \langle 2x^3 \cos^2 \theta + 2x^3 \sin^2 \theta, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \\[4pt] &= \langle 2x^3, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \end{align*}\]
na
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \sqrt{4x^6 + x^4\cos^2 \theta + x^4 \sin^2 \theta} \\[4pt] &= \sqrt{4x^6 + x^4} \\[4pt] &= x^2 \sqrt{4x^2 + 1} \end{align*}\]
Eneo la uso wa mapinduzi ni
\ [kuanza {align*}\ int_0 ^ b\ int_0^ {2\ pi} x ^ 2\ sqrt {4x^2 + 1}\, d\ theta\, dx &= 2\ pi\ int_0 ^ b x ^ 2\ sqrt {4x^2 + 1}\, dx\\ [4pt]
&= 2\ pi\ kushoto [\ dfrac {1} {64}\ kushoto (2\ sqrt {4x^2 + 1} (8x ^ 3 + x)\,\ sinh^ {-1} (2x)\ haki)\ haki] _0 ^ b\\ [4pt]
&= 2\ pi\ kushoto [\ dfrac {1} {64}\ kushoto (2 \ sqrt {4b ^ 2 + 1} (8b ^ 3 + b)\,\ sinh^ {-1} (2b)\ haki)\ haki]. \ mwisho {align*}\]
Tumia Equation\ ref {equation1} ili upate eneo la uso wa mapinduzi lililopatikana kwa kupokezana curve\(y = \sin x, \, 0 \leq x \leq \pi\) kuhusu\(x\) -axis.
- Kidokezo
-
Tumia parameterization ya nyuso za mapinduzi iliyotolewa kabla ya Mfano\(\PageIndex{7}\).
- Jibu
-
\(2\pi (\sqrt{2} + \sinh^{-1} (1))\)
Surface Integral ya Kazi Scalar-Thamani
Sasa kwa kuwa tunaweza parameterize nyuso na tunaweza kuhesabu maeneo yao ya uso, tunaweza kufafanua integrals uso. Kwanza, hebu tuangalie sehemu muhimu ya kazi ya thamani ya scalar. Kwa kawaida, sehemu muhimu ya kazi ya thamani ya scalar ni analog ya mstari wa scalar muhimu katika mwelekeo mmoja wa juu. Uwanja wa ushirikiano wa mstari wa mstari wa scalar ni safu ya parameterized (kitu kimoja); uwanja wa ushirikiano wa uso wa scalar muhimu ni uso wa parameterized (kitu mbili-dimensional). Kwa hiyo, ufafanuzi wa uso muhimu hufuata ufafanuzi wa mstari unaofaa kwa karibu sana. Kwa integrals scalar line, sisi kung'olewa Curve uwanja katika vipande vidogo, alichagua hatua katika kila kipande, computed kazi katika hatua hiyo, na kuchukua kikomo ya sambamba Riemann jumla. Kwa integrals uso scalar, sisi kukata mkoa wa kikoa (tena curve) katika vipande vidogo na kuendelea kwa mtindo huo.
Hebu\(S\) iwe uso wa laini na parameterization\(\vecs{r}(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle \) na kikoa cha parameter\(D\) na basi\(f(x,y,z)\) iwe kazi na kikoa kilicho na\(S\). Kwa sasa, kudhani uwanja wa parameter\(D\) ni mstatili, lakini tunaweza kupanua mantiki ya msingi ya jinsi tunavyoendelea kwenye uwanja wowote wa parameter (uchaguzi wa mstatili ni tu kufanya notation zaidi kusimamiwa). Gawanya mstatili\(D\) ndani ya subrectangles\(D_{ij}\) na upana usio na usawa\(\Delta u\) na urefu wa wima\(\Delta v\). Tuseme kwamba\(i\) ni kati\(1\) ya hadi\(m\) na\(D\) ni\(j\) kati\(1\) ya hadi\(n\) hivyo kwamba imegawanywa katika\(mn\) rectangles. Mgawanyiko huu wa\(D\) ndani ya subrectangles hutoa mgawanyiko unaofanana wa\(S\) vipande vipande\(S_{ij}\). Chagua hatua\(P_{ij}\) katika kila kipande\(S_{ij}\) kutathmini\(P_{ij}\) saa\(f\), na kuzidisha\(S_{ij}\) kwa eneo kuunda jumla Riemann
\[\sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \, \Delta S_{ij}. \nonumber \]
Ili kufafanua sehemu muhimu ya kazi ya thamani ya scalar, tunaruhusu maeneo ya vipande vya\(S\) kupungua hadi sifuri kwa kuchukua kikomo.
uso muhimu ya scalar thamani functi\(f\) juu ya uso piecewise laini\(S\) ni
\[\iint_S f(x,y,z) dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}. \nonumber \]
Tena, angalia kufanana kati ya ufafanuzi huu na ufafanuzi wa mstari wa scalar muhimu. Katika ufafanuzi wa mstari muhimu sisi kukata Curve vipande vipande, kutathmini kazi katika hatua katika kila kipande, na kuruhusu urefu wa vipande shrink kwa sifuri kwa kuchukua kikomo cha sambamba Riemann jumla. Katika ufafanuzi wa uso muhimu, sisi kukata uso katika vipande vipande, kutathmini kazi katika hatua katika kila kipande, na kuruhusu eneo la vipande shrink kwa sifuri kwa kuchukua kikomo cha sambamba Riemann jumla. Hivyo, muhimu ya uso ni sawa na mstari muhimu lakini kwa mwelekeo mmoja wa juu.
Ufafanuzi wa mstari wa scalar muhimu unaweza kupanuliwa kwa vikoa vya parameter ambavyo si mstatili kwa kutumia mantiki hiyo iliyotumiwa mapema. Wazo la msingi ni kukata kikoa cha parameter katika vipande vidogo, chagua hatua ya sampuli katika kila kipande, na kadhalika. Sura halisi ya kila kipande katika uwanja wa sampuli inakuwa haina maana kama maeneo ya vipande hupungua hadi sifuri.
Scalar uso integrals ni vigumu kukokotoa kutoka ufafanuzi, kama scalar line integrals ni. Kuendeleza njia ambayo inafanya integrals uso rahisi compute, sisi takriban maeneo ya uso\(\Delta S_{ij}\) na vipande vidogo vya ndege tangent, kama tulivyofanya katika kifungu cha awali. Kumbuka ufafanuzi wa wadudu\(\vecs t_u\) na\(\vecs t_v\):
\[\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\, \text{and} \, \vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Kutoka kwa nyenzo ambazo tayari tumejifunza, tunajua hilo
\[\Delta S_{ij} \approx ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})|| \,\Delta u \,\Delta v. \nonumber \]
Kwa hiyo,
\[\iint_S f(x,y,z) \,dS \approx \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij})|| \vecs t_u(P_{ij}) \times \vecs t_v(P_{ij}) ||\,\Delta u \,\Delta v. \nonumber \]
Makadirio hii inakuwa kiholela karibu na\(\displaystyle \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}\) kama sisi kuongeza idadi ya vipande\(S_{ij}\) kwa kuruhusu\(m\) na\(n\) kwenda infinity. Kwa hiyo, tuna equation zifuatazo kuhesabu integrals uso scalar:
\[\iint_S f(x,y,z)\,dS = \iint_D f(\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA. \label{scalar surface integrals} \]
Equation\ ref {scalar uso integrals} inaruhusu sisi mahesabu ya uso muhimu kwa kubadilisha kuwa muhimu mara mbili. Equation hii kwa integrals uso ni sawa na equation kwa integrals line:
\[\iint_C f(x,y,z)\,ds = \int_a^b f(\vecs r(t))||\vecs r'(t)||\,dt. \nonumber \]
Katika kesi hii, vector\(\vecs t_u \times \vecs t_v\) ni perpendicular kwa uso, wakati vector\(\vecs r'(t)\) ni tangent kwa curve.
Mahesabu ya uso muhimu
\[\iint_S 5 \, dS, \nonumber \]
\(S\)wapi uso na parameterization\(\vecs r(u,v) = \langle u, \, u^2, \, v \rangle\) kwa\(0 \leq u \leq 2\) na\(0 \leq v \leq u\).
Suluhisho
Angalia kwamba uwanja huu wa parameter\(D\) ni pembetatu, na kwa hiyo uwanja wa parameter sio mstatili. Hii si suala ingawa, kwa sababu Equation\ ref {scalar uso integrals} haina kuweka vikwazo yoyote juu ya sura ya kikoa parameter.
Kutumia Equation\ ref {scalar uso integrals} kwa mahesabu ya uso muhimu, sisi kwanza kupata wadudu\(\vecs t_u\) na\(\vecs t_v\). Kumbuka kuwa\(\vecs t_u = \langle 1, 2u, 0 \rangle\) na\(\vecs t_v = \langle 0,0,1 \rangle\). Kwa hiyo,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \nonumber \\ 1 & 2u & 0 \nonumber \\ 0 & 0 & 1 \end{vmatrix} = \langle 2u, \, -1, \, 0 \rangle\ \nonumber \]
na
\[||\vecs t_u \times \vecs t_v|| = \sqrt{1 + 4u^2}. \nonumber \]
By Equation\ ref {scalar uso integrals},
\ [kuanza {align*}\ iInt_s 5\, dS &= 5\ iInt_d\ sqrt {1 + 4u ^ 2}\, da\\
&= 5\ int_0 ^ 2\ int_0 ^ u\ sqrt {1 + 4u ^ 2}\, dv\, du = 5\ int_0 ^ 2 u\ sqrt {1 + 4u ^ 2}\, du\\
&= 5\ kushoto [\ dfrac {(1+4u ^ 2) ^ {3/2}} {3}\ haki] _0 ^ 2\\
&=\ dfrac {5 (17^ {3/2} -1)} {3}\ takriban 115. 15. \ mwisho {align*}\]
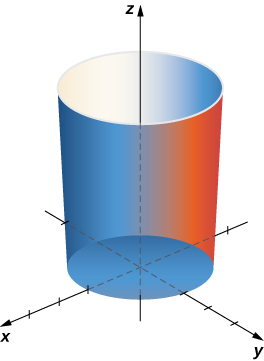
Mahesabu ya uso muhimu\[\iint_S (x + y^2) \, dS, \nonumber \] ambapo\(S\) ni silinda\(x^2 + y^2 = 4, \, 0 \leq z \leq 3\) (Kielelezo\(\PageIndex{15}\)).
Suluhisho
Ili kuhesabu muhimu ya uso, sisi kwanza tunahitaji parameterization ya silinda. parameterization ni\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, 0 \leq u \leq 2\pi, \, 0 \leq v \leq 3.\)
Vectors tangent ni\(\vecs t_u = \langle \sin u, \, \cos u, \, 0 \rangle\) na\(\vecs t_v = \langle 0,0,1 \rangle\). Kisha,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ -\sin u & \cos u & 0 \\ 0 & 0 & 1 \end{vmatrix} = \langle \cos u, \, \sin u, \, 0 \rangle \nonumber \]
na\(||\vecs t_u \times \vecs t_v || = \sqrt{\cos^2 u + \sin^2 u} = 1\). By Equation\ ref {scalar uso integrals},
\ [kuanza {align*}\ iInt_s f (x, y, z) ds &=\ iInt_d f (\ vecs r (u, v)) ||\ vecs t_u\ mara\ vecs t_v||\, da\\
&=\ int_0 ^\ int_0^ {2\ pi} (\ cos u +\ sin^2 u)\, du\, dv\\
&=\ int_0 ^ 3\ kushoto [\ dhambi u +\ dfrac {u} {2} -\ dfrac {\ dhambi (2u)} {4}\ haki] _0^ {2\ pi}\, dv\\
&= \ int_0 ^ 3\ pi\, dv = 3\ pi. \ mwisho {align*}\]
Tumia\[\iint_S (x^2 - z) \,dS, \nonumber \]\(S\) wapi uso na parameterization\(\vecs r(u,v) = \langle v, \, u^2 + v^2, \, 1 \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3.\)
- Kidokezo
-
Matumizi Equation\ ref {scalar uso integrals}.
- Jibu
-
24
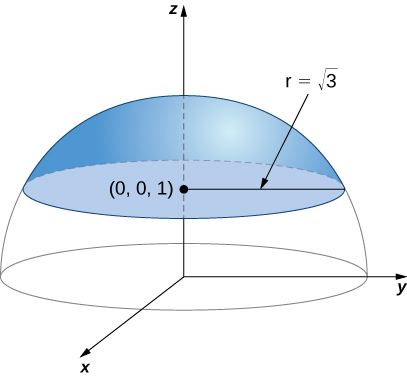
Mahesabu ya uso muhimu\[\iint_S f(x,y,z)\,dS, \nonumber \] ambapo\(f(x,y,z) = z^2\) na\(S\) ni uso ambayo ina kipande cha nyanja\(x^2 + y^2 + z^2 = 4\) ambayo iko juu au juu ya ndege\(z = 1\) na disk kwamba ni iliyoambatanishwa na makutano ndege\(z = 1\) na nyanja fulani (Kielelezo\(\PageIndex{16}\)).
Suluhisho
Angalia kwamba\(S\) si laini lakini ni kipande laini;\(S\) inaweza kuandikwa kama muungano wa msingi wake\(S_1\) na juu yake spherical\(S_2\), na wote wawili\(S_1\) na\(S_2\) ni laini. Kwa hiyo, kwa mahesabu
\[\iint_S z^2 dS, \nonumber \]
tunaandika hii muhimu kama
\[\iint_{S_1} z^2 \,dS + \iint_{S_2} z^2 \,dS \nonumber \]
na sisi mahesabu integrals
\[\iint_{S_1} z^2 \,dS \nonumber \]
na
\[\iint_{S_2}Z^2 \,dS. \nonumber \]
Kwanza, sisi mahesabu\(\displaystyle \iint_{S_1} z^2 \,dS.\) Kuhesabu muhimu hii tunahitaji parameterization ya\(S_1\). Uso huu ni disk katika ndege\(z = 1\) unaozingatia\((0,0,1)\). Ili parameterize disk hii, tunahitaji kujua radius yake. Tangu disk ni sumu ambapo ndege\(z = 1\) intersects nyanja\(x^2 + y^2 + z^2 = 4\), tunaweza mbadala\(z = 1\) katika equation\(x^2 + y^2 + z^2 = 4\):
\[x^2 + y^2 + 1 = 4 \Rightarrow x^2 + y^2 = 3. \nonumber \]
Kwa hiyo, radius ya disk ni\(\sqrt{3}\) na parameterization ya\(S_1\) ni\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, 1 \rangle, \, 0 \leq u \leq \sqrt{3}, \, 0 \leq v \leq 2\pi\). Vectors tangent ni\(\vecs t_u = \langle \cos v, \, \sin v, \, 0 \rangle \) na\(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, \, 0 \rangle\), na hivyo
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \cos v & \sin v & 0 \\ -u\sin v & u\cos v& 0 \end{vmatrix} = \langle 0, \, 0, u \, \cos^2 v + u \, \sin^2 v \rangle = \langle 0, 0, u \rangle. \nonumber \]
Ukubwa wa vector hii ni\(u\). Kwa hiyo,
\ [kuanza {align*}\ iint_ {S_1} z ^ 2\, dS &=\ int_0^ {\ sqrt {3}}\ int_0^ {2\ pi} f (r (u, v)) ||t_u\ mara t_v||\, dv\\, du\\
&=\ int_0^ {\ sqrt {3}}\ _0^ {2\ pi} u\, dv\, du\\
&= 2\ pi\ int_0^ {\ sqrt {3}} u\, du\\
&= 2\ pi\ sqrt {3}. \ mwisho {align*}\]
Sasa tunahesabu
\[\iint_{S_2} \,dS. \nonumber \]
Ili kuhesabu hii muhimu, tunahitaji parameterization ya\(S_2\). Parameterization ya nyanja kamili\(x^2 + y^2 + z^2 = 4\) ni
\[\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi. \nonumber \]
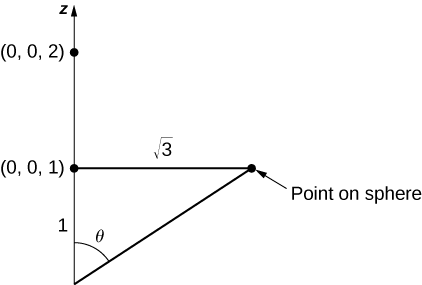
Kwa kuwa sisi ni tu kuchukua kipande cha nyanja juu ya au juu ya ndege\(z = 1\), tuna kuzuia uwanja wa\(\phi\). Kuona jinsi mbali angle hii inafuta, angalia kwamba angle inaweza kuwa iko katika pembetatu sahihi, kama inavyoonekana kwenye Mchoro\(\PageIndex{17}\) (\(\sqrt{3}\)inatokana na ukweli kwamba msingi wa\(S\) ni disk na radius\(\sqrt{3}\)). Kwa hiyo, tangent ya\(\phi\) ni\(\sqrt{3}\), ambayo ina maana kwamba\(\phi\) ni\(\pi / 6\). Sasa tuna parameterization ya\(S_2\):
\(\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi / 3.\)
Vectors tangent ni\(\vecs t_{\phi} = \langle 2 \, \cos \theta \, \cos \phi, \, 2 \, \sin \theta \,\cos \phi, \, -2 \, \sin \phi \rangle\) na\(\vecs t_{\theta} = \langle - 2 \sin \theta \sin \phi, \, u\cos \theta \sin \phi, \, 0 \rangle\), na hivyo
\ [kuanza {align*}\ vecs t_ {\ phi}\ mara\ vecs t_ {\ theta} &=\ kuanza {vmatrix}\ matriki {\ kofia i} &\ hatbf {\ kofia j} &\ hatbf {\ kofia k}\ nonumber\\ 2\ cos\ cos\ cos\ cos\\ phi & 2\ dhambi\ theta\ cos\ phi & -2\ dhambi\ phi\ -2\ dhambi\ theta\ dhambi\ phi & 2\ cos\ theta\ dhambi\ phi & 0\ mwisho {vmatrix}\\ [4 pt]
&=\ langle 4\,\ cos\ theta\,\ dhambi ^ 2\ phi,\, 4\,\ dhambi\ theta\,\ dhambi ^ 2\ phi,\, 4\,\ cos ^ 2\ theta\,\ cos\ phi\,\ dhambi\ phi + 4\,\ dhambi ^ 2\ theta\,\ cos\ phi\,\ dhambi\ phi\ rangle\\ [4 pt]
&=\ langle 4\,\ cos\ theta\,\ dhambi ^ 2\ phi,\, 4\,\ dhambi\ theta\,\ dhambi ^ 2\ phi,\, 4\,\ cos\ phi\,\ sin\ phi\ rangle. \ mwisho {align*}\]
Ukubwa wa vector hii ni
\ [kuanza {align*}\ vecs t_ {\ phi}\ mara\ vecs t_ {\ theta} &=\ sqrt {16\,\ cos ^ 2\ theta\,\ dhambi ^ 4\ phi + 16\,\ dhambi ^ 2\ theta\,\ dhambi ^ 4\ phi + 16\,\ cos ^ 2\ phi\,\ dhambi ^ 2\ phi i}\\ [4 pt]
&= 4\ sqrt {\ sin^4\ phi +\ cos ^ 2\ phi\,\ dhambi ^ 2\ phi}. \ mwisho {align*}\]
Kwa hiyo,
\ [kuanza {align*}\ iint_ {S_2} z\, D &=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} f (\ vecs r (\ phi,\ theta)) ||\ vecs t_ {\ phi}\ mara\ vecs t_ {\ theta} ||\ d\ theta\, d\ phi\\
&=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} 16\,\ cos^2\ phi\ sqrt {\ dhambi ^ 4\ phi +\ cos ^ 2\ phi\,\ dhambi ^ 2\ phi}\, d\ theta\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos ^ 2\ phi\ sqrt {\ dhambi ^ 4\ phi +\ cos ^ 2\ phi\,\ dhambi ^ 2\ phi}\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\,\ dhambi\ phi\ sqrt {\ pi/6}\ cos ^ 2\ phi\,\ dhambi\ phi\ sqrt {\ pi/6}\ dhambi ^ 2\ phi +\ cos ^ 2\ phi}\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos ^ 2\ phi\,\ dhambi\ phi\\, d\ phi\\
& = 32\ pi\ kushoto [-\ dfrac {\ cos^3\ phi} {3}\ haki] _0^ {\ pi/6}\\
&= 32\ pi\ kushoto [\ dfrac {1} {3} -\ dfrac {\ sqrt {3} {\ sqrt {3} {4\ sqrt {8}\ haki] =\ dfrac {32\ pi} {3} - 4\ sqrt {3}. \ mwisho {align*}\]
Tangu
\[\iint_S z^2 \,dS = \iint_{S_1}z^2 \,dS + \iint_{S_2}z^2 \,dS, \nonumber \]
tuna
\[\iint_S z^2 \,dS = (2\pi - 4) \sqrt{3} + \dfrac{32\pi}{3}. \nonumber \]
Uchambuzi
Katika mfano huu sisi kuvunja uso muhimu juu ya uso piecewise katika kuongeza ya integrals uso juu ya subsurfaces laini. Kulikuwa na subsurfaces mbili tu laini katika mfano huu, lakini mbinu hii inaendelea kwa subsurfaces nyingi laini.
Mahesabu line muhimu\(\displaystyle \iint_S (x - y) \, dS,\) ambapo\(S\) ni silinda\(x^2 + y^2 = 1, \, 0 \leq z \leq 2\), ikiwa ni pamoja na juu ya mviringo na chini.
- Kidokezo
-
Kuvunja muhimu katika integrals tatu tofauti ya uso.
- Jibu
-
0
Scalar uso integrals na maombi kadhaa halisi ya dunia. Kumbuka kwamba integrals mstari scalar inaweza kutumika kukokotoa wingi wa waya kutokana na wiani kazi yake. Kwa mtindo sawa, tunaweza kutumia integrals uso scalar kukokotoa wingi wa karatasi kutokana na wiani kazi yake. Kama karatasi nyembamba ya chuma ina sura ya uso\(S\) na wiani wa karatasi katika hatua\((x,y,z)\) ni\(\rho(x,y,z)\) basi wingi\(m\) wa karatasi ni
\[\displaystyle m = \iint_S \rho (x,y,z) \,dS. \label{mass} \]
Karatasi ya gorofa ya chuma ina sura ya uso\(z = 1 + x + 2y\) iliyo juu ya mstatili\(0 \leq x \leq 4\) na\(0 \leq y \leq 2\). Ikiwa wiani wa karatasi hutolewa na\(\rho (x,y,z) = x^2 yz\), ni kiasi gani cha karatasi?
Suluhisho
Hebu\(S\) iwe uso unaoelezea karatasi. Kisha, wingi wa karatasi hutolewa na\(\displaystyle m = \iint_S x^2 yx \, dS.\) Ili kukokotoa hii muhimu ya uso, sisi kwanza tunahitaji parameterization ya\(S\). Tangu\(S\) hutolewa na kazi\(f(x,y) = 1 + x + 2y\), parameterization ya\(S\) ni\(\vecs r(x,y) = \langle x, \, y, \, 1 + x + 2y \rangle, \, 0 \leq x \leq 4, \, 0 \leq y \leq 2\).
Vectors tangent ni\(\vecs t_x = \langle 1,0,1 \rangle\) na\(\vecs t_y = \langle 1,0,2 \rangle\). Kwa hiyo,\(\vecs t_x + \vecs t_y = \langle -1,-2,1 \rangle\) na\(||\vecs t_x \times \vecs t_y|| = \sqrt{6}\).
Kwa ufafanuzi wa mstari muhimu (Sehemu ya 16.2),\ [kuanza {align*} m &=\ Iint_s x ^ 2 yz\, ds\\ [4pt]
&=\ sqrt {6}\ int_0 ^ 4\ int_0 ^ 2 x ^ 2 y (1 + x + 2y)\, dy\\, dx\\ [4pt]
&=\ sqrt {6}\ int_0 ^ 4\ dfrac {22x^2} {3} + 2x^3\, dx\\ [4pt]
&=\ dfrac {2560\ sqrt { 6}} {9}\ takriban 696.74. \ mwisho {align*}\]
Kipande cha chuma kina umbo linalotokana na paraboloidi\(z = x^2 + y^2, \, 0 \leq z \leq 4,\) na wiani wa chuma hutolewa na\(\rho (x,y,z) = z + 1\). Pata wingi wa kipande cha chuma.
- Kidokezo
-
Masi ya karatasi hutolewa na Equation\ ref {mass}. Parameterization muhimu ya paraboloid ilitolewa katika mfano uliopita.
- Jibu
-
\(38.401 \pi \approx 120.640\)
Mwelekeo wa Uso
Kumbuka kwamba wakati sisi defined scalar line muhimu, hatukuwa na haja ya kuwa na wasiwasi kuhusu mwelekeo wa Curve ya ushirikiano. Vile vile ilikuwa kweli kwa integrals uso scalar: hatukuwa na haja ya kuwa na wasiwasi juu ya “mwelekeo” wa uso wa ushirikiano.
Kwa upande mwingine, wakati sisi defined vector line integrals, Curve ya ushirikiano zinahitajika mwelekeo. Hiyo ni, tulihitaji dhana ya curve iliyoelekezwa ili kufafanua mstari wa vector muhimu bila utata. Vile vile, tunapofafanua sehemu muhimu ya shamba la vector, tunahitaji wazo la uso unaoelekezwa. Uso unaoelekezwa unapewa mwelekeo wa “juu” au “chini” au, katika kesi ya nyuso kama nyanja au silinda, mwelekeo wa “nje” au “ndani”.
Hebu S iwe uso laini. Kwa hatua yoyote\((x,y,z)\) juu ya\(S\), tunaweza kutambua mbili kitengo wadudu kawaida\(\vecs N\) na\(-\vecs N\). Kama inawezekana kuchagua kitengo vector kawaida\(\vecs N\) katika kila hatua\((x,y,z)\) juu ya\(S\) hivyo kwamba\(\vecs N\) inatofautiana kuendelea juu\(S\), basi\(S\) ni “orientable.” Uchaguzi huo wa kitengo vector kawaida katika kila hatua inatoa mwelekeo wa uso\(S\). Ikiwa unafikiria shamba la kawaida kama kuelezea mtiririko wa maji, basi upande wa uso ambao maji hutembea kuelekea ni upande “hasi” na upande wa uso ambao maji hutoka ni upande “mzuri”. Kwa kawaida, uchaguzi wa mwelekeo hutoa upande\(S\) wa “nje” na upande wa “ndani” (au upande wa “juu” na upande wa “kushuka”), kama uchaguzi wa mwelekeo wa Curve hutoa maelekezo ya “mbele” na “nyuma”.
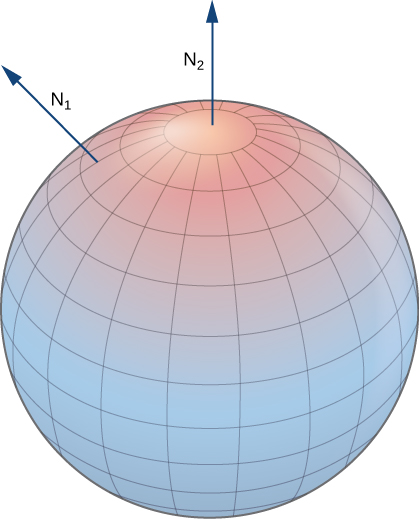
Nyuso zilizofungwa kama vile nyanja zinaelekezwa: ikiwa tunachagua vector ya kawaida ya nje kila hatua juu ya uso wa nyanja, basi kitengo vectors kawaida hutofautiana kwa kuendelea. Hii inaitwa mwelekeo mzuri wa uso uliofungwa (Kielelezo\(\PageIndex{18}\)). Pia tunaweza kuchagua vector ya kawaida ya ndani kila hatua ili kutoa mwelekeo wa “ndani”, ambayo ni mwelekeo hasi wa uso.
Sehemu ya grafu ya kazi yoyote ya laini pia\(z = f(x,y)\) inaelekezwa. Kama sisi kuchagua kitengo kawaida vector kwamba pointi “juu” uso katika kila hatua, basi kitengo vectors kawaida kutofautiana kuendelea juu ya uso. Tunaweza pia kuchagua kitengo kawaida vector kwamba pointi “chini” uso katika kila hatua. Ili kupata mwelekeo kama huo, sisi parameterize grafu ya\(f\) kwa njia ya kawaida:\(\vecs r(x,y) = \langle x,\, y, \, f(x,y)\rangle\), wapi\(x\) na\(y\) kutofautiana juu ya uwanja wa\(f\). Kisha,\(\vecs t_x = \langle 1,0,f_x \rangle\) na\(\vecs t_y = \langle 0,1,f_y \rangle \), na kwa hiyo bidhaa msalaba\(\vecs t_x \times \vecs t_y\) (ambayo ni ya kawaida kwa uso wakati wowote juu ya uso) ni\(\langle -f_x, \, -f_y, \, 1 \rangle \) Tangu\(z\) -sehemu ya vector hii ni moja, kitengo sambamba kawaida vector pointi “juu,” na upande wa juu wa uso huchaguliwa kuwa “chanya” upande.
Hebu\(S\) kuwa laini orientable uso na parameterization\(\vecs r(u,v)\). Kwa kila hatua\(\vecs r(a,b)\) juu ya uso, vectors\(\vecs t_u\) na\(\vecs t_v\) uongo katika ndege tangent wakati huo. Vector\(\vecs t_u \times \vecs t_v\) ni ya kawaida kwa ndege tangent katika\(\vecs r(a,b)\) na kwa hiyo ni ya kawaida kwa\(S\) wakati huo. Kwa hiyo, uchaguzi wa kitengo vector kawaida
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
inatoa mwelekeo wa uso\(S\).
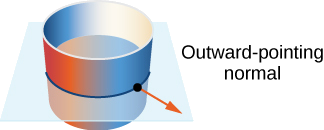
Kutoa mwelekeo wa silinda\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\).
Suluhisho
Uso huu una parameterization\(\vecs r(u,v) = \langle r \, \cos u, \, r \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h.\)
Vectors tangent ni\(\vecs t_u = \langle -r \, \sin u, \, r \, \cos u, \, 0 \rangle \) na\(\vecs t_v = \langle 0,0,1 \rangle\). Ili kupata mwelekeo wa uso, sisi compute kitengo kawaida vector
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
Katika kesi hiyo,\(\vecs t_u \times \vecs t_v = \langle r \, \cos u, \, r \, \sin u, \, 0 \rangle\) na kwa hiyo
\[||\vecs t_u \times \vecs t_v|| = \sqrt{r^2 \cos^2 u + r^2 \sin^2 u} = r. \nonumber \]
Mwelekeo wa silinda ni
\[\vecs N(u,v) = \dfrac{\langle r \, \cos u, \, r \, \sin u, \, 0 \rangle }{r} = \langle \cos u, \, \sin u, \, 0 \rangle. \nonumber \]
Angalia kwamba wadudu wote ni sawa na\(xy\) -ndege, ambayo inapaswa kuwa kesi na vectors ambayo ni ya kawaida kwa silinda. Zaidi ya hayo, wadudu wote wanasema nje, na kwa hiyo hii ni mwelekeo wa nje wa silinda (Kielelezo\(\PageIndex{19}\)).
Kutoa “juu” mwelekeo wa grafu ya\(f(x,y) = xy\).
- Kidokezo
-
Parameterize uso na kutumia ukweli kwamba uso ni grafu ya kazi.
- Jibu
-
\[\vecs{N}(x,y) = \left\langle \dfrac{-y}{\sqrt{1+x^2+y^2}}, \, \dfrac{-x}{\sqrt{1+x^2+y^2}}, \, \dfrac{1}{\sqrt{1+x^2+y^2}} \right\rangle \nonumber \]
Kwa kuwa kila Curve ina mwelekeo wa “mbele” na “nyuma” (au, katika kesi ya Curve imefungwa, mwelekeo wa saa na kinyume chake), inawezekana kutoa mwelekeo kwa curve yoyote. Kwa hiyo, inawezekana kufikiria kila curve kama curve oriented. Hii sio kwa nyuso, hata hivyo. Nyuso zingine haziwezi kuelekezwa; nyuso hizo huitwa zisizo na mwelekeo. Kimsingi, uso unaweza kuelekezwa ikiwa uso una upande wa “ndani” na upande wa “nje”, au upande wa “juu” na upande wa “chini”. Nyuso zingine zinajitokeza kwa namna hiyo kwamba hakuna dhana iliyoelezwa vizuri ya upande wa “ndani” au “nje”.
Mfano wa classic wa uso usio na mwelekeo ni mstari wa Möbius. Ili kuunda mstari wa Möbius, chukua mstari wa mstatili wa karatasi, fanya kipande cha karatasi ya nusu, na gundi mwisho pamoja (Kielelezo\(\PageIndex{20}\)). Kwa sababu ya nusu-twist katika strip, uso hauna “nje” upande au “ndani” upande. Ikiwa unafikiria kuweka vector ya kawaida kwa hatua kwenye mstari na kuwa na vector kusafiri njia yote karibu na bendi, basi (kwa sababu ya nusu-twist) vector pointi katika mwelekeo kinyume wakati anapata nyuma ya nafasi yake ya awali. Kwa hiyo, mstari huo una upande mmoja tu.

Kwa kuwa nyuso zingine hazipatikani, haiwezekani kufafanua uso wa vector muhimu kwenye nyuso zote za laini. Hii ni tofauti na integrals vector line, ambayo inaweza kuelezwa juu ya yoyote piecewise laini Curve.
Uso muhimu wa uwanja wa Vector
Kwa wazo la nyuso zinazoelekezwa mahali, sasa tuko tayari kufafanua sehemu muhimu ya shamba la vector. Ufafanuzi huo ni sawa na ufafanuzi wa mtiririko wa shamba la vector pamoja na safu ya ndege. Kumbuka kwamba kama\(\vecs{F}\) ni mbili-dimensional vector shamba na\(C\) ni ndege Curve, basi ufafanuzi wa flux ya\(\vecs{F}\) pamoja\(C\) kushiriki\(C\) katika vipande vidogo, kuchagua hatua ndani ya kila kipande, na kuhesabu\(\vecs{F} \cdot \vecs{N}\) katika hatua (wapi\(\vecs{N}\) kitengo vector kawaida katika hatua). Ufafanuzi wa uso muhimu wa uwanja wa vector unaendelea kwa mtindo huo, isipokuwa sasa tunakata uso\(S\) ndani ya vipande vidogo, chagua hatua katika kipande kidogo (mbili-dimensional), na uhesabu kwa\(\vecs{F} \cdot \vecs{N}\) hatua.
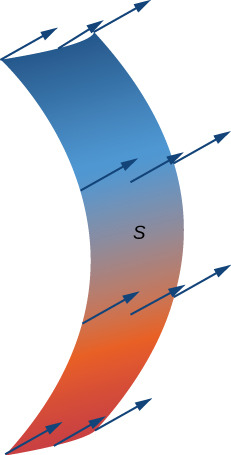
Ili kuweka ufafanuzi huu katika mazingira halisi ya ulimwengu, hebu\(S\) uwe na uso unaoelekezwa na vector ya kawaida ya kitengo\(\vecs{N}\). Hebu\(\vecs{v}\) kuwa shamba kasi ya maji inapita kupitia\(S\), na tuseme maji ina wiani\(\rho(x,y,z)\) Fikiria maji inapita kupitia\(S\), lakini\(S\) ni permit kabisa ili haina kuzuia mtiririko wa maji (Kielelezo\(\PageIndex{21}\)). Mzunguko mkubwa wa maji ni kiwango cha mtiririko wa wingi kwa eneo la kitengo. Flux ya wingi hupimwa kwa wingi kwa wakati wa kitengo kwa eneo la kitengo. Tunawezaje kuhesabu mzunguko wa wingi wa maji kote\(S\)?
Kiwango cha mtiririko, kipimo kwa wingi kwa wakati wa kitengo kwa eneo la kitengo, ni\(\rho \vecs N\). Ili kuhesabu mzunguko wa wingi kote\(S\), suka\(S\) vipande vidogo\(S_{ij}\). Ikiwa\(S_{ij}\) ni ndogo ya kutosha, basi inaweza kuhesabiwa na ndege ya tangent wakati fulani\(P\)\(S_{ij}\). Kwa hiyo, kitengo kawaida vector katika\(P\) inaweza kutumika kwa takriban\(\vecs N(x,y,z)\) katika kipande nzima\(S_{ij}\) kwa sababu vector kawaida kwa ndege haina mabadiliko kama sisi hoja katika ndege. Sehemu ya vector\(\rho v\) katika P katika mwelekeo wa\(\vecs{N}\) ni\(\rho \vecs v \cdot \vecs N\) saa\(P\). Kwa kuwa\(S_{ij}\) ni ndogo, bidhaa dot\(\rho v \cdot N\) mabadiliko kidogo sana kama sisi kutofautiana katika\(S_{ij}\) na kwa hiyo\(\rho \vecs v \cdot \vecs N\) inaweza kuchukuliwa kama takriban mara kwa mara katika\(S_{ij}\). Ili takriban wingi wa maji kwa wakati wa kitengo kinachozunguka\(S_{ij}\) (na sio tu ndani ya nchi\(P\)), tunahitaji kuzidisha\((\rho \vecs v \cdot \vecs N) (P)\) kwa eneo la\(S_{ij}\). Kwa hiyo, wingi wa maji kwa wakati wa kitengo unaozunguka\(S_{ij}\) katika mwelekeo wa\(\vecs{N}\) unaweza kuhesabiwa na\((\rho \vecs v \cdot \vecs N)\Delta S_{ij}\) wapi\(\vecs{N}\),\(\rho\) na wote\(\vecs{v}\) hupimwa\(P\) (Kielelezo\(\PageIndex{22}\)). Hii ni sawa na flux ya mbili-dimensional vector shamba\(\vecs{F}\) katika ndege Curve\(C\), ambapo sisi takriban flux katika kipande kidogo cha\(C\) na kujieleza\((\vecs{F} \cdot \vecs{N}) \,\Delta s\). Ili takriban mzunguko wa molekuli kote\(S\), fanya jumla
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
Kama vipande\(S_{ij}\) kupata ndogo, jumla
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij} \nonumber \]
anapata kiholela karibu na flux molekuli. Kwa hiyo, flux molekuli ni
\[\iint_s \rho \vecs v \cdot \vecs N \, dS = \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
Hii ni muhimu ya uso wa shamba la vector. Kuruhusu shamba la vector\(\rho \vecs{v}\) kuwa shamba la vector la kiholela\(\vecs{F}\) linasababisha ufafanuzi wafuatayo.
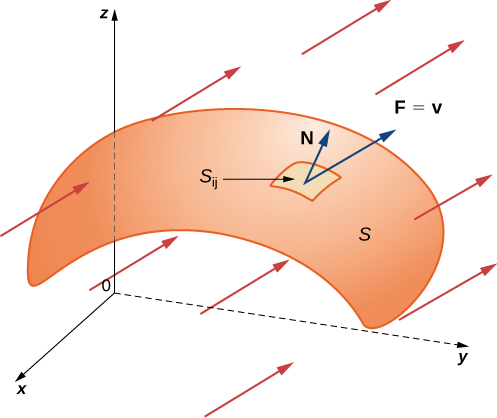
Hebu\(\vecs{F}\) kuendelea vector shamba na uwanja ambayo ina oriented uso\(S\) na kitengo vector kawaida\(\vecs{N}\). Sehemu muhimu ya\(\vecs{F}\) juu\(S\) ni
\[\iint_S \vecs{F} \cdot \vecs{S} = \iint_S \vecs{F} \cdot \vecs{N} \,dS. \label{surfaceI} \]
Angalia sambamba kati ya ufafanuzi huu na ufafanuzi wa vector line muhimu\(\displaystyle \int_C \vecs F \cdot \vecs N\, dS\). Sehemu muhimu ya uwanja wa vector hufafanuliwa kwa njia sawa na mstari wa flux muhimu katika pembe, isipokuwa uwanja wa ushirikiano ni uso (kitu cha pande mbili) badala ya pembe (kitu kimoja). Integral\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) inaitwa flux ya\(\vecs{F}\)\(S\) hela, kama muhimu\(\displaystyle \int_C \vecs F \cdot \vecs N\,dS\) ni flux ya\(\vecs F\) hela curve\(C\). Sehemu muhimu juu ya shamba la vector pia huitwa flux muhimu.
Kama vile kwa integrals vector line, uso muhimu\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) ni rahisi kukokotoa baada ya uso\(S\) imekuwa parameterized. Hebu\(\vecs r(u,v)\) kuwa parameterization ya\(S\) na uwanja wa parameter\(D\). Kisha, kitengo cha kawaida cha vector kinatolewa\(\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||}\) na, kutoka kwa Equation\ ref {SurfaceI}, tuna
\ [kuanza {align*}\ Int_c\ vecs F\ cdot\ vecs N\, ds &=\ Iint_s\ vecs F\ cdot\ dfrac {\ vecs t_u\ mara\ vecs t_v} {||\ vecs t_u\\ mara\ vecs t_v||}\, DS\\ [4pt]
&=\ Int_d\ kushoto (\ vecs F (\ vecs r (u, v)\ cdot\ dfrac {\ vecs t_u\ mara\ vecs t_v} {||\ vecs t_u\ mara\ vecs t_v||\ haki) ||\ vecs t_u \ mara\ vecs t_v ||\, da\\ [4pt]
&=\ iInt_d (\ vecs F (\ vecs r (u, v))\ cdot (\ vecs t_u\ mara\ vecs t_v))\, da. \ mwisho {align*}\]
Kwa hiyo, kukokotoa uso muhimu juu ya shamba vector tunaweza kutumia equation
\[\iint_S \vecs F \cdot \vecs N\, dS = \iint_D (\vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v)) \,dA. \label{equation 5} \]
Tumia sehemu muhimu ya uso
\[\iint_S \vecs F \cdot \vecs N\,dS, \nonumber \]
wapi\(\vecs{F} = \langle -y,x,0\rangle\) na\(S\) ni uso na parameterization
\[\vecs r(u,v) = \langle u,v^2 - u, \, u + v\rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 4. \nonumber \]
Suluhisho
Vectors tangent ni\(\vecs t_u = \langle 1,-1,1\rangle\) na\(\vecs t_v = \langle 0,2v,1\rangle\). Kwa hiyo,
\[\vecs t_u \times \vecs t_v = \langle -1 -2v, -1, 2v\rangle. \nonumber \]
Kwa Equation\ ref {equation 5},
\[ \begin{align*} \iint_S \vecs F \cdot dS &= \int_0^4 \int_0^3 F (\vecs r(u,v)) \cdot (\vecs t_u \times \vecs t_v) \, du \,dv \\[4pt] &= \int_0^4 \int_0^3 \langle u - v^2, \, u, \, 0\rangle \cdot \langle -1 -2v, \, -1, \, 2v\rangle \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 [(u - v^2)(-1-2v) - u] \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 (2v^3 + v^2 - 2uv - 2u) \, du\,dv \\[4pt] &= \int_0^4 \left.[2v^3u + v^2u - vu^2 - u^2]\right|_0^3 \, dv \\[4pt] &= \int_0^4 (6v^3 + 3v^2 - 9v - 9) \, dv \\[4pt] &= \left[ \dfrac{3v^4}{2} + v^3 - \dfrac{9v^2}{2} - 9v\right]_0^4\\[4pt] &= 340. \end{align*}\]
Kwa hiyo, mtiririko wa\(\vecs{F}\) hela\(S\) ni 340.
Mahesabu ya uso muhimu\[\iint_S \vecs F \cdot \vecs N \, dS, \nonumber \] ambapo\(\vecs F = \langle 0, -z, y \rangle\) na\(S\) ni sehemu ya nyanja kitengo katika octant kwanza na mwelekeo wa nje.
- Kidokezo
-
Tumia Equation\ ref {equation 5}.
- Jibu
-
0
Hebu\(\vecs v(x,y,z) = \langle 2x, \, 2y, \, z\rangle\) kuwakilisha shamba la kasi (pamoja na vitengo vya mita kwa pili) ya maji yenye wiani wa mara kwa mara 80 kg/m 3. Hebu\(S\) kuwa hemisphere\(x^2 + y^2 + z^2 = 9\) na\(z \leq 0\) vile ambavyo\(S\) vinaelekezwa nje. Pata kiwango cha mtiririko wa wingi wa maji kote\(S\).
Suluhisho
Parameterization ya uso ni
\[\vecs r(\phi, \theta) = \langle 3 \, \cos \theta \, \sin \phi, \, 3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi/2. \nonumber \]
Kama ilivyo katika Mfano, vectors tangent ni\(\vecs t_{\theta} = \langle -3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \theta \, \sin \phi, \, 0 \rangle \) na\( \vecs t_{\phi} = \langle 3 \, \cos \theta \, \cos \phi, \, 3 \, \sin \theta \, \cos \phi, \, -3 \, \sin \phi \rangle,\) na bidhaa zao msalaba ni
\[\vecs t_{\phi} \times \vecs t_{\theta} = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle. \nonumber \]
Angalia kwamba kila sehemu ya bidhaa ya msalaba ni chanya, na kwa hiyo vector hii inatoa mwelekeo wa nje. Kwa hiyo, tunatumia mwelekeo
\(\vecs N = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle \)
kwa ajili ya nyanja.
By\ studio {SurfaceI},
\ [kuanza {align*}\ iInt_s\ rho v\ cdot\, ds &= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} v (r (\ phi,\ theta))\ cdot (t_ {\ phi}\ mara t_ {\ theta})\, d\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2}\ langle 6\,\ cos\ theta\,\ dhambi\ phi,\, 6\,\ dhambi\ theta\,\ dhambi\ phi,\, 3\,\ cos\ phi\ rangle\ cdot\ langle 9\,\ cos\ theta\,\ dhambi ^ 2\ phi,\, 9\,\ dhambi\ theta\,\ dhambi ^ 2\ phi,\, 9\,\ dhambi\ phi\,\ cos\ phi\\ rangle\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ int_0^ ^ {\ pi/2} 54\,\ dhambi ^ 3\ phi + 27\,\ cos ^ 2\ phi\,\ dhambi\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\\ int_0^ {\ pi/2} 54 (1 -\ cos ^ 2\ phi)\,\ dhambi\ phi + 27\ cos^2\ phi\,\ dhambi\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54\,\ dhambi\ phi - 27\,\ cos ^ 2\ phi\,\ dhambi\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ Big [-54\,\ cos\ phi + 9\,\ cos ^ 3\ phi\ Big] _ {\ phi =0} ^ {\ phi=2\ pi}\, d\ theta\\
&=80\ int_0^ {2\ pi} 45\, d\ theta\\
&= 7200\ pi. \ mwisho {align*}\ nonumber\]
Kwa hiyo, kiwango cha mtiririko wa wingi ni\(7200\pi \, \text{kg/sec/m}^2\).
Hebu\(\vecs v(x,y,z) = \langle x^2 + y^2, \, z, \, 4y \rangle\) m/sec inawakilisha shamba la kasi la maji na wiani wa mara kwa mara 100 kg/m 3. Hebu\(S\) kuwa nusu-silinda\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) oriented nje. Tumia mzunguko wa wingi wa maji kote\(S\).
- Kidokezo
-
Tumia\ studio {SurfaceI}.
- Jibu
-
400 kg/sec/m
Katika Mfano\(\PageIndex{14}\), tumehesabu mzunguko wa wingi, ambayo ni kiwango cha mtiririko wa wingi kwa eneo la kitengo. Kama tunataka kupata kiwango cha mtiririko (kipimo kwa kiasi kwa wakati) badala yake, tunaweza kutumia flux muhimu
\[\iint_S \vecs v \cdot \vecs N \, dS, \nonumber \]
ambayo majani nje wiani. Kwa kuwa kiwango cha mtiririko wa maji hupimwa kwa kiasi kwa wakati wa kitengo, kiwango cha mtiririko haichukui molekuli. Kwa hiyo, tuna sifa zifuatazo za kiwango cha mtiririko wa maji na kasi\(\vecs v\) juu ya uso\(S\):
\[\text{Flow rate of fluid across S} = \iint_S \vecs v \cdot dS. \nonumber \]
Ili kukokotoa kiwango cha mtiririko wa maji katika Mfano, sisi tu kuondoa wiani mara kwa mara, ambayo inatoa kiwango cha mtiririko wa\(90 \pi \, m^3/sec\).
Wote flux wingi na kiwango cha mtiririko ni muhimu katika fizikia na uhandisi. Misa ya mzunguko hupima kiasi gani kinachozunguka juu ya uso; kiwango cha mtiririko hupima kiasi gani cha maji kinachozunguka juu ya uso.
Mbali na mfano wa mtiririko wa maji, integrals ya uso inaweza kutumika kutengeneza mtiririko wa joto. Tuseme kwamba joto\((x,y,z)\) katika hatua katika kitu ni\(T(x,y,z)\). Kisha mtiririko wa joto ni shamba la vector sawia na gradient hasi ya joto katika kitu. Ili kuwa sahihi, mtiririko wa joto hufafanuliwa kama shamba la vector\(F = - k \nabla T\), ambapo k mara kwa mara ni conductivity ya mafuta ya dutu ambayo kitu kinafanywa (mara kwa mara hii imedhamiriwa kwa majaribio). Kiwango cha mtiririko wa joto juu ya uso S katika kitu kinatolewa na uingizaji wa flux
\[\iint_S \vecs F \cdot dS = \iint_S -k \vecs \nabla T \cdot dS. \nonumber \]
Silinda imara ya chuma imetolewa na kutofautiana\(x^2 + y^2 \leq 1, \, 1 \leq z \leq 4\). Joto katika hatua\((x,y,z)\) katika kanda iliyo na silinda ni\(T(x,y,z) = (x^2 + y^2)z\). Kutokana na kwamba conductivity ya mafuta ya chuma cha kutupwa ni 55, pata mtiririko wa joto kwenye mipaka ya imara ikiwa mipaka hii inaelekezwa nje.
Suluhisho
Hebu\(S\) kuashiria mipaka ya kitu. Ili kupata mtiririko wa joto, tunahitaji kuhesabu Flux muhimu\[\iint_S -k\vecs \nabla T \cdot dS. \nonumber \] Taarifa ambayo\(S\) si uso laini lakini ni piecewise laini, tangu\(S\) ni muungano wa nyuso tatu laini (mviringo juu na chini, na upande cylindrical). Kwa hiyo, sisi mahesabu ya tatu integrals tofauti, moja kwa kila kipande laini ya\(S\). Kabla ya kuhesabu integrals yoyote, kumbuka kuwa gradient ya joto ni\(\vecs \nabla T = \langle 2xz, \, 2yz, \, x^2 + y^2 \rangle\).
Kwanza tunazingatia chini ya mviringo ya kitu, ambacho tunaashiria\(S_1\). Tunaweza kuona kwamba\(S_1\) ni mduara wa Radius 1 unaozingatia katika hatua\((0,0,1)\) ameketi katika ndege\(z = 1\). Uso huu una parameterization\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 1 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Kwa hiyo,
\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\)na\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle\), na\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0, \, 0, -v \rangle\).
Kwa kuwa uso unaelekezwa nje na\(S_1\) ni chini ya kitu, ni busara kwamba vector hii inaonyesha chini. Kwa Equation, mtiririko wa joto hela\(S_1\) ni
\[ \begin{align*}\iint_{S_1} -k \vecs \nabla T \cdot dS &= - 55 \int_0^{2\pi} \int_0^1 \vecs \nabla T(u,v) \cdot (\vecs t_u \times \vecs t_v) \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2 \cos^2 u + v^2 \sin^2 u \rangle \cdot \langle 0,0, -v\rangle \, dv \,du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2\rangle \cdot \langle 0, 0, -v \rangle \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 -v^3 \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} -\dfrac{1}{4} du \\[4pt] &= \dfrac{55\pi}{2}.\end{align*}\]
Sasa hebu tuchunguze juu ya mviringo ya kitu, ambacho tunaashiria\(S_2\). Tunaona kwamba\(S_2\) ni mduara wa radius 1 unaozingatia katika hatua\((0,0,4)\), ameketi katika ndege\(z = 4\). Uso huu una parameterization\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 4 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Kwa hiyo,\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\) na\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle \), na\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0,0,-v\rangle\).
Kwa kuwa uso ni oriented nje na\(S_1\) ni juu ya kitu, sisi badala kuchukua vector\(\vecs t_v \times \vecs t_u = \langle 0,0,v\rangle\). Kwa Equation, mtiririko wa joto hela\(S_1\) ni
\ [kuanza {align*}\ iint_ {S_2} -k\ vecs\ nabla T\ cdot ds &= - 55\ int_0^ {2\ pi}\ int_0 ^ 1\ vecs\ nabla T (u, v)\ cdot\, (\ vecs t_u\\ mara\ vecs t_v)\, dv\\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0 ^ 1\ angle 8v\,\ cos u,\, 8v\,\ sign u,\, v ^ 2\ cos^2 u + v ^ 2\ dhambi ^ 2 u\ rangle\ cdot\ angle 0,0, -v\ rangle\, dv\, du\\ [4pt]
&= - 55\ int_0 ^ {2\ pi}\ int_0 ^ 1\ langle 8v\,\ cos u,\, 8v\,\ dhambi u,\, v ^ 2\ rangle\ cdot\ langle 0, 0, -v\ rangle\,\, dv\, du\\ 4pt]
&= - 55\ int_0^ {2\ pi}\ int_0 ^ 1 -v ^ 3\, dv\, du = - 55\ int_0^ {2\ pi} -\ dfrac {1} {4}\, dfrac = -\ dfrac {55\ pi} {2}. \ mwisho {align*}\]
Mwisho, hebu tuchunguze upande wa cylindrical wa kitu. Uso huu una parameterization\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 1 \leq v \leq 4\). Kwa Mfano, tunajua kwamba\(\vecs t_u \times \vecs t_v = \langle \cos u, \, \sin u, \, 0 \rangle\). Kwa Equation,
\ [kuanza {align*}\ iint_ {S_3} -k\ vecs\ nabla T\ cdot ds &= - 55\ int_0^ {2\ pi}\ int_1 ^\ vecs\ nabla T (u, v)\ cdot (\ vecs t_u\\ mara\ vecs t_v)\, dv\\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_1 ^ 4\ angle 2v\,\ cos u,\, 2v\,\ sign u,\,\ cos ^ 2 u +\ dhambi ^ 2 u\ rangle\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0 ^ 1\ angle 2v\,\ cos ^ 2 u,\, 2v\,\ sin u,\, 0\ rangle\\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\, dv\,\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0 ^ 1 (2v\,\ cos ^ 2 u + 2v\,\ dhambi ^ 2 u)\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0 ^ 1 2v\, dv\\, du\\ [4pt]
&= -55\ int_0^ {2\ pi} du\\ [4pt]
&= -110\ pi. \ mwisho {align*}\]
Kwa hiyo, kiwango cha joto kati yake\(S\) ni
\[\dfrac{55\pi}{2} - \dfrac{55\pi}{2} - 110\pi = -110\pi. \nonumber \]
Mpira imara wa chuma unatolewa na kutofautiana\(x^2 + y^2 + z^2 \leq 1\). Joto katika hatua katika kanda iliyo na mpira ni\(T(x,y,z) = \dfrac{1}{3}(x^2 + y^2 + z^2)\). Pata mtiririko wa joto kwenye mipaka ya imara ikiwa mipaka hii inaelekezwa nje.
- Kidokezo
-
Fuata hatua za Mfano\(\PageIndex{15}\).
- Jibu
-
\(-\dfrac{440\pi}{3}\)
Dhana muhimu
- Nyuso zinaweza kuwa parameterized, kama vile curves inaweza parameterized. Kwa ujumla, nyuso zinapaswa kuwa parameterized na vigezo viwili.
- Nyuso zinaweza kuelekezwa wakati mwingine, kama vile curves zinaweza kuelekezwa. Nyuso zingine, kama vile mchoro wa Möbius, haziwezi kuelekezwa.
- Muhimu wa uso ni kama mstari muhimu katika mwelekeo mmoja wa juu. Uwanja wa ushirikiano wa uso muhimu ni uso katika ndege au nafasi, badala ya curve katika ndege au nafasi.
- Ufungashaji wa uso wa uso unaweza kuwa kazi ya scalar au shamba la vector. Kuhesabu uso muhimu na integrand yaani kazi, kutumia Equation. Kuhesabu uso muhimu na integrand yaani shamba vector, kutumia Equation.
- Ikiwa\(S\) ni uso, basi eneo la\(S\) ni\[\iint_S \, dS. \nonumber \]
Mlinganyo muhimu
- S calar uso muhimu
\[\iint_S f(x,y,z) \,dS = \iint_D f (\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA \nonumber \]
- Flux muhimu
\[\iint_S \vecs F \cdot \vecs N \, dS = \iint_S \vecs F \cdot dS = \iint_D \vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \nonumber \]
faharasa
- flux muhimu
- jina jingine kwa ajili ya uso muhimu ya shamba vector; mrefu kuliko katika fizikia na uhandisi
- curves gridi
- curves juu ya uso kwamba ni sambamba na mistari gridi ya taifa katika ndege kuratibu
- mtiririko wa joto
- uwanja wa vector sawia na gradient hasi joto katika kitu
- molekuli flux
- kiwango cha mtiririko mkubwa wa maji kwa eneo la kitengo, kipimo kwa wingi kwa wakati wa kitengo kwa eneo la kitengo
- mwelekeo wa uso
- ikiwa uso una upande wa “ndani” na upande wa “nje”, basi mwelekeo ni uchaguzi wa upande wa ndani au wa nje; uso unaweza pia kuwa na mwelekeo wa “juu” na “chini”
- parameter kikoa (parameter nafasi)
- kanda ya\(uv\) -ndege ambayo vigezo\(u\) na\(v\) kutofautiana kwa parameterization\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\)
- uso wa parameterized (uso wa parametric)
- uso uliotolewa na maelezo ya fomu\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\), ambapo vigezo\(u\) na\(v\) kutofautiana juu ya uwanja wa parameter katika\(uv\) -plane
- parameterization ya kawaida
- parameterization\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\) vile kwamba\(r_u \times r_v\) si sifuri kwa uhakika\((u,v)\) katika uwanja parameter
- eneo la uso
- eneo la uso\(S\) uliotolewa na uso muhimu\[\iint_S \,dS \nonumber \]
- uso muhimu
- muhimu ya kazi juu ya uso
- uso muhimu wa kazi ya thamani ya scalar
- muhimu ya uso ambayo integrand ni kazi ya scalar
- uso muhimu wa shamba la vector
- muhimu ya uso ambayo integrand ni shamba la vector



Inafuata kutoka Mfano\(\PageIndex{1}\) kwamba tunaweza parameterize mitungi yote ya fomu\(x^2 + y^2 = R^2\). Ikiwa S ni silinda iliyotolewa na equation\(x^2 + y^2 = R^2\), basi parameterization ya\(S\) ni\(\vecs r(u,v) = \langle R \, \cos u, \, R \, \sin u, \, v \rangle, \, 0 \leq u \leq 2 \pi, \, -\infty < v < \infty.\)
Tunaweza pia kupata aina tofauti za nyuso kutokana parameterization yao, au tunaweza kupata parameterization wakati sisi ni kupewa uso.
Mfano\(\PageIndex{2}\): Describing a Surface
Eleza uso\(S\) parameterized na\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u^2 \rangle, \, 0 \leq u < \infty, \, 0 \leq v < 2\pi\).
Suluhisho
Angalia kwamba ikiwa\(u\) inafanyika mara kwa mara, basi curve kusababisha ni mduara wa radius\(u\) katika ndege\(z = u\). Kwa hiyo, kama\(u\) ongezeko, radius ya mzunguko unaoongezeka huongezeka. Ikiwa\(v\) inafanyika mara kwa mara, basi curve kusababisha ni parabola wima. Kwa hiyo, tunatarajia uso kuwa paraboloid ya elliptic. Ili kuthibitisha hili, angalia kwamba
\[\begin{align*} x^2 + y^2 &= (u \, \cos v)^2 + (u \, \sin v)^2 \\[4pt] &= u^2 \cos^2 v + u^2 sin^2 v \\[4pt] &= u^2 \\[4pt] &=z\end{align*}\]
Kwa hiyo, uso ni paraboloid ya elliptic\(x^2 + y^2 = z\) (Kielelezo\(\PageIndex{3}\)).
Zoezi\(\PageIndex{2}\)
Eleza uso uliowekwa na\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, - \infty < u < \infty, \, 0 \leq v < 2\pi\).
Kushikilia\(u\) mara kwa mara na kuona ni aina gani ya matokeo ya curves. Fikiria kinachotokea kama\(u\) ongezeko au kupungua.
Koni\(x^2 + y^2 = z^2\)