Skip to main content
Global

16.5E: Mazoezi ya Sehemu ya 16.5

  1. Last updated
  2. Save as PDF
  • Page ID
    178926

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Kwa mazoezi yafuatayo, onyesha kama taarifa hiyo ni Kweli au ya Uongo.

    1. Ikiwa kazi za kuratibu za\(\vecs F : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) kuwa na derivatives ya pili ya sehemu, basi\(\text{curl} \, (\text{div} \,\vecs F)\) ni sawa na sifuri.

    2. \(\vecs\nabla \cdot (x \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z \,\mathbf{\hat k} ) = 1\).

    Jibu
    Uongo

    3. Mashamba yote ya vector ya fomu\(\vecs F(x,y,z) = f(x)\,\mathbf{\hat i} + g(y)\,\mathbf{\hat j} + h(z)\,\mathbf{\hat k}\) ni kihafidhina.

    4. Ikiwa\(\text{curl} \, \vecs F = \vecs 0\), basi\(\vecs F\) ni kihafidhina.

    Jibu
    Kweli

    5. Ikiwa\(\vecs F\) ni uwanja wa vector mara kwa mara basi\(\text{div} \,\vecs F = 0\).

    6. Ikiwa\(\vecs F\) ni uwanja wa vector mara kwa mara basi\(\text{curl} \,\vecs F =\vecs 0\).

    Jibu
    Kweli

    Kwa mazoezi yafuatayo, pata curl ya\(\vecs F\).

    7. \(\vecs F(x,y,z) = xy^2z^4\,\mathbf{\hat i} + (2x^2y + z)\,\mathbf{\hat j} + y^3 z^2\,\mathbf{\hat k}\)

    8. \(\vecs F(x,y,z) = x^2 z\,\mathbf{\hat i} + y^2 x\,\mathbf{\hat j} + (y + 2z)\,\mathbf{\hat k}\)

    Jibu
    \(\text{curl} \,\vecs F = \,\mathbf{\hat i} + x^2\,\mathbf{\hat j} + y^2\,\mathbf{\hat k}\)

    9. \(\vecs F(x,y,z) = 3xyz^2\,\mathbf{\hat i} + y^2 \sin z\,\mathbf{\hat j} + xe^{2z}\,\mathbf{\hat k}\)

    10. \(\vecs F(x,y,z) = x^2 yz\,\mathbf{\hat i} + xy^2 z\,\mathbf{\hat j} + xyz^2\,\mathbf{\hat k}\)

    Jibu
    \(\text{curl} \, \vecs F = (xz^2 - xy^2)\,\mathbf{\hat i} + (x^2 y - yz^2)\,\mathbf{\hat j} + (y^2z - x^2z)\,\mathbf{\hat k}\)

    11. \(\vecs F(x,y,z) = (x \, \cos y)\,\mathbf{\hat i} + xy^2\,\mathbf{\hat j}\)

    12. \(\vecs F(x,y,z) = (x - y)\,\mathbf{\hat i} + (y - z)\,\mathbf{\hat j} + (z - x)\,\mathbf{\hat k}\)

    Jibu
    \(\text{curl }\, \vecs F = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)

    13. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + x^2y^2z^2 \,\mathbf{\hat j} + y^2z^3 \,\mathbf{\hat k}\)

    14. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + yz \,\mathbf{\hat j} + xz \,\mathbf{\hat k}\)

    Jibu
    \(\text{curl }\, \vecs F = - y\,\mathbf{\hat i} - z \,\mathbf{\hat j} - x \,\mathbf{\hat k}\)

    15. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\)

    16. \(\vecs F(x,y,z) = ax\,\mathbf{\hat i} + by \,\mathbf{\hat j} + c \,\mathbf{\hat k}\)kwa vipindi\(a, \,b, \,c\).

    Jibu
    \(\text{curl }\, \vecs F = \vecs 0\)

    Kwa mazoezi yafuatayo, pata tofauti ya\(\vecs F\).

    17. \(\vecs F(x,y,z) = x^2 z\,\mathbf{\hat i} + y^2 x \,\mathbf{\hat j} + (y + 2z) \,\mathbf{\hat k}\)

    18. \(\vecs F(x,y,z) = 3xyz^2\,\mathbf{\hat i} + y^2 \sin z \,\mathbf{\hat j} + xe^2 \,\mathbf{\hat k}\)

    Jibu
    \(\text{div}\,\vecs F = 3yz^2 + 2y \, \sin z + 2xe^{2z}\)

    19. \(\vecs{F}(x,y) = (\sin x)\,\mathbf{\hat i} + (\cos y) \,\mathbf{\hat j}\)

    20. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\)

    Jibu
    \(\text{div}\,\vecs F = 2(x + y + z)\)

    21. \(\vecs F(x,y,z) = (x - y)\,\mathbf{\hat i} + (y - z) \,\mathbf{\hat j} + (z - x) \,\mathbf{\hat k}\)

    22. \(\vecs{F}(x,y) = \dfrac{x}{\sqrt{x^2+y^2}}\,\mathbf{\hat i} + \dfrac{y}{\sqrt{x^2+y^2}}\,\mathbf{\hat j}\)

    Jibu
    \(\text{div}\,\vecs F = \dfrac{1}{\sqrt{x^2+y^2}}\)

    23. \(\vecs{F}(x,y) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j}\)

    24. \(\vecs F(x,y,z) = ax\,\mathbf{\hat i} + by \,\mathbf{\hat j} + c \,\mathbf{\hat k}\)kwa vipindi\(a, \,b, \,c\).

    Jibu
    \(\text{div}\,\vecs F = a + b\)

    25. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + x^2y^2z^2\,\mathbf{\hat j} + y^2z^3\,\mathbf{\hat k}\)

    26. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + yz\,\mathbf{\hat j} + xz\,\mathbf{\hat k}\)

    Jibu
    \(\text{div}\,\vecs F = x + y + z\)

    Kwa mazoezi 27 & 28, kuamua kama kila moja ya kazi zilizopewa scalar ni harmonic.

    27. \(u(x,y,z) = e^{-x} (\cos y - \sin y)\)

    28. \(w(x,y,z) = (x^2 + y^2 + z^2)^{-1/2}\)

    Jibu
    Harmonic

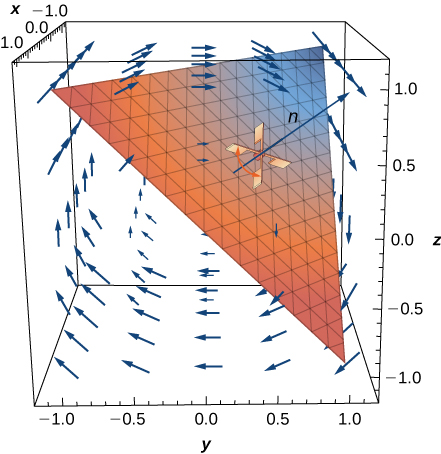
    29. Ikiwa\(\vecs F(x,y,z) = 2\,\mathbf{\hat i} + 2x j + 3y k\) na\(\vecs G(x,y,z) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j} + z \,\mathbf{\hat k}\), tafuta\(\text{curl} \, (\vecs F \times \vecs G)\).

    30. Ikiwa\(\vecs F(x,y,z) = 2\,\mathbf{\hat i} + 2x j + 3y k\) na\(\vecs G(x,y,z) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j} + z \,\mathbf{\hat k}\), tafuta\(\text{div} \, (\vecs F \times \vecs G)\).

    Jibu
    \(\text{div} \, (\vecs F \times \vecs G) = 2z + 3x\)

    31. Kupata\(\text{div} \,\vecs F\), kutokana na kwamba\(\vecs F = \vecs \nabla f\), wapi\(f(x,y,z) = xy^3z^2\).

    32. Kupata tofauti ya\(\vecs F\) kwa ajili ya uwanja vector\(\vecs F(x,y,z) = (y^2 + z^2) (x + y) \,\mathbf{\hat i} + (z^2 + x^2)(y + z) \,\mathbf{\hat j} + (x^2 + y^2)(z + x) \,\mathbf{\hat k}\).

    Jibu
    \(\text{div}\,\vecs F = 2r^2\)

    33. Kupata tofauti ya\(\vecs F\) kwa ajili ya uwanja vector\(\vecs F(x,y,z) = f_1(y,z)\,\mathbf{\hat i} + f_2 (x,z) \,\mathbf{\hat j} + f_3 (x,y) \,\mathbf{\hat k}\).

    Kwa mazoezi 34 - 36, matumizi\(r = |\vecs r|\) na\(\vecs r(x,y,z) = \langle x,y,z\rangle\).

    34. Kupata\(\text{curl} \, \vecs r\)

    Jibu
    \(\text{curl} \, \vecs r = \vecs 0\)

    35. Kupata\(\text{curl}\, \dfrac{\vecs r}{r}\).

    36. Kupata\(\text{curl}\, \dfrac{\vecs r}{r^3}\).

    Jibu
    \(\text{curl}\, \dfrac{\vecs r}{r^3} = \vecs 0\)

    37. Hebu\(\vecs{F}(x,y) = \dfrac{-y\,\mathbf{\hat i}+x\,\mathbf{\hat j}}{x^2+y^2}\), wapi\(\vecs F\) hufafanuliwa\(\big\{(x,y) \in \mathbb{R} | (x,y) \neq (0,0) \big\}\). Kupata\(\text{curl}\, \vecs F\).

    Kwa mazoezi yafuatayo, tumia mfumo wa algebra ya kompyuta ili kupata curl ya mashamba ya vector yaliyotolewa.

    38. [T]\(\vecs F(x,y,z) = \arctan \left(\dfrac{x}{y}\right)\,\mathbf{\hat i} + \ln \sqrt{x^2 + y^2} \,\mathbf{\hat j}+ \,\mathbf{\hat k}\)

    Jibu
    \(\text{curl }\, \vecs F = \dfrac{2x}{x^2+y^2}\,\mathbf{\hat k}\)

    39. [T]\(\vecs F(x,y,z) = \sin (x - y)\,\mathbf{\hat i} + \sin (y - z) \,\mathbf{\hat j} + \sin (z - x) \,\mathbf{\hat k}\)

    Kwa mazoezi yafuatayo, pata tofauti ya\(\vecs F\) wakati uliopewa.

    40. \(\vecs F(x,y,z) = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)katika\((2, -1, 3)\)

    Jibu
    \(\text{div}\,\vecs F = 0\)

    41. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z\,\mathbf{\hat k}\)katika\((1, 2, 3)\)

    42. \(\vecs F(x,y,z) = e^{-xy}\,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + e^{yz}\,\mathbf{\hat k}\)katika\((3, 2, 0)\)

    Jibu
    \(\text{div}\,\vecs F = 2 - 2e^{-6}\)

    43. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z\,\mathbf{\hat k}\)katika\((1, 2, 1)\)

    44. \(\vecs F(x,y,z) = e^x \sin y \,\mathbf{\hat i} - e^x \cos y\,\mathbf{\hat j} \)katika\((0, 0, 3)\)

    Jibu
    \(\text{div}\,\vecs F = 0\)

    Kwa mazoezi 45- 49, pata curl ya\(\vecs F\) wakati uliopewa.

    45. \(\vecs F(x,y,z) = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)katika\((2, -1, 3)\)

    46. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\)katika\((1, 2, 3)\)

    Jibu
    \(\text{curl }\, \vecs F = \mathbf{\hat j} - 3\,\mathbf{\hat k}\)

    47. \(\vecs F(x,y,z) = e^{-xy}\,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + e^{yz}\,\mathbf{\hat k}\)katika\((3, 2, 0)\)

    48. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\)katika\((1, 2, 1)\)

    Jibu
    \(\text{curl }\, \vecs F = 2\,\mathbf{\hat j} - \,\mathbf{\hat k}\)

    49. \(\vecs F(x,y,z) = e^x \sin y \,\mathbf{\hat i} - e^x \cos y\,\mathbf{\hat j} \)katika\((0, 0, 3)\)

    50. Hebu\(\vecs F(x,y,z) = (3x^2 y + az) \,\mathbf{\hat i} + x^3\,\mathbf{\hat j} + (3x + 3z^2)\,\mathbf{\hat k}\). Kwa thamani gani ya\(a\) ni\(\vecs F\) kihafidhina?

    Jibu
    \(a = 3\)

    51. Kutokana vector shamba\(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} \langle -y,x\rangle\) kwenye uwanja\(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}} = \big\{(x,y) \in \mathbb{R}^2 |(x,y) \neq (0,0) \big\}\), ni\(\vecs F\) kihafidhina?

    52. Kutokana vector shamba\(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} \langle x,y\rangle\) kwenye uwanja\(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}}\), ni\(\vecs F\) kihafidhina?

    Jibu
    \(\vecs F\)ni kihafidhina.

    53. Pata kazi iliyofanywa na uwanja wa nguvu\(\vecs{F}(x,y) = e^{-y}\,\mathbf{\hat i} - xe^{-y}\,\mathbf{\hat j}\) katika kusonga kitu kutoka\(P(0, 1)\) kwa\(Q(2, 0)\). Je, uwanja wa nguvu ni kihafidhina?

    54. Kokotoa tofauti\(\vecs F(x,y,z) = (\sinh x)\,\mathbf{\hat i} + (\cosh y)\,\mathbf{\hat j} - xyz\,\mathbf{\hat k}\).

    Jibu
    \(\text{div}\,\vecs F = \cosh x + \sinh y - xy\)

    55. kukokotoa\(\text{curl }\, \vecs F = (\sinh x)\,\mathbf{\hat i} + (\cosh y)\,\mathbf{\hat j} - xyz\,\mathbf{\hat k}\).

    Kwa mazoezi yafuatayo, fikiria mwili mgumu unaozunguka juu ya\(x\) -axis kinyume na kasi ya angular mara kwa mara\(\vecs \omega = \langle a,b,c \rangle\). Ikiwa\(P\) ni hatua katika mwili iko\(\vecs r = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\), kasi\(P\) inapewa na shamba la vector\(\vecs F = \vecs \omega \times \vecs r\).

    . The object is roughly a sphere with pointed ends on the x axis, which cuts it in half. An arrow r is drawn from (0,0,0) to P(x,y,z) and down from P(x,y,z) to the x axis." data-type="media" id="fs-id1167793480282">Mchoro wa mwelekeo wa tatu wa kitu kinachozunguka juu ya mhimili x kwa njia ya kinyume na kasi ya angular ya mara kwa mara w = <a, b, c. Kitu ni takribani nyanja na mwisho juu ya mhimili x, ambayo hupunguza kwa nusu. Mshale r hutolewa kutoka (0,0,0) hadi P (x, y, z) na chini kutoka P (x, y, z) hadi mhimili x." src="https://math.libretexts.org/@api/dek...16_05_201.jpeg">

    56. Express\(\vecs F\) in terms of \(\,\mathbf{\hat i},\;\,\mathbf{\hat j},\) and \(\,\mathbf{\hat k}\) vectors.

    Answer
    \(\vecs F = (bz - cy)\,\mathbf{\hat i}+(cx - az)\,\mathbf{\hat j} + (ay - bx)\,\mathbf{\hat k}\)

    57. Find \(\text{div} \, F\).

    58. Find \(\text{curl} \, F\)

    Answer
    \(\text{curl }\, \vecs F = 2\vecs\omega\)

    In the following exercises, suppose that \(\vecs \nabla \cdot \vecs F = 0\) and \(\vecs \nabla \cdot \vecs G = 0\).

    59. Does \(\vecs F + \vecs G\) necessarily have zero divergence?

    60. Does \(\vecs F \times \vecs G\) necessarily have zero divergence?

    Answer
    \(\vecs F \times \vecs G\) does not have zero divergence.

    In the following exercises, suppose a solid object in \(\mathbb{R}^3\) has a temperature distribution given by \(T(x,y,z)\). The heat flow vector field in the object is \(\vecs F = - k \vecs \nabla T\), where \(k > 0\) is a property of the material. The heat flow vector points in the direction opposite to that of the gradient, which is the direction of greatest temperature decrease. The divergence of the heat flow vector is \(\vecs \nabla \cdot \vecs F = -k \vecs \nabla \cdot \vecs \nabla T = - k \vecs \nabla^2 T\).

    61. Compute the heat flow vector field.

    62. Compute the divergence.

    Answer
    \(\vecs \nabla \cdot \vecs F = -200 k [1 + 2(x^2 + y^2 + z^2)] e^{-x^2+y^2+z^2}\)

    63. [T] Consider rotational velocity field \(\vecs v = \langle 0,10z, -10y \rangle\). If a paddlewheel is placed in plane \(x + y + z = 1\) with its axis normal to this plane, using a computer algebra system, calculate how fast the paddlewheel spins in revolutions per unit time.

    A three dimensional diagram of a rotational velocity field. The arrows are showing a rotation in a clockwise manner. A paddlewheel is shown in plan x + y + z = 1 with n extended out perpendicular to the plane.