16.5: Tofauti na Curl
- Page ID
- 178923
- Tambua tofauti kutoka kwa formula kwa shamba la vector lililopewa.
- Tambua curl kutoka kwa formula kwa shamba la vector lililopewa.
- Tumia mali ya curl na tofauti ili kuamua kama shamba la vector ni kihafidhina.
Katika sehemu hii, tunachunguza shughuli mbili muhimu kwenye uwanja wa vector: tofauti na curl. Wao ni muhimu kwa uwanja wa calculus kwa sababu kadhaa, ikiwa ni pamoja na matumizi ya curl na tofauti ili kuendeleza matoleo ya juu-dimensional ya Theorem ya Msingi ya Calculus. Aidha, curl na tofauti huonekana katika maelezo ya hisabati ya mechanics ya maji, electromagnetism, na nadharia ya elasticity, ambayo ni dhana muhimu katika fizikia na uhandisi. Tunaweza pia kutumia curl na tofauti kwa dhana nyingine ambazo tayari tumechunguza. Kwa mfano, chini ya hali fulani, shamba la vector ni kihafidhina ikiwa na tu ikiwa curl yake ni sifuri.
Mbali na kufafanua curl na tofauti, tunaangalia tafsiri fulani za kimwili, na kuonyesha uhusiano wao na mashamba ya vector ya kihafidhina na yasiyo ya chanzo.
Kugeuka
Tofauti ni operesheni kwenye uwanja wa vector ambayo inatuambia jinsi shamba hutenda kuelekea au mbali na hatua. Ndani ya nchi, tofauti ya shamba la vector\(\vecs{F}\) ndani\(\mathbb{R}^2\) au kwa\(\mathbb{R}^3\) hatua fulani\(P\) ni kipimo cha “kutoka-ness” ya shamba la vector saa\(P\). Ikiwa\(\vecs{F}\) inawakilisha kasi ya maji, basi tofauti ya\(\vecs{F}\) saa\(P\) inachukua kiwango cha wavu cha mabadiliko kuhusiana na wakati wa kiasi cha maji yanayotoka mbali na\(P\) (tabia ya maji ya mtiririko “nje ya” P). Hasa, ikiwa kiasi cha maji kinachoingia ndani\(P\) ni sawa na kiasi kinachotoka nje, basi tofauti\(P\) ni sifuri.
Ikiwa\(\vecs{F} = \langle P,Q,R \rangle\) ni shamba la vector\(P_x, \, Q_y, \) ndani\(\mathbb{R}^3\) na\(R_z\) zote zipo, basi tofauti ya\(\vecs{F}\) hufafanuliwa na
\[\begin{align} \text{div}\, F &= P_x + Q_y + R_z \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} + \dfrac{\partial R}{\partial z}. \end{align} \nonumber \]
Kumbuka tofauti ya shamba la vector sio shamba la vector, lakini kazi ya scalar. Kwa upande wa operator gradient
\[\vecs \nabla = \langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \rangle \nonumber \]
tofauti inaweza kuandikwa symbolically kama bidhaa dot
\[\text{div}\, \vecs F = \vecs \nabla \cdot \vecs{F}. \nonumber \]
Kumbuka hii ni nukuu tu kusaidia, kwa sababu bidhaa dot ya vector ya waendeshaji na vector ya kazi si maana defined kutokana na ufafanuzi wetu wa sasa wa bidhaa dot.
Ikiwa\(\vecs{F} = \langle P,Q \rangle\) ni shamba la vector katika\(\mathbb{R}^2\),\(P_x\) na\(Q_y\) zote mbili zipo, basi tofauti ya\(\vecs{F}\) hufafanuliwa sawa na
\[\begin{align*} \text{div}\, \vecs{F} &= P_x + Q_y \\[4pt] &= \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} \\[4pt] &= \vecs \nabla \cdot \vecs{F}. \end{align*}\]
Ili kuonyesha hatua hii, fikiria mashamba mawili ya vector katika Kielelezo\(\PageIndex{1}\). Kwa hatua yoyote, kiasi kinachozunguka ndani ni sawa na kiasi kinachotoka nje, hivyo kila wakati “kutoka-ness” ya shamba ni sifuri. Kwa hiyo, tunatarajia tofauti ya mashamba yote kuwa sifuri, na hii ni kweli kesi, kama
\[\text{div}(\langle 1,2 \rangle ) = \dfrac{\partial}{\partial x} (1) + \dfrac{\partial}{\partial y}(2) = 0 \nonumber \]
na
\[\text{div}(\langle -y,x \rangle ) = \dfrac{\partial}{\partial x} (-y) + \dfrac{\partial}{\partial y} (x) = 0. \nonumber \]
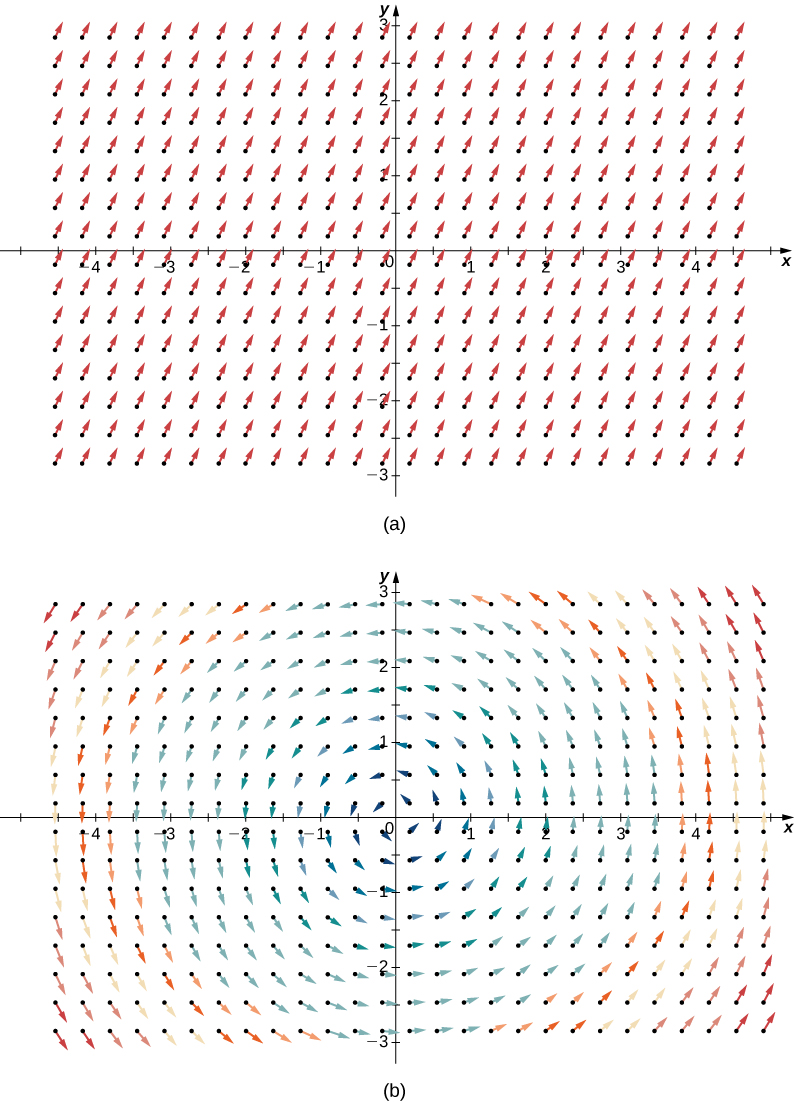
Kwa kulinganisha, fikiria uwanja wa vector radial\(\vecs{R} (x,y) = \langle -x, -y \rangle\) katika Kielelezo\(\PageIndex{2}\). Kwa hatua yoyote, maji mengi yanaingia ndani kuliko yanayotoka nje, na kwa hiyo “nje” ya shamba ni hasi. Tunatarajia tofauti ya uwanja huu kuwa hasi, na hii ni kweli kesi, kama
\[\text{div}(\vecs{R}) = \dfrac{\partial}{\partial x} (-x) + \dfrac{\partial}{\partial y} (-y) = -2. \nonumber \]
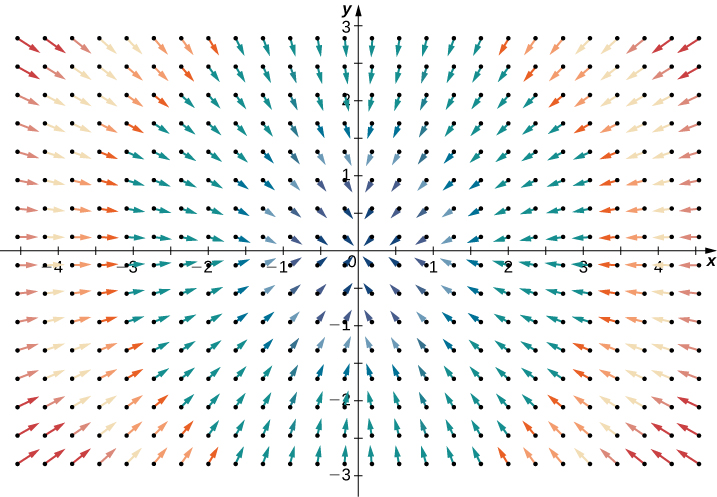
Ili kupata hisia ya kimataifa ya tofauti gani inatuambia, tuseme kwamba shamba la vector\(\mathbb{R}^2\) linawakilisha kasi ya maji. Fikiria kuchukua mduara wa elastic (mduara na sura ambayo inaweza kubadilishwa na shamba la vector) na kuiacha ndani ya maji. Ikiwa mduara unao eneo lake halisi kama inapita kupitia maji, basi tofauti ni sifuri. Hii ingekuwa kutokea kwa mashamba yote vector katika Kielelezo\(\PageIndex{1}\). Kwa upande mwingine, ikiwa umbo la mduara linapotoshwa ili eneo lake litapunguke au kuenea, basi tofauti si sifuri. Fikiria kuacha mduara huo wa elastic kwenye uwanja wa vector radial katika Kielelezo\(\PageIndex{2}\) ili katikati ya mduara iko kwenye hatua\((3, 3)\). Mduara ungetiririka kuelekea asili, na kama ilivyofanya hivyo mbele ya mduara ingesafiri polepole zaidi kuliko nyuma, na kusababisha mduara “scrunch” na kupoteza eneo. Hii ndio jinsi unavyoweza kuona tofauti hasi.
Ikiwa\(\vecs{F}(x,y,z) = e^x \hat{i} + yz \hat{j} - yz^2 \hat{k}\), basi pata tofauti ya\(\vecs{F}\) saa\((0,2,-1)\).
Suluhisho
Tofauti ya\(\vecs{F}\) ni
\[\dfrac{\partial}{\partial x} (e^x) + \dfrac{\partial}{\partial y}(yz) - \dfrac{\partial}{\partial z} (y z^2) = e^x + z - 2yz. \nonumber \]
Kwa hiyo, tofauti katika\((0,2,-1)\) ni\(e^0 - 1 + 4 = 4\). Ikiwa\(\vecs{F}\) inawakilisha kasi ya maji, basi maji mengi yanatoka nje kuliko inapita katika hatua\((0,2,-1)\).
Kupata\(\text{div}\, \vecs{F}\) kwa ajili ya
\[\vecs{F}(x,y,z) = \langle xy, \, 5-z^2, \, x^2 + y^2 \rangle \nonumber. \nonumber \]
- Kidokezo
-
Fuata Mfano\(\PageIndex{1}\).
- Jibu
-
\(\text{div}\, \vecs{F} = y \)
Programu nyingine ya kutofautiana ni kuchunguza kama shamba ni chanzo bure. Kumbuka kwamba shamba lisilo na chanzo ni shamba la vector ambalo lina kazi ya mkondo; sawa, shamba lisilo na chanzo ni shamba ambalo ni sifuri pamoja na safu yoyote iliyofungwa. Theorems mbili zifuatazo zinasema kwamba, chini ya hali fulani, mashamba ya vector yasiyo ya chanzo ni mashamba ya vector na tofauti ya sifuri.
Ikiwa\(\vecs{F} = \langle P,Q \rangle\) ni uwanja wa vector unaoendelea usio na chanzo na kazi za sehemu tofauti, basi\(\text{div}\, \vecs{F} = 0\).
Kwa kuwa\(\vecs{F}\) ni chanzo bure, kuna kazi\(g(x,y)\) na\(g_y = P\) na\(-g_x = Q\). Kwa hiyo,\(\vecs{F} = \langle g_y, -g_x \rangle\) na\(\text{div}\, \vecs{F} = g_{yx} - g_{xy} = 0\) kwa theorem ya Clairaut.
\(\square\)
Mazungumzo ya Tofauti ya Uwanja wa Vector ya Chanzo ni kweli kwenye mikoa iliyounganishwa tu, lakini ushahidi ni wa kiufundi sana kuingiza hapa. Hivyo, tuna theorem zifuatazo, ambayo inaweza kupima kama shamba vector katika\(\mathbb{R}^2\) ni chanzo bure.
Hebu\(\vecs{F} = \langle P,Q \rangle \) kuwa uwanja wa vector unaoendelea na kazi za sehemu tofauti na uwanja unaounganishwa tu. Kisha,\(\text{div}\, \vecs{F} = 0\) ikiwa na tu ikiwa\(\vecs{F}\) ni chanzo cha bure.
Je shamba\(\vecs{F} (x,y) = \langle x^2 y, \, 5 - xy^2 \rangle\) chanzo bure?
Suluhisho
Kumbuka uwanja wa\(\vecs{F}\) ni\(\mathbb{R}^2\) ambayo ni tu kushikamana. Zaidi ya hayo,\(\vecs{F}\) ni kuendelea na kazi differentiable sehemu. Kwa hiyo, tunaweza kutumia Mtihani wa Tofauti kwa Fields za Vector za Chanzo cha Chanzo ili kuchambua\(\vecs{F}\). Tofauti ya\(\vecs{F}\) ni
\[\dfrac{\partial}{\partial x} (x^2 y) + \dfrac{\partial}{\partial y} (5 - xy^2 ) = 2xy - 2xy = 0. \nonumber \]
Kwa hiyo,\(\vecs{F}\) ni chanzo bure na Divergence mtihani kwa Chanzo Free Vector Fields.
Hebu\(\vecs{F} (x,y) = \langle -ay, bx \rangle\) kuwa uwanja wa mzunguko ambapo\(a\) na\(b\) ni vyema vyema. Ni\(\vecs{F}\) chanzo bure?
- Kidokezo
-
Tumia tofauti.
- Jibu
-
Ndio
Kukumbuka kwamba aina flux ya theorem Green anasema kwamba
\[\oint_C \vecs F \cdot \vecs N \; ds = \iint_D P_x + Q_y \;dA, \nonumber \]
ambapo\(C\) ni rahisi kufungwa Curve na\(D\) ni kanda iliyoambatanishwa na\(C\). Tangu\(P_x + Q_y = \text{div}\,\vecs F\), Theorem ya Green wakati mwingine imeandikwa kama
\[\oint_C \vecs F \cdot \vecs N\; ds = \iint_D \text{div}\, \vecs F \;dA. \nonumber \]
Kwa hiyo, theorem ya Green inaweza kuandikwa kwa suala la tofauti. Ikiwa tunadhani ya tofauti kama derivative ya aina, basi theorem ya Green inasema “derivative” ya\(\vecs{F}\) kwenye kanda inaweza kutafsiriwa katika mstari muhimu wa\(\vecs{F}\) kando ya mipaka ya kanda. Hii ni sawa na Theorem ya Msingi ya Calculus, ambayo derivative ya kazi\(f\) kwenye sehemu ya mstari\([a,b]\) inaweza kutafsiriwa katika taarifa kuhusu\(f\) juu ya mipaka ya\([a,b]\). Kutumia tofauti, tunaweza kuona kwamba theorem ya Green ni analog ya juu-dimensional ya Theorem ya Msingi ya Calculus.
Tunaweza kutumia yote tuliyojifunza katika matumizi ya tofauti. Hebu\(\vecs{v}\) kuwa shamba la vector mfano wa kasi ya maji. Kwa kuwa tofauti ya hatua\(\vecs{v}\)\(P\) hatua “outflowing-ness” ya maji katika\(P\),\(\text{div}\, v(P) > 0\) ina maana kwamba maji zaidi inapita nje\(P\) kuliko inapita katika. Vile vile,\(\text{div}\, v(P) < 0\) inamaanisha maji mengi yanayotembea ndani ya\(P\) kuliko yanayotoka nje, na\(\text{div}\, \vecs{v}(P) = 0\) ina maana kiasi sawa cha maji kinachozunguka.
Tuseme\(\vecs{v}(x,y) = \langle -xy,y \rangle, \, y > 0\) mifano mtiririko wa maji. Je! Maji mengi yanayotembea katika hatua\((1,4)\) kuliko yanayotoka nje?
Suluhisho
Kuamua kama maji mengi yanaingia ndani\((1,4)\) kuliko yanayotoka nje, tunahesabu tofauti ya\(\vecs v\) saa\((1,4)\):
\[div(\vecs{v}) = \dfrac{\partial}{\partial x} (-xy) + \dfrac{\partial}{\partial y} (y) = -y + 1. \nonumber \]
Ili kupata tofauti katika\((1,4)\) mbadala hatua katika tofauti:\(-4 + 1 = -3\). Kwa kuwa tofauti ya\(\vecs v\) saa\((1,4)\) ni hasi, maji zaidi yanaingia ndani kuliko yanayotoka nje (Kielelezo\(\PageIndex{4}\)).

Kwa uwanja wa vector\(\vecs{v}(x,y) = \langle -xy, y \rangle , \, y > 0\), kupata pointi zote\(P\) kama kwamba kiasi cha maji inapita katika\(P\) sawa na kiasi cha maji inapita nje ya\(P\).
- Kidokezo
-
Pata ambapo tofauti ni sifuri.
- Jibu
-
All pointi kwenye mstari\(y = 1\).
Curl
Operesheni ya pili kwenye uwanja wa vector tunayochunguza ni curl, ambayo inachukua kiwango cha mzunguko wa shamba kuhusu hatua. Tuseme kwamba\(\vecs{F}\) inawakilisha shamba kasi ya maji. Kisha, curl ya\(\vecs{F}\) katika hatua\(P\) ni vector ambayo hatua ya tabia ya chembe\(P\) karibu na mzunguko juu ya mhimili kwamba pointi katika mwelekeo wa vector hii. Ukubwa wa vector curl kwa\(P\) hatua jinsi haraka chembe zinazunguka karibu na mhimili huu. Kwa maneno mengine, curl kwa hatua ni kipimo cha “spin” ya shamba la vector wakati huo. Kuangalia, fikiria kuweka paddlewheel ndani ya maji\(P\), na mhimili wa paddlewheel iliyokaa na vector curl (Kielelezo\(\PageIndex{5}\)). Curl inachukua tabia ya paddlewheel kugeuka.
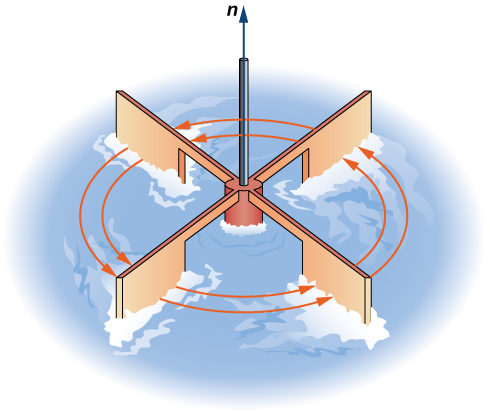
Fikiria mashamba ya vector katika Kielelezo\(\PageIndex{1}\). Katika sehemu (a), uwanja wa vector ni mara kwa mara na hakuna spin wakati wowote. Kwa hiyo, tunatarajia curl ya shamba kuwa sifuri, na hii ndiyo kweli. Sehemu (b) inaonyesha shamba la mzunguko, hivyo shamba lina spin. Hasa, ikiwa unaweka paddlewheel ndani ya shamba wakati wowote ili mhimili wa gurudumu uwe na ndege, gurudumu huzunguka kinyume chake. Kwa hiyo, tunatarajia curl ya shamba kuwa nonzero, na hii ni kweli kesi (curl ni\(2\,\mathbf{\hat k}\)).
Ili kuona nini curl ni kupima kimataifa, fikiria kuacha jani ndani ya maji. Kama jani linakwenda pamoja na mtiririko wa maji, curl inachukua tabia ya jani kugeuka. Kama curl ni sifuri, basi jani haina mzunguko kama hatua kwa njia ya maji.
Ikiwa\(\vecs{F} = \langle P,Q,R \rangle\) ni shamba la vector ndani\(\mathbb{R}^3\), na\(P_x, \, Q_y\), na\(R_z\) zote zipo, basi curl ya\(\vecs{F}\) inafafanuliwa na
\ [kuanza {align}\ maandishi {curl}\,\ vecs {F} &= (R_y - Q_z)\,\ mathbf {\ kofia i} + (P_z - R_x)\,\ mathbf {\ kofia j} + (Q_x - P_y)\,\ mathbf {\ kofia k}\\ [4pt]
&=\ kushoto (\ dfrac {\ sehemu R} {\ sehemu y} -\ dfrac {\ sehemu Q} {\ sehemu z}\ haki)\,\ mathbf {\ kofia i} +\ kushoto (\ dfrac {\ sehemu P} {\ sehemu z} -\ dfrac {\ sehemu R} {\ sehemu x}\ haki)\,\ mathbf {\ kofia j} +\ kushoto (\ dfrac {\ sehemu Q} {\ sehemu x} -\ dfrac {\ sehemu P} {\ sehemu y}\ haki)\,\ mathbf {\ kofia k}. \ mwisho {align}\ nonumber\]
Kumbuka kwamba curl ya shamba la vector ni shamba la vector, kinyume na tofauti.
Ufafanuzi wa curl inaweza kuwa vigumu kukumbuka. Ili kusaidia kwa kukumbuka, tunatumia notation\(\vecs \nabla \times \vecs{F}\) kusimama kwa “kuamua” ambayo inatoa formula curl:
\[\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \]
Maamuzi ya tumbo hii ni
\[(R_y - Q_z) \,\mathbf{\hat i} - (R_x - P_z) \,\mathbf{\hat j} + (Q_x - P_y) \,\mathbf{\hat k} = (R_y - Q_z) \,\mathbf{\hat i} + (P_z - R_x) \,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} = \text{curl}\, \vecs{F}. \nonumber \]
Hivyo, tumbo hili ni njia ya kusaidia kukumbuka formula ya curl. Kumbuka, ingawa, kwamba neno determinant hutumiwa sana loosely. determinant si kweli defined juu ya tumbo na entries kwamba ni wadudu tatu, waendeshaji tatu, na kazi tatu.
Kama\(\vecs{F} = \langle P,Q \rangle\) ni uwanja vector katika\(\mathbb{R}^2\), basi curl ya\(\vecs{F}\), kwa ufafanuzi, ni
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = \left(\dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right)\,\mathbf{\hat k}. \nonumber \]
Kupata curl ya\(\vecs{F}(P,Q,R) = \langle x^2 z, e^y + xz, xyz \rangle\).
Suluhisho
Curl ni
\[\begin{align*} \text{curl}\, f &= \vecs\nabla \times \vecs{F} \\ &= \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \partial/\partial x & \partial/\partial y & \partial / \partial z \\ P & Q & R \end{vmatrix} \\ &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\ &= (xz - x)\,\mathbf{\hat i} + (x^2 - yz)\,\mathbf{\hat j} + z \,\mathbf{\hat k}. \end{align*}\]
Pata curl ya\(\vecs{F} = \langle \sin x \, \cos z, \, \sin y \, \sin z, \, \cos x \, \cos y \rangle \) wakati\(\left(0, \dfrac{\pi}{2}, \dfrac{\pi}{2} \right)\).
- Kidokezo
-
Pata uamuzi wa tumbo\(\vecs \nabla \times \vecs{F}\).
- Jibu
-
\(-\hat{i}\)
Kupata curl ya\(\vecs{F} = \langle P,Q \rangle = \langle y,0\rangle\).
Suluhisho
Kumbuka kwamba uwanja huu vector lina wadudu kwamba wote ni sambamba. Kwa kweli, kila vector katika shamba ni sawa na x -axis. Ukweli huu unaweza kutuongoza kwenye hitimisho kwamba shamba halina spin na kwamba curl ni sifuri. Ili kupima nadharia hii, kumbuka kuwa
\[\text{curl}\, \vecs{F} = (Q_x - P_y)\,\mathbf{\hat k} = -\,\mathbf{\hat k} \neq \vecs 0. \nonumber \]
Kwa hiyo, uwanja huu wa vector una spin. Ili kuona kwa nini, fikiria kuweka paddlewheel wakati wowote katika quadrant ya kwanza (Kielelezo\(\PageIndex{6}\)). Ukubwa mkubwa wa vectors juu ya gurudumu husababisha gurudumu kugeuka. Gurudumu huzunguka katika mwelekeo wa saa (hasi), na kusababisha mgawo wa curl kuwa hasi.
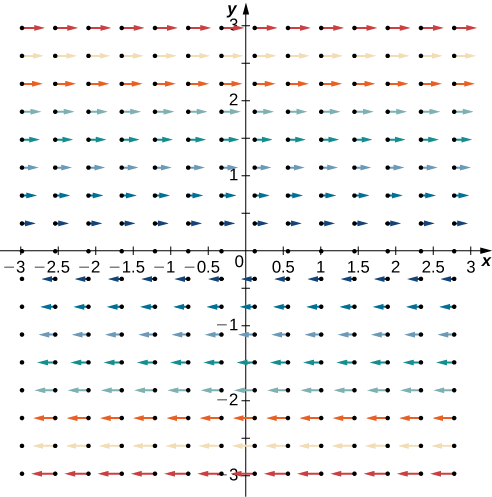
Kumbuka kwamba ikiwa\(\vecs{F} = \langle P,Q\rangle\) ni uwanja wa vector katika ndege, basi\(\text{curl}\, \vecs{F} \cdot \mathbf{\hat k} = (Q_x - P_y)\,\mathbf{\hat k} \cdot \mathbf{\hat k} = Q_x - P_y\). Kwa hiyo, aina ya mzunguko wa theorem ya Green wakati mwingine imeandikwa kama
\[\oint_C \vecs{F} \cdot d\vecs{r} = \iint_D \text{curl}\, \vecs F \cdot \,\mathbf{\hat k}\,dA, \nonumber \]
ambapo\(C\) ni rahisi kufungwa Curve na\(D\) ni kanda iliyoambatanishwa na\(C\). Kwa hiyo, fomu ya mzunguko wa theorem ya Green inaweza kuandikwa kwa suala la curl. Ikiwa tunadhani ya curl kama derivative ya aina, basi theorem ya Green inasema kuwa “derivative” ya\(\vecs{F}\) kwenye kanda inaweza kutafsiriwa katika mstari muhimu wa\(\vecs{F}\) kando ya mipaka ya kanda. Hii ni sawa na Theorem ya Msingi ya Calculus, ambayo derivative ya kazi\(f\) kwenye sehemu ya mstari\([a,b]\) inaweza kutafsiriwa katika taarifa kuhusu\(f\) juu ya mipaka ya\([a,b]\). Kutumia curl, tunaweza kuona fomu ya mzunguko wa theorem ya Green ni analog ya juu-dimensional ya Theorem ya Msingi ya Calculus.
Sasa tunaweza kutumia kile tulichojifunza kuhusu curl kuonyesha kwamba mashamba ya mvuto hayana “spin.” Tuseme kuna kitu katika asili na wingi\(m_1\) katika asili na kitu na wingi\(m_2\). Kumbuka kwamba nguvu ya mvuto ambayo kitu 1 kinaweka juu ya kitu cha 2 kinatolewa na shamba
\[ \vecs{F}(x,y,z) = - Gm_1m_2 \left\langle \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}, \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\right\rangle. \nonumber \]
Onyesha kwamba uwanja wa mvuto hauna spin.
Suluhisho
Ili kuonyesha kwamba\(\vecs{F}\) haina spin, tunahesabu curl yake. Hebu
- \(P(x,y,z) = \dfrac{x}{(x^2 + y^2 + z^2 )^{3/2}}\),
- \(Q(x,y,z) = \dfrac{y}{(x^2 + y^2 + z^2 )^{3/2}}\), na
- \(R(x,y,z) = \dfrac{z}{(x^2 + y^2 + z^2 )^{3/2}}\).
Kisha,
\ [kuanza {align*}\ Nakala {curl}\,\ vecs {F} &= - GM_1m_2 [(R_y - Q_z)\ mathbf {\ kofia i} + (P_z - R_x)\ mathbf {\ kofia j} + (Q_x - P_y)\ mathbf {\ kofia k}]\\ [4pt]
&= - GM_1m_2\ kuanza {pMatrix}\ kushoto (\ dfrac {-3yz} {(x ^ 2 + y ^ 2 + z ^ 2) ^ {5/2}} -\ kushoto (\ dfrac {-3yz} {(x ^ 2 + y ^ 2 + z ^ 2)\ haki)\ hisabati {\ kofia i}\ nonumber\\ [4pt]
+\ kushoto (\ dfrac {-3xz} {(x ^ 2 + y ^ 2 + z ^ 2) ^ {5/2}} -\ kushoto (\ dfrac {-3xz} {(x ^ 2 + y ^ 2 + z ^ 2)\ haki)\ haki)\ mathbf {\ kofia j}\ nonumber\\ [4pt]
+\ kushoto (\ dfrac {-3xy} {(x ^ 2 + y ^ 2 + z ^ 2) ^ {5/2}} -\ kushoto (\ dfrac {-3xy} {(x ^ 2 + y ^ 2 + z ^ 2) ^ {5/2}}\ haki)\ haki)\ mathbf {\ kofia k}\ mwisho {pmatrix}\\ [4pt]
&=\ vecs 0. \ mwisho {align*}\]
Kwa kuwa curl ya shamba la mvuto ni sifuri, shamba halina spin.
\(\vecs{v}(x,y) = \langle - \dfrac{y}{x^2+y^2}, \dfrac{x}{x^2+y^2} \rangle \)Mifano ya shamba mtiririko wa maji. Onyesha kwamba ikiwa unatupa jani ndani ya maji haya, kama jani linakwenda kwa muda, jani halizunguka.
- Kidokezo
-
Tumia curl.
- Jibu
-
\(\text{curl}\, \vecs{v} = \vecs 0\)
Kutumia Tofauti na Curl
Sasa kwa kuwa tunaelewa dhana za msingi za tofauti na curl, tunaweza kujadili mali zao na kuanzisha uhusiano kati yao na mashamba ya vector ya kihafidhina.
Kama\(\vecs{F}\) ni uwanja vector katika\(\mathbb{R}^3\) kisha curl ya pia\(\vecs{F}\) ni uwanja vector katika\(\mathbb{R}^3\). Kwa hiyo, tunaweza kuchukua tofauti ya curl. Theorem inayofuata inasema kuwa matokeo ni daima sifuri. Matokeo haya ni muhimu kwa sababu inatupa njia ya kuonyesha kwamba baadhi ya mashamba ya vector sio curl ya shamba lingine lolote. Ili kutoa matokeo haya tafsiri ya kimwili, kumbuka kuwa tofauti ya shamba la kasi kwa\(\vecs{v}\)\(P\) hatua hatua ya tabia ya maji yanayofanana yanayotoka\(P\). Kwa kuwa\(\text{div}(\text{curl}\,\vecs v) = 0\), kiwango cha mtiririko halisi katika uwanja wa vector\(\text{curl}\;\vecs v\) wakati wowote ni sifuri. Kuchukua curl ya uwanja wa vector\(\vecs{F}\) hupunguza chochote tofauti kilikuwapo\(\vecs{F}\).
Hebu\(\vecs{F} = \langle P,Q,R \rangle \) kuwa shamba la vector kwa\(\mathbb{R}^3\) vile kazi za sehemu zote zina derivatives ya pili ya pili ya utaratibu. Kisha,
\[\text{div}(\text{curl}\, \vecs{F}) = \vecs\nabla \cdot (\vecs \nabla \times \vecs F) = 0. \nonumber \]
Kwa ufafanuzi wa tofauti na curl, na kwa theorem ya Clairaut,
\[\begin{align*} \text{div}(\text{curl}\, \vecs{F}) = \text{div}[(R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k}] \\ = R_{yx} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy}\\ = 0. \end{align*}\]
\(\Box\)
Onyesha kwamba\(\vecs{F}(x,y,z) = e^x\,\mathbf{\hat i}+ yz\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\) sio curl ya shamba lingine la vector. Hiyo ni, onyesha kuwa hakuna vector nyingine\(\vecs{G}\) na\(\text{curl} \, \vecs G = \vecs F\).
Suluhisho
Kumbuka kwamba uwanja wa\(\vecs{F}\) ni wote wa\(\mathbb{R}^3\) na sehemu ya pili ili ya wote\(\vecs{F}\) ni kuendelea. Kwa hiyo, tunaweza kutumia theorem ya awali\(\vecs{F}\).
Tofauti ya sisi\(\vecs{F}\)\(e^x + z + 2xz\). Ikiwa\(\vecs{F}\) ilikuwa ni curl ya shamba la vector\(\vecs{G}\), basi\(\text{div}\, \vecs F = \text{div}(\text{curl} \,\vecs G) = 0\). Lakini, tofauti ya\(\vecs{F}\) sio sifuri, na kwa hiyo\(\vecs{F}\) sio curl ya shamba lolote la vector.
Je, inawezekana\(\vecs G(x,y,z) = \langle \sin x, \, \cos y, \, \sin (xyz)\rangle \) kwa kuwa curl ya shamba vector?
- Kidokezo
-
Kupata tofauti ya\(\vecs{G}\).
- Jibu
-
Hapana.
Kwa theorems mbili zifuatazo, tunaonyesha kwamba ikiwa\(\vecs{F}\) ni uwanja wa vector wa kihafidhina basi curl yake ni sifuri, na kama uwanja wa\(\vecs{F}\) ni kushikamana tu basi kuzungumza pia ni kweli. Hii inatupa njia nyingine ya kupima kama shamba la vector ni kihafidhina.
Ikiwa\(\vecs{F} = \langle P,Q,R\rangle\) ni kihafidhina, basi\(\text{curl} \, \vecs{F} = \vecs 0\).
Kwa kuwa mashamba ya vector ya kihafidhina yanakidhi mali ya msalaba-sehemu, sehemu zote za msalaba\(\vecs F\) ni sawa. Kwa hiyo,
\[\begin{align*} \text{curl}\, \vecs{F} &= (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \\[4pt] &= \vecs 0. \end{align*}\]
\(\Box\)
Theorem hiyo ni ya kweli kwa mashamba ya vector katika ndege.
Kwa kuwa shamba la vector la kihafidhina ni gradient ya kazi ya scalar, theorem ya awali inasema kuwa\(\text{curl}\, (\vecs \nabla f) = \vecs 0\) kwa kazi yoyote ya scalar\(f\). Kwa upande wa notation yetu ya curl,\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\). Equation hii mantiki kwa sababu bidhaa msalaba wa vector na yenyewe daima ni zero vector. Wakati mwingine equation\(\vecs \nabla \times \vecs \nabla (f) = \vecs 0\) ni rahisi kama\(\vecs \nabla \times \vecs \nabla = \vecs 0\).
Hebu\(\vecs{F} = \langle P,Q,R\rangle\) kuwa uwanja wa vector katika nafasi kwenye uwanja uliounganishwa tu. Ikiwa\(\text{curl}\;\vecs F = \vecs 0\), basi\(\vecs{F}\) ni kihafidhina.
tangu\(\text{curl}\, \vecs F = \vecs 0\), tuna kwamba\(R_y = Q_z, \, P_z = R_x\), na\(Q_x = P_y\). Kwa hiyo,\(\vecs{F}\) inatimiza mali ya msalaba-sehemu kwenye uwanja unaounganishwa tu, na Mali ya Msalaba wa Mashamba ya Kihafidhina ina maana kwamba\(\vecs{F}\) ni kihafidhina.
\(\Box\)
Theorem hiyo pia ni kweli katika ndege. Kwa hiyo, ikiwa\(\vecs{F}\) ni uwanja wa vector katika ndege au katika nafasi na uwanja unaunganishwa tu, basi\(\vecs{F}\) ni kihafidhina ikiwa na tu ikiwa\(\text{curl}\, \vecs F = \vecs 0\).
Tumia curl kuamua kama\(\vecs{F}(x,y,z) = \langle yz, xz, xy\rangle\) ni kihafidhina.
Suluhisho
Kumbuka kuwa uwanja wa\(\vecs{F}\) ni yote\(\mathbb{R}^3\) ambayo ni kushikamana tu (Kielelezo\(\PageIndex{7}\)). Kwa hiyo, tunaweza kupima kama\(\vecs{F}\) ni kihafidhina kwa kuhesabu curl yake.
Curl ya\(\vecs{F}\) ni
\[\left(\dfrac{\partial}{\partial y}xy - \dfrac{\partial}{\partial z} xz \right) \,\mathbf{\hat i} + \left(\dfrac{\partial}{\partial y}yz - \dfrac{\partial}{\partial z} xy \right) \,\mathbf{\hat j} + \left(\dfrac{\partial}{\partial y}xz - \dfrac{\partial}{\partial z} yz \right)\,\mathbf{\hat k}= (x - x)\,\mathbf{\hat i} + (y - y)\,\mathbf{\hat j} + (z - z)\,\mathbf{\hat k} = \vecs 0. \nonumber \]
Hivyo,\(\vecs{F}\) ni kihafidhina.
Tumeona kwamba curl ya gradient ni sifuri. Je, ni tofauti gani ya gradient? Ikiwa\(f\) ni kazi ya vigezo viwili, basi\(\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy}\). Sisi vifupisho hii “mara mbili dot bidhaa” kama\(\vecs \nabla^2\). Operator hii inaitwa operator Laplace, na katika equation hii notation Laplace inakuwa\(\vecs \nabla^2 f = 0\). Kwa hiyo, kazi ya harmonic ni kazi ambayo inakuwa sifuri baada ya kuchukua tofauti ya gradient.
Vile vile, kama\(f\) ni kazi ya vigezo tatu basi
\[\text{div}(\vecs \nabla f) = \vecs \nabla \cdot (\vecs \nabla f) = f_{xx} + f_{yy} + f_{zz}. \nonumber \]
Kutumia nukuu hii tunapata equation Laplace kwa ajili ya kazi harmonic ya vigezo tatu:
\[\vecs \nabla^2 f = 0. \nonumber \]
Kazi za harmonic hutokea katika programu nyingi. Kwa mfano, kazi ya uwezo wa uwanja wa umeme katika eneo la nafasi ambayo haina malipo ya tuli ni harmonic.
Je, inawezekana\(f(x,y) = x^2 + x - y\) kwa kuwa kazi ya uwezo wa shamba la umeme ambalo liko katika eneo la\(\mathbb{R}^2\) bure la malipo ya tuli?
Suluhisho
Kama\(f\) walikuwa kama kazi uwezo, basi\(f\) itakuwa harmonic. Kumbuka kwamba\(f_{xx} = 2\) na\(f_{yy} = 0\), na hivyo\(f_{xx} + f_{yy} \neq 0\). Kwa hiyo,\(f\) si harmonic na\(f\) hawezi kuwakilisha uwezo umeme.
Je, inawezekana\(f(x,y) = x^2 - y^2 + x\) kwa kazi kuwa kazi ya uwezo wa uwanja wa umeme ulio katika eneo la\(\mathbb{R}^2\) bure la malipo ya tuli?
- Kidokezo
-
Kuamua kama kazi ni harmonic.
- Jibu
-
Ndiyo.
Dhana muhimu
- Tofauti ya shamba la vector ni kazi ya scalar. Tofauti hupima “kutoka-ness” ya shamba la vector. Ikiwa\(\vecs{v}\) ni shamba la kasi la maji, basi tofauti ya\(\vecs{v}\) wakati fulani ni outflow ya maji chini ya uingiaji wakati huo.
- Curl ya shamba la vector ni shamba la vector. Curl ya uwanja wa vector katika\(P\) hatua hatua ya tabia ya chembe katika mzunguko juu ya mhimili kwamba pointi katika mwelekeo wa curl katika\(P\).\(P\)
- Shamba la vector na kikoa kilichounganishwa tu ni kihafidhina ikiwa na tu ikiwa curl yake ni sifuri.
Mlinganyo muhimu
- Curl
\[\vecs \nabla \times \vecs{F} = (R_y - Q_z)\,\mathbf{\hat i} + (P_z - R_x)\,\mathbf{\hat j} + (Q_x - P_y)\,\mathbf{\hat k} \nonumber \]
- Kugeuka
\[\vecs \nabla \cdot \vecs{F} = P_x + Q_y + R_z\nonumber \]
- Tofauti ya curl ni sifuri
\[\vecs \nabla \cdot (\vecs \nabla \times \vecs F) = 0\nonumber \]
- Curl ya gradient ni vector sifuri
\[\vecs \nabla \times (\vecs \nabla f) = 0 \nonumber \]
faharasa
- curl
- curl ya shamba la vector\(\vecs{F}=⟨P,Q,R⟩\), iliyoashiria\(\vecs ∇× \vecs{F}\) ni “kuamua” ya tumbo\[\begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}. \nonumber \] na hutolewa kwa maneno\((R_y−Q_z)\,\mathbf{\hat i} +(P_z−R_x)\,\mathbf{\hat j} +(Q_x−P_y)\,\mathbf{\hat k} \); inachukua tabia ya chembe kwa hatua ya kugeuka juu ya mhimili unaoelezea mwelekeo wa curl kwa uhakika
- muachano
- tofauti ya shamba la vector\(\vecs{F}=⟨P,Q,R⟩\), iliyoashiria\(\vecs ∇× \vecs{F}\), ni\(P_x+Q_y+R_z\); inachukua “upungufu” wa shamba la vector



Programu moja ya kutofautiana hutokea katika fizikia, wakati wa kufanya kazi na mashamba ya magnetic. Shamba la magnetic ni shamba la vector ambalo linaashiria ushawishi wa mikondo ya umeme na vifaa vya magnetic. Wataalamu wa Fizikia hutumia tofauti katika sheria ya Gauss kwa sumaku, ambayo inasema kwamba ikiwa\(\vecs{B}\) ni shamba la magnetic, basi\(\vecs \nabla \cdot \vecs{B} = 0\); kwa maneno mengine, tofauti ya shamba la magnetic ni sifuri.
Mfano\(\PageIndex{2}\): Determining Whether a Field Is Magnetic
Je, inawezekana\(\vecs{F} (x,y) = \langle x^2 y, \, y - xy^2 \rangle \) kwa kuwa shamba magnetic?
Suluhisho
Ikiwa\(\vecs{F}\) ingekuwa magnetic, basi tofauti yake itakuwa sifuri. Tofauti ya\(\vecs{F}\) ni
\[\dfrac{\partial}{\partial x} (x^2y) + \dfrac{\partial}{\partial y} (y - xy^2) = 2 xy + 1 - 2 xy = 1 \nonumber \]
na kwa hiyo\(\vecs{F}\) hawezi mfano wa shamba la magnetic (Kielelezo\(\PageIndex{3}\)).