16.1: Mashamba ya vector
- Page ID
- 178930
- Tambua uwanja wa vector katika ndege au katika nafasi.
- Mchoro shamba vector kutoka equation kupewa.
- Tambua shamba la kihafidhina na kazi yake inayohusishwa.
Mashamba ya vector ni chombo muhimu cha kuelezea dhana nyingi za kimwili, kama vile gravitation na electromagnetism, ambayo huathiri tabia ya vitu juu ya eneo kubwa la ndege au ya nafasi. Pia ni muhimu kwa kushughulika na tabia kubwa kama vile dhoruba za anga au mikondo ya bahari ya kina-bahari. Katika sehemu hii, sisi kuchunguza ufafanuzi wa msingi na grafu ya mashamba vector ili tuweze kujifunza yao kwa undani zaidi katika mapumziko ya sura hii.
Mifano ya Fields
Tunawezaje kuiga mfano wa nguvu ya mvuto inayotokana na vitu vingi vya astronomia? Tunawezaje kuiga kasi ya chembe za maji juu ya uso wa mto? Kielelezo\(\PageIndex{1}\) hutoa uwakilishi wa kuona wa matukio kama hayo.
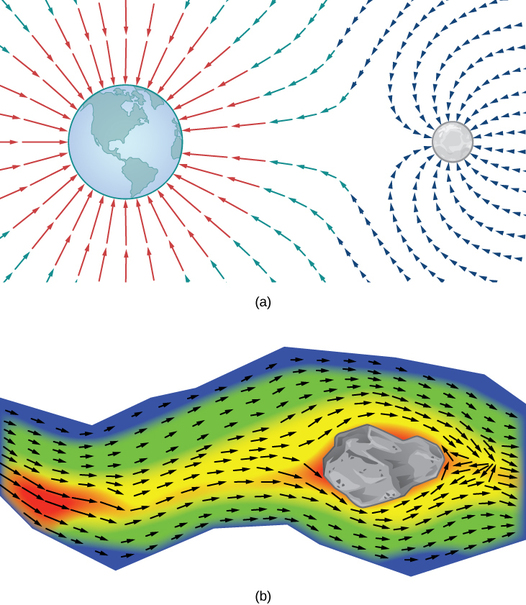
Kielelezo\(\PageIndex{1a}\) kinaonyesha uwanja wa mvuto unaofanywa na vitu viwili vya astronomia, kama vile nyota na sayari au sayari na mwezi. Kwa hatua yoyote katika takwimu, vector inayohusishwa na hatua inatoa nguvu ya mvuto halisi inayotumiwa na vitu viwili kwenye kitu cha kitengo cha kitengo. Vectors ya ukubwa mkubwa katika takwimu ni vectors karibu na kitu kikubwa. Kitu kikubwa kina molekuli kubwa, hivyo kina nguvu ya mvuto wa ukubwa mkubwa kuliko kitu kidogo.
Kielelezo\(\PageIndex{1b}\) kinaonyesha kasi ya mto kwenye pointi juu ya uso wake. Vector inayohusishwa na hatua fulani juu ya uso wa mto hutoa kasi ya maji wakati huo. Kwa kuwa vectors upande wa kushoto wa takwimu ni ndogo kwa ukubwa, maji yanapita polepole kwenye sehemu hiyo ya uso. Kama maji huenda kutoka kushoto kwenda kulia, hukutana na baadhi ya rapids karibu na mwamba. Kasi ya maji huongezeka, na whirlpool hutokea katika sehemu ya rapids.
Kila takwimu inaonyesha mfano wa shamba vector. Intuitively, uwanja wa vector ni ramani ya vectors. Katika sehemu hii, tunasoma mashamba ya vector\(ℝ^2\) na\(ℝ^3\).
- uwanja vector\(\vecs{F}\) katika\(ℝ^2\) ni kazi ya vector mbili-dimensional\(\vecs{F}(x,y)\) kwa kila hatua\((x,y)\) ya subset\(D\) ya\(ℝ^2\). Subset\(D\) ni uwanja wa shamba la vector.
- uwanja vector\(\vecs{F}\) katika\(ℝ^3\) ni kazi ya vector tatu-dimensional\(\vecs{F}(x,y,z)\) kwa kila hatua\((x,y,z)\) ya subset\(D\) ya\(ℝ^3\). Subset\(D\) ni uwanja wa shamba la vector.
Vector mashamba katika\(ℝ^2\)
Shamba la vector\(ℝ^2\) ndani linaweza kuwakilishwa katika mojawapo ya njia mbili sawa. Njia ya kwanza ni kutumia vector na vipengele ambavyo ni kazi mbili za kutofautiana:
\[\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩ \nonumber \]
Njia ya pili ni kutumia vectors kitengo cha kawaida:
\[\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}. \nonumber \]
Shamba la vector linasemekana kuwa linaendelea ikiwa kazi zake za sehemu zinaendelea.
Hebu\(\vecs{F} (x,y)=(2y^2+x−4)\,\hat{\mathbf i}+\cos(x)\,\hat{\mathbf j}\) kuwa uwanja wa vector katika\(ℝ^2\). Kumbuka kuwa hii ni mfano wa uwanja unaoendelea wa vector tangu kazi zote mbili za sehemu zinaendelea. Ni vector gani inayohusishwa na uhakika\((0,−1)\)?
Suluhisho
Badilisha maadili ya uhakika\(x\) na\(y\):
\[\begin{align*} \vecs{F} (0,-1) &=(2{(−1)}^2+0−4) \,\hat{\mathbf i}+\cos(0) \,\hat{\mathbf j} \\[4pt] &=−2 \,\hat{\mathbf i} + \hat{\mathbf j}. \end{align*}\]
Hebu\(\vecs{G}(x,y)=x^2y\,\hat{\mathbf i}−(x+y)\,\hat{\mathbf j}\) kuwa uwanja wa vector katika\(ℝ^2\). Ni vector gani inayohusishwa na uhakika\((−2,3)\)?
- Kidokezo
-
Badilisha maadili ya uhakika katika kazi ya vector.
- Jibu
-
\(\vecs{G}(−2,3)=12\hat{\mathbf i}−\hat{\mathbf j}\)
Kuchora uwanja wa Vector
Sasa tunaweza kuwakilisha shamba la vector kulingana na vipengele vyake vya kazi au vectors ya kitengo, lakini kuiwakilisha kwa kuibua kwa kuchora ni ngumu zaidi kwa sababu uwanja wa shamba la vector iko\(ℝ^2\), kama ilivyo. Kwa hiyo “grafu” ya shamba la vector katika\(ℝ^2\) maisha katika nafasi nne. Kwa kuwa hatuwezi kuwakilisha nafasi nne-dimensional kuibua, sisi badala yake kuteka mashamba vector\(ℝ^2\) katika ndege yenyewe. Ili kufanya hivyo, futa vector inayohusishwa na hatua fulani wakati wa ndege. Kwa mfano, tuseme vector kuhusishwa na uhakika\((4,−1)\) ni\(⟨3,1⟩\). Kisha, tunataka kuteka vector\(⟨3,1⟩\) katika hatua\((4,−1)\).
Tunapaswa kupanga vectors kutosha kuona sura ya jumla, lakini sio wengi kwamba mchoro unakuwa fujo la jumbled. Ikiwa tungependa kupanga vector ya picha kila mahali katika kanda, ingeweza kujaza kanda kabisa na haina maana. Badala yake, tunaweza kuchagua pointi kwenye makutano ya mistari ya gridi ya taifa na kupanga sampuli ya vectors kadhaa kutoka kila roboduara ya mfumo wa kuratibu mstatili\(ℝ^2\).
Kuna aina mbili za mashamba ya vector ambayo sura hii inalenga: mashamba ya radial na mashamba ya mzunguko.\(ℝ^2\) Mashamba ya radial mfano wa mashamba fulani ya mvuto na mashamba ya chanzo cha nishati, na mashamba ya mzunguko mfano wa harakati ya maji katika vortex. Katika uwanja wa radial, wadudu wote huelekeza moja kwa moja kuelekea au moja kwa moja mbali na asili. Aidha, ukubwa wa vector yoyote inategemea tu umbali wake kutoka asili. Katika uwanja wa radial, vector iko kwenye hatua\((x,y)\) ni perpendicular kwa mduara unaozingatia asili ambayo ina uhakika\((x,y)\), na wadudu wengine wote kwenye mduara huu wana ukubwa sawa.
Mchoro uwanja wa vector\(\vecs{F} (x,y)=\dfrac{x}{2}\hat{\mathbf i}+\dfrac{y}{2}\hat{\mathbf j}\).
Suluhisho
Ili mchoro uwanja huu wa vector, chagua sampuli ya pointi kutoka kila roboduara na ukokote vector inayofanana. Jedwali lifuatayo linatoa sampuli ya mwakilishi wa pointi katika ndege na vectors sambamba.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ (x, y)\)” style="wima align:katikati; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨\dfrac{1}{2},0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨1,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,\dfrac{1}{2}⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,1⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−\dfrac{1}{2},0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−1,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,−1⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
Kielelezo\(\PageIndex{2a}\) kinaonyesha shamba la vector. Kuona kwamba kila vector ni perpendicular kwa mduara sambamba, Kielelezo\(\PageIndex{2b}\) inaonyesha duru overlain kwenye uwanja vector.
Chora shamba la radial\(\vecs{F} (x,y)=−\dfrac{x}{3}\hat{\mathbf i}−\dfrac{y}{3}\hat{\mathbf j}\).
- Kidokezo
-
Mchoro vectors kutosha kupata wazo la sura.
- Jibu
-

Tofauti na mashamba ya radial, katika uwanja wa mzunguko, vector katika hatua\((x,y)\) ni tangent (si perpendicular) kwa mduara na radius\(r=\sqrt{x^2+y^2}\). Katika uwanja wa mzunguko wa kawaida, wadudu wote wanasema ama kwa mwelekeo wa saa au kwa mwelekeo wa kinyume, na ukubwa wa vector inategemea tu umbali wake kutoka kwa asili. Wote wa mifano zifuatazo ni clockwise mzunguko mashamba, na tunaona kutoka uwakilishi wao Visual kwamba wadudu kuonekana mzunguko kuzunguka asili.
Mchoro uwanja wa vector\(\vecs{F} (x,y)=⟨y,\,−x⟩\).
Suluhisho
Unda meza (angalia moja inayofuata) kwa kutumia sampuli ya mwakilishi wa pointi katika ndege na vectors zao zinazofanana. Kielelezo\(\PageIndex{3}\) kinaonyesha uwanja wa vector unaosababisha.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ (x, y)\)” style="wima align:katikati; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,−1⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,−2⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨1,−1⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨1,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨2,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨1,1⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,1⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,2⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−1,1⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−1,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−2,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−1,−1⟩\) |
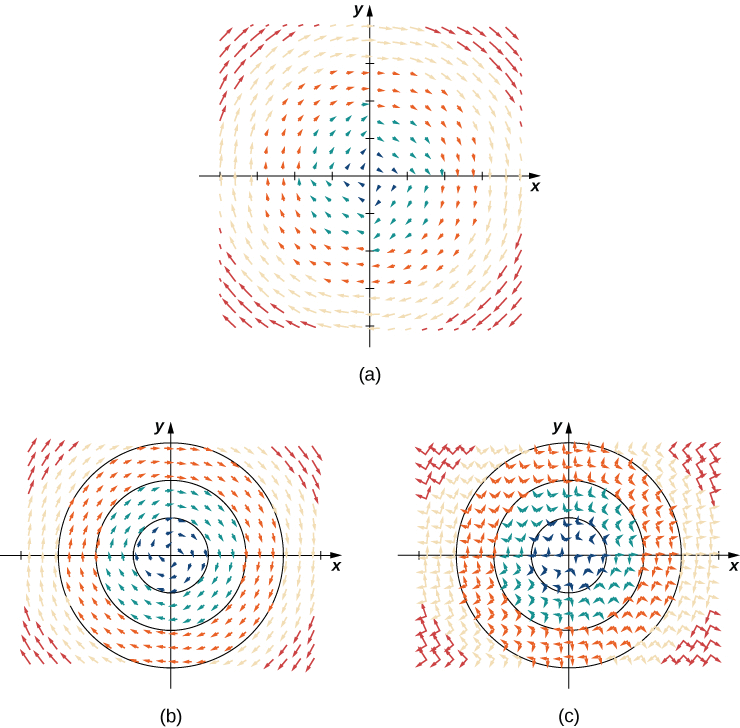
Uchambuzi
Kumbuka kwamba vector\(\vecs{F}(a,b)=⟨b,−a⟩\) pointi clockwise na perpendicular kwa vector\(⟨a,b⟩\) radial (Tunaweza kuthibitisha madai haya kwa kompyuta dot bidhaa ya wadudu wawili:\(⟨a,b⟩·⟨−b,a⟩=−ab+ab=0\).) Zaidi ya hayo, vector\(⟨b,−a⟩\) ina urefu\(r=\sqrt{a^2+b^2}\). Kwa hiyo, tuna maelezo kamili ya uwanja huu wa mzunguko wa vector: vector inayohusishwa na uhakika\((a,b)\) ni vector na urefu r tangent kwa mduara na r radius, na inaonyesha katika mwelekeo wa saa.
Mchoro kama vile kwamba katika Kielelezo mara nyingi\(\PageIndex{3}\) hutumika kuchambua mifumo kuu ya dhoruba, ikiwa ni pamoja na vimbunga na vimbunga. Katika ulimwengu wa kaskazini, dhoruba huzunguka kinyume chake; katika ulimwengu wa kusini, dhoruba huzunguka saa moja kwa moja. (Hii ni athari inayosababishwa na mzunguko wa Dunia kuhusu mhimili wake na inaitwa Athari ya Coriolis.)

Mchoro vector shamba\(\vecs{F}(x,y)=\dfrac{y}{x^2+y^2}\hat{\mathbf i}, -\dfrac{x}{x^2+y^2}\hat{\mathbf j}\).
Suluhisho
Ili kutazama shamba hili la vector, kwanza kumbuka kuwa bidhaa ya dot\(\vecs{F}(a,b)·(a \,\hat{\mathbf i}+b \,\hat{\mathbf j})\) ni sifuri kwa hatua yoyote\((a,b)\). Kwa hiyo, kila vector ni tangent kwa mduara ambayo iko. Pia, kama\((a,b)\rightarrow(0,0)\), ukubwa wa\(\vecs{F}(a,b)\) huenda kwa infinity. Ili kuona hili, kumbuka kuwa
\(||\vecs{F}(a,b)||=\sqrt{\dfrac{a^2+b^2}{ {(a^2+b^2)}^2 }} =\sqrt{\dfrac{1}{a^2+b^2}}\).
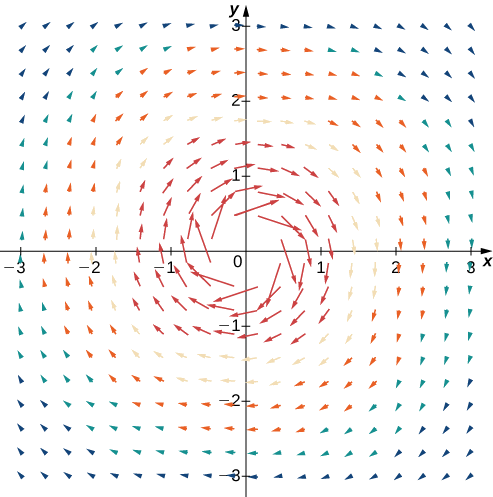
Tangu\(\dfrac{1}{a^2+b^2}\rightarrow \infty\) kama\((a,b)\rightarrow (0,0)\), basi\(||\vecs F(a,b)||\rightarrow \infty\) kama\((a,b)\rightarrow (0,0)\). Sehemu hii ya vector inaonekana sawa na uwanja wa vector katika Mfano\(\PageIndex{3}\), lakini katika kesi hii ukubwa wa vectors karibu na asili ni kubwa. Jedwali\(\PageIndex{3}\) inaonyesha sampuli ya pointi na wadudu sambamba, na Kielelezo\(\PageIndex{5}\) inaonyesha uwanja vector. Kumbuka kuwa uwanja huu vector mifano whirlpool mwendo wa mto katika Kielelezo\(\PageIndex{5}\) (b). uwanja wa uwanja huu vector ni wote\(ℝ^2\) isipokuwa kwa uhakika\((0,0)\).
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ (x, y)\)” style="wima align:katikati; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,−1⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨1,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨\dfrac{1}{2},0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,1⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨0,\dfrac{1}{2}⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)” style="wima align:katikati; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−1,0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−\dfrac{1}{2},0⟩\) | \ (x, y)\)” style="wima align:katikati; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)” style="wima align:katikati; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
Mchoro vector shamba\(\vecs{F}(x,y)=⟨−2y,\,2x⟩\). Je, shamba la vector ni radial, rotational, au wala?
- Kidokezo
-
Mbadala pointi\(\vecs{F}\) kutosha katika kupata wazo la sura.
- Jibu
-
Mzunguko

Tuseme kwamba\(\vecs{v} (x,y)=−\dfrac{2y}{x^2+y^2}\hat{\mathbf i}+\dfrac{2x}{x^2+y^2}\hat{\mathbf j}\) ni shamba kasi ya maji. Je! Maji yanahamia kwa kasi gani\((1,−1)\)? (Kudhani vitengo vya kasi ni mita kwa pili.)
Suluhisho
Ili kupata kasi ya maji kwa uhakika\((1,−1)\), badala ya uhakika katika\(\vecs{v} \):
\(\vecs{v}(1,−1)=\dfrac{−2(−1)}{1+1}\hat{\mathbf i}+\dfrac{2(1)}{1+1}\hat{\mathbf j}=\hat{\mathbf i}+\hat{\mathbf j}\).
Kasi ya maji katika\((1,−1)\) ni ukubwa wa vector hii. Kwa hiyo, kasi ni\(||\hat{\mathbf i}+\hat{\mathbf j}||=\sqrt{2}\) m/sec.
Vector shamba\(\vecs{v} (x,y)=⟨4|x|,\,1⟩\) mifano kasi ya maji juu ya uso wa mto. Je! Kasi ya maji ni nini\((2,3)\)? Tumia mita kwa sekunde kama vitengo.
- Kidokezo
-
Kumbuka, kasi ni ukubwa wa kasi.
- Jibu
-
\(\sqrt{65}\)m/sec
Sisi kuchunguza mashamba vector ambayo yana wadudu wa magnitudes mbalimbali, lakini kama tuna kitengo wadudu, tunaweza pia kuwa na kitengo vector shamba. Shamba la vector\(\vecs{F}\) ni shamba la vector kitengo ikiwa ukubwa wa kila vector katika shamba ni 1. Katika uwanja wa vector kitengo, habari pekee muhimu ni mwelekeo wa kila vector.
Onyesha kuwa uwanja wa vector\(\vecs{F} (x,y)=\left\langle\dfrac{y}{\sqrt{x^2+y^2}},−\dfrac{x}{\sqrt{x^2+y^2}}\right\rangle\) ni uwanja wa vector wa kitengo.
Suluhisho
Ili kuonyesha kwamba\(\vecs{F}\) ni shamba la kitengo, lazima tuonyeshe kwamba ukubwa wa kila vector ni\(1\). Kumbuka kwamba
\[\begin{align*} \sqrt{ \left(\dfrac{y}{\sqrt{x^2+y^2}}\right)^2+\left(−\dfrac{x}{\sqrt{x^2+y^2}}\right)^2} &=\sqrt{ \dfrac{y^2}{x^2+y^2}+\dfrac{x^2}{x^2+y^2}} \\[4pt] &=\sqrt{\dfrac{x^2+y^2}{x^2+y^2}} \\[4pt] &=1 \end{align*}\]
Kwa hiyo,\(\vecs{F} \) ni kitengo vector shamba.
Je vector shamba\(\vecs{F} (x,y)=⟨−y,\,x⟩\) kitengo vector shamba?
- Kidokezo
-
Tumia ukubwa wa kwa\(\vecs{F} \) hatua ya kiholela\((x,y)\).
- Jibu
-
Hapana.
Kwa nini mashamba ya vector ya kitengo ni muhimu? Tuseme tunasoma mtiririko wa maji, na tunajali tu kuhusu mwelekeo ambao maji yanapita kwa hatua fulani. Katika kesi hiyo, kasi ya maji (ambayo ni ukubwa wa vector ya kasi inayofanana) haina maana, kwa sababu yote tunayojali ni mwelekeo wa kila vector. Kwa hiyo, kitengo vector shamba kuhusishwa na kasi ni shamba tunataka kujifunza.
Ikiwa\(\vecs{F} =⟨P,Q,R⟩\) ni shamba la vector, basi uwanja wa vector wa kitengo cha sambamba ni\(\big\langle\tfrac{P}{||\vecs F||},\tfrac{Q}{||\vecs F||},\tfrac{R}{||\vecs F||}\big\rangle\). Kumbuka kwamba ikiwa\(\vecs{F}(x,y)=⟨y,\,−x⟩\) ni shamba la vector kutoka Mfano\(\PageIndex{6}\), basi ukubwa wa\(\vecs{F} \) ni\(\sqrt{x^2+y^2}\), na kwa hiyo uwanja wa vector wa kitengo sambamba ni shamba\(\vecs{G} \) kutoka kwa mfano uliopita.
Ikiwa\(\vecs{F} \) ni shamba la vector, basi mchakato wa kugawa\(\vecs{F} \) kwa ukubwa wake kuunda shamba la vector kitengo\(\vecs{F}/||\vecs{F}||\) inaitwa normalizing shamba\(\vecs{F} \).
Vector mashamba katika\(ℝ^3\)
Tumeona mifano kadhaa ya mashamba vector katika\(ℝ^2\); hebu sasa kurejea mawazo yetu kwa mashamba vector katika\(ℝ^3\). Mashamba haya ya vector yanaweza kutumika kutengeneza mashamba ya mvuto au sumakuumeme, na pia yanaweza kutumika kutengeneza mtiririko wa maji au mtiririko wa joto katika vipimo vitatu. Sehemu ya vector mbili-dimensional inaweza kweli tu mfano wa harakati ya maji kwenye kipande mbili-dimensional ya mto (kama vile uso wa mto). Kwa kuwa mto unapita kupitia vipimo vitatu vya anga, ili kuiga mtiririko wa kina kirefu cha mto, tunahitaji shamba la vector katika vipimo vitatu.
Mwelekeo wa ziada wa shamba tatu-dimensional unaweza kufanya mashamba ya vector kuwa vigumu\(ℝ^3\) zaidi kutazama, lakini wazo ni sawa. Ili kutazama shamba la vector ndani\(ℝ^3\), njama ya vectors ya kutosha ili kuonyesha sura ya jumla. Tunaweza kutumia njia sawa ya kutazama shamba la vector\(ℝ^2\) kwa kuchagua pointi katika kila octant.
Kama vile kwa mashamba vector katika\(ℝ^2\), tunaweza kuwakilisha mashamba vector katika\(ℝ^3\) na kazi sehemu. Tunahitaji tu kazi ya ziada ya sehemu kwa mwelekeo wa ziada. Tunaandika ama
\[\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩ \nonumber \]
au
\[\vecs{F}(x,y,z)=P(x,y,z)\hat{\mathbf i}+Q(x,y,z)\hat{\mathbf j}+R(x,y,z)\hat{\mathbf k}. \nonumber \]
Eleza uwanja wa vector\(\vecs{F}(x,y,z)=⟨1,\,1,\,z⟩\).
Suluhisho
Kwa uwanja huu wa vector,\(x\) -na\(y\) -vipengele ni mara kwa mara, hivyo kila hatua katika\(ℝ^3\) ina vector kuhusishwa na\(x\) - na\(y\) -vipengele sawa na moja. Ili kutazama\(\vecs{F}\), sisi kwanza tunazingatia kile shamba inaonekana kama katika\(xy\) -plane. Ndani ya\(xy\) ndege,\(z=0\). Kwa hiyo, kila hatua ya fomu\((a,b,0)\) ina vector\(⟨1,1,0⟩\) inayohusishwa nayo. Kwa pointi si katika\(xy\) -plane lakini kidogo juu yake, vector kuhusishwa ina ndogo lakini chanya\(z\) -sehemu, na hivyo kuhusishwa vector pointi kidogo zaidi. Kwa pointi ambazo ziko juu ya\(xy\) ndege,\(z\) -sehemu ni kubwa, hivyo vector ni karibu wima. Kielelezo\(\PageIndex{6}\) kinaonyesha uwanja huu wa vector.
Kielelezo\(\PageIndex{6}\): uwakilishi Visual ya uwanja vector\(\vecs{F}(x,y,z)=⟨1,1,z⟩\).
Mchoro vector shamba\(\vecs{G}(x,y,z)=⟨2,\,\dfrac{z}{2},\,1⟩\).
- Kidokezo
-
Badilisha pointi za kutosha kwenye uwanja wa vector ili kupata wazo la sura ya jumla.
- Jibu
Katika mfano unaofuata, tunachunguza moja ya matukio ya classic ya shamba la vector tatu-dimensional: shamba la mvuto.
Sheria ya Newton ya gravitation inasema kwamba\(\vecs{F}=−G\dfrac{m_1m_2}{r^2}\hat{\mathbf r}\), ambapo G ni mara kwa mara ya mvuto wa ulimwengu wote. Inaelezea uwanja wa mvuto unaofanywa na kitu (kitu 1) cha wingi\(m_1\) kilicho kwenye asili kwenye kitu kingine (kitu 2) cha wingi\(m_2\) kilicho kwenye hatua\((x,y,z)\). Shamba\(\vecs{F}\) inaashiria nguvu ya mvuto ambayo kitu 1 kinaweka juu ya kitu 2,\(r\) ni umbali kati ya vitu viwili, na\(\hat{\mathbf r}\) inaonyesha vector kitengo kutoka kitu cha kwanza hadi cha pili. Ishara ndogo inaonyesha kwamba nguvu ya mvuto huvutia kuelekea asili; yaani, nguvu ya kitu 1 inavutia. Mchoro shamba vector kuhusishwa na equation hii.
Suluhisho
Kwa kuwa kitu 1 iko katika asili, umbali kati ya vitu hutolewa na\(r=\sqrt{x^2+y^2+z^2}\). kitengo vector kutoka kitu 1 kwa kitu 2 ni\(\hat{\mathbf r}=\dfrac{⟨x,y,z⟩}{||⟨x,y,z⟩||}\), na hivyo\(\hat{\mathbf r}=\big\langle\dfrac{x}{r},\dfrac{y}{r},\dfrac{z}{r}\big\rangle\). Kwa hiyo, mvuto vector\(\vecs{F}\) shamba exerted na kitu 1 juu ya kitu 2 ni
\[ \vecs{F}=−Gm_1m_2\big\langle\dfrac{x}{r^3},\dfrac{y}{r^3},\dfrac{z}{r^3}\big\rangle. \nonumber \]
Huu ni mfano wa uwanja wa vector radial katika\(ℝ^3\).
Kielelezo\(\PageIndex{7}\) kinaonyesha nini uwanja huu wa mvuto inaonekana kama kwa wingi mkubwa katika asili. Kumbuka kwamba ukubwa wa vectors huongezeka kama vectors wanakaribia asili.
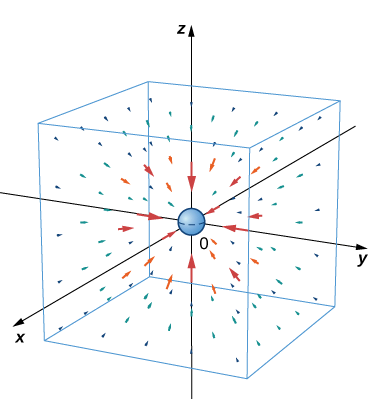
Uzito wa asteroid 1 ni kilo 750,000 na wingi wa asteroid 2 ni kilo 130,000. Fikiria asteroid 1 iko katika asili, na asteroid 2 iko\((15,−5,10)\), kipimo katika vitengo vya kilomita 10 hadi nane za nguvu. Kutokana na kwamba mara kwa mara ya mvuto wa ulimwengu wote ni\(G=6.67384×10^{−11}m^3{kg}^{−1}s^{−2}\), kupata vector nguvu ya mvuto ambayo asteroid 1 ina juu ya asteroid 2.
- Kidokezo
-
Fuata Mfano\(\PageIndex{8}\) na kwanza uhesabu umbali kati ya asteroids.
- Jibu
-
\(1.49063×{10}^{−18}\)\(4.96876×{10}^{−19}\),\(9.93752×{10}^{−19}\) N
Mashamba mazuri (Mashamba ya Kihafidhina)
Katika sehemu hii, tunasoma aina maalum ya uwanja wa vector inayoitwa shamba la gradient au shamba la kihafidhina. Mashamba haya ya vector ni muhimu sana katika fizikia kwa sababu yanaweza kutumika kutengeneza mifumo ya kimwili ambayo nishati huhifadhiwa. Mashamba ya mvuto na mashamba ya umeme yanayohusiana na malipo ya tuli ni mifano ya mashamba ya gradient.
Kumbuka kwamba kama\(f\) ni (scalar) kazi ya\(x\) na\(y\), basi gradient ya\(f\) ni
\[ \text{grad}\, f =\vecs \nabla f(x,y) =f_x(x,y) \hat{\mathbf i} +f_y(x,y) \hat{\mathbf j}. \nonumber \]
Tunaweza kuona kutoka kwa fomu ambayo gradient imeandikwa ambayo\(\vecs \nabla f\) ni shamba la vector ndani\(ℝ^2\). Vile vile, kama\(f\) ni kazi ya\(x\),\(y\), na\(z\), basi gradient ya\(f\) ni
\[ \text{grad}\, f =\vecs \nabla f(x,y,z) = f_x(x,y,z) \hat{\mathbf i}+f_y(x,y,z) \hat{\mathbf j}+f_z(x,y,z)\hat{\mathbf k}. \nonumber \]
Kipengee cha kazi ya kutofautiana tatu ni shamba la vector ndani\(ℝ^3\). shamba gradient ni uwanja vector ambayo inaweza kuandikwa kama gradient ya kazi, na tuna ufafanuzi zifuatazo.
Shamba la vector\(\vecs{F}\) ndani\(ℝ^2\) au ndani\(ℝ^3\) ni shamba la gradient ikiwa kuna kazi ya scalar\(f\) kama hiyo\(\vecs \nabla f=\vecs{F}\).
Matumizi ya teknolojia ya njama gradient vector shamba la\(f(x,y)=x^2y^2\).
Suluhisho
Gradient ya\(f\) ni\(\vecs \nabla f(x,y)=⟨2xy^2,\,2x^2y⟩\). Ili mchoro uwanja wa vector, tumia mfumo wa algebra ya kompyuta kama vile Mathematica. Kielelezo\(\PageIndex{8}\) kinaonyesha\(\vecs \nabla f\).
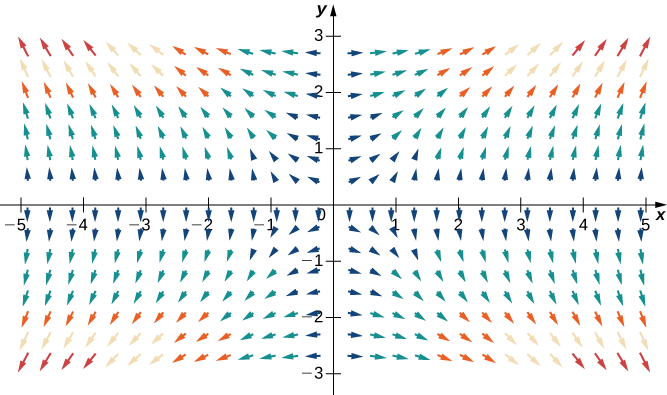
Matumizi ya teknolojia ya njama gradient vector shamba la\(f(x,y)=\sin x\cos y\).
- Kidokezo
-
Kupata gradient ya\(f\).
- Jibu
-
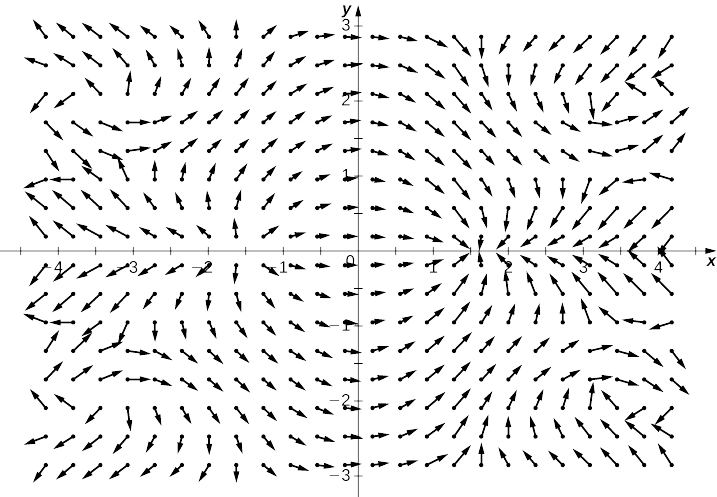
Fikiria kazi\(f(x,y)=x^2y^2\) kutoka Mfano\(\PageIndex{9}\). Kielelezo\(\PageIndex{9}\) inaonyesha curves ngazi ya kazi hii kufunikwa juu ya kazi ya gradient vector shamba. Gradient wadudu perpendicular curves ngazi, na ukubwa wa wadudu kupata kubwa kama curves ngazi kupata karibu pamoja, kwa sababu karibu makundi curves ngazi zinaonyesha grafu mwinuko, na ukubwa wa gradient vector - thamani kubwa ya derivative directional. Kwa hiyo, unaweza kuona mwinuko wa ndani wa grafu kwa kuchunguza shamba la gradient la kazi inayofanana.
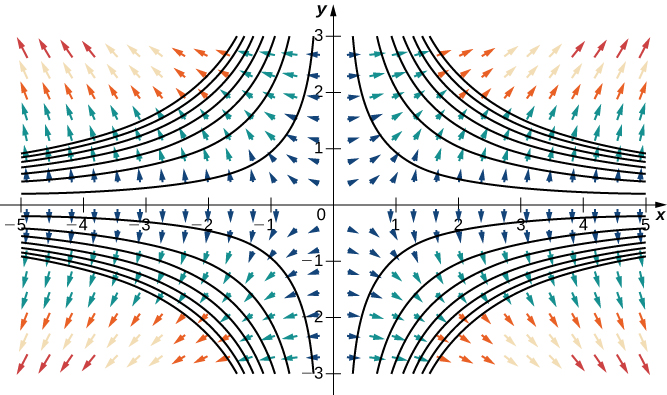
Kama tulivyojifunza mapema, uwanja wa vector\(\vecs{F}\) ni shamba la vector la kihafidhina, au shamba la gradient ikiwa kuna kazi ya scalar\(f\) kama hiyo\(\vecs \nabla f=\vecs{F}\). Katika hali hii,\(f\) inaitwa kazi ya uwezo kwa\(\vecs{F}\). Mashamba ya vector ya kihafidhina hutokea katika maombi mengi, hasa katika fizikia. Sababu mashamba hayo huitwa kihafidhina ni kwamba wao mfano wa nguvu za mifumo ya kimwili ambayo nishati huhifadhiwa. Tunasoma mashamba ya vector ya kihafidhina kwa undani zaidi baadaye katika sura hii.
Unaweza taarifa kwamba, katika baadhi ya programu, kazi uwezo\(f\) kwa\(\vecs{F}\) hufafanuliwa badala kama kazi kama hiyo\(−\vecs \nabla f=\vecs{F}\). Hii ni kesi kwa mazingira fulani katika fizikia, kwa mfano.
Ni kazi uwezo\(f(x,y,z)=x^2yz−\sin(xy)\) kwa ajili ya uwanja vector
\(\vecs{F}(x,y,z)=⟨2xyz−y\cos(xy),x^2z−x\cos(xy),x^2y⟩\)?
Suluhisho
Tunahitaji kuthibitisha kama\(\vecs \nabla f=\vecs{F}\). Tuna
\[ \begin{align*} f_x(x,y) =2xyz−y\cos(xy) \\[4pt] f_y(x,y) =x^2z−x\cos(xy) \\[4pt] f_z(x,y) =x^2y \end{align*}. \nonumber \]
Kwa hiyo,\(\vecs \nabla f=\vecs{F}\) na\(f\) ni kazi uwezo kwa ajili ya\(\vecs{F}\).
Ni kazi uwezo\(f(x,y,z)=x^2\cos(yz)+y^2z^2\) kwa ajili ya\(\vecs{F}(x,y,z)=⟨2x\cos(yz),−x^2z \sin(yz)+2yz^2,y^2⟩\)?
- Kidokezo
-
Compute gradient ya\(f\).
- Jibu
-
Hapana
Kasi ya maji inaelekezwa na shamba\(\vecs v(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\). Thibitisha kwamba\(f(x,y)=\dfrac{x^2y}{2}−\dfrac{y^2}{2}\) ni kazi uwezo kwa ajili ya\(\vecs{v}\).
Suluhisho
Kuonyesha kwamba\(f\) ni kazi uwezo, ni lazima kuonyesha kwamba\(\vecs \nabla f=\vecs v\). Kumbuka kuwa\(f_x(x,y)=xy\) na\(f_y(x,y)=\dfrac{x^2}{2}−y\). Kwa hiyo,\(\vecs \nabla f(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\) na\(f\) ni kazi uwezo kwa\(\vecs{v}\) (Kielelezo\(\PageIndex{10}\)).

Thibitisha kwamba\(f(x,y)=x^3y^2+x\) ni kazi uwezo wa shamba kasi\(\vecs{v}(x,y)=⟨3x^2y^2+1,2x^3y⟩\).
- Kidokezo
-
Tumia gradient.
- Jibu
-
\(\vecs \nabla f(x,y)=\vecs{v}(x,y)\)
Ikiwa\(\vecs{F}\) ni shamba la vector la kihafidhina, basi kuna angalau kazi moja ya uwezo\(f\) kama hiyo\(\vecs \nabla f=\vecs{F}\). Lakini, inaweza kuwa na kazi zaidi ya moja ya uwezo? Kama ni hivyo, kuna uhusiano wowote kati ya kazi mbili uwezo kwa ajili ya uwanja huo vector? Kabla ya kujibu maswali haya, hebu tukumbuke baadhi ya ukweli kutoka kwa calculus moja-variable kuongoza intuition yetu. Kumbuka kwamba ikiwa\(k(x)\) ni kazi isiyoweza kuingizwa, basi\(k\) ina antiderivatives nyingi sana. Zaidi ya hayo, kama\(\vecs{F}\) na\(\vecs{G}\) ni wote antiderivatives ya\(k\), basi\(\vecs{F}\) na\(\vecs{G}\) tofauti tu na mara kwa mara. Hiyo ni, kuna idadi fulani\(C\) kama hiyo\(\vecs{F}(x)=\vecs{G}(x)+C\).
Sasa hebu\(\vecs{F}\) kuwa kihafidhina vector shamba na basi\(f\) na\(g\) kuwa na uwezo wa kazi kwa\(\vecs{F}\). Kwa kuwa gradient ni kama derivative,\(\vecs{F}\) kuwa kihafidhina ina maana kwamba\(\vecs{F}\) ni “integrable” na “antiderivatives”\(f\) na\(g\). Kwa hiyo, kama mlinganisho na calculus moja-variable ni halali, tunatarajia kuna baadhi ya mara kwa mara\(C\) kama hiyo\(f(x)=g(x)+C\). Theorem inayofuata inasema kuwa hii ndiyo kweli.
Ili kusema theorem inayofuata kwa usahihi, tunahitaji kudhani uwanja wa uwanja wa vector umeunganishwa na kufunguliwa. Kuunganishwa ina maana ikiwa\(P_1\) na\(P_2\) ni pointi mbili katika kikoa, basi unaweza kutembea kutoka\(P_1\) kwenda\(P_2\) kwenye njia ambayo inakaa kabisa ndani ya kikoa.
Hebu\(\vecs{F}\) kuwa kihafidhina vector shamba kwenye uwanja wazi na kushikamana\(f\) na basi na\(g\) kuwa kazi kama hiyo\(\vecs \nabla f=\vecs{F}\) na\(\vecs \nabla g=\vecs{F}\). Kisha, kuna mara kwa mara\(C\) kama hiyo\(f=g+C\).
Tangu\(f\) na wote\(g\) ni kazi uwezo kwa\(\vecs{F}\), basi\(\vecs \nabla (f−g)=\vecs \nabla f−\vecs \nabla g=\vecs{F}−\vecs{F}=\vecs 0\). Hebu\(h=f−g\), basi tuna\(\vecs \nabla h=\vecs 0\) .Tungependa kuonyesha kwamba\(h\) ni kazi ya mara kwa mara.
\(h\)Kudhani ni kazi ya\(x\) na\(y\) (mantiki ya ushahidi huu inaenea kwa idadi yoyote ya vigezo huru). tangu\(\vecs \nabla h=\vecs 0\), tuna\(h_x(x,y)=0\) na\(h_y(x,y)=0\). Maneno\(h_x(x,y)=0\) yanamaanisha kuwa\(h\) ni kazi ya mara kwa mara kuhusiana na\(x\) - yaani,\(h(x,y)=k_1(y)\) kwa kazi fulani\(k_1\). Vile vile,\(h_y(x,y)=0\) ina maana\(h(x,y)=k_2(x)\) kwa kazi fulani\(k_2\). Kwa hiyo, kazi\(h\) inategemea tu\(y\) na pia inategemea tu\(x\). Hivyo,\(h(x,y)=C\) kwa baadhi ya mara kwa mara\(C\) kwenye uwanja wa kushikamana wa\(\vecs{F}\). Kumbuka kwamba sisi kweli kufanya haja ya uhusiano katika hatua hii; kama uwanja wa\(\vecs{F}\) alikuja katika vipande viwili tofauti, basi\(k\) inaweza kuwa mara kwa mara\(C_1\) juu ya kipande moja lakini inaweza kuwa mara kwa mara tofauti\(C_2\) juu ya kipande nyingine. Tangu\(f−g=h=C\), tuna hiyo\(f=g+C\), kama taka.
\(\square\)
Mashamba ya vector ya kihafidhina pia yana mali maalum inayoitwa mali ya msalaba. Mali hii husaidia kupima kama shamba la vector lililopewa ni kihafidhina.
Hebu\(\vecs{F}\) kuwa uwanja vector katika vipimo mbili au tatu kama kwamba kazi sehemu ya\(\vecs{F}\) kuwa kuendelea pili ili mchanganyiko-sehemu derivatives kwenye uwanja wa\(\vecs{F}\).
Kama\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\) ni kihafidhina vector shamba katika\(ℝ^2\), basi
\[\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}. \nonumber \]
Kama\(\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩\) ni kihafidhina vector shamba katika\({\mathbb{R}}^3\), basi
\[ \begin{align*} \dfrac{\partial P}{\partial y} =\dfrac{\partial Q}{\partial x} \\[4pt] \dfrac{\partial Q}{\partial z} =\dfrac{\partial R}{\partial y} \\[4pt] \dfrac{\partial R}{\partial x} =\dfrac{\partial P}{\partial z}. \end{align*}\]
Kwa kuwa\(\vecs{F}\) ni kihafidhina, kuna kazi\(f(x,y)\) kama hiyo\(\vecs \nabla f=\vecs{F}\). Kwa hiyo, kwa ufafanuzi wa gradient,\(f_x=P\) na\(f_y=Q\). Kwa theorem ya Clairaut,, lakini\(f_{yx}=Q_{x}\),\(f_{xy}=P_y\) na hivyo\(P_y=Q_x\).\(f_{xy}=f_{yx}\)
\(\square\)
Theorem ya Clairaut inatoa ushahidi wa haraka wa mali ya msalaba-sehemu ya mashamba ya vector kihafidhina katika\(ℝ^3\), kama ilivyokuwa kwa mashamba vector katika\(ℝ^2\).
Mali ya msalaba-sehemu ya Kihafidhina Vector Fields inaonyesha kwamba mashamba mengi ya vector si Mali ya sehemu ya msalaba ni vigumu kukidhi kwa ujumla, hivyo mashamba mengi ya vector hayatakuwa na sehemu sawa za msalaba.
Onyesha kuwa shamba la vector la mzunguko\(\vecs{F}(x,y)=⟨y,\,−x⟩\) sio kihafidhina.
Suluhisho
Hebu\(P(x,y)=y\) na\(Q(x,y)=−x\). Kama\(\vecs{F}\) ni kihafidhina, basi msalaba-partials itakuwa sawa-kwamba ni,\(P_y\) ingekuwa sawa\(Q_x\). Kwa hiyo, kuonyesha kwamba \(\vecs{F}\)si kihafidhina, kuangalia kwamba\(P_y≠Q_x\). Tangu\(P_y=1\) na\(Q_x=−1\), uwanja wa vector sio kihafidhina.
Onyesha kwamba uwanja wa vector\(\vecs F(x,y)=xy\,\hat{\mathbf i}−x^2y\,\hat{\mathbf j}\) sio kihafidhina.
- Kidokezo
-
Angalia sehemu za msalaba.
- Jibu
-
\(P_y(x,y)=x\)na\(Q_x(x,y)=−2xy\). Tangu\(P_y(x,y) ≠ Q_x(x,y)\),\(\vecs F\) si kihafidhina.
Je vector shamba\(\vecs{F}(x,y,z)=⟨7,−2,x^3⟩\) kihafidhina?
Suluhisho
Hebu\(P(x,y,z)=7\),\(Q(x,y,z)=−2\), na\(R(x,y,z)=x^3\). Ikiwa\(\vecs{F}\) ni kihafidhina, basi equations zote tatu za msalaba-sehemu zitatoshwa-yaani, ikiwa\(\vecs{F}\) ni kihafidhina, basi\(P_y\) ingekuwa sawa\(Q_x\),\(Q_z\) ingekuwa sawa\(R_y\), na\(R_x\) ingekuwa sawa\(P_z\). Kumbuka kwamba
\[P_y=Q_x=R_y=Q_z=0 \nonumber \]
hivyo kwanza mbili muhimu equalities kushikilia. Hata hivyo,\(R_x(x,y,z)=x^3\) na\(P_z(x,y,z)=0\) hivyo\(R_x≠P_z\). Kwa hiyo,\(\vecs{F}\) si kihafidhina.
Je vector shamba\(\vecs{G}(x,y,z)=⟨y,\,x,\,xyz⟩\) kihafidhina?
- Kidokezo
-
Angalia sehemu za msalaba.
- Jibu
-
Hapana
Tunahitimisha sehemu hii kwa neno la onyo: Mali ya Msalaba wa Mashamba ya Vector ya Conservative Vector anasema kuwa ikiwa\(\vecs{F}\) ni kihafidhina, basi\(\vecs{F}\) ina mali ya msalaba-sehemu. Theorem haina kusema kwamba, ikiwa\(\vecs{F}\) ina mali ya msalaba-sehemu, basi\(\vecs{F}\) ni kihafidhina (kuzungumza kwa maana sio sawa na maana ya awali). Kwa maneno mengine, Mali ya Msalaba wa Mashamba ya Vector ya Kihafidhina yanaweza kusaidia tu kuamua kwamba shamba sio kihafidhina; haukuruhusu kuhitimisha kuwa shamba la vector ni kihafidhina.
Kwa mfano, fikiria uwanja wa vector\(\vecs{F}(x,y)=⟨x^2y,\dfrac{x^3}{3}⟩\). Shamba hili lina mali ya msalaba-sehemu, hivyo ni kawaida kujaribu kutumia Mali ya Msalaba wa Mashamba ya Vector ya Conservative ili kuhitimisha uwanja huu wa vector ni kihafidhina. Hata hivyo, hii ni matumizi mabaya ya theorem. Tunajifunza baadaye jinsi ya kuhitimisha kuwa\(\vecs F\) ni kihafidhina.
Dhana muhimu
- uwanja vector inateua vector\(\vecs{F}(x,y)\) kwa kila hatua\((x,y)\) katika subset\(D\) ya\(ℝ^2\) au\(ℝ^3\). \(\vecs{F}(x,y,z)\)kwa kila hatua\((x,y,z)\) katika subset\(D\) ya\(ℝ^3\).
- Mashamba ya vector yanaweza kuelezea usambazaji wa wingi wa vector kama vile vikosi au kasi juu ya eneo la ndege au la nafasi. Wao ni matumizi ya kawaida katika maeneo kama vile fizikia, uhandisi, hali ya hewa, oceanography.
- Tunaweza mchoro shamba vector kwa kuchunguza equation yake kufafanua kuamua magnitudes jamaa katika maeneo mbalimbali na kisha kuchora wadudu kutosha kuamua mfano.
- Shamba la vector\(\vecs{F}\) linaitwa kihafidhina ikiwa kuna kazi ya scalar\(f\) kama hiyo\(\vecs \nabla f=\vecs{F}\).
Mlinganyo muhimu
- Vector shamba katika\(ℝ^2\)
\(\vecs{F}(x,y)=⟨P(x,y),\,Q(x,y)⟩\)
au
\(\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}\) - Vector shamba katika\(ℝ^3\)
\(\vecs{F}(x,y,z)=⟨P(x,y,z),\,Q(x,y,z),\,R(x,y,z)⟩\)
au
\(\vecs{F}(x,y,z)=P(x,y,z) \,\hat{\mathbf i} +Q(x,y,z) \,\hat{\mathbf j}+R(x,y,z) \,\hat{\mathbf k}\)
faharasa
- uwanja wa kihafidhina
- shamba la vector ambalo lipo kazi ya scalar\(f\) kama hiyo\(\vecs ∇f=\vecs{F}\)
- uwanja wa gradient
- uwanja wa vector ambayo kuna kazi ya scalar\(f\) kama hiyo\(\vecs ∇f=\vecs{F}\);\(\vecs{F}\) kwa maneno mengine, uwanja wa vector ambayo ni gradient ya kazi; mashamba hayo ya vector pia huitwa kihafidhina
- kazi inayoweza
- kazi ya scalar\(f\) kama hiyo\(\vecs ∇f=\vecs{F}\)
- uwanja wa radial
- shamba la vector ambalo vectors zote zinaelekeza moja kwa moja kuelekea au moja kwa moja mbali na asili; ukubwa wa vector yoyote inategemea tu umbali wake kutoka kwa asili
- uwanja wa mzunguko
- uwanja wa vector ambayo vector katika hatua\((x,y)\) ni tangent kwa mduara na radius\(r=\sqrt{x^2+y^2}\); katika uwanja wa mzunguko, wadudu wote hutoka ama saa moja kwa moja au kinyume chake, na ukubwa wa vector inategemea tu umbali wake kutoka kwa asili
- kitengo vector shamba
- shamba la vector ambalo ukubwa wa kila vector ni 1
- uwanja wa vector
- kipimo katika\(ℝ^2\), kazi ya vector\(\vecs{F}(x,y)\) kwa kila hatua\((x,y)\) ya subset\(D\) ya\(ℝ^2\); katika\(ℝ^3\), kazi ya vector\(\vecs{F}(x,y,z)\) kwa kila hatua\((x,y,z)\) ya subset\(D\) ya\(ℝ^3\)


