13.1: Kazi za Vector-Thamani na Curves za Nafasi
- Page ID
- 178295
- Andika equation ya jumla ya kazi yenye thamani ya vector katika fomu ya sehemu na fomu ya kitengo-vector.
- Kutambua equations parametric kwa Curve nafasi.
- Eleza umbo la helix na uandike equation yake.
- Eleza kikomo cha kazi yenye thamani ya vector.
Utafiti wetu wa kazi za thamani ya vector unachanganya mawazo kutoka kwa uchunguzi wetu wa awali wa calculus moja-variable na maelezo yetu ya vectors katika vipimo vitatu kutoka sura iliyotangulia. Katika sehemu hii, tunapanua dhana kutoka kwa sura za awali na pia kuchunguza mawazo mapya kuhusu curves katika nafasi tatu-dimensional. Ufafanuzi huu na theorems husaidia uwasilishaji wa nyenzo katika sura hii yote na pia katika sura zilizobaki za maandiko.
Ufafanuzi wa Kazi ya Vector-Thamani
Hatua yetu ya kwanza katika kusoma hesabu ya kazi za thamani ya vector ni kufafanua nini hasa kazi ya thamani ya vector ni. Tunaweza kisha kuangalia grafu ya kazi vector thamani na kuona jinsi wao kufafanua curves katika vipimo mbili na tatu.
Kazi yenye thamani ya vector ni kazi ya fomu
\[\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \; \; \text{or} \; \;\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}+h(t)\,\hat{\mathbf{k}}, \nonumber \]
ambapo kazi ya sehemu\(f\),, na\(g\)\(h\), ni kazi halisi ya thamani ya parameter\(t\). Kazi yenye thamani ya Vector pia imeandikwa kwa fomu
\[\vecs r(t)=⟨f(t),\,g(t)⟩ \; \; \text{or} \; \; \vecs r(t)=⟨f(t),\,g(t),\,h(t)⟩. \nonumber \]
Katika matukio hayo yote, fomu ya kwanza ya kazi inafafanua kazi ya thamani ya vector mbili-dimensional; fomu ya pili inaelezea kazi ya thamani ya vector tatu-dimensional.
Kipimo\(t\) kinaweza kulala kati ya namba mbili halisi:\(a≤t≤b\). Uwezekano mwingine ni kwamba thamani ya\(t\) inaweza kuchukua namba zote halisi. Mwisho, sehemu kazi wenyewe inaweza kuwa na vikwazo uwanja kwamba kutekeleza vikwazo juu ya thamani ya\(t\). Mara nyingi tunatumia\(t\) kama parameter kwa sababu\(t\) inaweza kuwakilisha wakati.
Kwa kila moja ya kazi zifuatazo za thamani ya vector, tathmini\(\vecs r(0)\),\(\vecs r(\frac{\pi}{2})\), na\(\vecs r(\frac{2\pi}{3})\). Je! Yoyote ya kazi hizi ina vikwazo vya kikoa?
- \(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}\)
- \(\vecs r(t)=3\tan t\,\hat{\mathbf{i}}+4 \sec t\,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}}\)
Suluhisho
- Ili kuhesabu kila moja ya maadili ya kazi, badala ya thamani sahihi ya\(t\) ndani ya kazi:
\ kuanza {\ mangano*}\ vecs r (0)\; = 4\ cos (0)\ kofia {\ mathbf {i}} +3\ sin (0)\ kofia {\ mathbf {j}}\ [4pt] =4\ kofia {\ mathbf {i}} +0\ hath {\ mathbf {j} =4\ kofia {\ mathbf {\ hath {\ mathbf {j} bf {i}\\ [4pt]\ vecs r\ kushoto (\ frac {\ pi} {2}\ haki)\; = 4\ cos\ kushoto (\ frac {π} {2}\ haki)\ kofia {\ mathbf {i}} +3\ dhambi\ kushoto (\ frac {π} {2}\ haki)\ kofia {\ mathbf {j}}\\ [4pt] = 0\ kofia {\ mathbf {i}} + 3\ kofia {\ mathbf {j}} =3\ kofia {\ mathbf {j}}\\ [4pt]\ vecs r\ kushoto (\ frac {2\ pi} {3}\ haki)\; =4\ cos\ kushoto (\ frac {2π} {3}\ haki)\ kofia {\ mathbf {i}} +3\ sin\ kushoto (\ frac {2π} {3}\ haki)\ kofia {\ mathbf {j}}\\ [4pt] =4\ kushoto (合\ tfrac {1} {2}\ haki)\ kofia {\ mathbf {i}} +3\ kushoto (\ tfrac {\ sqrt {3}} {2}\ haki)\ kofia {\ mathbf j {}} =18-2\ kofia {\ mathbf {i}} +\ tfrac {3\ sqrt {3}} {2}\ kofia {\ mathbf {j}}\ mwisho {align*}
Kuamua kama kazi hii ina vikwazo vyovyote vya kikoa, fikiria kazi za sehemu tofauti. Kazi ya kwanza ya sehemu ni\(f(t)=4 \cos t\) na kazi ya pili ya sehemu ni\(g(t)=3\sin t\). Wala wa kazi hizi ina kizuizi cha kikoa, hivyo uwanja wa\(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\) ni namba zote halisi. - Ili kuhesabu kila moja ya maadili ya kazi, badala ya thamani sahihi ya t katika kazi:\[\begin{align*}\vecs r(0) \; = 3\tan(0)\hat{\mathbf{i}}+4\sec(0) \hat{\mathbf{j}}+5(0) \hat{\mathbf{k}} \\[4pt] = 0\hat{\mathbf{i}}+4j+0 \hat{\mathbf{k}}=4 \hat{\mathbf{j}} \\[4pt] \vecs r\left(\frac{\pi}{2}\right) \; = 3\tan\left(\frac{\pi}{2}\right)\hat{\mathbf{i}}+4\sec\left(\frac{\pi}{2}\right) \hat{\mathbf{j}}+5\left(\frac{\pi}{2}\right) \hat{\mathbf{k}},\,\text{which does not exist} \\[4pt] \vecs r\left(\frac{2\pi}{3}\right) \; =3\tan\left(\frac{2 \pi}{3}\right)\hat{\mathbf{i}}+4\sec\left(\frac{2\pi}{3}\right) \hat{\mathbf{j}}+5\left(\frac{2\pi}{ 3}\right) \hat{\mathbf{k}} \\[4pt] =3(−\sqrt{3})\hat{\mathbf{i}}+4(−2)\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}} \\[4pt] =(-3\sqrt{3})\hat{\mathbf{i}}−8\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}}\end{align*}\] Kuamua kama kazi hii ina vikwazo vya kikoa chochote, fikiria kazi za sehemu tofauti. Kazi ya kwanza ya sehemu ni\(f(t)=3\tan t\), kazi ya pili ya sehemu ni\(g(t)=4\sec t\), na kazi ya sehemu ya tatu ni\(h(t)=5t\). kwanza kazi mbili si defined kwa mafungu isiyo ya kawaida ya\(\frac{\pi}{2}\), hivyo kazi si defined kwa mafungu isiyo ya kawaida ya\(\frac{\pi}{2}\). Kwa hiyo,\[\text{D}_{\vecs r}=\Big\{t\,|\,t≠ \frac{(2n+1)\pi}{2}\Big\},\nonumber \]\(n\) wapi integer yoyote.
Kwa kazi yenye thamani ya vector\(\vecs r(t)=(t^2−3t) \,\hat{\mathbf{i}}+(4t+1) \,\hat{\mathbf{j}}\), tathmini\(\vecs r(0),\, \vecs r(1)\), na\(\vecs r(−4)\). Je! Kazi hii ina vikwazo vya kikoa?
- Kidokezo
-
Badilisha maadili sahihi ya\(t\) ndani ya kazi.
- Jibu
-
\(\vecs r(0) = \hat{\mathbf{j}},\, \vecs r(1)=−2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}},\, \vecs r(−4)=28 \hat{\mathbf{i}}−15 \hat{\mathbf{j}}\)
uwanja wa\(\vecs r(t)=(t^2−3t)\hat{\mathbf{i}}+(4t+1)\hat{\mathbf{j}}\) ni namba zote halisi.
Mfano\(\PageIndex{1}\) unaeleza dhana muhimu. Kikoa cha kazi yenye thamani ya vector lina idadi halisi. Domain inaweza kuwa namba zote halisi au subset ya idadi halisi. Kazi mbalimbali ya thamani ya vector ina vectors. Kila namba halisi katika uwanja wa kazi yenye thamani ya vector imewekwa kwa vector mbili au tatu-dimensional vector.
Graphing Vector-Thamani Kazi
Kumbuka kwamba vector ndege ina kiasi mbili: mwelekeo na ukubwa. Kutokana na hatua yoyote katika ndege (hatua ya awali), ikiwa tunahamia mwelekeo maalum kwa umbali maalum, tunawasili hatua ya pili. Hii inawakilisha hatua ya mwisho ya vector. Tunahesabu vipengele vya vector kwa kuondoa kuratibu za hatua ya awali kutoka kwa kuratibu za hatua ya mwisho.
Vector inachukuliwa kuwa katika nafasi ya kawaida ikiwa hatua ya awali iko katika asili. Wakati graphing kazi vector-thamani, sisi kawaida grafu wadudu katika uwanja wa kazi katika nafasi ya kawaida, kwa sababu kufanya hivyo dhamana ya pekee ya grafu. Mkataba huu unatumika kwa grafu ya kazi tatu-dimensional vector-thamani pia. Grafu ya kazi ya thamani ya vector ya fomu
\[\vecs r(t)=f(t)\, \hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \nonumber \]
lina seti ya pointi zote\((f(t),\,g(t))\), na njia ya athari inaitwa Curve ndege. Grafu ya kazi ya thamani ya vector ya fomu
\[\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}} \nonumber \]
lina seti ya pointi zote\((f(t),\,g(t),\,h(t))\), na njia ya athari inaitwa Curve nafasi. Uwakilishi wowote wa safu ya ndege au safu ya nafasi kwa kutumia kazi yenye thamani ya vector inaitwa parameterization ya vector ya curve.
Kila Curve ndege na nafasi Curve ina mwelekeo, unahitajika kwa mishale inayotolewa katika juu ya Curve, ambayo inaonyesha mwelekeo wa mwendo pamoja Curve kama thamani ya parameter\(t\) kuongezeka.
Unda grafu ya kila moja ya kazi zifuatazo za thamani ya vector:
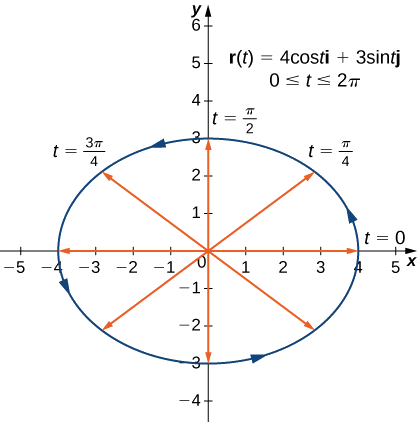
- Curve ndege inawakilishwa na\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\),\(0≤t≤2\pi\)
- Curve ndege inawakilishwa na\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\)
- Curve nafasi inawakilishwa na\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\),\(0≤t≤4\pi\)
Suluhisho
1. Kama ilivyo na grafu yoyote, tunaanza na meza ya maadili. Sisi kisha grafu kila vectors katika safu ya pili ya meza katika nafasi ya kawaida na kuunganisha pointi terminal ya kila vector kuunda Curve (Kielelezo\(\PageIndex{1}\)). Curve hii inageuka kuwa duaradufu unaozingatia asili.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)” style="wima align:katikati; ">\(0\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(4\hat{\mathbf{i}}\) | \ (t\)” style="wima align:katikati; ">\(\pi\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(-4\hat{\mathbf{i}}\) |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t\)” style="wima align:katikati; ">\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(-2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{\pi}{2}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t\)” style="wima align:katikati; ">\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\( -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t\)” style="wima align:katikati; ">\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\( 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t\)” style="wima align:katikati; ">\(2\pi\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(4\hat{\mathbf{i}}\) | \ (t\)” style="wima align:katikati; "> | \ (\ vecs r (t)\)” style="wima align:katikati; "> |
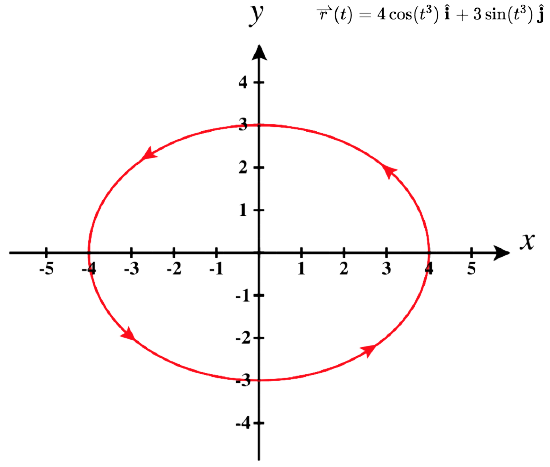
2. Jedwali la maadili kwa\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\) ni kama ifuatavyo:
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)” style="wima align:katikati; ">\(0\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)” style="wima align:katikati; ">\(\displaystyle\sqrt[3]{\pi}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{-4\hat{\mathbf{i}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\displaystyle \sqrt[3]{\dfrac{\pi}{4}}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t\)” style="wima align:katikati; ">\(\displaystyle \sqrt[3]{\dfrac{5\pi}{4}}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\displaystyle \sqrt[3]{\dfrac{\pi}{2}}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t\)” style="wima align:katikati; ">\(\displaystyle \sqrt[3]{\dfrac{3\pi}{2}}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\displaystyle \sqrt[3]{\dfrac{3\pi}{4}}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t\)” style="wima align:katikati; ">\(\displaystyle \sqrt[3]{\dfrac{7\pi}{4}}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t\)” style="wima align:katikati; ">\( \displaystyle\sqrt[3]{2\pi}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)” style="wima align:katikati; "> | \ (\ vecs r (t)\)” style="wima align:katikati; "> |
Grafu ya curve hii pia ni ellipse iliyozingatia asili.
3. Tunapitia utaratibu huo kwa kazi ya vector tatu-dimensional.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)” style="wima align:katikati; ">\(\mathrm{0}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)” style="wima align:katikati; ">\(\mathrm{\pi}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{-4\hat{\mathbf{i}}}+ \pi \hat{\mathbf{k}}\) |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{\pi}{4} \hat{\mathbf{k}}}\) | \ (t\)” style="wima align:katikati; ">\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{5\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{\pi}{2}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{4\hat{\mathbf{j}} +\frac{\pi}{2} \hat{\mathbf{k}}}\) | \ (t\)” style="wima align:katikati; ">\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{-4\hat{\mathbf{j}} +\frac{3\pi}{2} \hat{\mathbf{k}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{3\pi}{4} \hat{\mathbf{k}}}\) | \ (t\)” style="wima align:katikati; ">\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{7\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t\)” style="wima align:katikati; ">\(\mathrm{2\pi}\) | \ (\ vecs r (t)\)” style="wima align:katikati; ">\(\mathrm{4\hat{\mathbf{j}} + 2\pi \hat{\mathbf{k}}}\) | \ (t\)” style="wima align:katikati; "> | \ (\ vecs r (t)\)” style="wima align:katikati; "> |
Maadili kisha kurudia wenyewe, isipokuwa kwa ukweli kwamba mgawo wa daima\(\hat{\mathbf{k}}\) unaongezeka (\(\PageIndex{3}\)). Curve hii inaitwa helix. Angalia kwamba ikiwa\(\hat{\mathbf{k}}\) sehemu hiyo imeondolewa, basi kazi inakuwa\(\vecs r(t)=4\cos t \hat{\mathbf{i}}+ 4\sin t \hat{\mathbf{j}}\), ambayo ni mduara wa radius 4 unaozingatia asili.

Unaweza kuona kwamba grafu katika sehemu a. na b. ni sawa. Hii hutokea kwa sababu kazi kuelezea Curve b ni kinachojulikana reparameterization ya kazi kuelezea Curve a. kwa kweli, Curve yoyote ina idadi usio wa reparameterizations; kwa mfano, tunaweza kuchukua nafasi\(t\) na\(2t\) katika yoyote ya curves tatu uliopita bila kubadilisha sura ya curve. Muda juu ya ambayo\(t\) hufafanuliwa inaweza kubadilika, lakini hiyo ndiyo yote. Tunarudi kwenye wazo hili baadaye katika sura hii tunapojifunza parameterization ya urefu wa arc. Kama ilivyoelezwa, jina la sura ya pembe ya grafu ndani\(\PageIndex{3}\) ni helix. Curve inafanana na chemchemi, na sehemu ya mviringo inayoangalia chini kando ya\(z\) -axis. Inawezekana kwa helix kuwa elliptical katika sehemu ya msalaba pia. Kwa mfano, kazi yenye thamani ya vector\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) inaelezea helix elliptical. Makadirio ya helix hii ndani ya\(xy\) -ndege ni duaradufu. Mwisho, mishale katika grafu ya helix hii inaonyesha mwelekeo wa curve kama\(t\) inavyoendelea kutoka\(0\) hadi\(4π\).
Unda grafu ya kazi yenye thamani ya vector\(\vecs r(t)=(t^2−1)\hat{\mathbf{i}}+(2t−3) \hat{\mathbf{j}}\),\(0≤t≤3\).
- Kidokezo
-
Anza kwa kufanya meza ya maadili, kisha graph vectors kwa kila thamani ya\(t\).
- Jibu
-
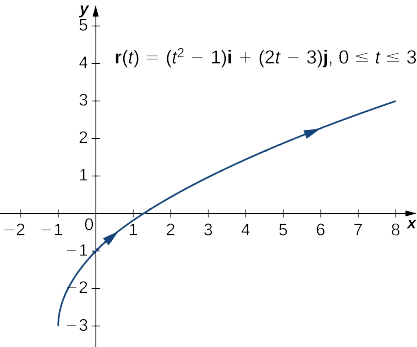
Kwa hatua hii, unaweza kuona kufanana kati ya kazi za thamani ya vector na curves parameterized. Hakika, kutokana na kazi yenye thamani ya vector\(\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}\) tunaweza kufafanua\(x=f(t)\) na\(y=g(t)\). Ikiwa kizuizi kipo kwenye maadili ya\(t\) (kwa mfano,\(t\) ni vikwazo kwa muda\([a,b]\) kwa vipindi vingine\(a<b\), basi kizuizi hiki kinatekelezwa kwenye parameter. Grafu ya kazi ya parameterized ingekubaliana na grafu ya kazi yenye thamani ya vector, isipokuwa kwamba grafu yenye thamani ya vector ingewakilisha vectors badala ya pointi. Kwa kuwa tunaweza parameterize Curve inavyoelezwa na kazi\(y=f(x)\), inawezekana pia kuwakilisha holela ndege Curve na kazi vector-thamani.
Mipaka na Kuendelea kwa Kazi ya Vector-Thamani
Sasa tunaangalia kikomo cha kazi yenye thamani ya vector. Hii ni muhimu kuelewa kujifunza hesabu ya kazi za thamani ya vector.
Kazi yenye thamani ya vector\(\vecs r\) inakaribia kikomo\(\vecs L\) kama\(t\) mbinu\(a\), imeandikwa
\[\lim \limits_{t \to a} \vecs r(t) = \vecs L, \nonumber \]
kuandaliwa
\[\lim \limits_{t \to a} \big\| \vecs r(t) - \vecs L \big\| = 0. \nonumber \]
Hii ni ufafanuzi mkali wa kikomo cha kazi yenye thamani ya vector. Katika mazoezi, tunatumia theorem ifuatayo:
Hebu\(f\),\(g\), na\(h\) uwe na kazi za\(t\). Kisha kikomo cha kazi yenye thamani ya vector\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) kama t inakaribia kama hutolewa na
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} , \label{Th1} \]
zinazotolewa mipaka\(\lim \limits_{t \to a} f(t)\) na\(\lim \limits_{t \to a} g(t)\) kuwepo.
Vile vile, kikomo cha kazi yenye thamani ya vector\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) kama\(t\) mbinu\(a\) hutolewa na
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} +[\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}} , \label{Th2} \]
zinazotolewa mipaka\(\lim \limits_{t \to a} f(t)\),\(\lim \limits_{t \to a} g(t)\) na\(\lim \limits_{t \to a} h(t)\) zipo.
Katika mfano unaofuata, tunaonyesha jinsi ya kuhesabu kikomo cha kazi yenye thamani ya vector.
Kwa kila moja ya kazi zifuatazo za thamani ya vector, tumia\(\lim \limits_{t \to 3}\vecs r(t)\) mahesabu
- \(\vecs r(t)=(t^2−3t+4) \hat{\mathbf{i}}+(4t+3)\hat{\mathbf{j}}\)
- \(\vecs r(t)=\frac{2t−4}{t+1}\hat{\mathbf{i}}+\frac{t}{t^2+1} \hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\)
Suluhisho
- Tumia Equation\ ref {Th1} na\(t=3\) ubadilishe thamani katika maneno mawili ya sehemu:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3} \left[(t^2−3t+4) \hat{\mathbf{i}} + (4t+3) \hat{\mathbf{j}}\right] \\[4pt] = \left[\lim \limits_{t \to 3} (t^2−3t+4)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} (4t+3)\right] \hat{\mathbf{j}} \\[4pt] = 4 \hat{\mathbf{i}}+15 \hat{\mathbf{j}} \end{align*}\]
- Tumia Equation\ ref {Th2} na ubadilishe thamani\(t=3\) katika maneno matatu ya sehemu:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3}\left(\dfrac{2t−4}{t+1}\hat{\mathbf{i}}+\dfrac{t}{t^2+1}\hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\right) \\[4pt] = \left[\lim \limits_{t \to 3} \left(\dfrac{2t−4}{t+1}\right)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} \left(\dfrac{t}{t^2+1}\right)\right] \hat{\mathbf{j}} +\left[\lim \limits_{t \to 3} (4t−3)\right] \hat{\mathbf{k}} \\[4pt] = \tfrac{1}{2} \hat{\mathbf{i}}+\tfrac{3}{10}\hat{\mathbf{j}}+9 \hat{\mathbf{k}} \end{align*}\]
\(\lim \limits_{t \to 2} \vecs r(t)\)Tumia kazi\(\vecs r(t) = \sqrt{t^2 + 3t - 1}\,\hat{\mathbf{i}}−(4t-3)\hat{\mathbf{j}}− \sin \frac{(t+1)\pi}{2}\hat{\mathbf{k}}\)
- Kidokezo
-
Tumia Equation\ ref {Th2} kutoka theorem iliyotangulia.
- Jibu
-
\[\lim \limits_{t \to 2} \vecs r(t) = 3\hat{\mathbf{i}}−5\hat{\mathbf{j}}+\hat{\mathbf{k}} \nonumber \]
Sasa kwa kuwa tunajua jinsi ya kuhesabu kikomo cha kazi yenye thamani ya vector, tunaweza kufafanua kuendelea kwa hatua kwa kazi hiyo.
Hebu\(f\),\(g\), na\(h\) uwe na kazi za\(t\). Kisha, kazi yenye thamani ya vector\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) inaendelea kwa uhakika\(t=a\) ikiwa hali tatu zifuatazo zinashikilia:
- \(\vecs r(a)\)ipo
- \(\lim \limits_{t \to a} \vecs r(t)\)ipo
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Vile vile, kazi yenye thamani ya vector\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) inaendelea kwa uhakika\(t=a\) ikiwa hali tatu zifuatazo zinashikilia:
- \(\vecs r(a)\)ipo
- \(\lim \limits_{t \to a} \vecs r(t)\)ipo
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Muhtasari
- Kazi yenye thamani ya vector ni kazi ya fomu\(\vecs r(t)=f(t) \hat{\mathbf{i}}+ g(t) \hat{\mathbf{j}}\) au\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), ambapo sehemu inafanya kazi\(f\),\(g\), na\(h\) ni kazi halisi ya parameter\(t\).
- Grafu ya kazi ya thamani ya vector ya fomu\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) inaitwa curve ya ndege. Grafu ya kazi ya thamani ya vector ya fomu\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) inaitwa safu ya nafasi.
- Inawezekana kuwakilisha curve ya ndege ya kiholela na kazi yenye thamani ya vector.
- Ili kuhesabu kikomo cha kazi yenye thamani ya vector, uhesabu mipaka ya kazi za sehemu tofauti.
Mlinganyo muhimu
- Vector yenye thamani ya kazi
\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) au\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\),\(\vecs r(t)=⟨f(t),g(t)⟩\) au\(\vecs r(t)=⟨f(t),g(t),h(t)⟩\) - Kikomo cha kazi yenye thamani ya
\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}}\) vector au\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} + [\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}}\)
faharasa
- kazi za sehemu
- kazi ya sehemu ya kazi ya thamani ya vector\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) ni\(f(t)\) na\(g(t)\), na kazi ya sehemu ya kazi ya thamani ya vector\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) ni\(f(t)\),\(g(t)\) na\(h(t)\)
- helix
- curve tatu-dimensional katika sura ya ond
- kikomo cha kazi yenye thamani ya vector
- kazi yenye thamani ya vector\(\vecs r(t)\) ina kikomo\(\vecs L\) kama\(t\) mbinu\(a\) kama\(\lim \limits{t \to a} \left| \vecs r(t) - \vecs L \right| = 0\)
- ndege Curve
- seti ya jozi zilizoamriwa\((f(t),g(t))\) pamoja na usawa wao wa parametric\(x=f(t)\) na\(y=g(t)\)
- parameterization
- parameterization mbadala ya kazi iliyotolewa yenye thamani ya vector
- nafasi Curve
- seti ya triples kuamuru\((f(t),g(t),h(t))\) pamoja na wao kufafanua equations parametric\(x=f(t)\),\(y=g(t)\) na\(z=h(t)\)
- parameterization vector
- uwakilishi wowote wa ndege au nafasi Curve kwa kutumia kazi yenye thamani ya vector
- kazi yenye thamani ya vector
- kazi ya fomu\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) au\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\), ambapo kazi ya sehemu\(f\),\(g\), na\(h\) ni kazi halisi ya thamani ya parameter\(t\).
Wachangiaji na Majina
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College)


