12.6: Nyuso za Quadric

Last updated
Save as PDF

Page ID: 178159

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tambua silinda kama aina ya uso wa tatu-dimensional.
Tambua sifa kuu za ellipsoids, paraboloids, na hyperboloids.
Tumia maelekezo ya kuteka makutano ya nyuso za quadric na ndege za kuratibu.

Tumekuwa tukichunguza vectors na shughuli za vector katika nafasi tatu-dimensional, na tumeanzisha equations kuelezea mistari, ndege, na nyanja. Katika sehemu hii, tunatumia ujuzi wetu wa ndege na nyanja, ambazo ni mifano ya takwimu tatu-dimensional inayoitwa nyuso, kuchunguza aina mbalimbali za nyuso nyingine ambazo zinaweza kupigwa katika mfumo wa kuratibu tatu-dimensional.

Kutambua mitungi

Uso wa kwanza tutaweza kuchunguza ni silinda. Ingawa watu wengi mara moja wanafikiria bomba la mashimo au majani ya soda wanaposikia neno silinda, hapa tunatumia maana pana ya hisabati ya neno. Kama tulivyoona, nyuso za cylindrical hazipaswi kuwa mviringo. Duct inapokanzwa mstatili ni silinda, kama vile kitanda cha yoga kilichopandwa, sehemu ya msalaba ambayo ni sura ya ond.

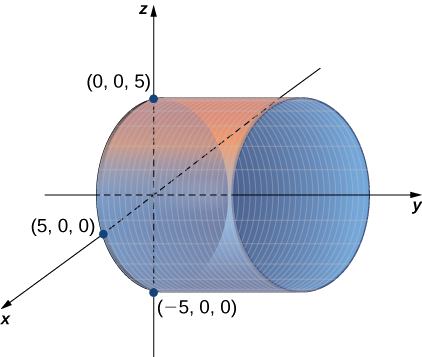
Katika ndege ya kuratibu mbili-dimensional, equation$ x^2+y^2=9$ inaelezea mduara unaozingatia asili na radius$ 3$. Katika nafasi tatu-dimensional, equation hii sawa inawakilisha uso. Fikiria nakala za mduara uliowekwa juu ya kila mmoja unaozingatia$z$ -axis (Kielelezo$\PageIndex{1}$), na kutengeneza tube ya mashimo. Tunaweza kisha kujenga silinda kutoka seti ya mistari sambamba na$z$ -axis kupita kupitia mduara$ x^2+y^2=9$ katika$xy$ -ndege, kama inavyoonekana katika takwimu. Kwa njia hii, safu yoyote katika moja ya ndege za kuratibu inaweza kupanuliwa kuwa uso.

Takwimu hii mfumo wa kuratibu 3-dimensional. Ina kituo cha mviringo cha kulia na mhimili wa z kupitia kituo. Silinda pia ina pointi zilizoandikwa kwenye mhimili x na y katika (3, 0, 0) na (0, 3, 0). — Kielelezo$\PageIndex{1}$: Katika nafasi tatu-dimensional, grafu ya equation$ x^2+y^2=9$ ni silinda na radius$ 3$ iliyozingatia$z$ -axis. Inaendelea kwa muda usiojulikana katika maelekezo mazuri na mabaya.

Ufafanuzi: mitungi na maamuzi

Seti ya mistari inayofanana na mstari uliotolewa unaopita kupitia pembe iliyotolewa inajulikana kama uso wa cylindrical, au silinda. Mstari sambamba huitwa maamuzi.

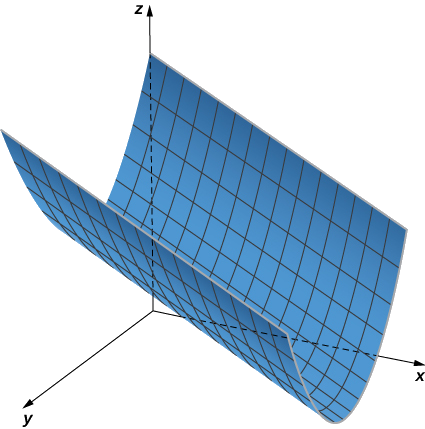
Kutokana na ufafanuzi huu, tunaweza kuona kwamba bado tuna silinda katika nafasi tatu-dimensional, hata kama Curve si mduara. Curve yoyote inaweza kuunda silinda, na maamuzi ambayo hutunga silinda inaweza kuwa sawa na mstari wowote (Kielelezo$\PageIndex{2}$).

Takwimu hii ina uso wa 3-dimensional unaoanza kwenye mhimili wa y na hupanda juu. Pia kuna x na z axes iliyoandikwa. — Kielelezo$\PageIndex{2}$: Katika nafasi tatu-dimensional, grafu ya equation$ z=x^3$ ni silinda, au uso cylindrical na maamuzi sambamba na$y$ -axis.

Mfano$ \PageIndex{1}$: Graphing Cylindrical Surfaces

Mchoro grafu ya nyuso zifuatazo za cylindrical.

$ x^2+z^2=25$
$ z=2x^2−y$
$ y=\sin x$

Suluhisho

a. variable$ y$ inaweza kuchukua thamani yoyote bila kikomo. Kwa hiyo, mistari inayoongoza uso huu ni sawa na$y$ -axis. Mfululizo wa uso huu na$xz$ -ndege huunda mduara unaozingatia asili na radius$ 5$ (angalia Mchoro$\PageIndex{3}$).

Takwimu hii ni mfumo wa kuratibu wa 3-dimensional. Ina silinda ya mviringo ya kulia upande wake na mhimili wa y katikati. Silinda inakabiliana na x-axis saa (5, 0, 0). Pia ina pointi mbili za makutano iliyoandikwa kwenye mhimili wa z (0, 0, 5) na (0, 0, -5). — Kielelezo$\PageIndex{3}$: Grafu ya equation$ x^2+z^2=25$ ni silinda na radius$ 5$ unaozingatia$y$ -axis.

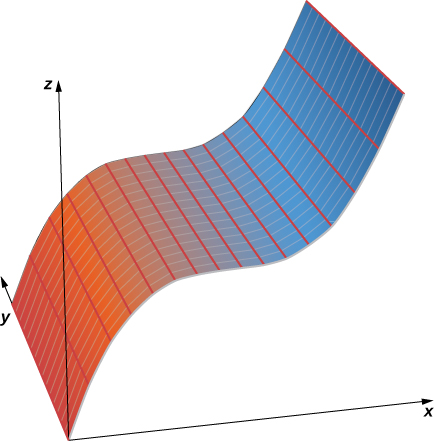
b Katika kesi hii, equation ina vigezo vyote vitatu -$ x,y,$ na$ z$ - hivyo hakuna hata moja ya vigezo inaweza kutofautiana kiholela. Njia rahisi zaidi ya kutazama uso huu ni kutumia matumizi ya kompyuta ya graphing (Kielelezo$\PageIndex{4}$).

Takwimu hii ina uso katika octant ya kwanza. Sehemu ya msalaba wa imara ni parabola. — Kielelezo$\PageIndex{4}$

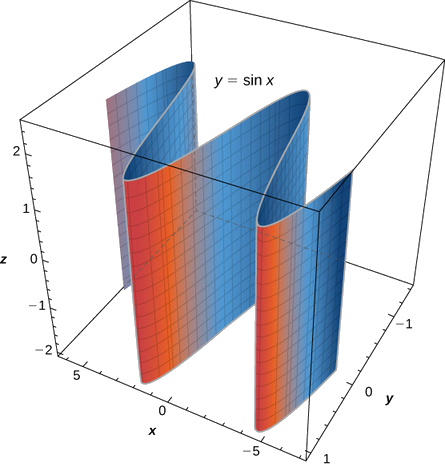
c Katika equation hii, variable$ z$ inaweza kuchukua thamani yoyote bila kikomo. Kwa hiyo, mistari inayojumuisha uso huu ni sawa na$z$ -axis. Mfululizo wa uso huu na xy -plane inaelezea Curve$ y=\sin x$ (Kielelezo$\PageIndex{5}$).

Takwimu hii ni uso wa tatu wa mwelekeo. sehemu ya msalaba wa uso sambamba na x y ndege itakuwa sine Curve. — Kielelezo$\PageIndex{5}$: Grafu ya equation$ y=\sin x$ inaundwa na seti ya mistari sambamba na$z$ -axis kupita kwa njia ya curve$ y=\sin x$ katika$xy$ -plane.

Zoezi$ \PageIndex{1}$:

Mchoro au kutumia chombo graphing kuona grafu ya uso cylindrical inavyoelezwa na equation$ z=y^2$.

Kidokezo: Variable$ x$ inaweza kuchukua thamani yoyote bila kikomo.
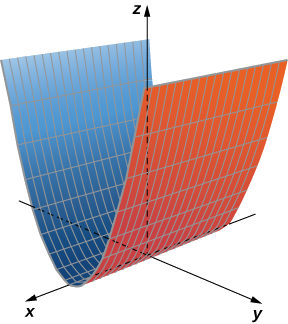
Jibu: $Takwimu hii ni uso juu ya ndege ya x y. Sehemu ya msalaba wa uso huu sambamba na ndege y z itakuwa parabola. Uso unakaa juu ya ndege ya x y.$

Wakati sketching nyuso, tumeona kwamba ni muhimu kwa mchoro makutano ya uso na ndege sambamba na moja ya ndege kuratibu. Curves hizi huitwa athari. Tunaweza kuwaona katika njama ya silinda katika Kielelezo$\PageIndex{6}$.

Ufafanuzi: athari

Mwelekeo wa uso ni sehemu za msalaba zilizoundwa wakati uso unapounganisha ndege sambamba na moja ya ndege za kuratibu.

Mwelekeo ni muhimu katika nyuso za cylindrical sketching. Kwa silinda katika vipimo vitatu, ingawa, seti moja tu ya athari ni muhimu. Angalia, katika Kielelezo$\PageIndex{6}$, kwamba maelezo ya grafu ya$ z=\sin x$ xz -ndege ni muhimu katika kujenga grafu. Mtazamo katika ndege ya xy, ingawa, ni mfululizo wa mistari sambamba, na maelezo katika yz -plane ni mstari mmoja tu.

Takwimu hii ina picha mbili. Picha ya kwanza ni uso. sehemu ya msalaba wa uso sambamba na x z ndege itakuwa sine Curve. Picha ya pili ni safu ya sine katika ndege ya x y. — Kielelezo$\PageIndex{6}$: (a) Hii ni mtazamo mmoja wa grafu ya equation$ z=\sin x$. (b) Ili kupata maelezo ya grafu katika$xz$ -ndege, weka$ y=0$. Mtazamo ni wimbi la sine mbili tu.

Nyuso za cylindrical zinaundwa na seti ya mistari sambamba. Sio nyuso zote katika vipimo vitatu zimejengwa kwa urahisi, hata hivyo. Sasa tunachunguza nyuso ngumu zaidi, na athari ni chombo muhimu katika uchunguzi huu.

Quadric nyuso

Tumejifunza kuhusu nyuso katika vipimo vitatu vilivyoelezwa na equations ya kwanza; hizi ni ndege. Aina nyingine za kawaida za nyuso zinaweza kuelezewa na equations ya pili. Tunaweza kuona nyuso hizi kama upanuzi tatu-dimensional ya sehemu conic sisi kujadiliwa mapema: duaradufu, parabola, na hyperbola. Tunaita nyuso hizi za quadric grafu

Ufafanuzi: nyuso za Quadric na sehemu za conic

Nyuso za Quadric ni grafu ya equations ambayo inaweza kuelezwa kwa fomu

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Wakati uso wa quadric unapounganisha ndege ya kuratibu, maelezo ni sehemu ya conic.

ellipsoid ni uso ilivyoelezwa na equation ya fomu$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1.$$ x=0$ Kuweka kuona maelezo ya ellipsoid katika yz -ndege. Kuona athari katika$xy$ - na$xz$ -ndege, kuweka$ z=0$ na$ y=0$, kwa mtiririko huo. Angalia kwamba, ikiwa$ a=b$, maelezo katika$xy$ -ndege ni mduara. Vile vile$ a=c$, ikiwa, maelezo katika$xz$ -ndege ni mduara na, ikiwa$ b=c$, basi ufuatiliaji katika$yz$ -ndege ni mduara. Aina, basi, ni ellipsoid na$ a=b=c.$

Mfano$ \PageIndex{2}$: Sketching an Ellipsoid

Mchoro ellipsoid

\[ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1. \nonumber \]

Suluhisho

Anza kwa sketching athari. Ili kupata maelezo katika xy -plane, weka$ z=0: \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}=1$ (Kielelezo$\PageIndex{7}$). Ili kupata athari nyingine, kuweka kwanza$ y=0$ na kisha kuweka$ x=0.$

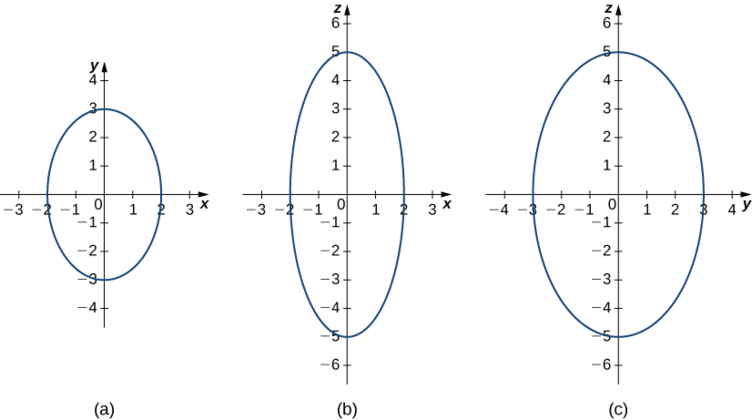
Takwimu hii ina picha tatu. Picha ya kwanza ni mviringo unaozingatia asili ya mfumo wa kuratibu mstatili. Inaingiliana na mhimili x saa -2 na 2. Inaingiliana na mhimili wa y saa -3 na 3. Picha ya pili ni mviringo unaozingatia asili ya mfumo wa kuratibu mstatili. Inaingiliana na mhimili wa x saa -2 na 2 na y-axis saa -5 na 5. Picha ya tatu ni mviringo unaozingatia asili ya mfumo wa kuratibu mstatili. Inaingiliana na x-axis saa -3 na 3 na y-axis saa -5 na 5. — Kielelezo$\PageIndex{7}$: (a) Grafu hii inawakilisha maelezo ya equation$ \dfrac{x^2}{2^2}+\dfrac{y^2}{3^2}+\dfrac{z^2}{5^2}=1$ katika$xy$ -ndege, wakati sisi kuweka$ z=0$. (b) Tunapoweka$ y=0$, tunapata maelezo ya ellipsoid katika$xz$ -plane, ambayo ni ellipse. (c) Tunapoweka$ x=0$, tunapata maelezo ya ellipsoid katika$yz$ -plane, ambayo pia ni ellipse.

Sasa kwa kuwa tunajua nini athari za kuangalia hii imara, tunaweza kuchora uso katika vipimo vitatu (Kielelezo$\PageIndex{8}$).

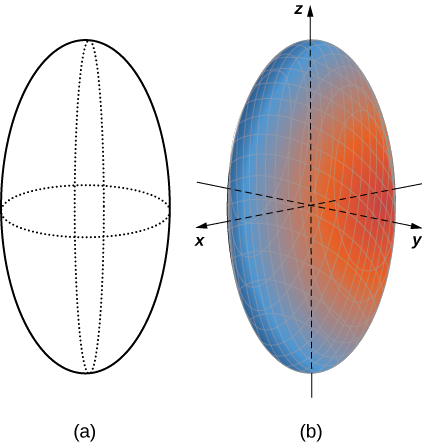
Takwimu hii ina picha mbili. Picha ya kwanza ni ellipse ya wima. Kuna curves mbili inayotolewa na mistari iliyopigwa karibu na kituo cha usawa na kwa wima ili kutoa picha ya sura ya 3-dimensional. Picha ya pili ni sura imara ya elliptical na katikati ya asili ya mfumo wa kuratibu 3-dimensional. — Kielelezo$\PageIndex{8}$: (a) Athari hutoa mfumo wa uso. (b) Katikati ya ellipsoid hii ni asili.

Mtazamo wa ellipsoid ni ellipse katika kila ndege za kuratibu. Hata hivyo, hii haipaswi kuwa kesi kwa nyuso zote za quadric. Nyuso nyingi za quadric zina athari ambazo ni aina tofauti za sehemu za conic, na hii huonyeshwa kwa jina la uso. Kwa mfano, kama uso unaweza kuelezewa na equation ya fomu

\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=\dfrac{z}{c} \nonumber \]

basi sisi wito kwamba uso paraboloid elliptic. Mtazamo katika ndege ya xy ni duaradufu, lakini athari katika xz- ndege na yz -ndege ni parabolas (Kielelezo$\PageIndex{9}$). Paraboloids nyingine ya elliptic inaweza kuwa na mwelekeo mwingine tu kwa kubadilishana vigezo kutupa variable tofauti katika muda linear ya equation$ \dfrac{x^2}{a^2}+\dfrac{z^2}{c^2}=\dfrac{y}{b}$ au$ \dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=\dfrac{x}{a}$.

Takwimu hii ni picha ya uso. Ni katika mfumo wa kuratibu 3-dimensional juu ya asili. Sehemu ya msalaba wa uso huu sambamba na ndege ya x y itakuwa duaradufu. — Kielelezo$\PageIndex{9}$: Sehemu hii ya quadric inaitwa paraboloid elliptic.

Mfano$ \PageIndex{3}$: Identifying Traces of Quadric Surfaces

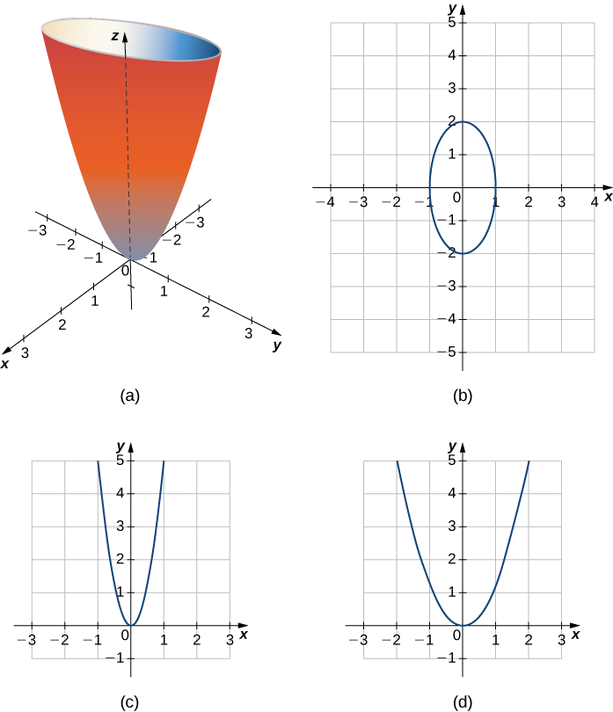
Eleza athari za paraboloid ya elliptic$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$.

Suluhisho

Ili kupata maelezo katika$xy$ -ndege, weka$ z=0: x^2+\dfrac{y^2}{2^2}=0.$ Mtazamo katika ndege$ z=0$ ni hatua moja tu, asili. Kwa kuwa hatua moja haituambii sura ni nini, tunaweza kuhamisha$z$ -axis kwa ndege ya kiholela ili kupata sura ya athari nyingine za takwimu.

Mtazamo katika ndege$ z=5$ ni grafu ya equation$ x^2+\dfrac{y^2}{2^2}=1$, ambayo ni ellipse. Katika$xz$ -ndege, equation inakuwa$ z=5x^2$. Mtazamo ni parabola katika ndege hii na katika ndege yoyote yenye equation$ y=b$.

Katika ndege sambamba na$yz$ -ndege, athari pia ni parabolas, kama tunaweza kuona katika Kielelezo$\PageIndex{10}$.

Takwimu hii ina picha nne. Picha ya kwanza ni picha ya uso. Ni katika mfumo wa kuratibu 3-dimensional juu ya asili. Sehemu ya msalaba wa uso huu sambamba na ndege ya x y itakuwa duaradufu. Sehemu ya msalaba sambamba na ndege ya x z itakuwa parabola. Sehemu ya msalaba ya uso sambamba na ndege y z itakuwa parabola. Picha ya pili ni sehemu ya msalaba inayofanana na ndege ya x y na ni duaradufu. Picha ya tatu ni sehemu ya msalaba inayofanana na ndege ya x z na ni parabola. Picha ya nne ni sehemu ya msalaba inayofanana na ndege ya y z na ni parabola. — Kielelezo$\PageIndex{10}$: (a) Paraboloid$ x^2+\dfrac{y^2}{2^2}=\dfrac{z}{5}$. (b) kufuatilia katika ndege$ z=5$. (c) kuwaeleza katika$xz$ -ndege. (d) kuwaeleza katika$yz$ -ndege.

Zoezi$ \PageIndex{2}$:

Hyperboloid ya karatasi moja ni uso wowote ambao unaweza kuelezewa kwa usawa wa fomu$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1$. Eleza athari za hyperboloid ya karatasi moja iliyotolewa na equation$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1.$

Kidokezo

Ili kupata athari katika ndege za kuratibu, weka kila kutofautiana kwa sifuri moja kwa moja.

Jibu

Athari sambamba na$xy$ -ndege ni ellipses na athari sambamba na$xz$ - na$yz$ -ndege ni hyperbolas. Hasa, maelezo katika$xy$ -plane ni duaradufu$ \dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1,$ kufuatilia katika$xz$ -plane ni hyperbola$ \dfrac{x^2}{3^2}−\dfrac{z^2}{5^2}=1,$ na kufuatilia katika$yz$ -plane ni hyperbola$ \dfrac{y^2}{2^2}−\dfrac{z^2}{5^2}=1$ (angalia takwimu zifuatazo).

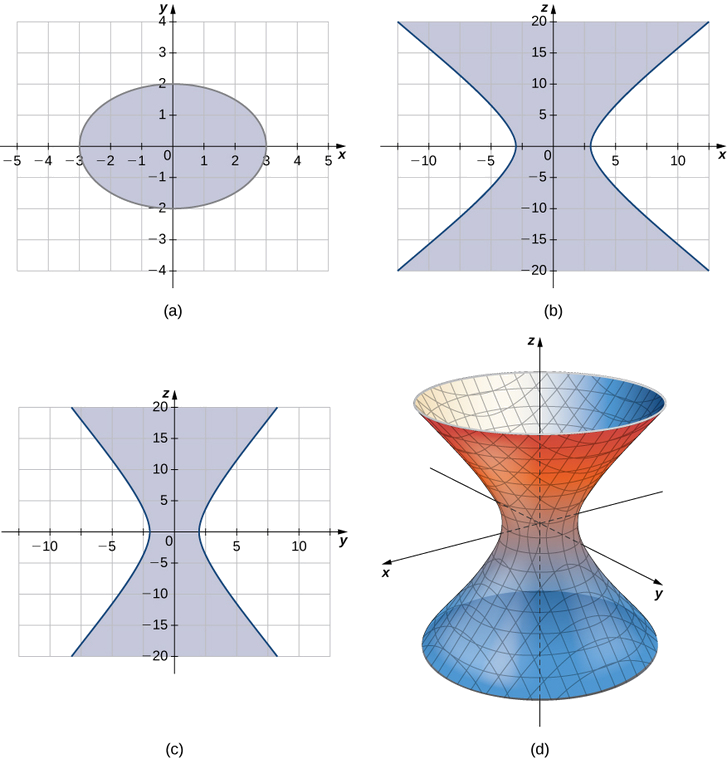
$Takwimu hii ina picha nne. Picha ya kwanza ni ellipse iliyozingatia asili ya mfumo wa kuratibu mstatili. Inaingiliana na mhimili x saa -3 na 3. Inaingiliana na mhimili y saa -2 na 2. Picha ya pili ni grafu ya hyperbola. Ni curves mbili kufungua moja katika mwelekeo hasi x na moja linganifu katika chanya x mwelekeo. Picha ya tatu ni grafu ya hyperbola katika ndege ya y z. Inafungua katika mwelekeo mbaya y na ufunguzi wa safu ya ulinganifu katika mwelekeo y chanya. Picha ya nne ni uso wa 3-dimensional. Ni sehemu ya juu na chini ya msalaba itakuwa mviringo. Makutano ya wima itakuwa hyperbola.$

Hyperboloids ya karatasi moja ina mali ya kuvutia. Kwa mfano, wanaweza kujengwa kwa kutumia mistari ya moja kwa moja, kama vile katika uchongaji katika Kielelezo$\PageIndex{11a}$. Kwa kweli, minara ya baridi ya mimea ya nyuklia mara nyingi hujengwa kwa sura ya hyperboloid. Wajenzi wanaweza kutumia mihimili ya chuma moja kwa moja katika ujenzi, ambayo inafanya minara imara sana wakati wa kutumia nyenzo kidogo (Kielelezo$\PageIndex{11b}$).

Takwimu hii ina picha mbili. Picha ya kwanza ni uchongaji uliofanywa kwa vijiti vinavyolingana, vilivyounganishwa pamoja katika mduara na sehemu ya msalaba wa hyperbolic. Picha ya pili ni mmea wa nguvu za nyuklia. Minara ni umbo la hyperbolic. — Kielelezo$\PageIndex{11}$: (a) Uchongaji katika sura ya hyperboloid unaweza kujengwa kwa mistari ya moja kwa moja. (b) Minara ya baridi kwa mimea ya nyuklia mara nyingi hujengwa kwa sura ya hyperboloid.

Mfano$ \PageIndex{4}$: Chapter Opener: Finding the Focus of a Parabolic Reflector

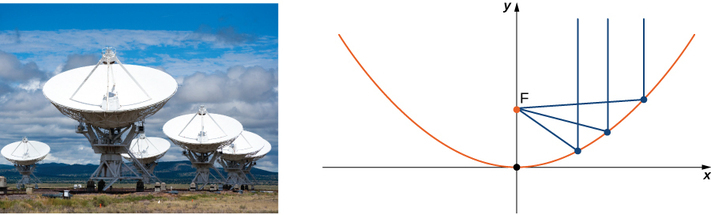
Nishati kupiga uso wa kutafakari parabolic ni kujilimbikizia katika hatua kuu ya kutafakari (Kielelezo$\PageIndex{12}$). Kama uso wa reflector parabolic ni ilivyoelezwa na equation$ \dfrac{x^2}{100}+\dfrac{y^2}{100}=\dfrac{z}{4},$ ambapo ni hatua ya msingi ya reflector?

Takwimu hii ina picha mbili. Picha ya kwanza ni picha ya sahani za satelaiti na watafakari wa parabolic. Picha ya pili ni safu ya parabolic kwenye sehemu ya mstari. Kuna sehemu ya mstari perpendicular sehemu nyingine line kupitia V. kuna uhakika juu ya sehemu hii line kinachoitwa F. kuna 3 mistari kutoka F kwa parabola, intersecting katika P ndogo 1, P ndogo 2, na P ndogo 3. Pia kuna mistari mitatu ya wima kutoka P ndogo 1 hadi Q ndogo 1, kutoka P ndogo 2 hadi Q ndogo 2, na kutoka P ndogo 3 hadi Q ndogo 3. — Kielelezo$\PageIndex{12}$: Nishati inaonyesha mbali ya reflector parabolic na hukusanywa katika hatua ya msingi. (mikopo: muundo wa CGP Grey, Wikimedia Commons)

Suluhisho

Kwa kuwa z ni variable ya kwanza ya nguvu, mhimili wa kutafakari unafanana na$z$ -axis. Coefficients ya$ x^2$ and $ y^2$ are equal, so the cross-section of the paraboloid perpendicular to the $z$ -axis ni mduara. Tunaweza kufikiria maelezo katika xz -ndege au yz -ndege; matokeo yake ni sawa. Kuweka$ y=0$, the trace is a parabola opening up along the $z$ -axis, na usawa wa kawaida$ x^2=4pz$, where $ p$ is the focal length of the parabola. In this case, this equation becomes $ x^2=100⋅\dfrac{z}{4}=4pz$ or $ 25=4p$. So p is $ 6.25$ m, which tells us that the focus of the paraboloid is $ 6.25$ m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is $ (0,0,6.25).$

Kumi na saba kiwango quadric nyuso inaweza kuwa inayotokana na equation jumla

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Takwimu zifuatazo zinafupisha muhtasari muhimu zaidi.

Takwimu hii ni ya meza yenye nguzo mbili na safu tatu. Safu tatu zinawakilisha nyuso za kwanza za quadric: ellipsoid, hyperboloid ya karatasi moja, na hyperboloid ya karatasi mbili. Ulinganisho na athari ziko kwenye safu ya kwanza. Safu ya pili ina grafu ya nyuso. Grafu ya ellipsoid ni sura ya mviringo mviringo. Hyperboloid ya karatasi moja ni mviringo juu na chini na nyembamba katikati. Hyperboloid katika karatasi mbili ina domes mbili za parabolic kinyume cha kila mmoja. — Kielelezo$\PageIndex{13}$: Tabia za Nyuso za kawaida za Quadric: Ellipsoid, Hyperboloid ya Karatasi moja, Hyperboloid ya Karatasi mbili.

Takwimu hii ni ya meza yenye nguzo mbili na safu tatu. Safu tatu zinawakilisha nyuso za pili za quadric 6: koni ya elliptic, paraboloid elliptic, na paraboloid ya hyperbolic. Ulinganisho na athari ziko kwenye safu ya kwanza. Safu ya pili ina grafu ya nyuso. Koni ya elliptic ina mbegu mbili zinazogusa pointi. Paraboloidi ya elliptiki inafanana na koni lakini mviringo. Paraboloid ya hyperbolic ina bend katikati sawa na kitanda. — Kielelezo$\PageIndex{14}$: Tabia za Nyuso za kawaida za Quadric: Cone ya elliptic, elliptic Paraboloid, Hyperbolic Paraboloid.

Mfano$ \PageIndex{5}$: Identifying Equations of Quadric Surfaces

Tambua nyuso zinazowakilishwa na equations iliyotolewa.

$ 16x^2+9y^2+16z^2=144$
$ 9x^2−18x+4y^2+16y−36z+25=0$

Suluhisho

a.$ x,y,$ na$ z$ maneno yote ni mraba, na wote ni chanya, hivyo hii pengine ellipsoid. Hata hivyo, hebu kuweka equation katika fomu ya kiwango kwa ellipsoid tu kuwa na uhakika. Tuna

\[ 16x^2+9y^2+16z^2=144. \nonumber \]

Kugawanyika kwa njia ya 144 anatoa

\[ \dfrac{x^2}{9}+\dfrac{y^2}{16}+\dfrac{z^2}{9}=1. \nonumber \]

Kwa hiyo, hii ni, kwa kweli, ellipsoid, iliyozingatia asili.

b Tunaona kwanza kwamba$ z$ neno hilo linafufuliwa tu kwa nguvu ya kwanza, kwa hiyo hii ni paraboloid ya elliptic au paraboloid ya hyperbolic. Pia tunaona kuna$ x$ maneno na$ y$ masharti ambayo si mraba, hivyo uso huu wa quadric haujazingatia asili. Tunahitaji kukamilisha mraba ili kuweka equation hii katika moja ya fomu za kawaida. Tuna

\[ \begin{align*} 9x^2−18x+4y^2+16y−36z+25 =0 \\[4pt] 9x^2−18x+4y^2+16y+25 =36z \\[4pt] 9(x^2−2x)+4(y^2+4y)+25 =36z \\[4pt] 9(x^2−2x+1−1)+4(y^2+4y+4−4)+25 =36z \\[4pt] 9(x−1)^2−9+4(y+2)^2−16+25 =36z \\[4pt] 9(x−1)^2+4(y+2)^2 =36z \\[4pt] \dfrac{(x−1)^2}{4}+\dfrac{(y−2)^2}{9} =z. \end{align*}\]

Hii ni paraboloid elliptic unaozingatia$ (1,2,0).$

Zoezi$ \PageIndex{3}$

Tambua uso unaowakilishwa na equation$ 9x^2+y^2−z^2+2z−10=0.$

Kidokezo: Angalia ishara na nguvu za$ x,y$, na$ z$ masharti
Jibu: Hyperboloid ya karatasi moja, iliyozingatia$ (0,0,1)$.

Dhana muhimu

Seti ya mistari inayofanana na mstari uliotolewa unaopita kupitia pembe iliyotolewa inaitwa silinda, au uso wa cylindrical. Mstari sambamba huitwa maamuzi.
Mfululizo wa uso wa tatu-dimensional na ndege inaitwa kufuatilia. Ili kupata maelezo katika $xy$-, -, au$yz$ $xz$- ndege, kuweka$ z=0,x=0,$ au$ y=0,$ kwa mtiririko huo.
Nyuso za Quadric ni nyuso tatu na mwelekeo unaojumuisha sehemu za conic. Kila uso wa quadric unaweza kuelezwa kwa usawa wa fomu

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0. \nonumber \]

Ili kuchora grafu ya uso wa quadric, kuanza kwa sketching athari kuelewa mfumo wa uso.
Nyuso muhimu za quadric zimefupishwa katika Takwimu$\PageIndex{13}$ na$\PageIndex{14}$.

faharasa

silinda: seti ya mistari sambamba na mstari uliotolewa unaopita kupitia safu iliyotolewa

ellipsoid: uso wa tatu-dimensional ulioelezwa na equation ya fomu$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$; athari zote za uso huu ni ellipses

koni ya elliptic: uso wa tatu-dimensional ulioelezwa na equation ya fomu$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=0$; athari za uso huu ni pamoja na ellipses na mistari intersecting

elliptic paraboloid: uso wa tatu-dimensional ulioelezwa na equation ya fomu$ z=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}$; athari za uso huu ni pamoja na ellipses na parabolas

hyperboloid ya karatasi moja: uso wa tatu-dimensional ulioelezwa na equation ya fomu,$ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1;$ athari za uso huu ni pamoja na ellipses na hyperbolas.

hyperboloid ya karatasi mbili: uso wa tatu-dimensional ulioelezwa na equation ya fomu$ \dfrac{z^2}{c^2}−\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1$; athari za uso huu ni pamoja na ellipses na hyperbolas

nyuso quadric: nyuso katika vipimo vitatu vina mali ambayo athari za uso ni sehemu za conic (ellipses, hyperbolas, na parabolas)

hukumu: mistari sambamba ambayo hufanya uso wa cylindrical

fuatilia: makutano ya uso tatu-dimensional na ndege kuratibu

Ufafanuzi: mitungi na maamuzi

Mfano\( \PageIndex{1}\): Graphing Cylindrical Surfaces

Zoezi\( \PageIndex{1}\):

Ufafanuzi: athari

Ufafanuzi: nyuso za Quadric na sehemu za conic

Mfano\( \PageIndex{2}\): Sketching an Ellipsoid

Mfano\( \PageIndex{3}\): Identifying Traces of Quadric Surfaces

Zoezi\( \PageIndex{2}\):

Mfano\( \PageIndex{4}\): Chapter Opener: Finding the Focus of a Parabolic Reflector

Mfano\( \PageIndex{5}\): Identifying Equations of Quadric Surfaces

Zoezi\( \PageIndex{3}\)