12.5: Ulinganisho wa Mistari na Ndege katika Nafasi
- Page ID
- 178160
- Andika vector, parametric, na equations symmetric ya mstari kupitia hatua fulani katika mwelekeo fulani, na mstari kupitia pointi mbili zilizopewa.
- Pata umbali kutoka kwenye hatua hadi kwenye mstari uliotolewa.
- Andika usawa wa vector na scalar wa ndege kupitia hatua iliyotolewa na kawaida iliyotolewa.
- Pata umbali kutoka kwenye hatua hadi ndege iliyotolewa.
- Pata angle kati ya ndege mbili.
Kwa sasa, tunajua na equations ya kuandika inayoelezea mstari katika vipimo viwili. Kuandika equation kwa mstari, ni lazima kujua pointi mbili kwenye mstari, au ni lazima kujua mwelekeo wa mstari na angalau hatua moja kwa njia ambayo mstari hupita. Katika vipimo viwili, tunatumia dhana ya mteremko kuelezea mwelekeo, au mwelekeo, wa mstari. Katika vipimo vitatu, tunaelezea mwelekeo wa mstari kwa kutumia vector sambamba na mstari. Katika sehemu hii, tunachunguza jinsi ya kutumia equations kuelezea mistari na ndege katika nafasi.
Ulinganisho wa Mstari katika Nafasi
Hebu kwanza tuchunguze nini maana ya vectors mbili kuwa sambamba. Kumbuka kwamba vectors sambamba lazima iwe na maelekezo sawa au kinyume. Kama mbili nonzero wadudu,\( \vecs{u}\) na\( \vecs{v}\), ni sambamba, sisi kudai lazima kuna scalar\( k\), kama kwamba\( \vecs{u}=k\vecs{v}\). Ikiwa\( \vecs{u}\) na\( \vecs{v}\) uwe na mwelekeo huo, chagua tu
\[ k=\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]
Ikiwa\( \vecs{u}\) na\( \vecs{v}\) uwe na maelekezo tofauti, chagua
\[ k=−\dfrac{‖\vecs{u}‖}{‖\vecs{v}‖}. \nonumber \]
Kumbuka kuwa mazungumzo anashikilia pia. Ikiwa\( \vecs{u}=k \vecs{v}\) kwa scalar fulani\( k\), basi ama\( \vecs{u}\) na\(\vecs{ v}\) uwe na mwelekeo sawa\( (k>0)\) au maelekezo kinyume\( (k<0)\), hivyo\( \vecs{u}\) na\( \vecs{v}\) ni sawa. Kwa hiyo, vectors mbili nonzero\( \vecs{u}\) na\(\vecs{ v}\) ni sambamba kama na tu kama\( \vecs{u}=k\vecs{v}\) kwa baadhi scalar\( k\). Kwa mkataba, vector sifuri\( \vecs{0}\) inachukuliwa kuwa sawa na wadudu wote.
Kielelezo\(\PageIndex{1}\): Vector\(\vecs{v}\) ni mwelekeo vector kwa\( \vecd{PQ}\).
Kama ilivyo katika vipimo viwili, tunaweza kuelezea mstari katika nafasi kwa kutumia hatua kwenye mstari na mwelekeo wa mstari, au vector sambamba, ambayo tunaita vector mwelekeo (Kielelezo\(\PageIndex{1}\)). Hebu\( L\) kuwa mstari katika nafasi inayopitia hatua\( P(x_0,y_0,z_0)\). Hebu\( \vecs{v}=⟨a,b,c⟩\) kuwa vector sambamba na\( L\). Kisha, kwa hatua yoyote juu ya mstari\( Q(x,y,z)\), tunajua kwamba\( \vecd{PQ}\) ni sambamba na\( \vecs{v}\). Hivyo, kama sisi tu kujadiliwa, kuna scalar\( t\), kama kwamba\( \vecd{PQ}=t\vecs{v}\), ambayo inatoa
\ [kuanza {align}\ vecd {PQ} &=t\ vecs {v}\ hakuna nambari\\ [4pt]
|x-x_0, y-y_0, z-z_0th & =ta, b,\ nonumber\\ [4pt]
|x-x_0, y-y_0, z-z_0& =ta, tab, tectra. \ studio {eq1}\ mwisho {align}\]
Kutumia shughuli za vector, tunaweza kuandika upya Equation\ ref {eq1}
\ [kuanza {align*} x-x_0, y-y_0, z-z_0asis &=ta, tb, tculf\\ [4pt]
, y, zππx_0, y_0, z_0cus & =tve/a, b, chumen\\ [4pt]
\ underbrace {acute, y, y,} _ {vecs {r}} &=\ underbrace {x_0, y_0, z_0} _ {\ vecs {r} _o} +t\ underbrace {a, b, ccass} _ {\ vecs {v}}}. \ mwisho {align*}\]
Kuweka\( \vecs{r}=⟨x,y,z⟩\) na\( \vecs{r}_0=⟨x_0,y_0,z_0⟩\), sasa tuna equation vector ya mstari:
\[ \vecs{r}=\vecs{r}_0+t\vecs{v}. \label{vector} \]
Kulinganisha vipengele, Equation\ ref {vector} inaonyesha kwamba equations zifuatazo ni wakati huo huo kweli:\( x−x_0=ta, y−y_0=tb,\) na\( z−z_0=tc.\) Kama sisi kutatua kila moja ya milinganyo haya kwa vigezo sehemu\( x,y,\) na\( z\), sisi kupata seti ya milinganyo ambayo kila variable hufafanuliwa katika suala la parameter \(t\)na kwamba, pamoja, kuelezea mstari. Seti hii ya milinganyo mitatu inaunda seti ya milinganyo ya parametric ya mstari:
\[ x=x_0+ta \nonumber \]
\[ y=y_0+tb \nonumber \]
\[ z=z_0+tc.\nonumber \]
Kama sisi kutatua kila moja ya equations kwa\( t\) kuchukua\( a,b\), na\( c\) ni nonzero, sisi kupata maelezo tofauti ya mstari huo:
\[ \begin{align*} \dfrac{x−x_0}{a} =t \\[4pt] \dfrac{y−y_0}{b} =t \\[4pt] \dfrac{z−z_0}{c} =t.\end{align*}\]
Kwa sababu kila kujieleza sawa\(t\), wote wana thamani sawa. Tunaweza kuwaweka sawa kwa kila mmoja ili kuunda equations symmetric ya mstari:
\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]
Sisi muhtasari matokeo katika theorem ifuatayo.
Mstari\( L\) unaofanana\( \vecs{v}=⟨a,b,c⟩\) na vector na kupitia hatua\( P(x_0,y_0,z_0)\) unaweza kuelezewa na equations zifuatazo za parametric:
\[ x=x_0+ta, y=y_0+tb, \nonumber \]
na
\[ z=z_0+tc. \nonumber \]
Ikiwa mara kwa mara\( a,b,\) na\( c\) sio zero, basi\( L\) inaweza kuelezewa na usawa wa mstari wa mstari:
\[\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}. \nonumber \]
Ulinganisho wa parametric wa mstari sio wa kipekee. Kutumia vector tofauti sambamba au hatua tofauti kwenye mstari inaongoza kwa uwakilishi tofauti, sawa. Kila seti ya milinganyo ya parametric inaongoza kwa seti inayohusiana ya equations symmetric, hivyo inafuata kwamba equation ya mstari wa mstari sio ya kipekee ama.
Pata usawa wa parametric na ulinganifu wa mstari unaopita kupitia pointi\( (1,4,−2)\) na\( (−3,5,0).\)
Suluhisho
Kwanza, tambua vector sambamba na mstari:
\[ \vecs v=⟨−3−1,5−4,0−(−2)⟩=⟨−4,1,2⟩. \nonumber \]
Tumia mojawapo ya pointi zilizotolewa kwenye mstari ili kukamilisha usawa wa parametric:
\[\begin{align*} x =1−4t \\[4pt] y =4+t, \end{align*}\]
na
\[ z=−2+2t. \nonumber \]
Kutatua kila equation\( t\) kwa kujenga equation symmetric ya mstari:
\[ \dfrac{x−1}{−4}=y−4=\dfrac{z+2}{2}. \nonumber \]
Pata usawa wa parametric na ulinganifu wa mstari unaopita kupitia pointi\( (1,−3,2)\) na\( (5,−2,8).\)
- Kidokezo:
-
Anza kwa kutafuta vector sambamba na mstari.
- Jibu
-
Seti inayowezekana ya equations parametric: seti\( x=1+4t,\; y=−3+t,\; z=2+6t;\) inayohusiana ya equations symmetric:\[ \dfrac{x−1}{4}=y+3=\dfrac{z−2}{6} \nonumber \]
Wakati mwingine hatutaki equation ya mstari mzima, tu sehemu line. Katika kesi hii, tunapunguza maadili ya parameter yetu\( t\). Kwa mfano, basi\( P(x_0,y_0,z_0)\) na\( Q(x_1,y_1,z_1)\) kuwa pointi kwenye mstari, na basi\( \vecs p=⟨x_0,y_0,z_0⟩\) na\( \vecs q=⟨x_1,y_1,z_1⟩\) kuwa kuhusishwa nafasi wadudu. Kwa kuongeza, basi\(\vecs r=⟨x,y,z⟩\). Tunataka kupata vector equation kwa sehemu line kati\( P\) na\( Q\). Kutumia\( P\) kama hatua yetu inayojulikana kwenye mstari, na\( \vecd{PQ}=⟨x_1−x_0,y_1−y_0,z_1−z_0⟩\) kama mwelekeo wa vector equation, Equation\ ref {vector} inatoa
\[\vecs{r}=\vecs{p}+t(\vecd{PQ}). \label{eq10} \]
Equation\ ref {eq10} inaweza kupanuliwa kwa kutumia mali ya wadudu:
\ [kuanza {align*}\ vecs {r} &=\ vecs {p} +t (\ vecd {PQ})\\ [4pt]
&=x_0, y_0, z_0+tf/x_1,1-x_0, y_1,1-y_0,
z_1,1-z_0cents\\ [4pt] &=12x_0, y_0, z_0+t (x_1, y_1, z_1πx_0, y_0, z_0)\\ [4pt]
&=x_0, y_0, z_0+tconfex_1, y_1, z_1-t_x_0, y_0, z_0\\ pt]
& =( 1,1t) x_0, y_0 , z_0+tf/x_1, y_1, z_1\ [4pt]
& =( 1-t)\ vecs {p} +t\ vecs {q}. \ mwisho {align*}\]
Hivyo, equation vector ya mstari kupita kupitia\( P\) na\( Q\) ni
\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q}. \nonumber \]
Kumbuka kwamba hatukutaka equation ya mstari mzima, tu sehemu line kati\( P\) na\( Q\). Kumbuka kwamba wakati\( t=0\), tuna\(\vecs{r}=\vecs{p}\), na wakati\( t=1\), tuna\( \vecs r=\vecs q\). Kwa hiyo, equation vector ya sehemu line kati\( P\) na\( Q\) ni
\[\vecs{r}=(1−t)\vecs{p}+t\vecs{q},0≤t≤1. \nonumber \]
Kurudi kwenye Equation\ ref {vector}, tunaweza pia kupata equations parametric kwa sehemu hii ya mstari. Tuna
\ [kuanza {align*}\ vecs {r} &=\ vecs {p} +t (\ vecd {PQ})\\ [4pt]
+x, y, &=x_0, y_0, z_0+tconfex_1,1-x_0, y_1,1-z_0\ [4pt]
&=x_0+t (x_1,1-x_0), y_0+t (y_1,1-y_0), z_0+t (z_1—z_0). \ mwisho {align*}\]
Kisha, equations parametric ni
\[ \begin{align*} x &=x_0+t(x_1−x_0) \\[4pt] y &=y_0+t(y_1−y_0) \\[4pt] z &=z_0+t(z_1−z_0), \quad 0≤t≤1. \end{align*} \label{para} \]
Pata usawa wa parametric wa sehemu ya mstari kati ya pointi\( P(2,1,4)\) na\( Q(3,−1,3).\)
Suluhisho
Anza na equations parametric kwa mstari (Equations\ ref {para}) na kazi na kila sehemu tofauti:
\[ \begin{align*} x &=x_0+t(x_1−x_0)\\[4pt] &=2+t(3−2)\\[4pt] &=2+t, \end{align*}\]
\[ \begin{align*} y &=y_0+t(y_1−y_0)\\[4pt] &=1+t(−1−1)\\[4pt] &=1−2t, \end{align*}\]
na
\[ \begin{align*} z &=z_0+t(z_1−z_0)\\[4pt] &=4+t(3−4)\\[4pt] &=4−t. \end{align*}\]
Kwa hiyo, equations parametric kwa sehemu ya mstari ni
\[ \begin{align*} x &=2+t\\[4pt] y &=1−2t\\[4pt] z &=4−t,\quad 0≤t≤1.\end{align*}\]
Pata usawa wa parametric wa sehemu ya mstari kati ya pointi\( P(−1,3,6)\) na\( Q(−8,2,4)\).
- Jibu
-
\( x=−1−7t,\; y=3−t,\; z=6−2t, \quad 0≤t≤1 \)
Umbali kati ya Point na Line
Tayari tunajua jinsi ya kuhesabu umbali kati ya pointi mbili katika nafasi. Sasa tunapanua ufafanuzi huu kuelezea umbali kati ya uhakika na mstari katika nafasi. Kadha kadhaa za ulimwengu halisi zipo wakati ni muhimu kuwa na uwezo wa kuhesabu umbali huu. Wakati wa kujenga nyumba, kwa mfano, wajenzi wanapaswa kuzingatia mahitaji ya “kurudi”, wakati miundo au rasilimali zinapaswa kuwa umbali fulani kutoka kwenye mstari wa mali. Usafiri wa hewa hutoa mfano mwingine. Ndege za ndege zina wasiwasi kuhusu umbali kati ya maeneo ya wakazi na njia zilizopendekezwa za ndege.
Hebu\( L\) kuwa mstari katika ndege na basi\( M\) kuwa na uhakika wowote si kwenye mstari. Kisha, tunafafanua umbali\( d\) kutoka\( M\) kwa\( L\) kama urefu wa sehemu ya mstari\( \overline{MP}\), ambapo\( P\) ni uhakika juu ya\( L\) vile kwamba\( \overline{MP}\) ni perpendicular kwa\( L\) (Kielelezo\(\PageIndex{2}\)).
Wakati sisi ni kuangalia kwa umbali kati ya mstari na uhakika katika nafasi, Kielelezo\(\PageIndex{2}\) bado inatumika. Bado tunafafanua umbali kama urefu wa sehemu ya mstari wa perpendicular kuunganisha uhakika kwa mstari. Katika nafasi, hata hivyo, hakuna njia ya wazi ya kujua ni hatua gani kwenye mstari hujenga sehemu ya mstari wa perpendicular, kwa hiyo tunachagua hatua ya kiholela kwenye mstari na kutumia mali ya vectors kuhesabu umbali. Kwa hiyo, hebu\( P\) kuwa hatua ya kiholela kwenye mstari\( L\) na uache\(\vecs{v}\) kuwa vector mwelekeo kwa\( L\) (Kielelezo\(\PageIndex{3}\)).
Vectors\( \vecd{PM}\) na\(\vecs{v}\) kuunda pande mbili za parallelogram na eneo\( ‖\vecd{PM}×\vecs{v}‖\). Kutumia formula kutoka jiometri, eneo la parallelogram hii pia linaweza kuhesabiwa kama bidhaa ya msingi na urefu wake:
\[‖\vecd{PM}×\vecs{v}‖=‖\vecs v‖d. \nonumber \]
Tunaweza kutumia formula hii ili kupata formula ya jumla kwa umbali kati ya mstari katika nafasi na hatua yoyote si kwenye mstari.
Hebu\( L\) kuwa mstari katika nafasi inayopitia hatua\( P\) na vector mwelekeo\(\vecs{v}\). Kama\( M\) ni hatua yoyote si juu\( L\), basi umbali kutoka\( M\) kwa\( L\) ni
\[d=\dfrac{‖\vecd{PM}×\vecs{v}‖}{‖\vecs{v}‖}. \nonumber \]
Pata umbali kati ya hatua\( M=(1,1,3)\) na mstari\( \dfrac{x−3}{4}=\dfrac{y+1}{2}=z−3.\)
Suluhisho:
Kutoka kwa usawa wa mstari, tunajua kwamba vector\( \vecs{v}=⟨4,2,1⟩\) ni vector mwelekeo kwa mstari. Kuweka equations symmetric ya mstari sawa na sifuri, tunaona kwamba hatua\( P(3,−1,3)\) iko juu ya mstari. Kisha,
\[\begin{align*} \vecd{PM} =⟨1−3,1−(−1),3−3⟩\\[4pt] =⟨−2,2,0⟩. \end{align*}\]
Ili kuhesabu umbali, tunahitaji kupata\( \vecd{PM}×\vecs v:\)
\ [kuanza {align*}\ vecd {PM} ×\ vecs {v} &=\ kuanza {vmatrix}\ hisabati {\ kofia i} &\ mathbf {\ kofia j} &\ hatbf {\ kofia k}\\ -1 & 2 & 2 & 1\ mwisho {matrix}\\ [4pt] &= (2—0)\ mathbf {\ kofia i} - (-2,10)\ mathbf {\ kofia j} + (-4-4-8)\ mathbf {\ kofia k}\\ [4pt]
&=2\ mathbf {\ kofia i} +2\ mathbf {\ kofia j} -12\ mathbf {\ kofia k}. \ mwisho {align*}\]
Kwa hiyo, umbali kati ya uhakika na mstari ni (Kielelezo\(\PageIndex{4}\))
\ [kuanza {align*} d &=\ dfrac {合\ vecd {PM} ×\ vecs {v}} {v}} {\ vecs {v}}\\ [4pt]
&=\ dfrac {2 ^ 2^2^2^2}} {\ sqrt {4^2+2^2}}\\ [4pt]
&=\ drac {2\ sqrt {38}} {\ sqrt {21}}\\ [4pt]
&=\ drac {2\ sqrt {798}} {21}\,\ maandishi {vitengo}\ mwisho {align*}\]

Pata umbali kati ya uhakika\( (0,3,6)\) na mstari na usawa wa parametric\( x=1−t,\; y=1+2t,\; z=5+3t.\)
- Kidokezo
-
Pata vector na hatua ya awali\( (0,3,6)\) na hatua ya mwisho kwenye mstari, na kisha upate vector ya mwelekeo kwa mstari.
- Jibu
-
\( \sqrt{\dfrac{10}{7}} = \dfrac{\sqrt{70}}{7} \,\text{units} \)
Uhusiano kati ya mistari
Kutokana na mistari miwili katika ndege mbili-dimensional, mistari ni sawa, ni sambamba lakini si sawa, au wao intersect katika hatua moja. Katika vipimo vitatu, kesi ya nne inawezekana. Ikiwa mistari miwili katika nafasi haipatikani, lakini usiingiliane, basi mistari inasemekana kuwa mistari ya skew (Kielelezo\(\PageIndex{5}\)).
Kielelezo\(\PageIndex{5}\): Katika vipimo vitatu, inawezekana kwamba mistari miwili haipatikani, hata wakati wana maelekezo tofauti.
Ili kuainisha mistari kama sambamba lakini si sawa, sawa, intersecting, au skew, tunahitaji kujua mambo mawili: kama vectors mwelekeo ni sambamba na kama mistari kushiriki uhakika (Kielelezo\(\PageIndex{6}\)).
Kwa kila jozi ya mistari, onyesha kama mistari ni sawa, sambamba lakini si sawa, skew, au intersecting.
a.
- \( L_1:\; x=2s−1, \; y=s−1, \; z=s−4\)
- \( L_2: \; x=t−3, \; y=3t+8, \; z=5−2t\)
b.
- \( L_1: \; x=−y=z\)
- \( L_2:\; \dfrac{x−3}{2}=y=z−2\)
c.
- \( L_1:\; x=6s−1,\; y=−2s,\; z=3s+1\)
- \( L_2:\; \dfrac{x−4}{6}=\dfrac{y+3}{−2}=\dfrac{z−1}{3}\)
Suluhisho
a Line\( L_1\) ina mwelekeo vector\( \vecs v_1=⟨2,1,1⟩\); line\( L_2\) ina mwelekeo vector\( \vecs v_2=⟨1,3,−2⟩\). Kwa sababu vectors mwelekeo si vectors sambamba, mistari ni ama intersecting au skew. Kuamua kama mistari intersect, tunaona kama kuna uhakika\( (x,y,z)\), kwamba uongo juu ya mistari yote. Ili kupata hatua hii, tunatumia equations parametric kujenga mfumo wa usawa:
\[ 2s−1=t−3; \nonumber \]
\[ s−1=3t+8; \nonumber \]
\[ s−4=5−2t. \nonumber \]
By equation kwanza,\( t=2s+2.\) Kubadilisha katika mazao ya pili equation
\( s−1=3(2s+2)+8\)
\( s−1=6s+6+8\)
\( 5s=−15\)
\( s=−3.\)
Kubadilishwa katika equation ya tatu, hata hivyo, hutoa utata:
\( s−4=5−2(2s+2)\)
\( s−4=5−4s−4\)
\( 5s=5\)
\( s=1.\)
Hakuna hatua moja ambayo inatimiza usawa wa parametric\( L_1\) na\( L_2\) wakati huo huo. Mstari huu hauingiliani, kwa hiyo ni skew (angalia takwimu zifuatazo).
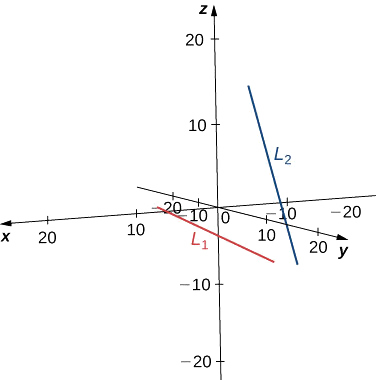
b Line\( L_1\) ina mwelekeo vector\( \vecs v_1=⟨1,−1,1⟩\) na hupita kwa njia ya asili,\( (0,0,0)\). Line\( L_2\) ina tofauti mwelekeo vector\( \vecs v_2=⟨2,1,1⟩\),, hivyo mistari haya si sambamba au sawa. Hebu\( r\) kuwakilisha parameter kwa mstari\( L_1\) na basi\(s\) kuwakilisha parameter kwa\( L_2\):
\[\begin{align*} &\text{Line }L_1: & & \text{Line }L_2:\\[4pt] &x = r & & x = 2s + 3\\[4pt] &y = -r & & y = s \\[4pt] &z = r & & z = s + 2 \end{align*}\]
Tatua mfumo wa equations kupata\( r=1\) na\( s=−1\). Ikiwa tunahitaji kupata hatua ya makutano, tunaweza kubadilisha vigezo hivi katika equations ya awali ili kupata\( (1,−1,1)\) (angalia takwimu zifuatazo).

c. mistari\( L_1\) na\( L_2\) kuwa sawa mwelekeo wadudu:\( \vecs v=⟨6,−2,3⟩.\) Hizi mistari miwili ni sambamba (angalia takwimu zifuatazo).

Eleza uhusiano kati ya mistari na equations zifuatazo za parametric:
\[ x=1−4t, \; y=3+t, \; z=8−6t \nonumber \]
\[x=2+3s,\; y=2s,\; z=−1−3s. \nonumber \]
- Kidokezo
-
Anza kwa kutambua vectors mwelekeo kwa kila mstari. Je, moja ni nyingi ya nyingine?
- Jibu
-
Mstari huu ni skew kwa sababu vectors yao mwelekeo si sambamba na hakuna uhakika\( (x,y,z)\) kwamba liko juu ya mistari yote.
Ulinganifu kwa Ndege
Tunajua kwamba mstari umewekwa na pointi mbili. Kwa maneno mengine, kwa pointi mbili tofauti, kuna mstari mmoja ambao hupita kupitia pointi hizo, iwe katika vipimo viwili au tatu. Vile vile, kutokana na pointi tatu ambazo sio zote ziko kwenye mstari huo, kuna ndege ya pekee inayopita kupitia pointi hizi. Kama vile mstari umewekwa na pointi mbili, ndege imedhamiriwa na tatu.
Hii inaweza kuwa njia rahisi zaidi ya kuashiria ndege, lakini tunaweza kutumia maelezo mengine pia. Kwa mfano, kutokana na mistari miwili tofauti, inayoingiliana, kuna ndege moja iliyo na mistari miwili. Ndege pia imedhamiriwa na mstari na hatua yoyote ambayo haina uongo kwenye mstari. Tabia hizi zinatokea kwa kawaida kutokana na wazo kwamba ndege imedhamiriwa na pointi tatu. Labda tabia ya kushangaza zaidi ya ndege ni kweli muhimu sana.
Fikiria jozi ya vectors orthogonal kwamba kushiriki hatua ya awali. Tazama kunyakua moja ya vectors na kuifuta. Kama twist, vector nyingine huzunguka karibu na sweeps nje ya ndege. Hapa, sisi kuelezea kwamba dhana hesabu. Hebu\(\vecs{n}=⟨a,b,c⟩\) kuwa vector na\(P=(x_0,y_0,z_0)\) uwe na uhakika. Kisha seti ya pointi zote ambazo\(Q=(x,y,z)\)\(\vecd{PQ}\) ni orthogonal\(\vecs{n}\) kuunda ndege (Kielelezo\(\PageIndex{7}\)). Tunasema kwamba\(\vecs{n}\) ni vector ya kawaida, au perpendicular kwa ndege. Kumbuka, bidhaa ya dot ya vectors orthogonal ni sifuri. Ukweli huu huzalisha equation ya vector ya ndege:
\[\vecs{n}⋅\vecd{PQ}=0. \nonumber \]
Kuandika upya equation hii hutoa njia za ziada za kuelezea ndege:
\[ \begin{align*} \vecs{n}⋅\vecd{PQ} &=0 \\[4pt] ⟨a,b,c⟩⋅⟨x−x_0,y−y_0,z−z_0⟩ &=0 \\[4pt] a(x−x_0)+b(y−y_0)+c(z−z_0) &=0. \end{align*}\]
Kutokana na hatua\(P\) na vector\(\vecs n\), seti ya pointi zote\(Q\) zinazolidhisha equation\(\vecs n⋅\vecd{PQ}=0\) huunda ndege. equation
\[\vecs{n}⋅\vecd{PQ}=0 \nonumber \]
inajulikana kama equation vector ya ndege.
Equation scalar ya ndege (wakati mwingine pia huitwa equation kiwango cha ndege) zenye uhakika\(P=(x_0,y_0,z_0)\) na vector kawaida\(\vec{n}=⟨a,b,c⟩\) ni
\[a(x−x_0)+b(y−y_0)+c(z−z_0)=0. \nonumber \]
Equation hii inaweza kuwa walionyesha kama\(ax+by+cz+d=0,\) ambapo Aina\(d=−ax_0−by_0−cz_0.\) hii ya equation wakati mwingine huitwa fomu ya jumla ya equation ya ndege.
Kama ilivyoelezwa hapo awali katika sehemu hii, pointi yoyote tatu ambazo sio zote ziko kwenye mstari huo huamua ndege. Kutokana na pointi tatu hizo, tunaweza kupata equation kwa ndege iliyo na pointi hizi.
Andika equation kwa ndege iliyo\(P=(1,1,−2), Q=(0,2,1),\) na pointi na\(R=(−1,−1,0)\) katika fomu zote mbili na za jumla.
Suluhisho
Kuandika equation kwa ndege, ni lazima kupata vector kawaida kwa ndege. Tunaanza kwa kutambua vectors mbili katika ndege:
\[ \begin{align*} \vecd{PQ} &=⟨0−1,2−1,1−(−2)⟩\\[4pt] &=⟨−1,1,3⟩ \\[4pt] \vecd{QR} &=⟨−1−0,−1−2,0−1⟩\\[4pt] &=⟨−1,−3,−1⟩.\end{align*}\]
Bidhaa ya msalaba\(\vecd{PQ}×\vecd{QR}\) ni orthogonal kwa wote\(\vecd{PQ}\) na\(\vecd{QR}\), hivyo ni kawaida kwa ndege ambayo ina vectors hizi mbili:
\[ \begin{align*} \vecs n &=\vecd{PQ}×\vecd{QR} \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\−1 & 1 & 3\\−1 & −3 & −1\end{vmatrix} \\[4pt] &=(−1+9)\mathbf{\hat i}−(1+3)\mathbf{\hat j}+(3+1)\mathbf{\hat k} \\[4pt] &= 8\mathbf{\hat i}−4\mathbf{\hat j}+4\mathbf{\hat k}.\end{align*}\]
Hivyo,\(\vecs n=⟨8,−4,4⟩,\) na tunaweza kuchagua yoyote ya pointi tatu kutolewa kuandika equation ya ndege:
\[ \begin{align*} 8(x−1)−4(y−1)+4(z+2) &=0 \\[4pt] 8x−4y+4z+4 &=0. \end{align*}\]
Ulinganisho wa scalar wa ndege hutofautiana kulingana na vector ya kawaida na hatua iliyochaguliwa.
Find equation ya ndege kwamba hupita katika hatua\((1,4,3)\) na ina line iliyotolewa na\(x=\dfrac{y−1}{2}=z+1.\)
Suluhisho
Ulinganifu wa usawa huelezea mstari unaopita kupitia hatua\((0,1,−1)\) inayofanana na vector\(\vecs v_1=⟨1,2,1⟩\) (angalia takwimu zifuatazo). Tumia hatua hii na hatua iliyotolewa,\((1,4,3),\) kutambua vector pili sambamba na ndege:
\[ \vecs v_2=⟨1−0,4−1,3−(−1)⟩=⟨1,3,4⟩. \nonumber \]
Tumia bidhaa ya msalaba wa wadudu hawa kutambua vector ya kawaida kwa ndege:
\[ \begin{align*} \vecs n &=\vecs v_1×\vecs v_2 \nonumber \\[4pt] &=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\1 & 2 & 1\\1 & 3 & 4\end{vmatrix} \nonumber \\[4pt] &=(8−3)\mathbf{\hat i}−(4−1)\mathbf{\hat j}+(3−2)\mathbf{\hat k} \\[4pt] &=5\mathbf{\hat i}−3\mathbf{\hat j}+\mathbf{\hat k}. \nonumber\end{align*}\]
Equations scalar kwa ndege ni\(5x−3(y−1)+(z+1)=0\) na\(5x−3y+z+4=0.\)
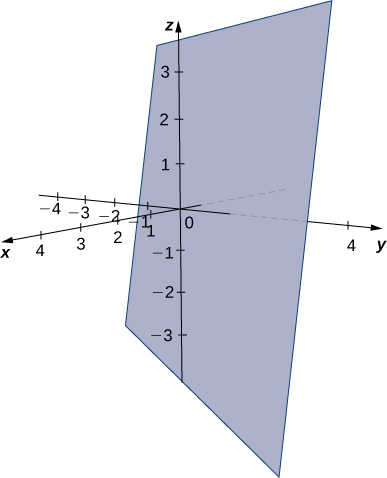
Kupata equation ya ndege zenye mistari\(L_1\) na\(L_2\):
\[ L_1: \; x=−y=z \nonumber \]
\[ L_2:\; \dfrac{x−3}{2}=y=z−2. \nonumber \]
- Kidokezo
-
Kidokezo: Bidhaa ya msalaba wa vectors ya mwelekeo wa mistari hutoa vector ya kawaida kwa ndege.
- Jibu
-
\[ −2(x−1)+(y+1)+3(z−1)=0 \nonumber \]
au
\[ −2x+y+3z=0 \nonumber \]
Sasa kwa kuwa tunaweza kuandika equation kwa ndege, tunaweza kutumia equation kupata umbali\(d\) kati ya uhakika\(P\) na ndege. Inafafanuliwa kama umbali mfupi iwezekanavyo kutoka\(P\) kwa uhakika kwenye ndege.
Kama tunavyopata umbali wa pande mbili kati ya hatua na mstari kwa kuhesabu urefu wa sehemu ya mstari perpendicular kwa mstari, tunapata umbali wa tatu-dimensional kati ya uhakika na ndege kwa kuhesabu urefu wa sehemu ya mstari perpendicular kwa ndege. Hebu\(R\) kuwa hatua katika ndege kama hiyo\(\vecd{RP}\) ni orthogonal kwa ndege, na hebu\(Q\) kuwa hatua ya kiholela katika ndege. Kisha makadirio ya vector\(\vecd{QP}\) kwenye vector kawaida inaelezea vector\(\vecd{RP}\), kama inavyoonekana katika Kielelezo\(\PageIndex{8}\).
Tuseme ndege yenye vector ya kawaida\(\vecs{n}\) hupita kupitia hatua\(Q\). Umbali\(d\) kutoka ndege hadi hatua\(P\) isiyo katika ndege hutolewa na
\[d=‖\text{proj}_\vecs{n}\,\vecd{QP}‖=∣\text{comp}_\vecs{n}\, \vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs{n}∣}{‖\vecs{n}‖}. \label{distanceplanepoint} \]
Kupata umbali kati ya uhakika\(P=(3,1,2)\) na ndege iliyotolewa na\(x−2y+z=5\) (angalia takwimu zifuatazo).
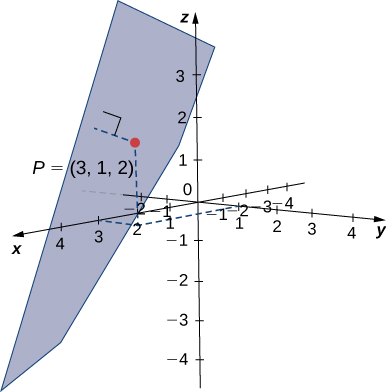
Suluhisho
Coefficients ya equation ya ndege hutoa vector kawaida kwa ndege:\(\vecs{n}=⟨1,−2,1⟩\). Ili kupata vector\(\vecd{QP}\), tunahitaji uhakika katika ndege. Hatua yoyote itafanya kazi, hivyo\(y=z=0\) kuweka kuona kwamba hatua\(Q=(5,0,0)\) iko katika ndege. Pata fomu ya sehemu ya vector kutoka\(Q\) kwa\(P\):
\[ \vecd{QP}=⟨3−5,1−0,2−0⟩=⟨−2,1,2⟩. \nonumber \]
Tumia formula ya umbali kutoka kwa Equation\ ref {distanceplanepoint}:
\[\begin{align*} d &=\dfrac{∣\vecd{QP}⋅\vecs n|}{‖\vecs n‖} \\[4pt] &=\dfrac{|⟨−2,1,2⟩⋅⟨1,−2,1⟩|}{\sqrt{1^2+(−2)^2+1^2}} \\[4pt] &=\dfrac{|−2−2+2|}{\sqrt{6}} \\[4pt] &=\dfrac{2}{\sqrt{6}} = \dfrac{\sqrt{6}}{3}\,\text{units}. \end{align*}\]
Kupata umbali kati ya uhakika\(P=(5,−1,0)\) na ndege iliyotolewa na\(4x+2y−z=3\).
- Kidokezo
-
Point\((0,0,−3)\) liko juu ya ndege.
- Jibu
-
\[ \dfrac{15}{\sqrt{21}} = \dfrac{5\sqrt{21}}{7}\,\text{units} \nonumber \]
Ndege Sambamba na Intersecting
Tumejadili mahusiano mbalimbali iwezekanavyo kati ya mistari miwili katika vipimo viwili na vipimo vitatu. Wakati sisi kuelezea uhusiano kati ya ndege mbili katika nafasi, tuna uwezekano mbili tu: ndege mbili tofauti ni sambamba au wao intersect. Wakati ndege mbili ni sambamba, vectors yao ya kawaida ni sawa. Wakati ndege mbili zinakabiliana, makutano ni mstari (Kielelezo\(\PageIndex{9}\)).
Tunaweza kutumia equations ya ndege mbili kupata equations parametric kwa mstari wa makutano.
Pata usawa wa parametric na ulinganifu kwa mstari uliofanywa na makutano ya ndege\(x+y+z=0\) zilizotolewa na\(2x−y+z=0\) (angalia takwimu zifuatazo).
Suluhisho
Kumbuka kuwa ndege mbili na normals nonparallel, hivyo ndege intersect. Zaidi ya hayo, asili inatimiza kila equation, kwa hiyo tunajua mstari wa makutano hupita kupitia asili. Kuongeza equations ndege ili tuweze kuondoa moja ya vigezo, katika kesi hii,\(y\):
\(x+y+z=0\)
\(2x−y+z=0\)
________________
\(3x+2z=0\).
Hii inatupa\(x=−\dfrac{2}{3}z.\) Sisi badala thamani hii katika equation kwanza kueleza\(y\) katika suala la\(z\):
\[ \begin{align*} x+y+z =0 \\[4pt] −\dfrac{2}{3}z+y+z =0 \\[4pt] y+\dfrac{1}{3}z =0 \\[4pt] y =−\dfrac{1}{3}z \end{align*}. \nonumber \]
Sasa tuna kwanza vigezo mbili,\(x\) na\(y\), katika suala la variable tatu,\(z\). Sasa tunafafanua\(z\) katika suala la\(t\). Ili kuondoa haja ya sehemu ndogo, tunachagua kufafanua parameter\(t\) kama\(t=−\dfrac{1}{3}z\). Kisha,\(z=−3t\). Kubadilisha uwakilishi wa parametric wa\(z\) nyuma katika equations nyingine mbili, tunaona kwamba equations parametric kwa mstari wa makutano ni\(x=2t, \; y=t, \; z=−3t.\) equations symmetric kwa mstari ni\(\dfrac{x}{2}=y=\dfrac{z}{−3}\).
Pata usawa wa parametric kwa mstari uliofanywa na makutano ya ndege\(x+y−z=3\) na\(3x−y+3z=5.\)
- Kidokezo
-
Ongeza equations mbili, kisha ueleze\(z\) katika suala la\(x\). Kisha, kueleza\(y\) katika suala la\(x\).
- Jibu
-
\( x=t, \; y=7−3t,\; z=4−2t\)
Mbali na kutafuta equation ya mstari wa makutano kati ya ndege mbili, tunaweza kuhitaji kupata angle iliyoundwa na makutano ya ndege mbili. Kwa mfano, wajenzi kujenga nyumba wanahitaji kujua angle ambapo sehemu tofauti za paa hukutana ili kujua kama paa itaonekana vizuri na kukimbia vizuri. Tunaweza kutumia vectors kawaida kuhesabu angle kati ya ndege mbili. Tunaweza kufanya hivyo kwa sababu angle kati ya wadudu wa kawaida ni sawa na angle kati ya ndege. Kielelezo\(\PageIndex{10}\) kinaonyesha kwa nini hii ni kweli.
Tunaweza kupata kipimo cha angle\(θ\) kati ya ndege mbili za kuingiliana kwa kwanza kutafuta cosine ya angle, kwa kutumia equation ifuatayo:
\[\cos θ=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖}. \nonumber \]
Basi tunaweza kutumia angle kuamua kama ndege mbili ni sambamba au orthogonal au kama wao intersect katika pembe nyingine.
Kuamua kama kila jozi ya ndege ni sambamba, orthogonal, au wala. Ikiwa ndege zinaingiliana, lakini sio orthogonal, pata kipimo cha angle kati yao. Kutoa jibu kwa radians na pande zote kwa maeneo mawili ya decimal.
- \(x+2y−z=8\)na\(2x+4y−2z=10\)
- \(2x−3y+2z=3\)na\(6x+2y−3z=1\)
- \(x+y+z=4\)na\(x−3y+5z=1\)
Suluhisho:
- Vectors kawaida kwa ndege hizi ni\(\vecs{n}_1=⟨1,2,−1⟩\) na\(\vecs{n}_2=⟨2,4,−2⟩.\) wadudu hawa wawili ni mizigo scalar ya kila mmoja. Vectors kawaida ni sambamba, hivyo ndege ni sambamba.
- Vectors kawaida kwa ndege hizi ni\(\vecs{n}_1=⟨2,−3,2⟩\) na\(\vecs{n}_2=⟨6,2,−3⟩\). Kuchukua bidhaa dot ya wadudu hawa, tuna\[\begin{align*} \vecs{n}_1⋅\vecs{n}_2 =⟨2,−3,2⟩⋅⟨6,2,−3⟩\\[4pt] =2(6)−3(2)+2(−3)=0.\end{align*} \nonumber \] wadudu kawaida ni orthogonal, hivyo ndege sambamba ni orthogonal pia.
- wadudu kawaida kwa ndege hizi ni\(\vecs n_1=⟨1,1,1⟩\) na\(\vecs n_2=⟨1,−3,5⟩\):\[\begin{align*} \cos θ &=\dfrac{|\vecs{n}_1⋅\vecs{n}_2|}{‖\vecs{n}_1‖‖\vecs{n}_2‖} \\[4pt] &=\dfrac{|⟨1,1,1⟩⋅⟨1,−3,5⟩|}{\sqrt{1^2+1^2+1^2}\sqrt{1^2+(−3)^2+5^2}} \\[4pt] &=\dfrac{3}{\sqrt{105}} \end{align*}\]
kisha\(\theta =\arccos {\frac{3}{\sqrt{105}}} \approx 1.27\) rad.
Hivyo angle kati ya ndege mbili ni kuhusu\(1.27\) rad, au takriban\(73°\).
Kupata kipimo cha angle kati ya ndege\(x+y−z=3\) na\(3x−y+3z=5.\) Kutoa jibu katika radians na pande zote kwa sehemu mbili decimal.
- Kidokezo
-
Matumizi coefficients ya vigezo katika kila equation kupata vector kawaida kwa kila ndege.
- Jibu
-
\( 1.44\, \text{rad} \)
Tunapopata kwamba ndege mbili ni sambamba, tunaweza kuhitaji kupata umbali kati yao. Ili kupata umbali huu, tunachagua tu hatua katika moja ya ndege. Umbali kutoka hatua hii hadi ndege nyingine ni umbali kati ya ndege.
Hapo awali, tulianzisha formula ya kuhesabu umbali huu katika Equation\ ref {distanceplanepoint}:
\[d=\dfrac{\vecd{QP}⋅\vecs{n}}{‖\vecs{n}‖}, \nonumber \]
ambapo\(Q\) ni uhakika juu ya ndege,\(P\) ni hatua si kwenye ndege, na\(\vec{n}\) ni vector kawaida kwamba hupitia hatua\(Q\). Fikiria umbali kutoka hatua\((x_0,y_0,z_0)\) hadi ndege\(ax+by+cz+k=0.\) Hebu\((x_1,y_1,z_1)\) iwe na uhakika wowote katika ndege. Kubadilisha katika mazao ya formula
\[\begin{align*}d =\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|}{\sqrt{a^2+b^2+c^2}} \\[4pt] =\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}.\end{align*}\]
Tunasema matokeo haya rasmi katika theorem ifuatayo.
Hebu\(P(x_0,y_0,z_0)\) kuwa hatua. Umbali kutoka\(P\) kwa ndege\(ax+by+cz+k=0\) hutolewa na
\[d=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}}. \nonumber \]
Find umbali kati ya ndege mbili sambamba iliyotolewa\(2x+y−z=2\) na\(2x+y−z=8.\)
Suluhisho
Point\((1,0,0)\) iko katika ndege ya kwanza. Umbali uliotaka, basi, ni
\[\begin{align*} d &=\dfrac{|ax_0+by_0+cz_0+k|}{\sqrt{a^2+b^2+c^2}} \\[4pt] &= \dfrac{|2(1)+1(0)+(−1)(0)+(−8)|}{\sqrt{2^2+1^2+(−1)^2}} \\[4pt] &= \dfrac{6}{\sqrt{6}}=\sqrt{6} \,\text{units} \end{align*}\]
Kupata umbali kati ya ndege sambamba\(5x−2y+z=6\) na\(5x−2y+z=−3\).
- Kidokezo
-
Weka\(x=y=0\) ili kupata uhakika kwenye ndege ya kwanza.
- Jibu
-
\(\dfrac{9}{\sqrt{30}} = \dfrac{3\sqrt{30}}{10}\,\text{units} \)
Kupata umbali kutoka hatua hadi mstari au kutoka mstari hadi ndege inaonekana kama utaratibu mzuri wa abstract. Lakini, kama mistari inawakilisha mabomba katika mmea wa kemikali au zilizopo katika kusafishia mafuta au barabara katika makutano ya barabara, kuthibitisha kuwa umbali kati yao hukutana na specifikationer inaweza kuwa muhimu na Awkward kupima. Njia moja ni kutengeneza mabomba mawili kama mistari, kwa kutumia mbinu katika sura hii, na kisha uhesabu umbali kati yao. Mahesabu inahusisha kutengeneza vectors kando ya maelekezo ya mistari na kutumia bidhaa zote za msalaba na bidhaa ya dot.
Aina za ulinganifu wa mistari miwili,\(L_1\) na\(L_2\), ni
\[L_1:\dfrac{x−x_1}{a_1}=\dfrac{y−y_1}{b_1}=\dfrac{z−z_1}{c_1} \nonumber \]
\[L_2:\dfrac{x−x_2}{a_2}=\dfrac{y−y_2}{b_2}=\dfrac{z−z_2}{c_2}. \nonumber \]
Wewe ni kuendeleza formula kwa umbali\(d\) kati ya mistari hii miwili, kwa suala la maadili\(a_1,b_1,c_1;a_2,b_2,c_2;x_1,y_1,z_1;\) na umbali kati\(x_2,y_2,z_2.\) ya mistari miwili ni kawaida kuchukuliwa kwa maana ya umbali wa chini, hivyo hii ni urefu wa sehemu ya mstari au urefu wa vector ambayo ni perpendicular kwa mistari yote na intersects mistari yote.
1. Kwanza, weka vectors mbili,\(\vecs{v}_1\) na\(\vecs{v}_2\), kwamba uongo pamoja\(L_1\) na\(L_2\), kwa mtiririko huo.
2. Pata bidhaa ya msalaba wa wadudu hawa wawili na kuiita\(\vecs{N}\). Vector hii ni perpendicular\(\vecs{v}_1\) na\(\vecs{v}_2\), na hivyo ni perpendicular kwa mistari yote.
3. Kutoka vector\(\vecs{N}\), fanya vector kitengo\(\vecs{n}\) katika mwelekeo huo.
4. Tumia equations ya ulinganifu ili kupata vector rahisi\(\vecs{v}_{12}\) ambayo iko kati ya pointi mbili, moja kwenye kila mstari. Tena, hii inaweza kufanyika moja kwa moja kutoka kwa usawa wa usawa.
5. Bidhaa ya dot ya vectors mbili ni ukubwa wa makadirio ya vector moja kwenye nyingine-yaani,\(\vecs A⋅\vecs B=‖\vecs{A}‖‖\vecs{B}‖\cos θ,\) wapi\(θ\) pembe kati ya vectors. Kutumia bidhaa dot, kupata makadirio ya vector\(\vecs{v}_{12}\) kupatikana katika hatua\(4\) kwenye kitengo vector\(\vecs{n}\) kupatikana katika hatua\(3\). Makadirio haya ni perpendicular kwa mistari yote, na hivyo urefu wake lazima umbali perpendicular d kati yao. Kumbuka kuwa thamani ya\(d\) inaweza kuwa hasi, kulingana na uchaguzi wako wa vector\(\vecs{v}_{12}\) au utaratibu wa bidhaa msalaba, kwa hiyo tumia ishara za thamani kamili karibu na namba.
6. Angalia kwamba formula yako inatoa umbali sahihi wa\(|−25|/\sqrt{198}≈1.78\) kati ya mistari miwili ifuatayo:
\[L_1:\dfrac{x−5}{2}=\dfrac{y−3}{4}=\dfrac{z−1}{3} \nonumber \]
\[L_2:\dfrac{x−6}{3}=\dfrac{y−1}{5}=\dfrac{z}{7}. \nonumber \]
7. Je kujieleza yako kwa ujumla halali wakati mistari ni sambamba? Ikiwa sio, kwa nini? (Kidokezo: Unajua nini kuhusu thamani ya bidhaa msalaba wa vectors mbili sambamba? Matokeo hayo yangeonekana wapi katika kujieleza kwako kwa\(d\)?)
8. Onyesha kwamba maneno yako kwa umbali ni sifuri wakati mistari inapoingiliana. Kumbuka kwamba mistari miwili inaingiliana ikiwa sio sambamba na iko katika ndege moja. Kwa hiyo, fikiria mwelekeo wa\(\vecs{n}\) na\(\vecs{v}_{12}\). Matokeo ya bidhaa zao za dot ni nini?
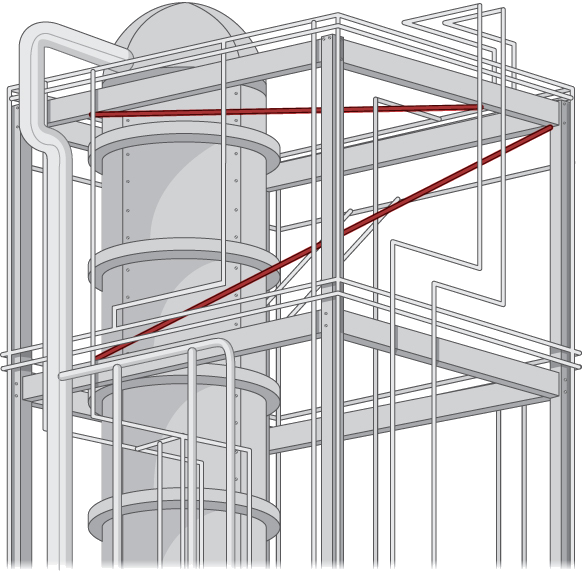
9. Fikiria maombi yafuatayo. Wahandisi katika kusafishia wameamua wanahitaji kufunga vipande vya msaada kati ya mabomba mengi ya gesi ili kupunguza vibrations vya kuharibu. Ili kupunguza gharama, wanapanga kufunga vipande hivi kwenye pointi za karibu kati ya mabomba yaliyo karibu. Kwa sababu wana schematics ya kina ya muundo, wana uwezo wa kuamua urefu sahihi wa vipande vinavyohitajika, na hivyo kutengeneza na kusambaza kwa wafanyakazi wa ufungaji bila kutumia muda wa thamani kufanya vipimo.
Muundo wa sura ya mstatili una vipimo\(4.0×15.0×10.0\,\text{m}\) (urefu, upana, na kina). Sekta moja ina bomba inayoingia kona ya chini ya kitengo cha sura ya kawaida na ikitoka kwenye kona iliyopinga kinyume (moja mbali zaidi juu); piga simu hii\(L_1\). Bomba la pili linaingia na hutoka kwenye pembe mbili tofauti za chini; piga simu hii\(L_2\) (Kielelezo\(\PageIndex{12}\)).
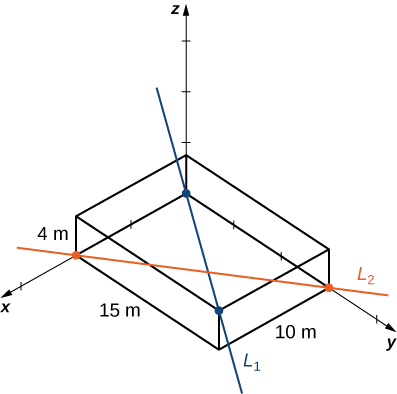
Andika wadudu kwenye mistari inayowakilisha mabomba hayo, pata bidhaa ya msalaba kati yao ambayo unaweza kuunda vector ya kitengo\(\vecs n\), kufafanua vector inayozunguka pointi mbili kwenye kila mstari, na hatimaye kuamua umbali wa chini kati ya mistari. (Chukua asili kuwa kwenye kona ya chini ya bomba la kwanza.) Vile vile, unaweza pia kuendeleza equations symmetric kwa kila mstari na mbadala moja kwa moja katika formula yako.
Dhana muhimu
- Katika vipimo vitatu, mwelekeo wa mstari unaelezewa na vector ya mwelekeo. equation vector ya mstari na mwelekeo vector\(\vecs v=⟨a,b,c⟩\) kupitia hatua\(P=(x_0,y_0,z_0)\) ni\(\vecs r=\vecs r_0+t\vecs v\), wapi\(\vecs r_0=⟨x_0,y_0,z_0⟩\) msimamo vector ya uhakika\(P\). Equation hii inaweza kuandikwa upya ili kuunda equations parametric ya mstari:\(x=x_0+ta,y=y_0+tb\), na\(z=z_0+tc\). Mstari unaweza pia kuelezewa na equations ya ulinganifu\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\).
- Hebu\(L\) kuwa mstari katika nafasi inayopitia hatua\(P\) na vector mwelekeo\(\vecs v\). Kama\(Q\) ni hatua yoyote si juu\(L\), basi umbali kutoka\(Q\) kwa\(L\) ni\(d=\dfrac{‖\vecd{PQ}×\vecs v‖}{‖\vecs v‖}.\)
- Katika vipimo vitatu, mistari miwili inaweza kuwa sambamba lakini si sawa, sawa, intersecting, au skew.
- Kutokana na uhakika\(P\) na vector\(\vecs n\), seti ya pointi zote\(Q\) kuridhisha equation\(\vecs n⋅\vecd{PQ}=0\) aina ndege. Equation\(\vecs n⋅\vecd{PQ}=0\) inajulikana kama equation vector ya ndege.
- equation scalar ya ndege zenye uhakika\(P=(x_0,y_0,z_0)\) na vector kawaida\(\vecs n=⟨a,b,c⟩\) ni\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\). Equation hii inaweza kuwa walionyesha kama\(ax+by+cz+d=0,\) ambapo Aina\(d=−ax_0−by_0−cz_0.\) hii ya equation wakati mwingine huitwa fomu ya jumla ya equation ya ndege.
- Tuseme ndege yenye vector ya kawaida\(n\) hupita kupitia hatua\(Q\). Umbali\(D\) kutoka ndege kwa uhakika\(P\) si katika ndege hutolewa na
\[D=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vec{QP}∣=\dfrac{∣\vec{QP}⋅\vecs n∣}{‖\vecs n‖.} \nonumber \]
- Vectors kawaida ya ndege sambamba ni sambamba. Wakati ndege mbili zinakabiliana, zinaunda mstari.
- Kipimo cha angle\(θ\) kati ya ndege mbili za kuingiliana kinaweza kupatikana kwa kutumia equation:\(\cos θ=\dfrac{|\vecs{n}_1⋅\vecs n_2|}{‖\vecs n_1‖‖\vecs n_2‖}\), wapi\(\vecs n_1\) na\(\vecs n_2\) ni wadudu wa kawaida kwa ndege.
- Umbali\(D\) kutoka hatua\((x_0,y_0,z_0)\) hadi ndege\(ax+by+cz+d=0\) hutolewa na
\[D=\dfrac{|a(x_0−x_1)+b(y_0−y_1)+c(z_0−z_1)|} {\sqrt{a^2+b^2+c^2}}=\dfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \nonumber \].
Mlinganyo muhimu
- Vector equation ya mstari
\(\vecs r=\vecs r_0+t\vecs v\)
- Ulinganisho wa parametric wa Mstari
\(x=x_0+ta,\; y=y_0+tb,\)na\(z=z_0+tc\)
- Ulinganifu wa Ulinganifu wa Mstari
\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\)
- Vector equation ya ndege
\(\vecs n⋅\vecd{PQ}=0\)
- Mlinganyo wa Scalar wa Ndege
\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\)
- Umbali kati ya Ndege na Point
\(d=‖\text{proj}_\vecs{n}\vecd{QP}‖=∣\text{comp}_\vecs{n}\vecd{QP}∣=\dfrac{∣\vecd{QP}⋅\vecs n∣}{‖\vecs n‖}\)
faharasa
- mwelekeo vector
- vector sambamba na mstari ambayo hutumiwa kuelezea mwelekeo, au mwelekeo, wa mstari katika nafasi
- fomu ya jumla ya equation ya ndege
- equation katika fomu\(ax+by+cz+d=0,\) ambapo\(\vecs n=⟨a,b,c⟩\) ni vector kawaida ya ndege,\(P=(x_0,y_0,z_0)\) ni hatua juu ya ndege, na\(d=−ax_0−by_0−cz_0\)
- vector ya kawaida
- vector perpendicular kwa ndege
- equations parametric ya mstari
- seti ya equations\(x=x_0+ta, y=y_0+tb,\) na\(z=z_0+tc\) kuelezea mstari na vector mwelekeo\(v=⟨a,b,c⟩\) kupitia hatua\((x_0,y_0,z_0)\)
- equation scalar ya ndege
- equation\(a(x−x_0)+b(y−y_0)+c(z−z_0)=0\) kutumika kuelezea ndege zenye uhakika\(P=(x_0,y_0,z_0)\) na vector kawaida\(n=⟨a,b,c⟩\) au fomu yake mbadala\(ax+by+cz+d=0\), wapi\(d=−ax_0−by_0−cz_0\)
- skew mistari
- mistari miwili ambayo si sambamba lakini si intersect
- equations symmetric ya mstari
- equations\(\dfrac{x−x_0}{a}=\dfrac{y−y_0}{b}=\dfrac{z−z_0}{c}\) kuelezea mstari na mwelekeo vector\(v=⟨a,b,c⟩\) kupitia hatua\((x_0,y_0,z_0)\)
- vector equation ya mstari
- equation\(\vecs r=\vecs r_0+t\vecs v\) kutumika kuelezea mstari na mwelekeo vector\(\vecs v=⟨a,b,c⟩\) kupitia hatua\(P=(x_0,y_0,z_0)\), ambapo\(\vecs r_0=⟨x_0,y_0,z_0⟩\), ni nafasi vector ya uhakika\(P\)
- vector equation ya ndege
- equation\(\vecs n⋅\vecd{PQ}=0,\) ambapo\(P\) ni hatua fulani katika ndege,\(Q\) ni hatua yoyote katika ndege, na\(\vecs n\) ni vector kawaida ya ndege


