12.2: Vectors katika Vipimo Tatu
- Page ID
- 178064
- Eleza nafasi tatu-dimensional hesabu.
- Pata pointi katika nafasi kwa kutumia kuratibu.
- Andika formula ya umbali katika vipimo vitatu.
- Andika equations kwa ndege rahisi na nyanja.
- Kufanya shughuli vector katika\(\mathbb{R}^{3}\).
Vectors ni zana muhimu za kutatua matatizo mbili-dimensional. Maisha, hata hivyo, hutokea kwa vipimo vitatu. Ili kupanua matumizi ya vectors kwa maombi ya kweli zaidi, ni muhimu kuunda mfumo wa kuelezea nafasi tatu-dimensional. Kwa mfano, ingawa ramani mbili-dimensional ni chombo muhimu cha kusafiri kutoka sehemu moja hadi nyingine, wakati mwingine uchapaji wa ardhi ni muhimu. Je, njia yako iliyopangwa inapita kupitia milima? Je! Unahitaji kuvuka mto? Ili kufahamu kikamilifu athari za vipengele hivi vya kijiografia, lazima utumie vipimo vitatu. Sehemu hii inatoa ugani wa asili wa ndege ya kuratibu ya Cartesian mbili-dimensional katika vipimo vitatu.
Mifumo ya Kuratibu Tatu
Kama tulivyojifunza, mfumo wa kuratibu mstatili wa mstatili una safu mbili za perpendicular: usawa\(x\) -axis na wima \(y\)-axis. Tunaweza kuongeza mwelekeo wa tatu,\(z\) -axis, ambayo ni perpendicular kwa wote\(x\) -axis na\(y\) -axis. Tunaita mfumo huu mfumo wa kuratibu mstatili wa mstatili wa tatu. Inawakilisha vipimo vitatu tunavyokutana katika maisha halisi.
Mfumo wa kuratibu mstatili wa mstatili una safu tatu za perpendicular:\(x\)\(y\) -axis, -axis, na\(z\) -axis. Kwa sababu kila mhimili ni namba line anayewakilisha namba zote halisi katika\(ℝ\), mfumo tatu-dimensional ni mara nyingi ulionyehsa na\(ℝ^3\).
Katika Mchoro\(\PageIndex{1a}\), \(z\)mhimili mzuri unaonyeshwa juu ya ndege iliyo na\(x\) - na\(y\) -axes. \(x\)Mhimili mzuri unaonekana upande wa kushoto na\(y\) mhimili mzuri ni wa kulia. Swali la asili la kuuliza ni: Mpangilio huu uliamuaje? Mfumo unaonyeshwa unafuata utawala wa mkono wa kulia. Ikiwa tunachukua mkono wetu wa kulia na kuunganisha vidole na\(x\) mhimili mzuri, kisha curl vidole ili waweze kuelekeza katika mwelekeo wa \(y\)-axis chanya, pointi zetu za kidole katika mwelekeo wa chanya\(z\) -axis (Kielelezo\(\PageIndex{1b}\)). Katika maandishi haya, sisi daima tunafanya kazi na mifumo ya kuratibu iliyoanzishwa kwa mujibu wa utawala wa mkono wa kulia. Mifumo mingine hufuata utawala wa mkono wa kushoto, lakini utawala wa mkono wa kulia unachukuliwa kuwa uwakilishi wa kawaida.
Katika vipimo viwili, tunaelezea hatua katika ndege na kuratibu\((x,y)\). Kila kuratibu inaelezea jinsi hatua inavyofanana na mhimili unaofanana. Katika vipimo vitatu, kuratibu mpya\(z\), imeongezwa ili kuonyesha usawa na\(z\) -axis:\((x,y,z)\). Hatua katika nafasi ni kutambuliwa na kuratibu zote tatu (Kielelezo\(\PageIndex{2}\)). Ili kupanga njama\((x,y,z)\), nenda\(x\) vitengo kando ya \(x\)mhimili, kisha \(y\)vitengo katika mwelekeo wa\(y\) -axis, kisha\(z\) vitengo katika mwelekeo wa\(z\) -axis.
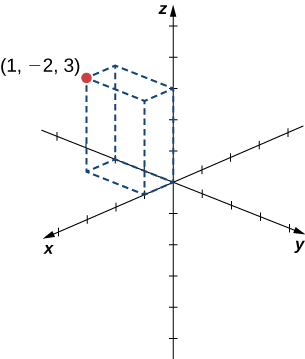
Piga hatua\((1,−2,3)\) katika nafasi tatu-dimensional.
Suluhisho
Ili kuchora hatua, kuanza kwa sketching pande tatu za mche mstatili pamoja na shoka za kuratibu: kitengo kimoja katika\(x\) mwelekeo mzuri,\(2\) vitengo katika\(y\) mwelekeo hasi, na\(3\) vitengo katika\(z\) mwelekeo mzuri. Jaza mche ili kupanga njama (Kielelezo\(\PageIndex{3}\)).
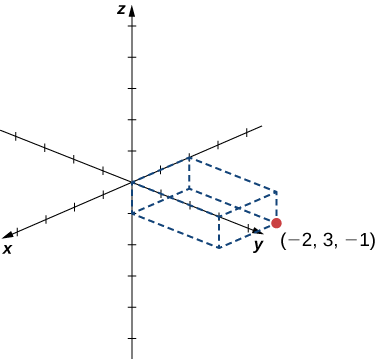
Piga hatua\((−2,3,−1)\) katika nafasi tatu-dimensional.
- Kidokezo
-
Anza kwa sketching shoka kuratibu. kwa mfano, Kielelezo\(\PageIndex{3}\). Kisha mchoro mchele wa mstatili ili kusaidia kupata uhakika katika nafasi.
- Jibu
-
Katika nafasi mbili-dimensional, ndege ya kuratibu inaelezwa na jozi ya axes perpendicular. Axes hizi zinatuwezesha kutaja eneo lolote ndani ya ndege. Katika vipimo vitatu, tunafafanua ndege za kuratibu na safu za kuratibu, kama vile katika vipimo viwili. Kuna axes tatu sasa, kwa hiyo kuna jozi tatu za kuingiliana za axes. Kila jozi ya axes huunda ndege ya kuratibu:\(xy\) -ndege, \(xz\)-ndege, na\(yz\) -ndege (Kielelezo\(\PageIndex{4}\)). Sisi kufafanua\(xy\) -ndege rasmi kama kuweka zifuatazo:\(\{(x,y,0):x,y∈ℝ\}.\) Vile vile, \(xz\)-ndege na\(yz\) -ndege hufafanuliwa kama\(\{(x,0,z):x,z∈ℝ\}\) na\(\{(0,y,z):y,z∈ℝ\},\) kwa mtiririko huo.
Kwa taswira hii, fikiria wewe ni kujenga nyumba na wamesimama katika chumba na mbili tu ya kuta nne kumaliza. (Kudhani mbili kumaliza kuta ni karibu na kila mmoja.) Ikiwa unasimama na nyuma yako kwenye kona ambapo kuta mbili za kumaliza zinakutana, zinakabiliwa ndani ya chumba, sakafu ni\(xy\) -ndege, ukuta wa kulia wako ni \(xz\)ndege, na ukuta upande wa kushoto wako ni \(yz\)ndege.
Katika vipimo viwili, safu za kuratibu zinagawanya ndege katika quadrants nne. Vile vile, ndege za kuratibu zinagawanya nafasi kati yao katika mikoa nane kuhusu asili, inayoitwa octants. Octants kujaza\(ℝ^3\) kwa njia ile ile ambayo quadrants kujaza\(ℝ^2\), kama inavyoonekana katika Kielelezo\(\PageIndex{5}\).
Wengi hufanya kazi katika nafasi tatu-dimensional ni ugani wa starehe wa dhana zinazofanana katika vipimo viwili. Katika sehemu hii, tunatumia ujuzi wetu wa miduara kuelezea nyanja, kisha tunapanua ufahamu wetu wa vectors kwa vipimo vitatu. Ili kukamilisha malengo haya, tunaanza kwa kurekebisha formula ya umbali kwa nafasi tatu-dimensional.
Ikiwa pointi mbili ziko katika ndege moja ya kuratibu, basi ni moja kwa moja kuhesabu umbali kati yao. Tunajua kwamba umbali\(d\) kati ya pointi mbili\((x_1,y_1)\) na\((x_2,y_2)\) katika ndege ya\(xy\) kuratibu hutolewa na formula
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Fomu ya umbali kati ya pointi mbili katika nafasi ni ugani wa asili wa formula hii.
Umbali\(d\) kati ya pointi\((x_1,y_1,z_1)\) na\((x_2,y_2,z_2)\) hutolewa na formula
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}. \label{distanceForm} \]
Ushahidi wa theorem hii umesalia kama zoezi. (Kidokezo: Kwanza kupata umbali\(d_1\) kati ya pointi\((x_1,y_1,z_1)\) na\((x_2,y_2,z_1)\) kama inavyoonekana katika Kielelezo\(\PageIndex{6}\).)
Pata umbali kati ya pointi\(P_1=(3,−1,5)\) na\(P_2=(2,1,−1).\)
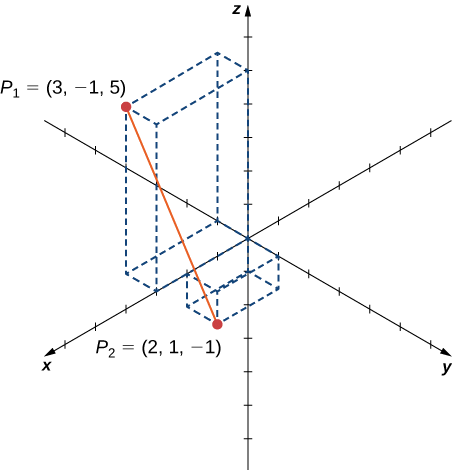
Suluhisho
Maadili ya mbadala moja kwa moja kwenye formula ya umbali (Equation\ ref {distanceForm}):
\[\begin{align*} d(P_1,P_2) &=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \\[4pt] &=\sqrt{(2−3)^2+(1−(−1))^2+(−1−5)^2} \\[4pt] &=\sqrt{(-1)^2+2^2+(−6)^2} \\[4pt] &=\sqrt{41}. \end{align*}\]
Kupata umbali kati ya pointi\(P_1=(1,−5,4)\) na\(P_2=(4,−1,−1)\).
- Kidokezo
-
\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}\)
- Jibu
-
\(5\sqrt{2}\)
Kabla ya kuhamia kwenye sehemu inayofuata, hebu tujisikie jinsi\(ℝ^3\) inatofautiana na\(ℝ^2\). Kwa mfano, katika\(ℝ^2\), mistari ambayo si sambamba lazima daima intersect. Hii si kesi katika\(ℝ^3\). Kwa mfano, fikiria mistari iliyoonyeshwa kwenye Kielelezo\(\PageIndex{8}\). Mstari huu wawili haufanani, wala hawapatikani.
Kielelezo\(\PageIndex{8}\): Mstari huu wawili haufanani, lakini bado hauingiliani.
Unaweza pia kuwa na duru ambazo zinaunganishwa lakini hazina pointi kwa pamoja, kama katika Kielelezo\(\PageIndex{9}\).
Kielelezo\(\PageIndex{9}\): Duru hizi zinaunganishwa, lakini hazina pointi sawa.
Tuna kubadilika zaidi kufanya kazi katika vipimo vitatu kuliko sisi kufanya kama sisi kukwama na vipimo viwili tu.
Kuandika equations katika\(ℝ^3\)
Sasa kwa kuwa tunaweza kuwakilisha pointi katika nafasi na kupata umbali kati yao, tunaweza kujifunza jinsi ya kuandika milinganyo ya vitu vya kijiometri kama vile mistari, ndege, na nyuso zilizopigwa ndani\(ℝ^3\). Kwanza, tunaanza na equation rahisi. Linganisha grafu ya equation\(x=0\) katika\(ℝ\),\(ℝ^2\), na\(ℝ^3\) (Kielelezo\(\PageIndex{10}\)). Kutoka grafu hizi, tunaweza kuona equation huo unaweza kuelezea uhakika, mstari, au ndege.
Katika nafasi, equation\(x=0\) inaelezea pointi zote\((0,y,z)\). Equation hii amefafanua\(yz\) -ndege. Vile vile,\(xy\) -ndege ina pointi zote za fomu\((x,y,0)\). Equation\(z=0\) inafafanua \(xy\)-ndege na equation\(y=0\) inaelezea\(xz\) -ndege (Kielelezo\(\PageIndex{11}\)).
Kuelewa equations ya ndege kuratibu inatuwezesha kuandika equation kwa ndege yoyote ambayo ni sambamba na moja ya ndege kuratibu. Wakati ndege ni sawa na \(xy\)-ndege, kwa mfano, kuratibu ya kila hatua katika ndege ina thamani sawa ya mara kwa mara.\(z\) Tu\(x\) - na \(y\)- kuratibu ya pointi katika ndege kwamba kutofautiana kutoka hatua kwa uhakika.
- Ndege katika nafasi ambayo ni sambamba na\(xy\) -ndege na ina uhakika\((a,b,c)\) inaweza kuwakilishwa na equation\(z=c\).
- Ndege katika nafasi ambayo ni sambamba na\(xz\) -ndege na ina uhakika\((a,b,c)\) inaweza kuwakilishwa na equation\(y=b\).
- Ndege katika nafasi ambayo ni sambamba na\(yz\) -ndege na ina uhakika\((a,b,c)\) inaweza kuwakilishwa na equation\(x=a\).
- Andika equation ya ndege kupita kwa njia ya uhakika\((3,11,7)\) kwamba ni sambamba na\(yz\) -plane.
- Find equation ya ndege kupita kwa njia ya pointi\((6,−2,9), (0,−2,4),\) na\((1,−2,−3).\)
Suluhisho
- Wakati ndege ni sambamba na\(yz\) -ndege, tu \(y\)- na\(z\) -kuratibu inaweza kutofautiana. \(x\)Kuratibu ina thamani sawa ya mara kwa mara kwa pointi zote katika ndege hii, hivyo ndege hii inaweza kuwakilishwa na equation\(x=3\).
- Kila moja ya pointi\((6,−2,9), (0,−2,4),\) na\((1,−2,−3)\) ina sawa \(y\)- kuratibu. Ndege hii inaweza kuwakilishwa na equation\(y=−2\).
Andika equation ya ndege kupita kwa njia ya uhakika\((1,−6,−4)\) kwamba ni sambamba na\(xy\) -plane.
- Kidokezo
-
Kama ndege ni sambamba na\(xy\) -ndege, z-kuratibu ya pointi katika ndege hiyo hazitofautiana.
- Jibu
-
\(z=−4\)
Kama tulivyoona,\(ℝ^2\) katika equation\(x=5\) inaelezea mstari wima kupitia hatua\((5,0)\). Mstari huu ni sawa na\(y\) -axis. Katika ugani wa asili, equation\(x=5\) in\(ℝ^3\) inaelezea ndege kupita katika hatua\((5,0,0)\), ambayo ni sambamba na \(yz\)-ndege. Ugani mwingine wa asili wa equation inayojulikana hupatikana katika usawa wa nyanja.
Tufe ni seti ya pointi zote katika nafasi equidistant kutoka hatua ya kudumu, katikati ya nyanja (Kielelezo\(\PageIndex{12}\)), kama seti ya pointi zote katika ndege ambayo ni equidistant kutoka katikati inawakilisha mduara. Katika nyanja, kama katika mduara, umbali kutoka katikati hadi hatua kwenye nyanja huitwa radius.
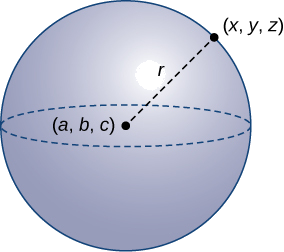
Ulinganisho wa mduara unatokana kwa kutumia formula ya umbali katika vipimo viwili. Kwa njia hiyo hiyo, equation ya nyanja inategemea formula tatu-dimensional kwa umbali.
Sifa na kituo\((a,b,c)\) na radius\(r\) inaweza kuwakilishwa na equation
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
Equation hii inajulikana kama equation ya kawaida ya nyanja.
Pata usawa wa kiwango cha nyanja na kituo\((10,7,4)\) na uhakika\((−1,3,−2)\), kama inavyoonekana kwenye Kielelezo\(\PageIndex{13}\).
Kielelezo\(\PageIndex{13}\): nyanja unaozingatia katika hatua\((10,7,4)\) zenye\((−1,3,−2).\)
Suluhisho
Tumia formula ya umbali ili kupata radius\(r\) ya nyanja:
\[\begin{align*} r &=\sqrt{(−1−10)^2+(3−7)^2+(−2−4)^2} \\[4pt] &=\sqrt{(−11)^2+(−4)^2+(−6)^2} \\[4pt] &=\sqrt{173} \end{align*} \nonumber \]
Equation ya kiwango cha nyanja ni
\[(x−10)^2+(y−7)^2+(z−4)^2=173. \nonumber \]
Pata usawa wa kiwango cha nyanja na kituo cha kituo\((−2,4,−5)\) kilicho na uhakika\((4,4,−1).\)
- Kidokezo
-
Kwanza tumia formula ya umbali ili kupata radius ya nyanja.
- Jibu
-
\[(x+2)^2+(y−4)^2+(z+5)^2=52 \nonumber \]
Hebu\(P=(−5,2,3)\) na\(Q=(3,4,−1)\), na tuseme sehemu ya mstari\(\overline{PQ}\) huunda kipenyo cha nyanja (Kielelezo\(\PageIndex{14}\)). Pata equation ya nyanja.
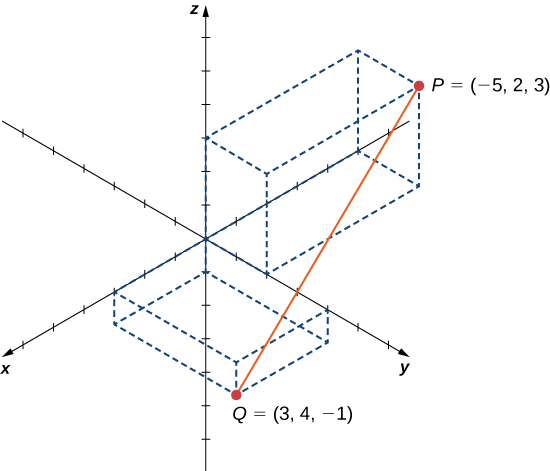
Suluhisho:
Kwa kuwa\(\overline{PQ}\) ni kipenyo cha nyanja, tunajua katikati ya nyanja ni midpoint\(\overline{PQ}\) ya.Kisha,
\[C=\left(\dfrac{−5+3}{2},\dfrac{2+4}{2},\dfrac{3+(−1)}{2}\right)=(−1,3,1). \nonumber \]
Zaidi ya hayo, tunajua Radius ya nyanja ni nusu urefu wa kipenyo. Hii inatoa
\[\begin{align*} r &=\dfrac{1}{2}\sqrt{(−5−3)^2+(2−4)^2+(3−(−1))^2} \\[4pt] &=\dfrac{1}{2}\sqrt{64+4+16} \\[4pt] &=\sqrt{21} \end{align*}\]
Kisha, equation ya nyanja ni\((x+1)^2+(y−3)^2+(z−1)^2=21.\)
Pata usawa wa nyanja na kipenyo\(\overline{PQ}\), wapi\(P=(2,−1,−3)\) na\(Q=(−2,5,−1).\)
- Kidokezo
-
Pata midpoint ya kipenyo kwanza.
- Jibu
-
\[x^2+(y−2)^2+(z+2)^2=14 \nonumber \]
Eleza seti ya pointi ambazo zinatimiza\((x−4)(z−2)=0,\) na kuweka graph.
Suluhisho
Lazima tuwe na\(x−4=0\) ama\(z−2=0\), hivyo seti ya pointi huunda ndege mbili\(x=4\) na\(z=2\) (Kielelezo\(\PageIndex{15}\)).
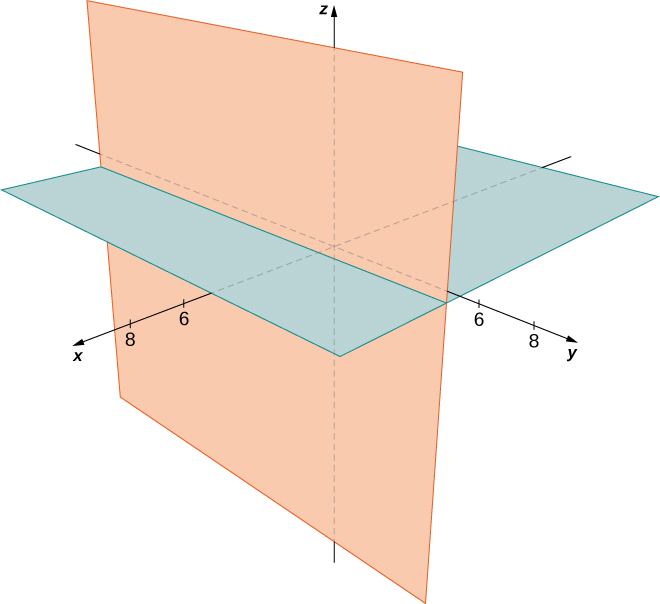
Eleza seti ya pointi ambazo zinatimiza\((y+2)(z−3)=0,\) na kuweka graph.
- Kidokezo
-
Moja ya mambo lazima iwe sifuri.
- Jibu
-
Seti ya pointi huunda ndege mbili\(y=−2\) na\(z=3\).
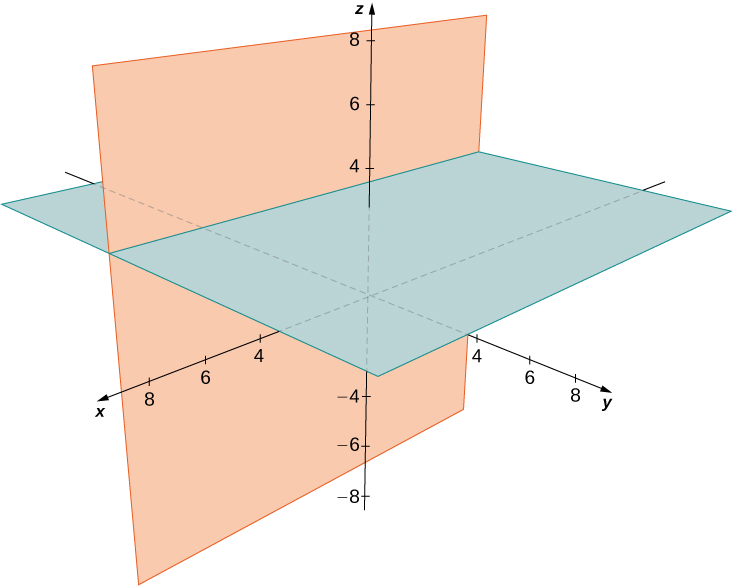
Eleza seti ya pointi katika nafasi tatu-dimensional ambayo inatimiza\((x−2)^2+(y−1)^2=4,\) na grafu kuweka.
Suluhisho
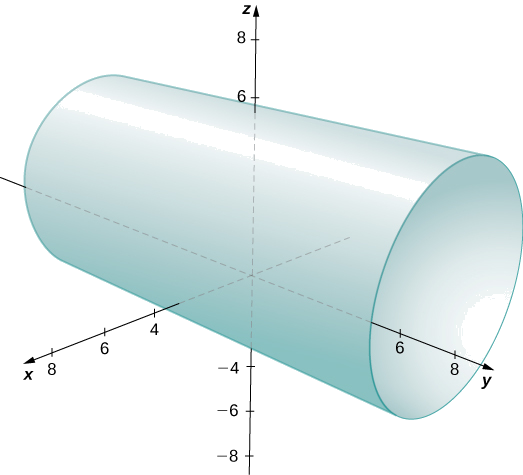
Kuratibu\(x\) - na \(y\)-kuratibu huunda mduara katika \(xy\)-ndege ya radius\(2\), unaozingatia\((2,1)\). Kwa kuwa hakuna kizuizi juu ya \(z\)-kuratibu, matokeo ya tatu-dimensional ni silinda ya mviringo ya radius\(2\) unaozingatia mstari na\(x=2\) na\(y=1\). Silinda inaendelea kwa muda usiojulikana katika\(z\) -mwelekeo (Kielelezo\(\PageIndex{16}\)).
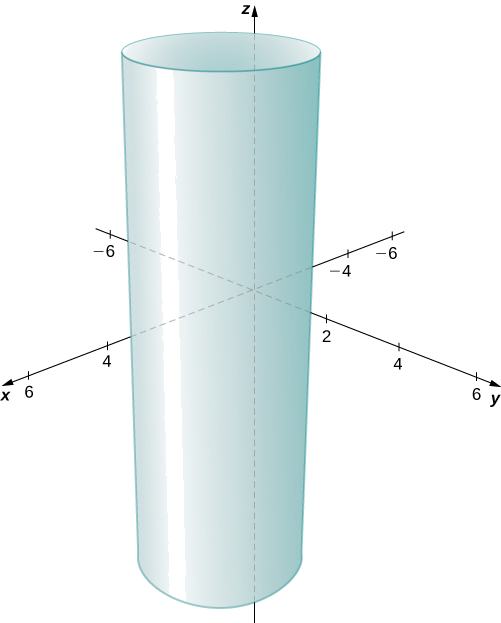
Eleza seti ya pointi katika nafasi tatu dimensional kwamba satisfies\(x^2+(z−2)^2=16\), na grafu uso.
- Kidokezo
-
Fikiria juu ya kile kinachotokea ikiwa unapanga mpango huu kwa vipimo viwili katika\(xz\) -ndege.
- Jibu
-
Silinda ya radius 4 unaozingatia mstari\(x=0\) na\(z=2\).
Kufanya kazi na Vectors katika\(ℝ^3\)
Kama vile vectors mbili-dimensional, vectors tatu-dimensional ni wingi na ukubwa na mwelekeo, na wao ni kuwakilishwa na makundi ya mstari iliyoongozwa (mishale). Kwa vector tatu-dimensional, tunatumia mshale tatu-
Vectors tatu-dimensional pia inaweza kuwakilishwa katika fomu ya sehemu. Uthibitisho\(\vecs{v}=⟨x,y,z⟩\) ni ugani wa asili wa kesi mbili-dimensional, inayowakilisha vector na hatua ya awali katika asili,\((0,0,0)\), na hatua ya mwisho\((x,y,z)\). Vector sifuri ni\(\vecs{0}=⟨0,0,0⟩\). Kwa hiyo, kwa mfano, vector tatu dimensional\(\vecs{v}=⟨2,4,1⟩\) inawakilishwa na sehemu ya mstari iliyoongozwa kutoka hatua\((0,0,0)\) hadi hatua\((2,4,1)\) (Kielelezo\(\PageIndex{17}\)).
Vector kuongeza na kuzidisha scalar hufafanuliwa sawa na kesi mbili-dimensional. Kama\(\vecs{v}=⟨x_1,y_1,z_1⟩\) na\(\vecs{w}=⟨x_2,y_2,z_2⟩\) ni wadudu, na\(k\) ni scalar, basi
\[\vecs{v}+\vecs{w}=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
na
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩. \nonumber \]
Kama\(k=−1,\) basi\(k\vecs{v}=(−1)\vecs{v}\) imeandikwa kama\(−\vecs{v}\), na vector kuondoa hufafanuliwa na\(\vecs{v}−\vecs{w}=\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}\).
Vectors ya kitengo cha kawaida hupanua kwa urahisi katika vipimo vitatu pia\(\hat{\mathbf i}=⟨1,0,0⟩\),\(\hat{\mathbf j}=⟨0,1,0⟩\),, na\(\hat{\mathbf k}=⟨0,0,1⟩\), na tunazitumia kwa njia ile ile tulitumia vectors ya kawaida ya kitengo katika vipimo viwili. Hivyo, tunaweza kuwakilisha vector\(ℝ^3\) kwa njia zifuatazo:
\[\vecs{v}=⟨x,y,z⟩=x\hat{\mathbf i}+y\hat{\mathbf j}+z\hat{\mathbf k} \nonumber \].
Hebu\(\vecd{PQ}\) kuwa vector na hatua ya awali\(P=(3,12,6)\) na uhakika terminal\(Q=(−4,−3,2)\) kama inavyoonekana katika Kielelezo\(\PageIndex{18}\). Eleza\(\vecd{PQ}\) katika fomu zote mbili za sehemu na kutumia vectors ya kawaida ya kitengo.
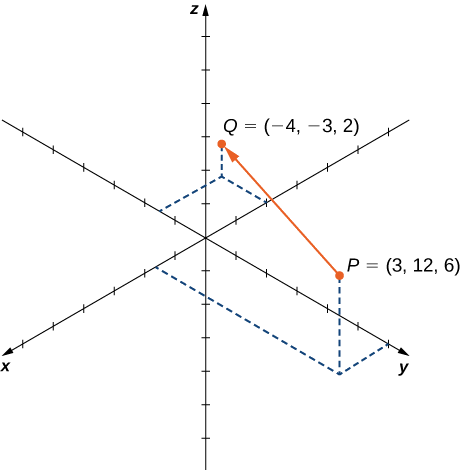
Suluhisho
Katika fomu ya sehemu,
\[\begin{align*} \vecd{PQ} =⟨x_2−x_1,y_2−y_1,z_2−z_1⟩ \\[4pt] =⟨−4−3,−3−12,2−6⟩ \\[4pt] =⟨−7,−15,−4⟩. \end{align*}\]
Katika fomu ya kitengo cha kawaida,
\[\vecd{PQ}=−7\hat{\mathbf i}−15\hat{\mathbf j}−4\hat{\mathbf k}. \nonumber \]
Hebu\(S=(3,8,2)\) na\(T=(2,−1,3)\). Eleza\(\vec{ST}\) katika fomu ya sehemu na katika fomu ya kitengo cha kawaida.
- Kidokezo
-
Andika\(\vecd{ST}\) katika fomu ya sehemu kwanza. \(T\)ni hatua terminal ya\(\vecd{ST}\).
- Jibu
-
\(\vecd{ST}=⟨−1,−9,1⟩=−\hat{\mathbf i}−9\hat{\mathbf j}+\hat{\mathbf k}\)
Kama ilivyoelezwa hapo awali, vectors katika vipimo vitatu hufanya kwa njia sawa na vectors katika ndege. Tafsiri ya kijiometri ya kuongeza vector, kwa mfano, ni sawa katika nafasi mbili na tatu-dimensional (Kielelezo\(\PageIndex{19}\)).
Tumeona jinsi baadhi ya mali ya algebraic ya wadudu, kama vile kuongeza vector na kuzidisha scalar, inaweza kupanuliwa kwa vipimo vitatu. Mali nyingine zinaweza kupanuliwa kwa mtindo sawa. Wao ni muhtasari hapa kwa ajili ya kumbukumbu yetu.
Hebu\(\vecs{v}=⟨x_1,y_1,z_1⟩\) na\(\vecs{w}=⟨x_2,y_2,z_2⟩\) uwe wadudu, na\(k\) uwe na scalar.
- Kuzidisha Scalar:\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
- Vector kuongeza:\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
- Vector kuondoa:\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
- Ukubwa wa vector:\[\|\vecs{v}\|=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
- Kitengo cha vector katika mwelekeo wa\(\vecs{v}\):\[\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\|\vecs{v}\|}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{\|\vecs{v}\|},\dfrac{y_1}{\|\vecs{v}\|},\dfrac{z_1}{\|\vecs{v}\|}⟩, \quad \text{if} \, \vecs{v}≠\vecs{0} \nonumber \]
Tumeona kwamba kuongeza vector katika vipimo viwili satisfies commutative, associative, na livsmedelstillsats inverse mali. Mali hizi za shughuli za vector halali kwa vectors tatu-dimensional pia. Uzidishaji wa vectors wa vectors hutimiza mali ya usambazaji, na vector sifuri hufanya kama utambulisho wa kuongezea. Ushahidi wa kuthibitisha mali hizi kwa vipimo vitatu ni upanuzi wa moja kwa moja wa ushahidi katika vipimo viwili.
Hebu\(\vecs{v}=⟨−2,9,5⟩\) na\(\vecs{w}=⟨1,−1,0⟩\) (Kielelezo\(\PageIndex{20}\)). Pata vectors zifuatazo.
- \(3\vecs{v}−2\vecs{w}\)
- \(5\|\vecs{w}\|\)
- \(\|5 \vecs{w}\|\)
- vector kitengo katika mwelekeo wa\(\vecs{v}\)
Suluhisho
a Kwanza, tumia kuzidisha scalar ya kila vector, kisha uondoe:
\[\begin{align*} 3\vecs{v}−2\vecs{w} =3⟨−2,9,5⟩−2⟨1,−1,0⟩ \\[4pt] =⟨−6,27,15⟩−⟨2,−2,0⟩ \\[4pt] =⟨−6−2,27−(−2),15−0⟩ \\[4pt] =⟨−8,29,15⟩. \end{align*}\]
b Andika equation kwa ukubwa wa vector, kisha kutumia kuzidisha scalar:
\[5\|\vecs{w}\|=5\sqrt{1^2+(−1)^2+0^2}=5\sqrt{2}. \nonumber \]
c Kwanza, tumia kuzidisha kwa scalar, kisha upate ukubwa wa vector mpya. Kumbuka kuwa matokeo ni sawa na kwa sehemu b.:
\[\|5 \vecs{w}\|=∥⟨5,−5,0⟩∥=\sqrt{5^2+(−5)^2+0^2}=\sqrt{50}=5\sqrt{2} \nonumber \]
Kumbuka kwamba kupata vector kitengo katika vipimo viwili, tunagawanya vector kwa ukubwa wake. Utaratibu huo ni sawa katika vipimo vitatu:
\[\begin{align*} \dfrac{\vecs{v}}{\|\vecs{v}\|} =\dfrac{1}{\|\vecs{v}\|}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{(−2)^2+9^2+5^2}}⟨−2,9,5⟩ \\[4pt] =\dfrac{1}{\sqrt{110}}⟨−2,9,5⟩ \\[4pt] =⟨\dfrac{−2}{\sqrt{110}},\dfrac{9}{\sqrt{110}},\dfrac{5}{\sqrt{110}}⟩ . \end{align*}\]
Hebu\(\vecs{v}=⟨−1,−1,1⟩\) na\(\vecs{w}=⟨2,0,1⟩\). Kupata vector kitengo katika mwelekeo wa\(5\vecs{v}+3\vecs{w}.\)
- Kidokezo
-
Anza kwa kuandika\(5\vecs{v}+3\vecs{w}\) katika fomu ya sehemu.
- Jibu
-
\(⟨\dfrac{1}{3\sqrt{10}},−\dfrac{5}{3\sqrt{10}},\dfrac{8}{3\sqrt{10}}⟩\)
Quarterback amesimama kwenye uwanja wa mpira wa miguu akiandaa kutupa kupita. Mpokeaji wake amesimama 20 yd chini ya shamba na 15 yd kushoto quarterback ya. quarterback throws mpira kwa kasi ya 60 mph kuelekea mpokeaji katika angle zaidi ya\(30°\) (kuona takwimu zifuatazo). Andika vector ya awali ya kasi ya mpira,\(\vecs{v}\), katika fomu ya sehemu.
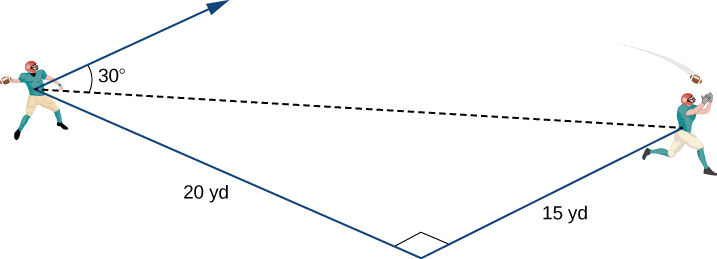
Suluhisho
Jambo la kwanza tunataka kufanya ni kupata vector katika mwelekeo sawa na vector kasi ya mpira. Sisi kisha kuongeza vector ipasavyo ili iwe na ukubwa sahihi. Fikiria vector\(\vecs{w}\) kupanua kutoka mkono quarterback ya uhakika moja kwa moja juu ya kichwa mpokeaji katika pembe ya\(30°\) (kuona takwimu zifuatazo). Vector hii ingekuwa na mwelekeo sawa na\(\vecs{v}\), lakini inaweza kuwa na ukubwa sahihi.
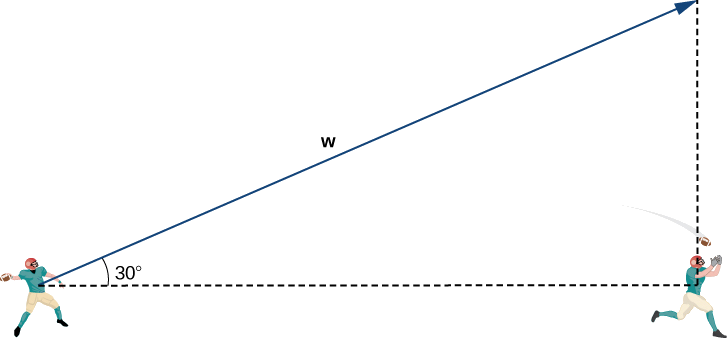
mpokeaji ni 20 yd chini ya shamba na 15 yd kushoto quarterback ya. Kwa hiyo, umbali wa mstari wa moja kwa moja kutoka kwa quarterback hadi mpokeaji ni
Dist kutoka QB kwa mpokeaji\(=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25\) yd.
Sisi tuna,\(\dfrac{25}{\|\vecs{w}\|}=\cos 30°.\) Kisha ukubwa wake\(\vecs{w}\) umetolewa na
\(\|\vecs{w}\|=\dfrac{25}{\cos 30°}=\dfrac{25⋅2}{\sqrt{3}}=\dfrac{50}{\sqrt{3}}\)yd
na umbali wima kutoka receiver kwa uhakika terminal ya\(\vecs{w}\) ni
Vert dist kutoka mpokeaji kwa terminal hatua ya\(\vecs{w}=\|\vecs{w}\| \sin 30°=\dfrac{50}{\sqrt{3}}⋅\dfrac{1}{2}=\dfrac{25}{\sqrt{3}}\) yd.
Kisha\(\vecs{w}=⟨20,15,\dfrac{25}{\sqrt{3}}⟩\), na ina mwelekeo sawa na\(\vecs{v}\).
Kumbuka, ingawa, kwamba sisi mahesabu ukubwa wa\(\vecs{w}\) kuwa\(\|\vecs{w}\|=\dfrac{50}{\sqrt{3}}\) yd, na\(\vecs{v}\) ina ukubwa\(60\) mph. Kwa hiyo, tunahitaji kuzidisha vector\(\vecs{w}\) kwa mara kwa mara sahihi,\(k\). Tunataka kupata thamani ya\(k\) ili\(∥k\vecs{w}∥=60\) mph *. Tuna
\(\|k \vecs{w}\|=k\|\vecs{w}\|=k\dfrac{50}{\sqrt{3}}\)yd,
hivyo tunataka
\(k \left(\dfrac{50}{\sqrt{3}}\text{ yd}\right) =60\)mph
\(k=\dfrac{60\sqrt{3}}{50}\)mph/yd
\(k=\dfrac{6\sqrt{3}}{5}\)mph/yd.
Kisha
\(\vecs{v}=k\vecs{w}=k⟨20,15,\dfrac{25}{\sqrt{3}}⟩=\dfrac{6\sqrt{3}}{5}\;⟨20,15,\dfrac{25}{\sqrt{3}}⟩=⟨24\sqrt{3},18\sqrt{3},30⟩\).
Hebu mara mbili kuangalia kwamba\(\|\vecs{v}\|=60\) mph. Tuna
\(\|\vecs{v}\|=\sqrt{(24\sqrt{3})^2+(18\sqrt{3})^2+(30)^2}=\sqrt{1728+972+900}=\sqrt{3600}=60\)mph.
Kwa hiyo, tumepata vipengele sahihi kwa\(\vecs{v}\).
Wasomaji ambao wamekuwa wakiangalia vitengo vya kipimo wanaweza kuwa wanashangaa nini hasa kinachoendelea katika hatua hii: je! Sisi sio tu mchanganyiko wa yadi na maili kwa saa? Hatuna, lakini sababu ni ya hila. Njia moja ya kuelewa ni kutambua kwamba kuna mifumo miwili ya kuratibu sambamba katika tatizo hili: moja inatoa nafasi chini ya shamba, kote shamba, na hadi hewa katika vitengo vya yadi; nyingine inatoa kasi chini ya shamba, kote shamba, na hadi hewa katika vitengo vya maili kwa saa. Vector\(\vecs{w}\) ni mahesabu katika nafasi ya kuratibu mfumo; vector\(\vecs{v}\) itakuwa katika mfumo wa kasi. Kwa sababu axes sambamba katika kila mfumo ni sambamba, maelekezo katika mifumo miwili pia ni sawa, hivyo madai kwamba\(\vecs{w}\) na\(\vecs{v}\) uhakika katika mwelekeo huo ni sahihi. Mara kwa mara\(k\) kwamba sisi ni kuangalia kwa ni sababu ya uongofu kati ya ukubwa wa wadudu hawa wawili, kubadilisha kutoka mfumo nafasi kwa kasi moja katika mchakato. Na kama inavyoonekana hapo juu, hesabu yetu ya\(k\) inazalisha vitengo sahihi kwa uongofu huo, yaani maili kwa saa kwa yadi.
Kudhani quarterback na mpokeaji ni katika sehemu moja kama katika mfano uliopita. Wakati huu, hata hivyo, quarterback throws mpira kwa kasi ya\(40\) mph na angle ya\(45°\). Andika vector ya awali ya kasi ya mpira,\(\vecs{v}\), katika fomu ya sehemu.
- Kidokezo
-
Fuata mchakato uliotumiwa katika mfano uliopita.
- Jibu
-
\(v=⟨16\sqrt{2},12\sqrt{2},20\sqrt{2}⟩\)
Dhana muhimu
- Mfumo wa kuratibu tatu-dimensional umejengwa karibu na seti ya shaba tatu ambazo zinaingiliana kwenye pembe za kulia kwa hatua moja, asili. Triples\((x,y,z)\) zilizoamriwa hutumiwa kuelezea eneo la uhakika katika nafasi.
- Umbali\(d\) kati ya pointi\((x_1,y_1,z_1)\) na\((x_2,y_2,z_2)\) hutolewa na formula\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2}.\nonumber \]
- Katika vipimo vitatu, equations\(x=a,\, y=b,\) na\(z=c\) kuelezea ndege ambazo ni sambamba na kuratibu ndege.
- Equation ya kiwango cha nyanja na kituo\((a,b,c)\) na radius\(r\) ni\[(x−a)^2+(y−b)^2+(z−c)^2=r^2. \nonumber \]
- Katika vipimo vitatu, kama ilivyo katika mbili, vectors huelezwa kwa fomu ya sehemu\(\vecs v=⟨x,y,z⟩\), au kwa mujibu wa vectors ya kawaida ya kitengo,\(\vecs v= x\,\mathbf{\hat i}+y\,\mathbf{\hat j}+z\,\mathbf{\hat k}.\)
- Mali ya vectors katika nafasi ni ugani wa asili wa mali kwa vectors katika ndege. Hebu\(\vecs v=⟨x_1,y_1,z_1⟩\) na\(\vecs w=⟨x_2,y_2,z_2⟩\) uwe wadudu, na\(k\) uwe na scalar.
Kuzidisha Scalar:
\[k\vecs{v}=⟨kx_1,ky_1,kz_1⟩ \nonumber \]
Vector kuongeza:
\[\vecs{v}+\vecs{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩ \nonumber \]
Vector kuondoa:
\[\vecs{v}−\vecs{w}=⟨x_1,y_1,z_1⟩−⟨x_2,y_2,z_2⟩=⟨x_1−x_2,y_1−y_2,z_1−z_2⟩ \nonumber \]
Vector ukubwa:
\[‖\vecs{v}‖=\sqrt{x_1^2+y_1^2+z_1^2} \nonumber \]
Kitengo cha vector katika mwelekeo wa\(\vecs{v}\):
\[\dfrac{\vecs{v}}{‖\vecs{v}‖}=\dfrac{1}{‖\vecs{v}‖}⟨x_1,y_1,z_1⟩=⟨\dfrac{x_1}{‖\vecs{v}‖},\dfrac{y_1}{‖\vecs{v}‖},\dfrac{z_1}{‖\vecs{v}‖}⟩, \; \vecs{v}≠\vecs{0} \nonumber \]
Mlinganyo muhimu
Umbali kati ya pointi mbili katika nafasi:
\[d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2+(z_2−z_1)^2} \nonumber \]
Sphere na kituo\((a,b,c)\) na radius\(r\):
\[(x−a)^2+(y−b)^2+(z−c)^2=r^2 \nonumber \]
faharasa
- kuratibu ndege
- ndege iliyo na safu mbili za kuratibu tatu katika mfumo wa kuratibu tatu-dimensional, jina lake na axes ina:\(xy\) -plane,\(xz\) -plane, au\(yz\) -plane
- utawala wa mkono wa kulia
- njia ya kawaida ya kufafanua mwelekeo wa mfumo wa kuratibu tatu-dimensional; wakati mkono wa kulia unapigwa karibu na\(z\) mhimili kwa njia ambayo vidole vinapunguza kutoka kwa\(x\) mhimili mzuri hadi kwenye\(y\) mhimili mzuri, pointi za kidole katika mwelekeo wa\(z\) mhimili mzuri
- octants
- mikoa nane ya nafasi iliyoundwa na ndege kuratibu
- nyanja
- seti ya pointi zote equidistant kutoka hatua fulani inayojulikana kama kituo cha
- equation ya kawaida ya nyanja
- \((x−a)^2+(y−b)^2+(z−c)^2=r^2\)inaelezea nyanja na kituo\((a,b,c)\) na radius\(r\)
- mfumo wa kuratibu mstatili wa tatu
- mfumo wa kuratibu unaofafanuliwa na mistari mitatu inayoingiliana kwenye pembe za kulia; kila hatua katika nafasi inaelezewa na mara tatu iliyoagizwa\((x,y,z)\) ambayo inahusisha eneo lake kuhusiana na axes zinazofafanua
Wachangiaji
Mfano\(\PageIndex{10}\) umebadilishwa na Doug Baldwin na Paul Seeburger kufafanua vitengo vya kipimo ambavyo hutumia na jinsi inavyotumia.
Paul Seeburger pia aliunda matoleo ya nguvu ya Takwimu\(\PageIndex{8}, \PageIndex{9}\) na\(\PageIndex{13}\) kutumia CalcPlot3D.


