11.5: Sehemu za Conic
- Page ID
- 178428
- Tambua equation ya parabola katika fomu ya kawaida na lengo lililopewa na directrix.
- Tambua equation ya ellipse katika fomu ya kawaida na foci iliyotolewa.
- Tambua equation ya hyperbola katika fomu ya kawaida na foci iliyotolewa.
- Tambua parabola, ellipse, au hyperbola kutoka thamani yake ya eccentricity.
- Andika equation ya polar ya sehemu ya conic na eccentricity\(e\).
- Tambua wakati equation ya jumla ya shahada mbili ni parabola, duaradufu, au hyperbola.
Sehemu za Conic zimejifunza tangu wakati wa Wagiriki wa kale, na zilionekana kuwa dhana muhimu ya hisabati. Mapema 320 BCE, wanahisabati wa Kigiriki kama Menaechmus, Appollonius, na Archimedes walivutiwa na curves hizi. Appollonius aliandika makala nzima ya nane juu ya sehemu za conic ambazo alikuwa, kwa mfano, na uwezo wa kupata njia maalum ya kutambua sehemu ya conic kupitia matumizi ya jiometri. Tangu wakati huo, matumizi muhimu ya sehemu za conic yametokea (kwa mfano, katika astronomy), na mali ya sehemu za conic hutumiwa katika darubini za redio, kupokea sahani za satellite, na hata usanifu. Katika sehemu hii tunazungumzia sehemu tatu za msingi za conic, baadhi ya mali zao, na usawa wao.
Sehemu za conic hupata jina lao kwa sababu zinaweza kuzalishwa kwa kuingiliana ndege na koni. Koni ina sehemu mbili za umbo la kufanana zinazoitwa nappes. Nappe moja ni nini watu wengi wanamaanisha kwa “koni,” kuwa na sura ya kofia ya chama. Koni ya mviringo ya kulia inaweza kuzalishwa kwa kugeuka mstari unaopita kupitia asili karibu na y -axis kama inavyoonekana kwenye Kielelezo\(\PageIndex{1}\).
Sehemu za conic zinazalishwa na makutano ya ndege yenye koni (Kielelezo\(\PageIndex{2}\)). Ikiwa ndege ni sawa na mhimili wa mapinduzi (y -axis), basi sehemu ya conic ni hyperbola. Ikiwa ndege ni sawa na mstari wa kuzalisha, sehemu ya conic ni parabola. Ikiwa ndege ni perpendicular kwa mhimili wa mapinduzi, sehemu ya conic ni mduara. Ikiwa ndege inakabiliana na nappe moja kwa pembe kwa mhimili (zaidi ya
Parabola
Parabola huzalishwa wakati ndege inakabiliana na koni inayofanana na mstari wa kuzalisha. Katika kesi hiyo, ndege inakabiliana na moja tu ya nappes. Parabola pia inaweza kuelezwa kwa suala la umbali.
Parabola ni seti ya pointi zote ambazo umbali kutoka kwenye hatua ya kudumu, inayoitwa lengo, ni sawa na umbali kutoka kwenye mstari uliowekwa, unaoitwa directrix. Nusu ya nusu kati ya lengo na directrix inaitwa vertex ya parabola.
Grafu ya parabola ya kawaida inaonekana kwenye Kielelezo\(\PageIndex{3}\). Kutumia mchoro huu kwa kushirikiana na formula ya umbali, tunaweza kupata equation kwa parabola. Kumbuka formula ya umbali: Kutokana na hatua P\((x_1,y_1)\) na kuratibu na uhakika Q na kuratibu\((x_2,y_2),\) umbali kati yao hutolewa na formula
\[d(P,Q)=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Kisha kutokana na ufafanuzi wa parabola na Kielelezo\(\PageIndex{3}\), tunapata
\[d(F,P)=d(P,Q) \nonumber \]
\[\sqrt{(0−x)^2+(p−y)^2}=\sqrt{(x−x)^2+(−p−y)^2}. \nonumber \]
Kupiga pande zote mbili na kurahisisha mavuno
\[ \begin{align} x^2+(p−y)^2 = 0^2+(−p−y)^2 \\ x^2+p^2−2py+y^2 = p^2+2py+y^2 \\ x^2−2py =2py \\ x^2 =4py. \end{align} \nonumber \]
Sasa tuseme tunataka kuhamisha vertex. Tunatumia vigezo\((h,k)\) ili kutaja kuratibu za vertex. Kisha kama lengo ni moja kwa moja juu ya vertex, ina kuratibu\((h,k+p)\) na directrix ina equation\(y=k−p\). Kupitia derivation sawa huzaa formula\((x−h)^2=4p(y−k)\). Kutatua equation hii kwa\(y\) inaongoza kwa theorem zifuatazo.
Kutokana parabola kufungua juu na vertex iko katika\((h,k)\) na lengo iko katika\((h,k+p)\), ambapo\(p\) ni mara kwa mara, equation kwa parabola ni kutolewa na
\[y=\dfrac{1}{4p}(x−h)^2+k. \nonumber \]
Hii ni fomu ya kawaida ya parabola.
Tunaweza pia kujifunza kesi wakati parabola inafungua au kushoto au kulia. Equation kwa kila moja ya kesi hizi pia inaweza kuandikwa kwa fomu ya kawaida kama inavyoonekana katika grafu zifuatazo.
Kwa kuongeza, equation ya parabola inaweza kuandikwa kwa fomu ya jumla, ingawa kwa fomu hii maadili ya\(h\),\(k\), na\(p\) hayatambui mara moja. Aina ya jumla ya parabola imeandikwa kama
\[ax^2+bx+cy+d=0 \label{para1} \]
au
\[ay^2+bx+cy+d=0.\label{para2} \]
Equation\ ref {para1} inawakilisha parabola inayofungua ama juu au chini. Equation\ ref {para2} inawakilisha parabola inayofungua ama kushoto au kulia. Ili kuweka equation katika fomu ya kawaida, tumia njia ya kukamilisha mraba.
Weka equation
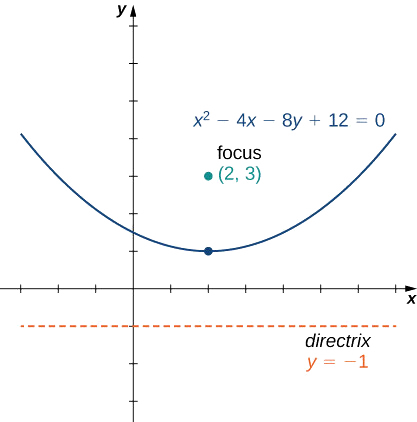
\[x^2−4x−8y+12=0 \nonumber \]
katika hali ya kawaida na grafu parabola kusababisha.
Suluhisho
Kwa kuwa y si squared katika equation hii, tunajua kwamba parabola kufungua ama juu au chini. Kwa hiyo tunahitaji kutatua equation hii kwa y, ambayo kuweka equation katika fomu ya kawaida. Ili kufanya hivyo, kwanza ongeza\(8y\) pande zote mbili za equation:
\[8y=x^2−4x+12. \nonumber \]
Hatua inayofuata ni kukamilisha mraba upande wa kulia. Anza kwa kuunganisha maneno mawili ya kwanza upande wa kulia kwa kutumia mabano:
\[8y=(x^2−4x)+12. \nonumber \]
Next kuamua mara kwa mara kwamba, wakati aliongeza ndani ya mabano, hufanya wingi ndani ya mabano kamili mraba trinomial. Ili kufanya hivyo, chukua nusu ya mgawo wa x na mraba. Hii inakupa\((\dfrac{−4}{2})^2=4.\) Kuongeza 4 ndani ya mabano na Ondoa 4 nje ya mabano, hivyo thamani ya equation haijabadilishwa:
\[8y=(x^2−4x+4)+12−4. \nonumber \]
Sasa kuchanganya kama maneno na kuzingatia wingi ndani ya mabano:
\[8y=(x−2)^2+8. \nonumber \]
Hatimaye, ugawanye na 8:
\[y=\dfrac{1}{8}(x−2)^2+1. \nonumber \]
Equation hii ni sasa katika hali ya kawaida. Kulinganisha hii kwa Equation anatoa\(h=2, k=1\), na\(p=2\). Parabola inafungua, na vertex katika\((2,1)\), kuzingatia\((2,3)\), na directrix\(y=−1\). Grafu ya parabola hii inaonekana kama ifuatavyo.
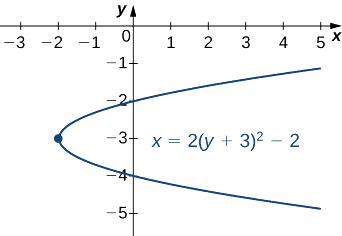
Weka equation\(2y^2−x+12y+16=0\) katika fomu ya kawaida na graph parabola kusababisha.
- Kidokezo
-
Kutatua kwa\(x\). Angalia mwelekeo gani parabola inafungua.
- Jibu
-
\[x=2(y+3)^2−2 \nonumber \]
Mhimili wa ulinganifu wa parabola ya wima (kufungua au chini) ni mstari wa wima unaopitia kipeo. Parabola ina mali ya kutafakari ya kuvutia. Tuseme tuna sahani ya satellite na sehemu ya msalaba wa parabolic. Ikiwa boriti ya mawimbi ya sumakuumeme, kama vile mawimbi ya mwanga au redio, inakuja kwenye sahani kwenye mstari wa moja kwa moja kutoka kwa satelaiti (sambamba na mhimili wa ulinganifu), basi mawimbi yanaonyesha sahani na kukusanya kwenye lengo la parabola kama inavyoonekana.
Fikiria sahani ya parabolic iliyoundwa kukusanya ishara kutoka kwa satellite katika nafasi. Safu hiyo inalenga moja kwa moja kwenye satellite, na mpokeaji iko kwenye lengo la parabola. Mawimbi ya redio yanayotokana na satellite yanajitokeza kwenye uso wa parabola kwa mpokeaji, ambayo hukusanya na huamua ishara za digital. Hii inaruhusu mpokeaji mdogo kukusanya ishara kutoka angle pana ya angani. Vipande vya taa na vichwa vya gari hufanya kazi kwa kanuni sawa, lakini kinyume chake: chanzo cha mwanga (yaani, bomba la taa) iko kwenye lengo na uso unaoonyesha kwenye kioo cha parabolic inalenga boriti moja kwa moja mbele. Hii inaruhusu bulb ndogo ya mwanga kuangaza angle pana ya nafasi mbele ya tochi au gari.
duaradufu
Ellipse pia inaweza kuelezwa kwa suala la umbali. Katika kesi ya ellipse, kuna foci mbili (wingi wa lengo), na maelekezo mawili (wingi wa directrix). Tunaangalia maelekezo kwa undani zaidi baadaye katika sehemu hii.
ellipse ni seti ya pointi zote ambazo jumla ya umbali wao kutoka pointi mbili fasta (foci) ni mara kwa mara.
Grafu ya ellipse ya kawaida inavyoonyeshwa kwenye Mchoro\(\PageIndex{6}\). Katika takwimu hii foci ni lebo kama\(F\) na\(F′\). Wote wawili ni umbali sawa kutoka kwa asili, na umbali huu unawakilishwa na kutofautiana\(c\). Kwa hiyo kuratibu za\(F\) ni\((c,0)\) na kuratibu za\(F′\) ni\((−c,0).\) pointi\(P\) na\(P′\) ziko katika mwisho wa mhimili mkubwa wa duaradufu, na kuwa na kuratibu\((a,0)\) na\((−a,0)\), kwa mtiririko huo. Mhimili mkubwa daima ni umbali mrefu zaidi katika duaradufu, na inaweza kuwa usawa au wima. Hivyo, urefu wa mhimili mkubwa katika duaradufu hii ni\(2a\). Zaidi ya hayo,\(P\) na\(P′\) huitwa vertices ya duaradufu. Pointi\(Q\) na\(Q′\) ziko katika mwisho wa mhimili mdogo wa duaradufu, na kuwa na kuratibu\((0,b)\) na\((0,−b),\) kwa mtiririko huo. Mhimili mdogo ni umbali mfupi zaidi katika duaradufu. Mhimili mdogo ni perpendicular kwa mhimili mkubwa.
Kwa mujibu wa ufafanuzi wa ellipse, tunaweza kuchagua hatua yoyote juu ya ellipse na jumla ya umbali kutoka hatua hii hadi foci mbili ni mara kwa mara. Tuseme sisi kuchagua uhakika\(P\). Tangu kuratibu ya uhakika\(P\) ni\((a,0),\) jumla ya umbali ni
\[d(P,F)+d(P,F′)=(a−c)+(a+c)=2a. \nonumber \]
Kwa hiyo jumla ya umbali kutoka hatua ya kiholela A na kuratibu pia\((x,y)\) ni sawa na\(2a\). Kutumia formula ya umbali, tunapata
\[d(A,F)+d(A,F′)=2a. \nonumber \]
\[\sqrt{(x−c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \nonumber \]
Ondoa radical ya pili kutoka pande zote mbili na mraba pande zote mbili:
\[\sqrt{(x−c)^2+y^2}=2a−\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Sasa jitenga radical upande wa kulia na mraba tena:
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx \nonumber \]
\[4a\sqrt{(x+c)^2+y^2}=4a^2+4cx \nonumber \]
\[\sqrt{(x+c)^2+y^2}=a+\dfrac{cx}{a} \nonumber \]
\[(x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}. \nonumber \]
Sulua vigezo upande wa kushoto wa equation na constants upande wa kulia:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Gawanya pande zote mbili na\(a^2−c^2\). Hii inatoa equation
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Ikiwa tunarudi kwenye Kielelezo\(\PageIndex{6}\), basi urefu wa kila moja ya makundi mawili ya mstari wa kijani ni sawa na\(a\). Hii ni kweli kwa sababu jumla ya umbali kutoka hatua\(Q\) hadi foci\(F\) na\(F′\) ni sawa na\(2a\), na urefu wa makundi haya mawili ya mstari ni sawa. Sehemu hii ya mstari huunda pembetatu sahihi na urefu wa hypotenuse\(a\) na urefu wa mguu\(b\) na\(c\). Kutoka theorem ya Pythagorean,\(b^2+c^2=a^2\) na\(b^2=a^2−c^2\). Kwa hiyo equation ya duaradufu inakuwa
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \nonumber \]
Hatimaye, kama katikati ya duaradufu ni wakiongozwa kutoka asili kwa uhakika\((h,k)\), tuna zifuatazo kiwango fomu ya duaradufu.
Fikiria ellipse na katikati\((h,k)\), mhimili mkubwa wa usawa na urefu\(2a\), na mhimili mdogo wa wima na urefu\(2b\). Kisha equation ya duaradufu hii katika fomu ya kawaida ni
\[\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1 \label{HorEllipse} \]
na foci ziko\((h±c,k)\), wapi\(c^2=a^2−b^2\). Ulinganisho wa maelekezo ni\(x=h±\dfrac{a^2}{c}\).
Ikiwa mhimili mkubwa ni wima, basi equation ya ellipse inakuwa
\[\dfrac{(x−h)^2}{b^2}+\dfrac{(y−k)^2}{a^2}=1 \label{VertEllipse} \]
na foci ziko\((h,k±c)\), wapi\(c^2=a^2−b^2\). Ulinganisho wa maelekezo katika kesi hii ni\(y=k±\dfrac{a^2}{c}\).
Ikiwa mhimili mkubwa ni usawa, basi duaradufu inaitwa usawa, na kama mhimili mkubwa ni wima, basi duaradufu inaitwa wima. Ulinganisho wa duaradufu ni kwa fomu ya jumla ikiwa iko katika fomu
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
ambapo A na B ni ama chanya au zote mbili hasi. Ili kubadilisha equation kutoka kwa ujumla hadi fomu ya kawaida, tumia njia ya kukamilisha mraba.
Weka equation
\[9x^2+4y^2−36x+24y+36=0 \nonumber \]
katika fomu ya kawaida na grafu kusababisha duaradufu.
Suluhisho
Kwanza Ondoa 36 kutoka pande zote mbili za equation:
\[9x^2+4y^2−36x+24y=−36. \nonumber \]
Next kundi\(x\) maneno pamoja na\(y\) masharti pamoja, na sababu nje sababu ya kawaida:
\[(9x^2−36x)+(4y^2+24y)=−36 \nonumber \]
\[9(x^2−4x)+4(y^2+6y)=−36. \nonumber \]
Tunahitaji kuamua mara kwa mara kwamba, wakati umeongezwa ndani ya kila seti ya mabano, husababisha mraba kamili. Katika seti ya kwanza ya mabano, chukua nusu ya mgawo wa x na mraba. Hii inatoa\((\dfrac{−4}{2})^2=4.\) Katika seti ya pili ya mabano, chukua nusu ya mgawo wa y na mraba. Hii inakupa\((\dfrac{6}{2})^2=9.\) Kuongeza hizi ndani ya kila jozi ya mabano. Tangu seti ya kwanza ya mabano ina 9 mbele, sisi ni kweli kuongeza 36 kwa upande wa kushoto. Vile vile, tunaongeza 36 kwenye seti ya pili pia. Kwa hiyo equation inakuwa
\[9(x^2−4x+4)+4(y^2+6y+9)=−36+36+36 \nonumber \]
\[9(x^2−4x+4)+4(y^2+6y+9)=36. \nonumber \]
Sasa fanya seti zote mbili za mabano na ugawanye na 36:
\[9(x−2)^2+4(y+3)^2=36 \nonumber \]
\[\dfrac{9(x−2)^2}{36}+\dfrac{4(y+3)^2}{36}=1 \nonumber \]
\[\dfrac{(x−2)^2}{4}+\dfrac{(y+3)^2}{9}=1. \nonumber \]
Equation sasa iko katika fomu ya kawaida. Kulinganisha hii kwa Equation\ ref {Vertellipse} anatoa\(h=2, k=−3, a=3,\) na\(b=2\). Hii ni duaradufu wima na kituo cha saa\((2,−3)\), mhimili kuu 6, na mhimili mdogo 4. Grafu ya ellipse hii inaonekana kama ifuatavyo.

Weka equation
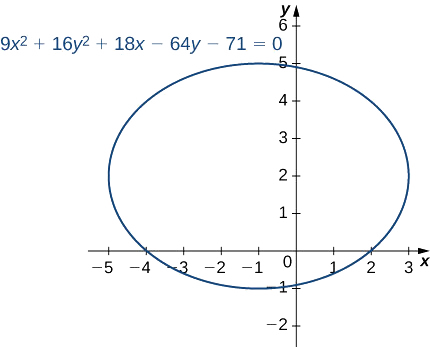
\[9x^2+16y^2+18x−64y−71=0 \nonumber \]
katika fomu ya kawaida na grafu kusababisha duaradufu.
- Kidokezo
-
Hoja mara kwa mara juu na kukamilisha mraba.
- Jibu
-
\[\dfrac{(x+1)^2}{16}+\dfrac{(y−2)^2}{9}=1 \nonumber \]
Kwa mujibu wa sheria ya kwanza ya Kepler ya mwendo wa sayari, obiti ya sayari inayozunguka Jua ni duaradufu na Jua kwenye moja ya foci kama inavyoonekana kwenye Mchoro\(\PageIndex{8A}\). Kwa sababu obiti ya Dunia ni duaradufu, umbali kutoka Jua hutofautiana mwaka mzima. Mawazo yasiyofaa ya kawaida ni kwamba Dunia iko karibu na Jua wakati wa majira ya joto. Kwa kweli, katika majira ya joto kwa hemphere ya kaskazini, Dunia ni mbali zaidi na Jua kuliko wakati wa majira ya baridi. Tofauti katika msimu husababishwa na kutembea kwa mhimili wa Dunia katika ndege ya orbital. Comets zinazozunguka Jua, kama vile Comet ya Halley, pia zina mizunguko ya elliptical, kama vile miezi inayozunguka sayari na satelaiti zinazozunguka Dunia.
Ellipses pia ina mali ya kutafakari ya kuvutia: ray mwanga inayotokana na lengo moja hupita kupitia lengo lingine baada ya kutafakari kioo katika duaradufu. Kitu kimoja kinatokea kwa wimbi la sauti pia. National Statuary Hall katika Capitol Marekani katika Washington, DC, ni chumba maarufu katika sura elliptical kama inavyoonekana katika Kielelezo\(\PageIndex{8B}\). Ukumbi huu uliwahi kuwa mahali pa mkutano kwa Baraza la Wawakilishi wa Marekani kwa karibu miaka hamsini. Eneo la foci mbili za chumba hiki cha nusu ya elliptical ni wazi kutambuliwa na alama kwenye sakafu, na hata kama chumba kinajaa wageni, wakati watu wawili wamesimama kwenye maeneo haya na kuzungumza na kila mmoja, wanaweza kusikia kila mmoja kwa uwazi zaidi kuliko wanaweza kusikia mtu amesimama karibu. Legend ina kuwa John Quincy Adams alikuwa dawati lake iko kwenye moja ya foci na alikuwa na uwezo wa eavesdrop juu ya kila mtu mwingine katika House bila milele wanaohitaji kusimama. Ingawa hii inafanya hadithi nzuri, haiwezekani kuwa kweli, kwa sababu dari ya awali ilizalisha echoes nyingi kwamba chumba nzima kilikuwa na hung na mazulia ili kupunguza kelele. Dari ilijengwa upya mwaka wa 1902 na kisha tu athari inayojulikana sasa ya whispering iliibuka. Nyumba nyingine maarufu ya whispering - tovuti ya mapendekezo mengi ya ndoa-iko katika Grand Central Station huko New York City.
Hyperbolas
Hyperbola pia inaweza kuelezwa kwa umbali. Katika kesi ya hyperbola, kuna maelekezo mawili na mbili. Hyperbolas pia ina asymptotes mbili.
Hyperbola ni seti ya pointi zote ambapo tofauti kati ya umbali wao kutoka pointi mbili fasta (foci) ni mara kwa mara.
Grafu ya hyperbola ya kawaida inaonekana kama ifuatavyo.
Kupatikana kwa equation ya hyperbola katika fomu ya kawaida ni sawa na ile ya ellipse. Hitch moja kidogo iko katika ufafanuzi: Tofauti kati ya namba mbili daima ni chanya. Hebu\(P\) kuwa hatua juu ya hyperbola na kuratibu\((x,y)\). Kisha ufafanuzi wa hyperbola hutoa\(|d(P,F_1)−d(P,F_2)|=constant\). Ili kurahisisha derivation, kudhani kuwa\(P\) iko kwenye tawi la haki la hyperbola, hivyo baa za thamani kabisa zinashuka. Ikiwa iko kwenye tawi la kushoto, basi uondoaji umebadilishwa. Vertex ya tawi la haki ina kuratibu\((a,0),\) hivyo
\[d(P,F_1)−d(P,F_2)=(c+a)−(c−a)=2a. \nonumber \]
equation hii kwa hiyo ni kweli kwa hatua yoyote juu ya hyperbola. Kurudi kwenye kuratibu\((x,y)\) kwa\(P\):
\[d(P,F_1)−d(P,F_2)=2a \nonumber \]
\[\sqrt{(x+c)^2+y^2}−\sqrt{(x−c)^2+y^2}=2a. \nonumber \]
Sulua pili radical na mraba pande zote mbili:
\[\sqrt{(x−c)^2+y^2}=-2a+\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Sasa jitenga radical upande wa kulia na mraba tena:
\(−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx\)
\(-4a\sqrt{(x+c)^2+y^2}=−4a^2−4cx\)
\(-\sqrt{(x+c)^2+y^2}=−a−\dfrac{cx}{a}\)
\((x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}\).
Sulua vigezo upande wa kushoto wa equation na constants upande wa kulia:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Hatimaye, kugawanya pande zote mbili na\(a^2−c^2\). Hii inatoa equation
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Sasa tunafafanua b ili\(b^2=c^2−a^2\). Hii inawezekana kwa sababu\(c>a\). Kwa hiyo, equation ya hyperbola inakuwa
\[\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1. \nonumber \]
Hatimaye, kama kituo cha hyperbola ni wakiongozwa kutoka asili kwa uhakika\((h,k),\) tuna zifuatazo kiwango fomu ya hyperbola.
Fikiria hyperbola na kituo\((h,k)\), mhimili mkubwa wa usawa, na mhimili mdogo wa wima. Kisha equation ya hyperbola hii ni
\[\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1 \label{HorHyperbola} \]
na foci ziko\((h±c,k),\) wapi\(c^2=a^2+b^2\). Equations ya asymptotes hutolewa na\(y=k±\dfrac{b}{a}(x−h).\) equations ya maelekezo ni
\[x=h±\dfrac{a^2}{\sqrt{a^2+b^2}}=h±\dfrac{a^2}{c} \nonumber \]
Ikiwa mhimili mkubwa ni wima, basi equation ya hyperbola inakuwa
\[\dfrac{(y−k)^2}{a^2}−\dfrac{(x−h)^2}{b^2}=1 \nonumber \]
na foci ziko\((h,k±c),\) wapi\(c^2=a^2+b^2\). Ulinganisho wa asymptotes hutolewa na\(y=k±\dfrac{a}{b}(x−h)\). Ulinganisho wa maelekezo ni
\[y=k±\dfrac{a^2}{\sqrt{a^2+b^2}}=k±\dfrac{a^2}{c}. \nonumber \]
Ikiwa mhimili mkubwa (mhimili wa mzunguko) ni usawa, basi hyperbola inaitwa usawa, na kama mhimili mkubwa ni wima basi hyperbola inaitwa wima. Equation ya hyperbola ni kwa fomu ya jumla ikiwa iko katika fomu
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
ambapo A na B wana ishara tofauti. Ili kubadilisha equation kutoka kwa ujumla hadi fomu ya kawaida, tumia njia ya kukamilisha mraba.
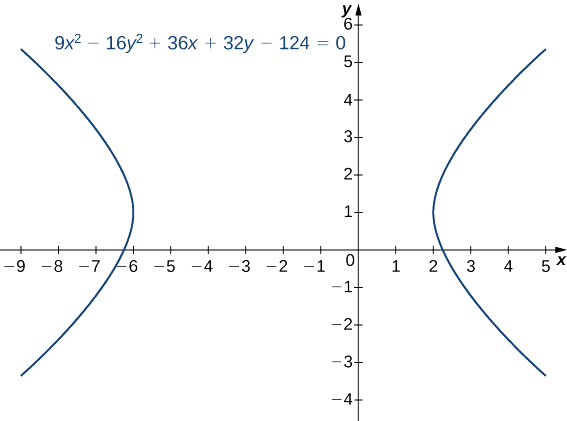
Weka equation\(9x^2−16y^2+36x+32y−124=0\) katika fomu ya kawaida na grafu hyperbola kusababisha. Je, ni equations ya asymptotes?
Suluhisho
Kwanza ongeza 124 kwa pande zote mbili za equation:
\(9x^2−16y^2+36x+32y=124.\)
Kundi linalofuata maneno x pamoja na maneno y pamoja, kisha ueleze mambo ya kawaida:
\((9x^2+36x)−(16y^2−32y)=124\)
\(9(x^2+4x)−16(y^2−2y)=124\).
Tunahitaji kuamua mara kwa mara kwamba, wakati umeongezwa ndani ya kila seti ya mabano, husababisha mraba kamili. Katika seti ya kwanza ya mabano, chukua nusu ya mgawo wa x na mraba. Hii inatoa\((\dfrac{4}{2})^2=4\). Katika seti ya pili ya mabano, chukua nusu ya mgawo wa y na mraba. Hii inakupa\((\dfrac{−2}{2})^2=1.\) Kuongeza hizi ndani ya kila jozi ya mabano. Tangu seti ya kwanza ya mabano ina 9 mbele, sisi ni kweli kuongeza 36 kwa upande wa kushoto. Vile vile, tunaondoa 16 kutoka seti ya pili ya mabano. Kwa hiyo equation inakuwa
\(9(x^2+4x+4)−16(y^2−2y+1)=124+36−16\)
\(9(x^2+4x+4)−16(y^2−2y+1)=144.\)
Sababu inayofuata seti zote mbili za mabano na kugawanya na 144:
\(9(x+2)^2−16(y−1)^2=144\)
\(\dfrac{9(x+2)^2}{144}−\dfrac{16(y−1)^2}{144}=1\)
\(\dfrac{(x+2)^2}{16}−\dfrac{(y−1)^2}{9}=1.\)
Equation sasa iko katika fomu ya kawaida. Kulinganisha hii kwa Equation\ ref {horHyperBola} anatoa\(h=−2, k=1, a=4,\) na\(b=3\). Hii ni hyperbola ya usawa na katikati\((−2,1)\) na asymptotes iliyotolewa na equations\(y=1±\dfrac{3}{4}(x+2)\). Grafu ya hyperbola hii inaonekana kwenye Kielelezo\(\PageIndex{10}\).
Weka equation\(4y^2−9x^2+16y+18x−29=0\) katika fomu ya kawaida na grafu hyperbola kusababisha. Je, ni equations ya asymptotes?
- Kidokezo
-
Hoja mara kwa mara juu na kukamilisha mraba. Angalia mwelekeo gani hyperbola inafungua
- Jibu
-
\(\dfrac{(y+2)^2}{9}−\dfrac{(x−1)^2}{4}=1.\)Hii ni hyperbola wima. Asymptotes\(y=−2±\dfrac{3}{2}(x−1).\)

Hyperbolas pia ina mali ya kutafakari ya kuvutia. Ray iliyoelekezwa kuelekea lengo moja la hyperbola inaonekana na kioo cha hyperbolic kuelekea lengo lingine. Dhana hii ni mfano katika Kielelezo\(\PageIndex{11}\).
Mali hii ya hyperbola ina maombi muhimu. Inatumika katika kutafuta mwelekeo wa redio (kwa kuwa tofauti katika ishara kutoka minara miwili ni mara kwa mara pamoja na hyperbolas), na katika ujenzi wa vioo ndani ya darubini (kutafakari mwanga kutoka kioo cha parabolic hadi kwenye jicho la macho). Ukweli mwingine wa kuvutia kuhusu hyperbolas ni kwamba kwa comet inayoingia kwenye mfumo wa jua, ikiwa kasi ni kubwa ya kutosha kuepuka mvuto wa Jua, basi njia ambayo comet inachukua inapita kupitia mfumo wa jua ni hyperbolic.
Eccentricity na Directrix
Njia mbadala ya kuelezea sehemu ya conic inahusisha maelekezo, foci, na mali mpya inayoitwa eccentricity. Tutaona kwamba thamani ya eccentricity ya sehemu conic inaweza kipekee kufafanua kwamba conic.
Uwezo wa sehemu \(e\)ya conic hufafanuliwa kuwa umbali kutoka kwa hatua yoyote kwenye sehemu ya conic kwa lengo lake, imegawanywa na umbali wa perpendicular kutoka hatua hiyo hadi directrix ya karibu. Thamani hii ni mara kwa mara kwa sehemu yoyote ya conic, na inaweza kufafanua sehemu ya conic pia:
- Ikiwa\(e=1\), conic ni parabola.
- Ikiwa\(e<1\), ni duaradufu.
- Ikiwa\(e>1,\) ni hyperbola.
Uwezo wa mduara ni sifuri. Directrix ya sehemu ya conic ni mstari ambao, pamoja na hatua inayojulikana kama lengo, hutumikia kufafanua sehemu ya conic. Hyperbolas na ellipses zisizo na mviringo zina maelekezo mawili na maelekezo mawili yanayohusiana. Parabolas na lengo moja na moja directrix.
Sehemu tatu za conic na maelekezo yao zinaonekana kwenye Kielelezo\(\PageIndex{12}\).
Kumbuka kutokana na ufafanuzi wa parabola kwamba umbali kutoka kwa hatua yoyote juu ya parabola kwa lengo ni sawa na umbali kutoka hatua hiyo kwa directrix. Kwa hiyo, kwa ufafanuzi, eccentricity ya parabola lazima 1. Ulinganisho wa maelekezo ya ellipse ya usawa ni\(x=±\dfrac{a^2}{c}\). Vertex sahihi ya ellipse iko\((a,0)\) na lengo sahihi ni\((c,0)\). Kwa hiyo, umbali kutoka vertex kwa lengo ni\(a−c\) na umbali kutoka vertex hadi directrix sahihi ni\(\dfrac{a^2}{c}−c.\) Hii inatoa eccentricity kama
\[e=\dfrac{a−c}{\dfrac{a^2}{c}−a}=\dfrac{c(a−c)}{a^2−ac}=\dfrac{c(a−c)}{a(a−c)}=\dfrac{c}{a}. \nonumber \]
Tangu\(c<a\), hatua hii inathibitisha kwamba eccentricity ya ellipse ni chini ya 1. Maelekezo ya hyperbola ya usawa pia iko\(x=±\dfrac{a^2}{c}\), na hesabu sawa inaonyesha kwamba uaminifu wa hyperbola pia ni\(e=\dfrac{c}{a}\). Hata hivyo katika kesi hii tuna\(c>a\), hivyo eccentricity ya hyperbola ni kubwa kuliko 1.
Kuamua eccentricity ya ellipse ilivyoelezwa na equation
\(\dfrac{(x−3)^2}{16}+\dfrac{(y+2)^2}{25}=1.\)
Suluhisho
Kutoka equation tunaona kwamba\(a=5\) na\(b=4\). Thamani ya c inaweza kuhesabiwa kwa kutumia equation\(a^2=b^2+c^2\) kwa ellipse. Kubadilisha maadili ya a na b na kutatua kwa c anatoa\(c=3\). Kwa hiyo, eccentricity ya ellipse ni\(e=\dfrac{c}{a}=\dfrac{3}{5}=0.6.\)
Kuamua eccentricity ya hyperbola ilivyoelezwa na equation
\(\dfrac{(y−3)^2}{49}−\dfrac{(x+2)^2}{25}=1.\)
- Kidokezo
-
Kwanza kupata maadili ya a na b, kisha kuamua c kutumia equation\(c^2=a^2+b^2\).
- Jibu
-
\(e=\dfrac{c}{a}=\dfrac{\sqrt{74}}{7}≈1.229\)
Ulinganisho wa Polar wa Sehemu za Conic
Wakati mwingine ni muhimu kuandika au kutambua usawa wa sehemu ya conic katika fomu ya polar. Ili kufanya hivyo, tunahitaji dhana ya parameter ya msingi. Kipimo cha msingi cha sehemu ya conic p hufafanuliwa kama umbali kutoka kwa lengo hadi directrix ya karibu. Jedwali linalofuata linatoa vigezo vya msingi kwa aina tofauti za conics, ambapo a ni urefu wa mhimili wa nusu kuu (yaani, nusu urefu wa mhimili mkubwa), c ni umbali kutoka kwa asili hadi lengo, na e ni eccentricity. Katika kesi ya parabola, a inawakilisha umbali kutoka vertex kwa lengo.
| Conic | \(e\) | \(p\) |
|---|---|---|
| duaradufu | \ (e\)” style="wima align:katikati; ">\(0<e<1\) | \ (p\)” style="wima align:katikati; ">\(\dfrac{a^2−c^2}{c}=\dfrac{a(1−e^2)}{c}\) |
| Parabola | \ (e\)” style="wima align:katikati; ">\(e=1\) | \ (p\)” style="wima align:katikati; ">\(2a\) |
| Hyperbola | \ (e\)” style="wima align:katikati; ">\(e>1\) | \ (p\)” style="wima align:katikati; ">\(\dfrac{c^2−a^2}{c}=\dfrac{a(e^2−1)}{c}\) |
Kutumia ufafanuzi wa parameter ya msingi na uwiano wa sehemu ya conic, tunaweza kupata equation kwa sehemu yoyote ya conic katika kuratibu polar. Hasa, tunadhani kwamba moja ya foci ya sehemu ya conic iliyotolewa iko kwenye pole. Kisha kutumia ufafanuzi wa sehemu mbalimbali za conic kwa suala la umbali, inawezekana kuthibitisha theorem ifuatayo.
Equation ya polar ya sehemu ya conic na parameter ya msingi p hutolewa na
\(r=\dfrac{ep}{1±e\cos θ}\)au\(r=\dfrac{ep}{1±e\sin θ}.\)
Katika equation upande wa kushoto, mhimili mkubwa wa sehemu ya conic ni usawa, na katika equation upande wa kulia, mhimili mkubwa ni wima. Kufanya kazi na sehemu ya conic iliyoandikwa kwa fomu ya polar, kwanza fanya muda wa mara kwa mara katika denominator sawa na 1. Hii inaweza kufanyika kwa kugawanya namba zote mbili na denominator ya sehemu kwa mara kwa mara inayoonekana mbele ya pamoja au minus katika denominator. Kisha mgawo wa sine au cosine katika denominator ni eccentricity. Thamani hii inatambua conic. Ikiwa cosine inaonekana katika denominator, basi conic ni ya usawa. Ikiwa sine inaonekana, basi conic ni wima. Ikiwa wote wanaonekana basi axes huzungushwa. Katikati ya conic sio lazima kwa asili. Kituo ni asili tu kama coniki ni mduara (yaani,\(e=0\)).
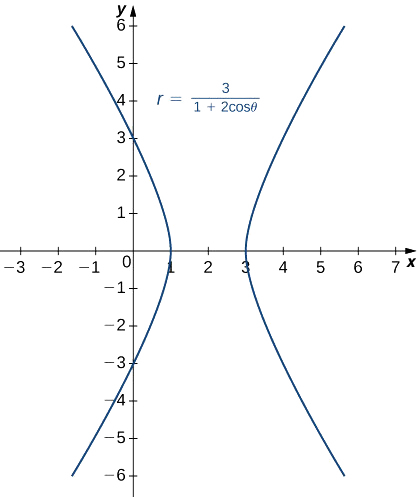
Tambua na uunda grafu ya sehemu ya conic iliyoelezwa na equation
\(r=\dfrac{3}{1+2\cos θ}\).
Suluhisho
Muda wa mara kwa mara katika denominator ni 1, hivyo eccentricity ya conic ni 2. Hii ni hyperbola. Kipimo cha msingi p kinaweza kuhesabiwa kwa kutumia equation\(ep=3.\) Tangu\(e=2\), hii inatoa\(p=\dfrac{3}{2}\). Kazi ya cosine inaonekana katika denominator, hivyo hyperbola ni ya usawa. Chagua maadili machache\(θ\) na uunda meza ya maadili. Kisha tunaweza grafu hyperbola (Kielelezo\(\PageIndex{13}\)).
| \(θ\) | \(r\) | \(θ\) | \(r\) |
|---|---|---|---|
| \ (坪\)” style="wima align:katikati; "> 0 | \ (r\)” style="wima align:katikati; "> 1 | \ (合\)” style="wima align:katikati; ">\(π\) | \ (r\)” style="wima align:katikati; "> -3 |
| \ (合\)” style="wima align:katikati; ">\(\dfrac{π}{4}\) | \ (r\)” style="wima align:katikati; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) | \ (合\)” style="wima align:katikati; ">\(\dfrac{5π}{4}\) | \ (r\)” style="wima align:katikati; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) |
| \ (合\)” style="wima align:katikati; ">\(\dfrac{π}{2}\) | \ (r\)” style="wima align:katikati; "> 3 | \ (合\)” style="wima align:katikati; ">\(\dfrac{3π}{2}\) | \ (r\)” style="wima align:katikati; "> 3 |
| \ (合\)” style="wima align:katikati; ">\(\dfrac{3π}{4}\) | \ (r\)” style="wima align:katikati; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) | \ (合\)” style="wima align:katikati; ">\(\dfrac{7π}{4}\) | \ (r\)” style="wima align:katikati; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) |
Tambua na uunda grafu ya sehemu ya conic iliyoelezwa na equation
\(r=\dfrac{4}{1−0.8 \sin θ}\).
- Kidokezo
-
Kwanza kupata maadili ya e na p, na kisha uunda meza ya maadili.
- Jibu
-
Hapa\(e=0.8\) na\(p=5\). Sehemu hii ya conic ni ellipse.
General equations ya Shahada mbili
Equation ya jumla ya shahada mbili inaweza kuandikwa kwa fomu
\[ Ax^2+Bxy+Cy^2+Dx+Ey+F=0. \nonumber \]
Grafu ya equation ya fomu hii ni sehemu ya conic. Ikiwa\(B≠0\) basi axes za kuratibu zimezungushwa. Ili kutambua sehemu ya conic, tunatumia ubaguzi wa sehemu ya conic\(4AC−B^2.\)
Moja ya kesi zifuatazo lazima iwe kweli:
- \(4AC−B^2>0\). Ikiwa ndivyo, grafu ni ellipse.
- \(4AC−B^2=0\). Ikiwa ndivyo, grafu ni parabola.
- \(4AC−B^2<0\). Ikiwa ndivyo, grafu ni hyperbola.
Mfano rahisi zaidi wa equation ya pili ya shahada inayohusisha muda wa msalaba ni\(xy=1\). equation Hii inaweza kutatuliwa\(y\) kwa kupata\(y=\dfrac{1}{x}\). Grafu ya kazi hii inaitwa hyperbola mstatili kama inavyoonekana.
Asymptotes ya hyperbola hii ni\(x\) na\(y\) kuratibu axes. Kuamua angle ya mzunguko wa sehemu ya conic, tunatumia formula\(\cot 2θ=\frac{A−C}{B}\). Katika kesi hii\(A=C=0\) na\(B=1\), hivyo\(\cot 2θ=(0−0)/1=0\) na\(θ=45°\). Njia ya kuchora sehemu ya conic na axes zinazozunguka inahusisha kuamua coefficients ya conic katika mfumo wa kuratibu unaozunguka. Coefficients mpya ni lebo\(A′,B′,C′,D′,E′,\)\(F′,\) na hutolewa na formula
\[ \begin{align} A′ =A\cos^ 2θ+B\cos θ\sin θ+C\sin^2 θ \\ B′ =0 \\ C′ =A\sin^2 θ−B\sin θ\cos θ+C\cos^2θ \\ D′ =D\cos θ+E\sin θ \\ E′ =−D\sin θ+E\cosθ \\ F′ =F. \end{align} \nonumber \]
Utaratibu wa kuchora conic iliyozungushwa ni yafuatayo:
- Tambua sehemu ya conic kwa kutumia ubaguzi\(4AC−B^2\).
- Tambua\(θ\) kutumia formula\[\cot2θ=\dfrac{A−C}{B} \label{rot}. \]
- Mahesabu\(A′,B′,C′,D′,E′\), na\(F′\).
- Andika upya equation awali kwa kutumia\(A′,B′,C′,D′,E′\), na\(F′\).
- Chora grafu kwa kutumia equation iliyozungushwa.
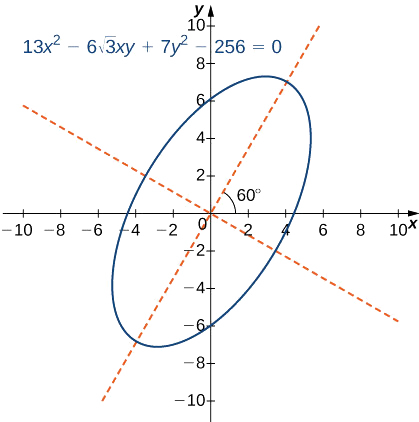
Tambua conic na uhesabu angle ya mzunguko wa axes kwa safu iliyoelezwa na equation
\[13x^2−6\sqrt{3}xy+7y^2−256=0. \nonumber \]
Suluhisho
Katika equation hii,\(A=13,B=−6\sqrt{3},C=7,D=0,E=0,\) na\(F=−256\). Wabaguzi wa equation hii ni
\[4AC−B^2=4(13)(7)−(−6\sqrt{3})^2=364−108=256. \nonumber \]
Kwa hiyo conic hii ni duaradufu.
Ili kuhesabu angle ya mzunguko wa axes, tumia Equation\ ref {kuoza}
\[\cot 2θ=\dfrac{A−C}{B}. \nonumber \]
Hii inatoa
\(\cot 2θ=\dfrac{A−C}{B}=\dfrac{13−7}{−6\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\).
Kwa hiyo\(2θ=120^o\) na\(θ=60^o\), ambayo ni angle ya mzunguko wa axes.
Kuamua coefficients kuzungushwa, tumia formula zilizotolewa hapo juu:
\(A′=A\cos^2θ+B\cos θ\sinθ+C\sin^2θ\)
\(=13\cos^260+(−6\sqrt{3})\cos 60 \sin 60+7\sin^260\)
\(=13(\dfrac{1}{2})^2−6\sqrt{3}(\dfrac{1}{2})(\dfrac{\sqrt{3}}{2})+7(\dfrac{\sqrt{3}}{2})^2\)
\(=4,\)
\(B′=0\)
\(C′=A\sin^2θ−B\sin θ\cos θ+C\cos^2θ\)
\(=13\sin^260+(6\sqrt{3})\sin 60 \cos 60+7\cos^260\)
\(=13(\dfrac{\sqrt{3}}{2})^2+6\sqrt{3}(\dfrac{\sqrt{3}}{2})(\dfrac{1}{2})+7(\dfrac{1}{2})^2\)
\(=16,\)
\(D′=D\cos θ+E\sin θ\)
\(=(0)\cos 60+(0)\sin 60\)
\(=0,\)
\(E′=−D\sin θ+E\cos θ\)
\(=−(0)\sin 60+(0)\cos 60\)
\(=0\)
\(F′= F\)
\(=−256.\)
Equation ya conic katika mfumo wa kuratibu unaozunguka inakuwa
\(4(x′)^2+16(y′)^2=256\)
\(\dfrac{(x′)^2}{64}+\dfrac{(y′)^2}{16}=1\).
Grafu ya sehemu hii ya conic inaonekana kama ifuatavyo.
Tambua conic na uhesabu angle ya mzunguko wa axes kwa safu iliyoelezwa na equation
\[3x^2+5xy−2y^2−125=0. \nonumber \]
- Kidokezo
-
Fuata hatua 1 na 2 za njia ya hatua tano iliyoelezwa hapo juu
- Jibu
-
Conic ni hyperbola na angle ya mzunguko wa axes ni\(θ=22.5°.\)
Dhana muhimu
- Ulinganisho wa parabola wima katika fomu ya kawaida na lengo lililopewa na directrix\(p\) ni\(y=\dfrac{1}{4p}(x−h)^2+k\) wapi umbali kutoka kipeo hadi kwenye lengo na\((h,k)\) ni kuratibu za kipeo.
- Ulinganisho wa duaradufu ya usawa katika fomu ya kawaida ni\(\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1\) ambapo kituo hicho kina kuratibu\((h,k)\), mhimili mkubwa una urefu wa 2a, mhimili mdogo una urefu wa 2b, na kuratibu za foci ni\((h±c,k)\) wapi\(c^2=a^2−b^2\).
- Equation ya hyperbola ya usawa katika fomu ya kawaida ni\(\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1\) ambapo kituo hicho\((h,k)\) kina kuratibu, vipeo viko\((h±a,k)\), na kuratibu za foci ni\((h±c,k),\) wapi\(c^2=a^2+b^2\).
- Eccentricity ya duaradufu ni chini ya 1, eccentricity ya parabola ni sawa na 1, na eccentricity ya hyperbola ni kubwa kuliko 1. Uwezo wa mduara ni 0.
- Equation ya polar ya sehemu ya conic na eccentricity e ni\(r=\dfrac{ep}{1±ecosθ}\) au\(r=\dfrac{ep}{1±esinθ}\), ambapo p inawakilisha parameter ya msingi.
- Ili kutambua conic yanayotokana na equation\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\), kwanza uhesabu ubaguzi\(D=4AC−B^2\). Ikiwa\(D>0\) basi conic ni ellipse, ikiwa\(D=0\) basi conic ni parabola, na kama\(D<0\) basi conic ni hyperbola.
faharasa
- sehemu ya conic
- sehemu ya conic ni safu yoyote iliyoundwa na makutano ya ndege yenye koni ya nappes mbili
- directrix
- directrix (wingi: maelekezo) ni mstari unaotumiwa kujenga na kufafanua sehemu ya conic; parabola ina directrix moja; ellipses na hyperbolas zina mbili
- kubagua
- thamani\(4AC−B^2\), ambayo hutumiwa kutambua conic wakati equation ina neno kuwashirikisha\(xy\), inaitwa ubaguzi
- lengo
- lengo (wingi: foci) ni hatua inayotumiwa kujenga na kufafanua sehemu ya conic; parabola ina lengo moja; ellipse na hyperbola zina mbili
- upotovu
- eccentricity hufafanuliwa kama umbali kutoka hatua yoyote juu ya sehemu conic kwa lengo lake kugawanywa na umbali perpendicular kutoka hatua hiyo kwa directrix karibu
- parameter ya msingi
- parameter ya msingi ni umbali kutoka kwa lengo la sehemu ya conic hadi directrix ya karibu
- fomu ya jumla
- equation ya sehemu conic iliyoandikwa kama jumla ya pili shahada equation
- mhimili mkubwa
- mhimili mkubwa wa sehemu ya conic hupita kupitia vertex katika kesi ya parabola au kupitia vertices mbili katika kesi ya ellipse au hyperbola; pia ni mhimili wa ulinganifu wa conic; pia huitwa mhimili wa transverse
- mhimili mdogo
- mhimili mdogo ni perpendicular kwa mhimili mkubwa na intersects mhimili kuu katikati ya conic, au kwenye vertex katika kesi ya parabola; pia huitwa mhimili wa conjugate
- nappe
- nappe ni nusu moja ya koni mbili
- fomu ya kawaida
- usawa wa sehemu ya conic inayoonyesha mali zake, kama eneo la vertex au urefu wa shoka kuu na ndogo
- vertex
- vertex ni hatua kali juu ya sehemu ya conic; parabola ina vertex moja katika hatua yake ya kugeuka. Elipse ina vertices mbili, moja kila mwisho wa mhimili mkuu; hyperbola ina vipeo viwili, moja katika hatua ya kugeuka ya kila tawi


