11.3: Kuratibu Polar
- Page ID
- 178445
- Pata pointi katika ndege kwa kutumia viwianishi vya polar.
- Badilisha pointi kati ya kuratibu mstatili na polar.
- Mchoro wa polar curves kutoka kwa usawa uliopewa.
- Badilisha equations kati ya kuratibu mstatili na polar.
- Kutambua ulinganifu katika curves polar na equations.
Mfumo wa kuratibu mstatili (au ndege ya Cartesian) hutoa njia za pointi za ramani kwa jozi zilizoamriwa na kuamuru jozi kwa pointi. Hii inaitwa ramani moja kwa moja kutoka kwa pointi katika ndege hadi jozi zilizoamriwa. Mfumo wa kuratibu polar hutoa njia mbadala ya pointi za ramani kwa jozi zilizoamriwa. Katika sehemu hii tunaona kwamba katika hali fulani, kuratibu polar inaweza kuwa muhimu zaidi kuliko kuratibu mstatili.
Kufafanua Kuratibu Polar
Ili kupata kuratibu za uhakika katika mfumo wa kuratibu polar, fikiria Kielelezo\(\PageIndex{1}\). Hatua\(P\) ina kuratibu za Cartesian\((x,y)\). Sehemu ya mstari inayounganisha asili hadi\(P\) hatua inachukua umbali kutoka kwa asili\(P\) na ina urefu\(r\). Pembe kati ya x-axis chanya na sehemu ya mstari ina kipimo\(θ\). Uchunguzi huu unaonyesha mawasiliano ya asili kati ya jozi\((x,y)\) ya kuratibu\(r\) na maadili na\(θ\). Mawasiliano hii ni msingi wa mfumo wa kuratibu polar. Kumbuka kwamba kila hatua katika ndege ya Cartesian ina maadili mawili (kwa hiyo neno lililoamriwa jozi) linalohusishwa nayo. Katika mfumo wa kuratibu polar, kila hatua pia ina maadili mawili yanayohusiana nayo:\(r\) na\(θ\).
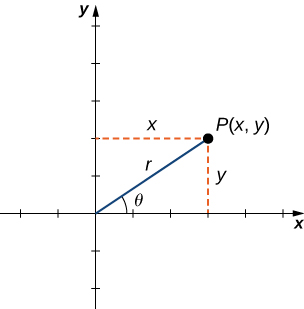
Kutumia trigonometry ya pembetatu ya kulia, equations zifuatazo ni kweli kwa uhakika\(P\):
\[\cos θ=\dfrac{x}{r}\text{ so }x=r\cos θ \nonumber \]
\[\sin θ=\dfrac{y}{r}\text{ so }y=r\sin θ. \nonumber \]
Aidha,
\[r^2=x^2+y^2 \nonumber \]
na
\[\tan θ=\dfrac{y}{x}. \nonumber \]
Kila hatua\((x,y)\) katika mfumo wa kuratibu wa Cartesian inaweza kuwakilishwa kama jozi iliyoamriwa\((r,θ)\) katika mfumo wa kuratibu polar. Kuratibu ya kwanza inaitwa kuratibu radial na kuratibu ya pili inaitwa kuratibu angular. Kila hatua katika ndege inaweza kuwakilishwa katika fomu hii.
Kumbuka kuwa equation\(\tan θ=y/x\) ina idadi isiyo na mwisho ya ufumbuzi kwa jozi yoyote iliyoamriwa\((x,y)\). Hata hivyo, ikiwa tunazuia ufumbuzi wa maadili kati\(0\) na\(2π\) kisha tunaweza kugawa suluhisho la kipekee kwa quadrant ambayo hatua ya awali\((x,y)\) iko. Kisha thamani sambamba ya\(r\) ni chanya, hivyo\(r^2=x^2+y^2\).
Kutokana na hatua\(P\) katika ndege na kuratibu za Cartesian\((x,y)\) na kuratibu za polar\((r,θ)\), kanuni zifuatazo za uongofu zinashikilia kweli:
\[\begin{align} x &=r\cos θ \label{eq1} \\[4pt] y &=r\sin θ \label{eq2}\end{align} \]
na
\[\begin{align} r^2 &= x^2+y^2 \label{eq3}\\[4pt] \tan θ &=\dfrac{y}{x} \label{eq4}\end{align}. \]
Njia hizi zinaweza kutumika kubadili kutoka mstatili hadi polar au kutoka polar hadi kuratibu mstatili. Angalia kwamba Equation\ ref {eq3} ni theorem ya Pythagorean. (Kielelezo\(\PageIndex{1}\)).
Badilisha kila moja ya pointi zifuatazo katika kuratibu polar.
- \((1,1)\)
- \((−3,4)\)
- \((0,3)\)
- \((5\sqrt{3},−5)\)
Badilisha kila moja ya pointi zifuatazo katika kuratibu mstatili.
- \((3,π/3)\)
- \((2,3π/2)\)
- \((6,−5π/6)\)
Suluhisho
a. Matumizi\(x=1\) na\(y=1\) katika Equation\ ref {eq3}:
\[\begin{align*} r^2 &=x^2+y^2 \\[4pt] &=1^2+1^2 \\ r &=\sqrt{2} \end{align*} \nonumber \]
na kupitia Equation\ ref {eq4}
\[\begin{align*} \tan θ &= \dfrac{y}{x} = \dfrac{1}{1}=1 \\[4pt] θ &=\dfrac{π}{4}. \end{align*}\]
Kwa hiyo hatua hii inaweza kuwakilishwa kama\((\sqrt{2},\dfrac{π}{4})\) katika kuratibu polar.
b. matumizi\(x=−3\) na\(y=4\) katika Equation\ ref {eq3}:
\[\begin{align*} r^2 &= x^2+y^2=(−3)^2+(4)^2 \\[4pt] r&=5 \end{align*}\]
na kupitia Equation\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=−\dfrac{4}{3}\)
\(θ=\arctan(-\dfrac{4}{3})+π≈2.21.\)
Kwa hiyo hatua hii inaweza kuwakilishwa kama\((5,2.21)\) katika kuratibu polar.
c Matumizi\(x=0\) na\(y=3\) katika Equation\ ref {eq3}:
\(r^2=x^2+y^2=(3)^2+(0)^2=9+0\)\(r=3\)
na kupitia Equation\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{3}{0}\).
Matumizi ya moja kwa moja ya equation ya pili inaongoza kwa mgawanyiko na sifuri. Kuchunguza hatua\((0,3)\) kwenye mfumo wa kuratibu mstatili unaonyesha kwamba hatua iko kwenye mhimili wa y mzuri. Pembe kati ya x-axis chanya na chanya y-axis ni\(\dfrac{π}{2}\). Kwa hiyo hatua hii inaweza kuwakilishwa kama\((3,\dfrac{π}{2})\) katika kuratibu polar.
d. matumizi\(x=5\sqrt{3}\) na\(y=−5\) katika Equation\ ref {eq3}:
\(r^2=x^2+y^2=(5\sqrt{3})^2+(−5)^2=75+25\)
\(r=10\)
na kupitia Equation\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{−5}{5\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\)
\(θ=−\dfrac{π}{6}\).
Kwa hiyo hatua hii inaweza kuwakilishwa kama\((10,−\dfrac{π}{6})\) katika kuratibu polar.
e Matumizi\(r=3\) na\(θ=\dfrac{π}{3}\) katika Equation\ ref {eq1}:
\(x=r\cos θ=3\cos(\dfrac{π}{3})=3(\dfrac{1}{2})=\dfrac{3}{2}\)
na
\(y=r\sin θ=3\sin(\dfrac{π}{3})=3(\dfrac{\sqrt{3}}{2})=\dfrac{3\sqrt{3}}{2}\).
Kwa hiyo hatua hii inaweza kuwakilishwa kama\((\dfrac{3}{2},\dfrac{3\sqrt{3}}{2})\) katika kuratibu mstatili.
f. Matumizi\(r=2\) na\(θ=\dfrac{3π}{2}\) katika Equation\ ref {eq1}:
\(x=r\cos θ=2\cos(\dfrac{3π}{2})=2(0)=0\)
na
\(y=r\sin θ=2\sin(\dfrac{3π}{2})=2(−1)=−2.\)
Kwa hiyo hatua hii inaweza kuwakilishwa kama\((0,−2)\) katika kuratibu mstatili.
g. matumizi\(r=6\) na\(θ=−\dfrac{5π}{6}\) katika Equation\ ref {eq1}:
\(x=r\cos θ=6\cos(−\dfrac{5π}{6})=6(−\dfrac{\sqrt{3}}{2})=−3\sqrt{3}\)
na
\(y=r\sin θ=6\sin(−\dfrac{5π}{6})=6(−\dfrac{1}{2})=−3\).
Kwa hiyo hatua hii inaweza kuwakilishwa kama\((−3\sqrt{3},−3)\) katika kuratibu mstatili.
Badilisha\((−8,−8)\) katika kuratibu za polar na\((4,\dfrac{2π}{3})\) uratibu wa mstatili.
- Kidokezo
-
Tumia Equation\ ref {eq3} na Equation\ ref {eq1}. Hakikisha kuangalia quadrant wakati wa kuhesabu\(θ\).
- Jibu
-
\((8\sqrt{2},\dfrac{5π}{4})\)na\((−2,2\sqrt{3})\)
Uwakilishi wa polar wa uhakika sio wa kipekee. Kwa mfano, kuratibu polar\((2,\dfrac{π}{3})\) na\((2,\dfrac{7π}{3})\) wote wanawakilisha hatua\((1,\sqrt{3})\) katika mfumo wa mstatili. Pia, thamani ya r inaweza kuwa hasi. Kwa hiyo, hatua na kuratibu polar\((−2,\dfrac{4π}{3})\) pia inawakilisha hatua\((1,\sqrt{3})\) katika mfumo wa mstatili, kama tunavyoweza kuona kwa kutumia Equation\ ref {eq1}:
\[x=r\cos θ=−2\cos(\dfrac{4π}{3})=−2(−\dfrac{1}{2})=1 \nonumber \]
na
\[y=r\sin θ=−2\sin(\dfrac{4π}{3})=−2(−\dfrac{\sqrt{3}}{2})=\sqrt{3}. \nonumber \]
Kila hatua katika ndege ina idadi isiyo na mwisho ya uwakilishi katika kuratibu polar. Hata hivyo, kila hatua katika ndege ina uwakilishi mmoja tu katika mfumo wa kuratibu mstatili.
Kumbuka kuwa uwakilishi wa polar wa hatua katika ndege pia una tafsiri ya kuona. Hasa,\(r\) ni umbali ulioongozwa kwamba hatua hiyo iko kutoka kwa asili, na\(θ\) hupima angle ambayo sehemu ya mstari kutoka kwa asili hadi hatua hufanya na\(x\) mhimili mzuri. Pembe nzuri hupimwa kwa mwelekeo wa kinyume na pembe hasi hupimwa kwa mwelekeo wa saa. Mfumo wa kuratibu wa polar unaonekana kwenye Kielelezo\(\PageIndex{2}\).
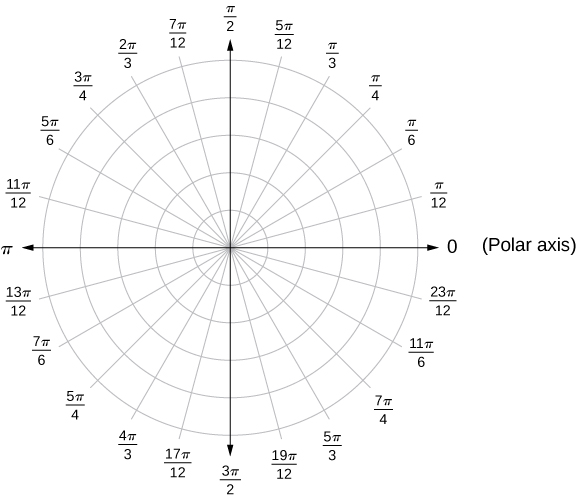
Sehemu ya mstari kuanzia katikati ya grafu kwenda kulia (inayoitwa x-axis chanya katika mfumo wa Cartesian) ni mhimili wa polar. Kituo cha katikati ni pole, au asili, ya mfumo wa kuratibu, na inafanana na\(r=0\). mduara ndani inavyoonekana katika Kielelezo\(\PageIndex{2}\) ina pointi zote umbali wa 1 kitengo kutoka pole, na ni kuwakilishwa na equation\(r=1\). Kisha\(r=2\) ni seti ya pointi 2 vitengo kutoka pole, na kadhalika. Makundi ya mstari yanayotokana na pole yanahusiana na pembe za kudumu. Ili kupanga mpango katika mfumo wa kuratibu polar, kuanza kwa angle. Ikiwa angle ni chanya, kisha kupima angle kutoka kwa mhimili wa polar kwa mwelekeo wa kinyume. Ikiwa ni hasi, kisha uipime saa moja kwa moja. Ikiwa thamani ya r ni chanya, songa umbali huo pamoja na ray ya terminal ya angle. Ikiwa ni hasi, songa pamoja na ray ambayo ni kinyume na ray terminal ya angle iliyotolewa.
Panda kila moja ya pointi zifuatazo kwenye ndege ya polar.
- \((2,\dfrac{π}{4})\)
- \((−3,\dfrac{2π}{3})\)
- \((4,\dfrac{5π}{4})\)
Suluhisho
pointi tatu ni njama katika Kielelezo\(\PageIndex{3}\).

Panda\((4,\dfrac{5π}{3})\) na\((−3,−\dfrac{7π}{2})\) kwenye ndege ya polar.
- Kidokezo
-
Anza na\(θ\), kisha utumie\(r\).
- Jibu
-

polar curves
Sasa kwa kuwa tunajua jinsi ya kupanga njama katika mfumo wa kuratibu polar, tunaweza kujadili jinsi ya kupanga njama. Katika mfumo wa kuratibu mstatili, tunaweza kuchora kazi\(y=f(x)\) na kuunda safu katika ndege ya Cartesian. Kwa mtindo sawa, tunaweza graph Curve kwamba ni yanayotokana na kazi\(r=f(θ)\).
Wazo la jumla nyuma ya kuchora kazi katika kuratibu polar ni sawa na kuchora kazi katika kuratibu mstatili. Anza na orodha ya maadili kwa kutofautiana kwa kujitegemea (\(θ\)katika kesi hii) na uhesabu maadili yanayofanana ya kutofautiana kwa tegemezi\(r\). Utaratibu huu huzalisha orodha ya jozi zilizoamriwa, ambazo zinaweza kupangwa katika mfumo wa kuratibu polar. Hatimaye, kuunganisha pointi, na kuchukua faida ya mifumo yoyote ambayo inaweza kuonekana. Kazi inaweza kuwa mara kwa mara, kwa mfano, ambayo inaonyesha kwamba idadi ndogo tu ya maadili kwa kutofautiana kwa kujitegemea inahitajika.
- Unda meza na nguzo mbili. Safu ya kwanza ni ya\(θ\), na safu ya pili ni kwa\(r\).
- Unda orodha ya maadili kwa\(θ\).
- Tumia\(r\) maadili yanayofanana kwa kila mmoja\(θ\).
- Panda kila jozi iliyoamriwa\((r,θ)\) kwenye safu za kuratibu.
- Unganisha pointi na uangalie mfano.
Graph Curve inavyoelezwa na kazi\(r=4\sin θ\). Tambua safu na uandike upya equation katika kuratibu mstatili.
Suluhisho
Kwa sababu kazi ni nyingi ya kazi sine, ni mara kwa mara na kipindi\(2π\), hivyo kutumia maadili kwa\(θ\) kati\(0\) na\(2π\). Matokeo ya hatua 1—3 yanaonekana katika meza ifuatayo. Kielelezo\(\PageIndex{4}\) kinaonyesha grafu kulingana na meza hii.
| \(θ\) | \(r=4\sin θ\) | \(θ\) | \(r=4\sin θ\) |
|---|---|---|---|
| \ (ρ\)” style="wima align:katikati; "> 0 | \ (r=4\ sin ρ\)” style="wima align:middle; "> 0 | \ (ρ\)” style="wima align:katikati; ">\(π\) | \ (r=4\ sin ρ\)” style="wima align:middle; "> 0 |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{π}{6}\) | \ (r=4\ sin ρ\)” style="wima align:middle; "> 2 | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{7π}{6}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(-2\) |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{π}{4}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(2\sqrt{2}≈2.8\) | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{5π}{4}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(−2\sqrt{2}≈−2.8\) |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{π}{3}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(2\sqrt{3}≈3.4\) | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{4π}{3}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(−2\sqrt{3}≈−3.4\) |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{π}{2}\) | \ (r=4\ sin ρ\)” style="wima align:middle; "> 4 | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{3π}{2}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(-4\) |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{2π}{3}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(2\sqrt{3}≈3.4\) | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{5π}{3}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(−2\sqrt{3}≈−3.4\) |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{3π}{4}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(2\sqrt{2}≈2.8\) | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{7π}{4}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">\(−2\sqrt{2}≈−2.8\) |
| \ (ρ\)” style="wima align:katikati; ">\(\dfrac{5π}{6}\) | \ (r=4\ sin ρ\)” style="wima align:middle; "> 2 | \ (ρ\)” style="wima align:katikati; ">\(\dfrac{11π}{6}\) | \ (r=4\ sin ρ\)” style="wima align:middle; ">-1 2 |
| \ (ρ\)” style="wima align:katikati; "> | \ (r=4\ sin ρ\)” style="wima align:middle; "> | \ (ρ\)” style="wima align:katikati; ">\(2π\) | \ (r=4\ sin ρ\)” style="wima align:middle; "> 0 |
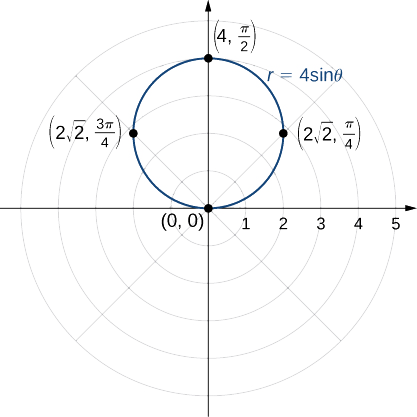
Hii ni grafu ya mduara. Equation\(r=4\sin θ\) inaweza kubadilishwa katika kuratibu mstatili na kwanza kuzidisha pande zote mbili na\(r\). Hii inakupa equation\(r^2=4r\sin θ.\) Next kutumia ukweli kwamba\(r^2=x^2+y^2\) na\(y=r\sin θ\). Hii inatoa\(x^2+y^2=4y\). Ili kuweka equation hii katika fomu ya kawaida, Ondoa\(4y\) kutoka pande zote mbili za equation na ukamilisha mraba:
\[\begin{align*} x^2+y^2−4y &= 0 \\[4pt] x^2+(y^2−4y) &= 0 \\[4pt] x^2+(y^2−4y+4) &= 0+4 \\[4pt] x^2+(y−2)^2&=4 \end{align*}\]
Hii ni equation ya mduara na radius 2 na katikati\((0,2)\) katika mfumo wa kuratibu mstatili.
Unda grafu ya safu iliyofafanuliwa na kazi\(r=4+4\cos θ\).
- Kidokezo
-
Fuata mkakati wa kutatua matatizo kwa ajili ya kujenga grafu katika kuratibu za polar.
- Jibu
-
Jina la sura hii ni cardioid, ambayo tutajifunza baadaye katika sehemu hii.
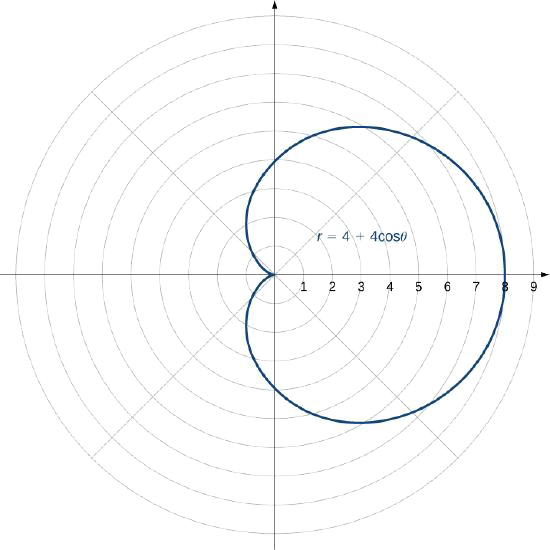
Grafu katika Mfano\(\PageIndex{3}\) ilikuwa ile ya mduara. Ulinganisho wa mduara unaweza kubadilishwa kuwa kuratibu mstatili kwa kutumia formula za mabadiliko ya kuratibu katika Equation\ ref {eq1}. Mfano\(\PageIndex{4}\) hutoa mifano zaidi ya kazi za kubadilisha kutoka polar hadi kuratibu mstatili.
Andika upya kila moja ya equations zifuatazo katika kuratibu mstatili na kutambua grafu.
- \(θ=\dfrac{π}{3}\)
- \(r=3\)
- \(r=6\cos θ−8\sin θ\)
Suluhisho:
Chukua tangent ya pande zote mbili. Hii\(\tan θ=\tan(π/3)=\sqrt{3}\)\(\tan θ=y/x\) inakupa.Tangu tunaweza kuchukua nafasi ya upande wa kushoto wa equation hii na\(y/x\). Hii inatoa\(y/x=\sqrt{3}\), ambayo inaweza kuandikwa upya kama\(y=x\sqrt{3}\). Hii ni equation ya mstari wa moja kwa moja unaopitia asili na mteremko\(\sqrt{3}\). Kwa ujumla, equation yoyote ya polar ya fomu\(θ=K\) inawakilisha mstari wa moja kwa moja kupitia pole na mteremko sawa na\(\tan K\).
b Kwanza, mraba pande zote mbili za equation. Hii inakupa\(r^2=9.\) Next kuchukua nafasi\(r^2\) kwa\(x^2+y^2\). Hii inatoa equation\(x^2+y^2=9\), ambayo ni equation ya mduara unaozingatia katika asili na radius 3. Kwa ujumla, equation yoyote ya polar ya fomu\(r=k\) ambapo k ni mara kwa mara chanya inawakilisha mduara wa radius k unaozingatia asili. (Kumbuka: wakati wa mraba pande zote mbili za equation inawezekana kuanzisha pointi mpya bila kukusudia. Hii inapaswa kuzingatiwa daima. Hata hivyo, katika kesi hii hatuwezi kuanzisha pointi mpya. Kwa mfano,\((−3,\dfrac{π}{3})\) ni hatua sawa na\((3,\dfrac{4π}{3})\).)
c. kuzidisha pande zote mbili za equation na\(r\). Hii inasababisha\(r^2=6r\cos θ−8r\sin θ\). Next kutumia formula
\(r^2=x^2+y^2,x=r\cos θ,y=r\sin θ.\)
Hii inakupa
\(r^2=6(r\cos θ)−8(r\sin θ)\)
\(x^2+y^2=6x−8y.\)
Ili kuweka equation hii katika fomu ya kawaida, kwanza hoja vigezo kutoka upande wa kulia wa equation kwa upande wa kushoto, kisha kukamilisha mraba.
\(x^2+y^2=6x−8y\)
\(x^2−6x+y^2+8y=0\)
\((x^2−6x)+(y^2+8y)=0\)
\((x^2−6x+9)+(y^2+8y+16)=9+16\)
\((x−3)^2+(y+4)^2=25.\)
Hii ni equation ya mduara na kituo cha saa\((3,−4)\) na Radius 5. Ona kwamba mduara unapitia asili tangu kituo hicho kina umbali wa vitengo 5.
Andika upya equation\(r=\sec θ\tan θ\) katika kuratibu mstatili na kutambua grafu yake.
- Kidokezo
-
Badilisha kwa sine na cosine, kisha kuzidisha pande zote mbili na cosine.
- Jibu
-
\(y=x^2\), ambayo ni equation ya parabola kufungua zaidi.
Sasa tumeona mifano kadhaa ya kuchora grafu ya curves inavyoelezwa na milinganyo ya polar. Muhtasari wa curves baadhi ya kawaida hutolewa katika meza hapa chini. Katika kila equation, a na b ni mara kwa mara ya kiholela.
Cardioid ni kesi maalum ya limaçon (inayojulikana “lee-mah-son”), ambayo\(a=b\) au\(a=−b\). Rose ni kama Curve ya kuvutia sana. Kumbuka kwamba grafu ya\(r=3\sin 2θ\) ina petals nne. Hata hivyo, grafu ya\(r=3\sin 3θ\) ina petals tatu kama inavyoonekana.
Ikiwa mgawo wa\(θ\) ni hata, grafu ina petals mara mbili kama mgawo. Ikiwa mgawo wa\(θ\) ni isiyo ya kawaida, basi idadi ya petals ni sawa na mgawo. Unahimizwa kuchunguza kwa nini hii inatokea. Grafu za kuvutia zaidi zinajitokeza wakati mgawo wa\(θ\) sio integer. Kwa mfano, ikiwa ni busara, basi safu imefungwa; yaani, hatimaye inaisha ambapo ilianza (Kielelezo\(\PageIndex{8a}\)). Hata hivyo, ikiwa mgawo hauna maana, basi safu haifai kamwe (Kielelezo\(\PageIndex{8b}\)). Ingawa inaweza kuonekana kwamba curve imefungwa, uchunguzi wa karibu unaonyesha kwamba petals tu juu ya mhimili x chanya ni kidogo mnene. Hii ni kwa sababu petal haifani kabisa na hatua ya mwanzo.
Tangu Curve inavyoelezwa na grafu ya\(r=3\sin(πθ)\) kamwe kufunga, Curve taswira katika Kielelezo\(\PageIndex{8b}\) ni tu depiction sehemu. Kwa kweli, hii ni mfano wa safu ya kujaza nafasi. Curve ya kujaza nafasi ni moja ambayo kwa kweli inachukua subset mbili-dimensional ya ndege halisi. Katika kesi hii curve inachukua mduara wa radius 3 unaozingatia asili.
Kumbuka nautilus iliyowekwa iliyoletwa katika sura ya utangulizi. Kiumbe hiki kinaonyesha ond wakati nusu ya ganda la nje limekatwa. Inawezekana kuelezea ond kwa kutumia kuratibu mstatili. Kielelezo\(\PageIndex{9}\) kinaonyesha ond katika kuratibu mstatili. Tunawezaje kuelezea Curve hii hesabu?
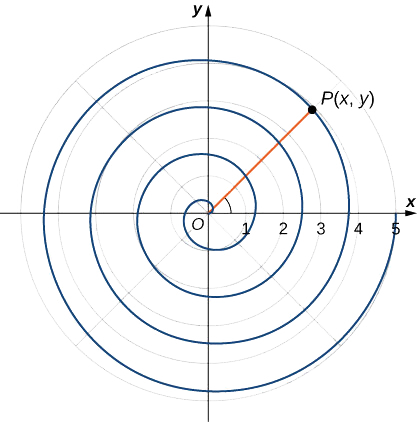
Suluhisho
Kama hatua P inazunguka ond katika mwelekeo kinyume, umbali wake d kutoka asili huongezeka. Fikiria kwamba umbali d ni k mara kwa mara nyingi ya angle\(θ\) ambayo sehemu ya mstari OP hufanya na chanya x-axis. Kwa hiyo\(d(P,O)=kθ\),\(O\) ni wapi asili. Sasa tumia formula ya umbali na trigonometry fulani:
\(d(P,O)=kθ\)
\(\sqrt{(x−0)^2+(y−0)^2}=k\arctan(\dfrac{y}{x})\)
\(\sqrt{x^2+y^2}=k\arctan(\dfrac{y}{x})\)
\(\arctan(\dfrac{y}{x})=\dfrac{\sqrt{x^2+y^2}}{k}\)
\(y=x\tan(\dfrac{\sqrt{x^2+y^2}}{k})\).
Ingawa equation hii inaelezea ond, haiwezekani kutatua moja kwa moja kwa ama x au y Hata hivyo, ikiwa tunatumia viwianishi vya polar, equation inakuwa rahisi sana. Hasa,\(d(P,O)=r\), na\(θ\) ni kuratibu pili. Kwa hiyo equation kwa ond inakuwa\(r=kθ\). Kumbuka kwamba wakati\(θ=0\) sisi pia tuna\(r=0\), hivyo ond inatoka kutoka asili. Tunaweza kuondoa kizuizi hiki kwa kuongeza mara kwa mara kwa equation. Kisha equation kwa ond inakuwa\(r=a+kθ\) kwa constants holela\(a\) na\(k\). Hii inajulikana kama ond Archimedean, baada ya Kigiriki hisabati Archimedes.
Aina nyingine ya ond ni ond logarithmic, ilivyoelezwa na kazi\(r=a⋅b^θ\). Grafu ya kazi\(r=1.2(1.25^θ)\) inatolewa katika Kielelezo\(\PageIndex{10}\). Spiral hii inaelezea sura ya shell ya nautilus iliyopangwa.
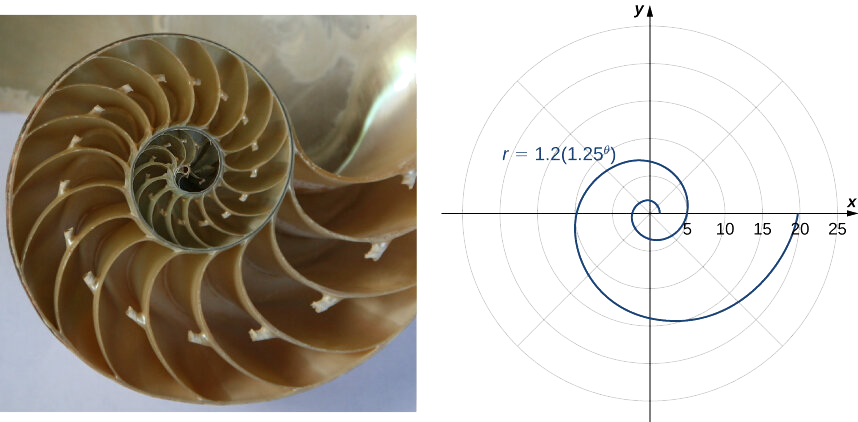
Tuseme curve inaelezwa katika mfumo wa kuratibu polar kupitia kazi\(r=f(θ)\). Kwa kuwa tuna uongofu formula kutoka polar kwa kuratibu mstatili iliyotolewa na
\[x=r\cos θ \nonumber \]
\[y=r\sin θ \nonumber \],
inawezekana kuandika upya fomu hizi kwa kutumia kazi
\[x=f(θ)\cos θ \nonumber \]
\[y=f(θ)\sin θ. \nonumber \]
Hatua hii inatoa parameterization ya curve katika kuratibu mstatili kutumia\(θ\) kama parameter. Kwa mfano, formula ya ond\(r=a+bθ\) kutoka Kielelezo inakuwa
\[x=(a+bθ)\cos θ \nonumber \]
\[y=(a+bθ)\sin θ. \nonumber \]
Kuruhusu\(θ\) mbalimbali kutoka\(−∞\) kwa\(∞\) kuzalisha ond nzima.
Ulinganifu katika Kuratibu Polar
Wakati wa kusoma ulinganifu wa kazi katika kuratibu za mstatili (yaani, kwa fomu\(y=f(x)\)), tunazungumzia kuhusu ulinganifu kwa heshima na y -axis na ulinganifu kwa heshima na asili. Hasa, ikiwa\(f(−x)=f(x)\) kwa wote\(x\) katika uwanja wa\(f\), basi\(f\) ni kazi hata na grafu yake ni sawa na heshima na y -axis. Ikiwa\(f(−x)=−f(x)\) kwa wote x katika uwanja wa\(f\), basi f ni kazi isiyo ya kawaida na grafu yake ni sawa na heshima na asili. Kwa kuamua aina gani za ulinganifu unaoonyesha grafu, tunaweza kujifunza zaidi kuhusu sura na kuonekana kwa grafu. Ulinganifu unaweza pia kufunua mali nyingine za kazi inayozalisha grafu. Ulinganifu katika curves polar hufanya kazi kwa mtindo sawa.
Fikiria Curve yanayotokana na kazi\(r=f(θ)\) katika kuratibu polar.
- Curve ni sawa kuhusu mhimili wa polar ikiwa kwa kila hatua\((r,θ)\) kwenye grafu, hatua pia\((r,−θ)\) iko kwenye grafu. Vile vile, equation\(r=f(θ)\) haibadilishwa kwa kuchukua nafasi\(θ\) na\(−θ\).
- Curve ni sawa juu ya pole ikiwa kwa kila hatua\((r,θ)\) kwenye grafu, hatua pia\((r,π+θ)\) iko kwenye grafu. Vile vile, equation\(r=f(θ)\) haibadilishwa wakati wa kuchukua nafasi\(r\)\(θ\) na\(−r\), au\(π+θ.\)
- Curve ni sawa na mstari wa wima\(θ=\dfrac{π}{2}\) ikiwa kwa kila hatua\((r,θ)\) kwenye grafu, hatua pia\((r,π−θ)\) iko kwenye grafu. Vile vile, equation\(r=f(θ)\) haibadilishwa wakati\(θ\) inabadilishwa na\(π−θ\).
Jedwali lifuatalo linaonyesha mifano ya kila aina ya ulinganifu.
Kupata ulinganifu wa rose defined na equation\(r=3\sin(2θ)\) na kujenga grafu.
Suluhisho
Tuseme uhakika\((r,θ)\) ni juu ya grafu ya\(r=3\sin(2θ).\)
i Ili kupima ulinganifu kuhusu mhimili wa polar, jaribu kwanza kuchukua nafasi\(θ\) na\(−θ\). Hii inatoa\(r=3\sin(2(−θ))=−3\sin(2θ)\). Kwa kuwa hii inabadilisha equation ya awali, mtihani huu haujaridhika. Hata hivyo, kurudi equation awali na kuchukua nafasi\(r\) na\(−r\)\(θ\) na kwa\(π−θ\) mavuno
\[ \begin{align*} −r&=3\sin(2(π−θ)) \\[4pt] −r &=3\sin(2π−2θ) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3\sin2θ. \end{align*}\]
Kuzidisha pande zote mbili za equation hii na\(−1\) anatoa\(r=3\sin 2θ\), ambayo ni equation awali. Hii inaonyesha kwamba grafu ni sawa na heshima na mhimili wa polar.
ii. Ili kupima ulinganifu kwa heshima na pole, kwanza kuchukua nafasi\(r\) na\(−r\), ambayo huzaa\(−r=3\sin(2θ)\). Kuzidisha pande zote mbili kwa\(−1\) kutoa\(r=−3\sin(2θ)\), ambayo haikubaliani na equation ya awali. Kwa hiyo equation haina kupita mtihani kwa ulinganifu huu. Hata hivyo, kurudi equation awali na kuchukua nafasi\(θ\) na\(θ+π\) anatoa
\[ \begin{align*} r&=3\sin(2(θ+π)) \\[4pt] &=3\sin(2θ+2π) \\[4pt] &=3(\sin 2θ \cos 2π + \cos 2θ \sin 2π) \\[4pt] &=3\sin 2θ. \end{align*}\]
Kwa kuwa hii inakubaliana na equation ya awali, grafu ni sawa na pole.
iii. Ili kupima ulinganifu kwa heshima na mstari wa wima\(θ=\dfrac{π}{2}\), kwanza uweke nafasi zote mbili\(r\)\(−r\)\(θ\) na\(−θ\).
\[ \begin{align*} −r &=3\sin(2(−θ)) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3 \sin 2θ. \end{align*}\]
Kuzidisha pande zote mbili za equation hii na\(−1\) anatoa\(r=3\sin 2θ\), ambayo ni equation awali. Kwa hiyo grafu ni sawa na mstari wa wima\(θ=\dfrac{π}{2}\).
Grafu hii ina ulinganifu kwa heshima na mhimili wa polar, asili, na mstari wa wima unaopitia pole. Ili grafu ya kazi, weka maadili ya\(θ\) kati\(0\)\(π/2\) na kisha kutafakari grafu inayosababisha.
| 0 | 0 |
| \(\dfrac{π}{6}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{4}\) | 3 |
| \(\dfrac{π}{3}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{2}\) | 0 |
Hii inatoa petal moja ya rose, kama inavyoonekana katika grafu ifuatayo.
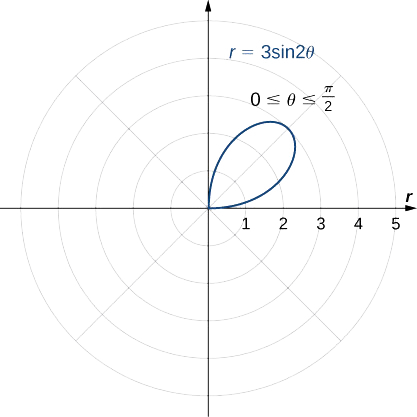
Kuonyesha picha hii katika quadrants nyingine tatu inatoa grafu nzima kama inavyoonekana.
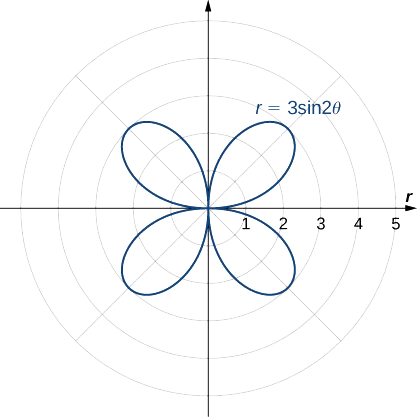
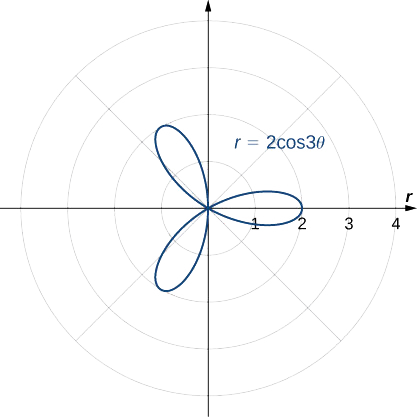
Kuamua ulinganifu wa grafu iliyowekwa na equation\(r=2\cos(3θ)\) na kuunda grafu.
- Kidokezo
-
Tumia Kumbuka.
- Jibu
-
Symmetric kwa heshima na mhimili wa polar.
Dhana muhimu
- Mfumo wa kuratibu polar hutoa njia mbadala ya kupata pointi katika ndege.
- Badilisha pointi kati ya kuratibu mstatili na polar kwa kutumia formula
\[x=r\cos θ \text{ and } y=r\sin θ \nonumber \]
na
\[r=\sqrt{x^2+y^2} \text{ and} \tan θ=\dfrac{y}{x}. \nonumber \]
- Ili mchoro wa polar kutoka kwa kazi ya polar iliyotolewa, fanya meza ya maadili na kuchukua faida ya mali ya mara kwa mara.
- Tumia fomu za uongofu ili kubadilisha equations kati ya kuratibu mstatili na polar.
- Kutambua ulinganifu katika curves polar, ambayo inaweza kutokea kwa njia ya pole, mhimili usawa, au mhimili wima.
faharasa
- kuratibu angular
- \(θ\)angle iliyoundwa na sehemu ya mstari inayounganisha asili kwa uhakika katika mfumo wa kuratibu wa polar na mhimili mzuri wa radial (x), kipimo kinyume
- cardioid
- curve ya ndege iliyofuatiliwa na hatua juu ya mzunguko wa mduara unaozunguka mzunguko uliowekwa wa radius sawa; equation ya cardioid ni\(r=a(1+\sin θ)\) au\(r=a(1+\cos θ)\)
- limaçon
- grafu ya equation\(r=a+b\sin θ\) au\(r=a+b\cos θ.\) Kama\(a=b\) basi grafu ni cardioid
- mhimili wa polar
- mhimili usawa katika mfumo wa kuratibu polar sambamba na\(r≥0\)
- polar kuratibu mfumo
- mfumo wa kupata pointi katika ndege. Kuratibu ni\(r\), kuratibu radial, na\(θ\), kuratibu angular
- mlinganyo wa polar
- equation au kazi inayohusiana na kuratibu radial kwa kuratibu angular katika mfumo wa kuratibu polar
- pole
- hatua ya kati ya mfumo wa kuratibu polar, sawa na asili ya mfumo wa Cartesian
- kuratibu radial
- \(r\)kuratibu katika mfumo wa kuratibu wa polar ambao hupima umbali kutoka kwa uhakika katika ndege hadi pole
- rose
- grafu ya equation polar\(r=a\cos 2θ\) au\(r=a\sin 2θ\) kwa mara kwa mara chanya\(a\)
- nafasi ya kujaza Curve
- Curve ambayo inachukuwa kabisa subset mbili-dimensional ya ndege halisi


