11.2: Calculus ya Curves Parametric
- Page ID
- 178385
- Kuamua derivatives na usawa wa tangents kwa curves parametric.
- Pata eneo chini ya safu ya parametric.
- Tumia equation kwa urefu wa safu ya safu ya parametric.
- Tumia fomu ya eneo la uso kwa kiasi kilichozalishwa na safu ya parametric.
Sasa kwa kuwa tumeanzisha dhana ya safu ya parameterized, hatua yetu inayofuata ni kujifunza jinsi ya kufanya kazi na dhana hii katika mazingira ya calculus. Kwa mfano, ikiwa tunajua parameterization ya curve iliyotolewa, inawezekana kuhesabu mteremko wa mstari wa tangent kwenye pembe? Vipi kuhusu urefu wa arc wa curve? Au eneo chini ya Curve?
Hali nyingine: Tuseme tungependa kuwakilisha eneo la baseball baada ya mpira majani mkono mtungi wa. Kama nafasi ya baseball inawakilishwa na Curve ndege\((x(t),y(t))\) basi tunapaswa kuwa na uwezo wa kutumia calculus kupata kasi ya mpira wakati wowote. Zaidi ya hayo, tunapaswa kuwa na uwezo wa mahesabu tu jinsi mbali kwamba mpira ina alisafiri kama kazi ya muda.
Derivatives ya Equations Paramet
Tunaanza kwa kuuliza jinsi ya kuhesabu mteremko wa mstari wa mstari kwenye safu ya parametric kwa uhakika. Fikiria Curve ya ndege inayofafanuliwa na equations parametric
\[\begin{align} x(t) &=2t+3 \label{eq1} \\ y(t) &=3t−4 \label{eq2} \end{align} \]
ndani\(−2≤t≤3\).
Grafu ya curve hii inaonekana kwenye Kielelezo\(\PageIndex{1}\). Ni sehemu ya mstari kuanzia saa\((−1,−10)\) na kuishia saa\((9,5).\)
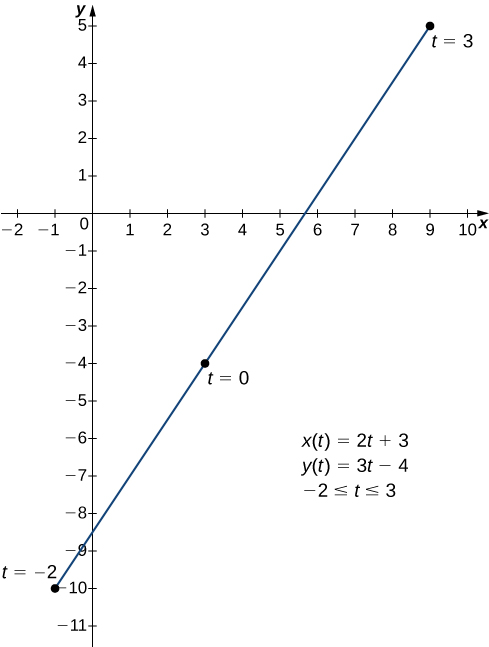
Tunaweza kuondoa parameter kwa kwanza kutatua Equation\ ref {eq1} kwa\(t\):
\(x(t)=2t+3\)
\(x−3=2t\)
\(t=\dfrac{x−3}{2}\).
Kubadilisha hii katika\(y(t)\) (Equation\ ref {eq2}), tunapata
\(y(t)=3t−4\)
\(y=3\left(\dfrac{x−3}{2}\right)−4\)
\(y=\dfrac{3x}{2}−\dfrac{9}{2}−4\)
\(y=\dfrac{3x}{2}−\dfrac{17}{2}\).
Mteremko wa mstari huu hutolewa na\(\dfrac{dy}{dx}=\dfrac{3}{2}\). Halafu tunahesabu\(x′(t)\) na\(y′(t)\). Hii inatoa\(x′(t)=2\) na\(y′(t)=3\). Taarifa kwamba
\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{3}{2}. \nonumber \]
Hii sio bahati mbaya, kama ilivyoelezwa katika theorem ifuatayo.
Fikiria Curve ndege inavyoelezwa na milinganyo parametric\(x=x(t)\) na\(y=y(t)\). Tuseme kwamba\(x′(t)\) na\(y′(t)\) kuwepo, na kudhani kwamba\(x′(t)≠0\). Kisha derivative\(\dfrac{dy}{dx}\) hutolewa na
\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{y′(t)}{x′(t)}. \label{paraD} \]
Theorem hii inaweza kuthibitishwa kwa kutumia Utawala wa Chain. Hasa, kudhani kwamba parameter\(t\) inaweza kuondolewa, kutoa kazi tofauti\(y=F(x)\). Kisha\(y(t)=F(x(t)).\) kutofautisha pande zote mbili za equation hii kwa kutumia Chain Utawala mavuno
\[y′(t)=F′\big(x(t)\big)x′(t), \nonumber \]
kwa hivyo
\[F′\big(x(t)\big)=\dfrac{y′(t)}{x′(t)}. \nonumber \]
Lakini\(F′\big(x(t)\big)=\dfrac{dy}{dx}\), ambayo inathibitisha theorem.
□
Equation\ ref {ParaD} inaweza kutumika kuhesabu derivatives ya curves ndege, pamoja na pointi muhimu. Kumbuka kwamba hatua muhimu ya kazi tofauti\(y=f(x)\) ni hatua yoyote\(x=x_0\) kama hiyo ama\(f′(x_0)=0\) au\(f′(x_0)\) haipo. Equation\ ref {ParaD} anatoa formula kwa mteremko wa mstari tangent kwa Curve defined parametrically bila kujali kama Curve inaweza kuwa ilivyoelezwa na kazi\(y=f(x)\) au la.
Mahesabu derivative\(\dfrac{dy}{dx}\) kwa kila moja ya yafuatayo parametrically defined curves ndege, na Machapisho pointi yoyote muhimu kwenye grafu zao.
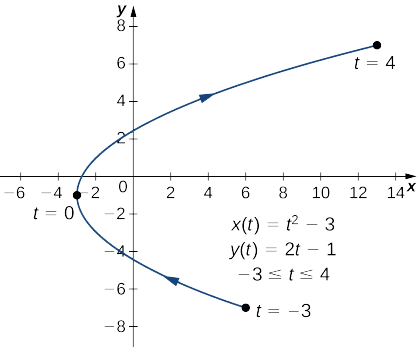
- \(x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4\)
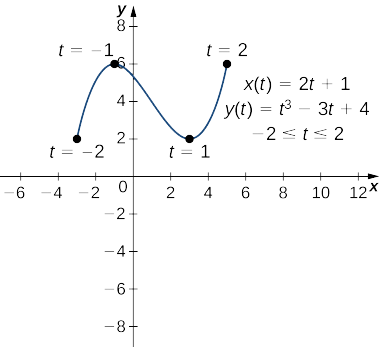
- \(x(t)=2t+1, \quad y(t)=t^3−3t+4, \quad\text{for }−2≤t≤2\)
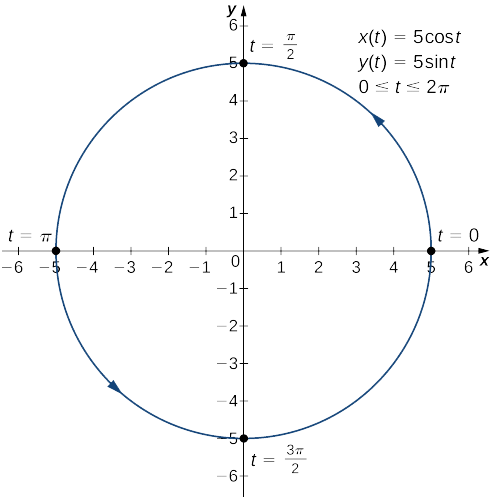
- \(x(t)=5\cos t, \quad y(t)=5\sin t, \quad\text{for }0≤t≤2π\)
Suluhisho
a. kuomba Equation\ ref {ParaD}, kwanza hesabu\(x′(t)\) na\(y′(t)\):
\(x′(t)=2t\)
\(y′(t)=2\).
Next mbadala hizi katika equation:
\(\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}\)
\(\dfrac{dy}{dx}=\dfrac{2}{2t}\)
\(\dfrac{dy}{dx}=\dfrac{1}{t}\).
derivative hii haijulikani wakati\(t=0\). Kuhesabu\(x(0)\) na\(y(0)\) kutoa\(x(0)=(0)^2−3=−3\) na\(y(0)=2(0)−1=−1\), ambayo inalingana na uhakika\((−3,−1)\) kwenye grafu. Grafu ya pembe hii ni ufunguzi wa parabola upande wa kulia, na uhakika\((−3,−1)\) ni kipeo chake kama inavyoonekana.
b Ili kuomba Equation\ ref {ParaD}, kwanza hesabu\(x′(t)\) na\(y′(t)\):
\(x′(t)=2\)
\(y′(t)=3t^2−3\).
Next mbadala hizi katika equation:
\(\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}\)
\(\dfrac{dy}{dx}=\dfrac{3t^2−3}{2}\).
Hii derivative ni sifuri wakati\(t=±1\). Wakati\(t=−1\) tuna
\(x(−1)=2(−1)+1=−1\)na\(y(−1)=(−1)^3−3(−1)+4=−1+3+4=6\),
ambayo inalingana na uhakika\((−1,6)\) kwenye grafu. Wakati\(t=1\) tuna
\(x(1)=2(1)+1=3\)na\(y(1)=(1)^3−3(1)+4=1−3+4=2,\)
ambayo inalingana na uhakika\((3,2)\) kwenye grafu. Hatua\((3,2)\) ni kiwango cha chini cha jamaa na uhakika\((−1,6)\) ni upeo wa jamaa, kama inavyoonekana katika grafu ifuatayo.
c Ili kuomba Equation\ ref {ParaD}, kwanza hesabu\(x′(t)\) na\(y′(t)\):
\(x′(t)=−5\sin t\)
\(y′(t)=5\cos t.\)
Next mbadala hizi katika equation:
\(\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}\)
\(\dfrac{dy}{dx}=\dfrac{5\cos t}{−5\sin t}\)
\(\dfrac{dy}{dx}=−\cot t.\)
derivative Hii ni sifuri wakati\(\cos t=0\) na\(\sin t=0.\) haijulikani wakati Hii inatoa\(t=0,\dfrac{π}{2},π,\dfrac{3π}{2},\) na pointi\(2π\) kama muhimu kwa t. Kubadilisha kila moja ya hizi katika\(x(t)\) na\(y(t)\), tunapata
| \(t\) | \(x(t)\) | \(y(t)\) |
|---|---|---|
| \ (t\)” style="wima align:katikati; "> 0 | \ (x (t)\)” style="wima align:katikati; "> 5 | \ (y (t)\)” style="wima align:katikati; "> 0 |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{π}{2}\) | \ (x (t)\)” style="wima align:katikati; "> 0 | \ (y (t)\)” style="wima align:katikati; "> 5 |
| \ (t\)” style="wima align:katikati; ">\(π\) | \ (x (t)\)” style="wima align:katikati; "> -5 | \ (y (t)\)” style="wima align:katikati; "> 0 |
| \ (t\)” style="wima align:katikati; ">\(\dfrac{3π}{2}\) | \ (x (t)\)” style="wima align:katikati; "> 0 | \ (y (t)\)” style="wima align:katikati; "> -5 |
| \ (t\)” style="wima align:katikati; ">\(2π\) | \ (x (t)\)” style="wima align:katikati; "> 5 | \ (y (t)\)” style="wima align:katikati; "> 0 |
Vipengele hivi vinahusiana na pande, juu, na chini ya mduara unaowakilishwa na usawa wa parametric (Kielelezo\(\PageIndex{4}\)). Kwenye upande wa kushoto na wa kulia wa mduara, derivative haijulikani, na juu na chini, derivative ni sawa na sifuri.
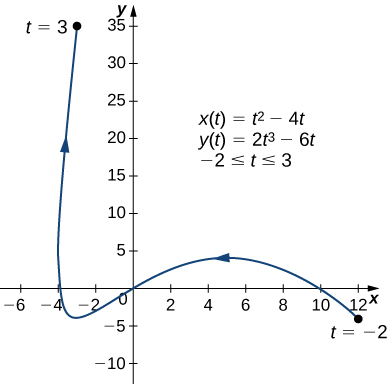
Tumia derivative\(dy/dx\) kwa Curve ya ndege iliyoelezwa na equations
\[x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤3 \nonumber \]
na Machapisho pointi yoyote muhimu kwenye grafu yake.
- Kidokezo
-
Tumia hesabu\(x′(t)\)\(y′(t)\) na utumie Equation\ ref {ParaD}.
- Jibu
-
\(x′(t)=2t−4\)na\(y′(t)=6t^2−6\), hivyo\(\dfrac{dy}{dx}=\dfrac{6t^2−6}{2t−4}=\dfrac{3t^2−3}{t−2}\).
Maneno haya haijulikani wakati\(t=2\) na sawa na sifuri wakati\(t=±1\).
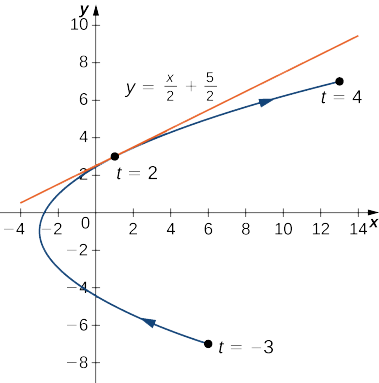
Find equation ya mstari tangent kwa Curve defined na equations
\[x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4 \nonumber \]
lini\(t=2\).
Suluhisho
Kwanza tafuta mteremko wa mstari wa tangent ukitumia Equation\ ref {ParaD}, ambayo ina maana ya kuhesabu\(x′(t)\) na\(y′(t)\):
\(x′(t)=2t\)
\(y′(t)=2\).
Next mbadala hizi katika equation:
\(\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}\)
\(\dfrac{dy}{dx}=\dfrac{2}{2t}\)
\(\dfrac{dy}{dx}=\dfrac{1}{t}\).
Wakati\(t=2, \dfrac{dy}{dx}=\dfrac{1}{2}\), hivyo hii ni mteremko wa mstari wa tangent. Kuhesabu\(x(2)\) na\(y(2)\) kutoa
\(x(2)=(2)^2−3=1\)na\(y(2)=2(2)−1=3\),
ambayo inalingana na uhakika\((1,3)\) kwenye grafu (Kielelezo\(\PageIndex{5}\)). Sasa tumia fomu ya mteremko wa equation ya mstari ili kupata equation ya mstari wa tangent:
\(y−y_0=m(x−x_0)\)
\(y−3=\dfrac{1}{2}(x−1)\)
\(y−3=\dfrac{1}{2}x−\dfrac{1}{2}\)
\(y=\dfrac{1}{2}x+\dfrac{5}{2}\).
Find equation ya mstari tangent kwa Curve defined na equations
\(x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤6\)lini\(t=5\).
- Kidokezo
-
Tumia hesabu\(x′(t)\)\(y′(t)\) na utumie Equation\ ref {ParaD}.
- Jibu
-
Equation ya mstari wa tangent ni\(y=24x+100.\)
Pili ili derivatives
Lengo letu la pili ni kuona jinsi ya kuchukua derivative pili ya kazi defined parametrically. Derivative ya pili ya kazi\(y=f(x)\) inaelezwa kuwa derivative ya derivative kwanza; yaani,
\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx}\left[\dfrac{dy}{dx}\right]. \label{eqD2} \]
Tangu
\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}, \nonumber \]
tunaweza kuchukua nafasi ya\(y\) pande zote mbili za Equation\ ref {eQD2} kwa\(\dfrac{dy}{dx}\). Hii inatupa
\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx} \left(\dfrac{dy}{dx} \right)=\dfrac{(d/dt)(dy/dx)}{dx/dt}.\label{paraD2} \]
Kama tunajua\(dy/dx\) kama kazi ya\(t\), basi formula hii ni moja kwa moja kuomba
Tumia derivative ya pili\(d^2y/dx^2\) kwa safu ya ndege iliyoelezwa na equations ya parametric\(x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4.\)
Suluhisho
Kutoka Mfano\(\PageIndex{1}\) tunajua kwamba\(\dfrac{dy}{dx}=\dfrac{2}{2t}=\dfrac{1}{t}\). Kutumia Equation\ ref {Parad2}, tunapata
\(\dfrac{d^2y}{dx^2}=\dfrac{(d/dt)(dy/dx)}{dx/dt}=\dfrac{(d/dt)(1/t)}{2t}=\dfrac{−t^{−2}}{2t}=−\dfrac{1}{2t^3}\).
Tumia derivative ya pili\(d^2y/dx^2\) kwa safu ya ndege inayoelezwa na equations
\(x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤3\)
na Machapisho pointi yoyote muhimu kwenye grafu yake.
- Kidokezo
-
Anza na suluhisho kutoka kwa zoezi la awali, na utumie Equation\ ref {Parad2}.
- Jibu
-
\(\dfrac{d^2y}{dx^2}=\dfrac{3t^2−12t+3}{2(t−2)^3}\). pointi muhimu\((5,4),\, (−3,−4)\), na\((−4,6).\)
Integrals Kuhusisha milinganyo Parametric
Sasa kwa kuwa tumeona jinsi ya kuhesabu derivative ya Curve ndege, swali la pili ni hili: Je, sisi kupata eneo chini ya Curve defined parametrically? Kumbuka cycloid inavyoelezwa na equations hizi parametric
\[ \begin{align*} x(t) &=t−\sin t \\[4pt] y(t) &=1−\cos t. \end{align*}\]
Tuseme tunataka kupata eneo la eneo la kivuli katika grafu ifuatayo.
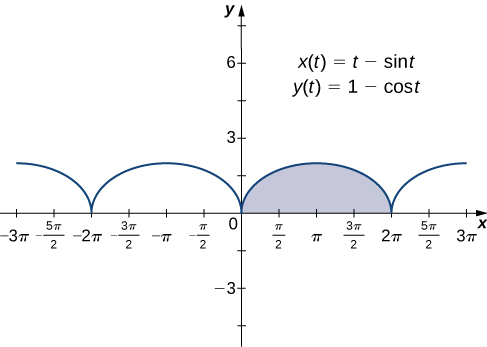
Kupata formula kwa eneo chini ya Curve defined na kazi
\[\begin{align*} x &=x(t) \\[4pt] y &=y(t) \end{align*}\]
wapi\(a≤t≤b\).
Tunadhani kuwa\(x(t)\) ni tofauti na kuanza na ugawaji sawa wa muda\(a≤t≤b\). Tuseme\(t_0=a<t_1<t_2<⋯<t_n=b\) na fikiria grafu ifuatayo.
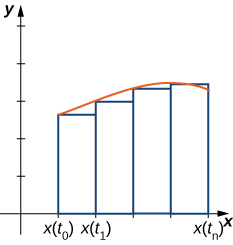
Tunatumia rectangles ili takriban eneo chini ya pembe. Urefu wa mstatili wa kawaida katika parametrization hii ni\(y(x(\bar{t_i}))\) kwa thamani fulani\(\bar{t_i}\) katika\(i^\text{th}\) subinterval, na upana unaweza kuhesabiwa kama\(x(t_i)−x(t_{i−1})\). Hivyo eneo la\(i^\text{th}\) mstatili linatolewa na
\[A_i=y(x(\bar{t_i}))(x(t_i)−x(t_{i−1})). \nonumber \]
Kisha Riemann jumla kwa ajili ya eneo ni
\[A_n=\sum_{i=1}^ny(x(\bar{t_i}))(x(t_i)−x(t_{i−1})).\nonumber \]
Kuzidisha na kugawa kila eneo kwa\(t_i−t_{i−1}\) anatoa
\[ \begin{align*} A_n &=\sum_{i=1}^ny(x(\bar{t_i})) \left(\dfrac{x(t_i)−x(t_{i−1})}{t_i−t_{i−1}}\right)(t_i−t_{i−1}) \\[4pt] &=\sum_{i=1}^ny(x(\bar{t_i})) \left(\dfrac{x(t_i)−x(t_{i−1})}{Δt}\right)Δt. \end{align*} \nonumber \]
Kuchukua kikomo kama\(n\) mbinu infinity inatoa
\[A=\lim_{n→∞}A_n=∫^b_ay(t)x′(t)\,dt. \nonumber \]
Hii inasababisha theorem ifuatayo.
Fikiria safu ya ndege isiyo ya kujitegemea inayoelezwa na milinganyo ya parametric
\[x=x(t),\quad y=y(t),\quad \text{for }a≤t≤b \nonumber \]
na kudhani kwamba\(x(t)\) ni differentiable. Eneo chini ya curve hii linatolewa na
\[A=∫^b_ay(t)x′(t)\,dt.\label{ParaArea} \]
Find eneo chini ya Curve ya cycloid defined na equations
\[x(t)=t−\sin t, \quad y(t)=1−\cos t, \quad \text{for }0≤t≤2π. \nonumber \]
Suluhisho
Kutumia Equation\ ref {ParaArea}, tuna
\ [kuanza {align*} A &=^b_ay (t) x′ (t)\, dt\\ [4pt]
&=^ {2π} _0 (1-\ cos t) (1-\ cos t)\, dt\\ [4pt]
&=^ {2π} _0 (1,1-2\ cos t+\ cos ^ 2t)\, dt\\\ [4pt]
&=^ {2π} _0\ kushoto (1,1-2\ cos t+\ dfrac {1+\ cos (2t)} {2}\ haki)\, dt\\ [4pt]
&=^ {2π} _0\ kushoto (\ dfrac {3} {2} -1\ cos t+ \ dfrac {\ cos (2t)} {2}\ haki)\, dt\\ [4pt]
&=\ dfrac {3t} {2} -2\ dhambi t+\ dfrac {\ dhambi (2t)} {4} ^ {2π}} _0\\ [4pt]
&=3π\ mwisho {align*}\]
Pata eneo chini ya pembe ya hypocycloid iliyoelezwa na equations
\[x(t)=3\cos t+\cos(3t), \quad y(t)=3\sin t−\sin(3t), \quad \text{for }0≤t≤π. \nonumber \]
- Kidokezo
-
Tumia Equation\ ref {ParaArea}, pamoja na utambulisho\(\sin α\sin β=\dfrac{1}{2}[\cos(α−β)−\cos(α+β)]\) na\(\sin^2t=\dfrac{1−\cos (2t)}{2}\).
- Jibu
-
\(A=3π\)(Kumbuka kwamba formula muhimu kwa kweli hutoa jibu hasi. Hii ni kutokana na ukweli kwamba\(x(t)\) ni kazi ya kupungua kwa muda,\([0,π];\) yaani, curve inafuatiliwa kutoka kulia kwenda kushoto.)
Urefu wa safu ya Curve ya Parametric
Mbali na kutafuta eneo chini ya safu ya parametric, wakati mwingine tunahitaji kupata urefu wa arc wa curve parametric. Katika kesi ya sehemu ya mstari, urefu wa arc ni sawa na umbali kati ya mwisho. Ikiwa chembe husafiri kutoka hatua\(A\) hadi kumweka\(B\) kando ya pembe, basi umbali ambao chembe husafiri ni urefu wa arc. Kuendeleza formula kwa urefu wa arc, tunaanza na makadirio na makundi ya mstari kama inavyoonekana kwenye grafu ifuatayo.
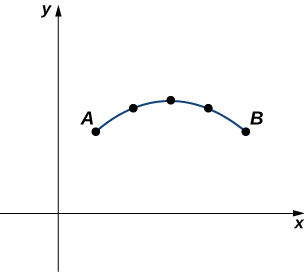
Kutokana na Curve ya ndege inayoelezwa na kazi\(x=x(t),\quad y=y(t),\quad \text{for }a≤t≤b\), tunaanza kwa kugawanya muda\([a,b]\) katika sehemu ndogo\(n\) sawa:\(t_0=a<t_1<t_2<⋯<t_n=b\). Upana wa kila subinterval hutolewa na\(Δt=(b−a)/n\). Tunaweza kuhesabu urefu wa kila sehemu ya mstari:
\[d_1=\sqrt{(x(t_1)−x(t_0))^2+(y(t_1)−y(t_0))^2} \nonumber \]
\[d_2=\sqrt{(x(t_2)−x(t_1))^2+(y(t_2)−y(t_1))^2} \nonumber \]
na kadhalika.
Kisha kuongeza haya juu. Tunaruhusu\(s\) kutaja urefu halisi wa arc na\(s_n\) kuashiria makadirio na makundi ya\(n\) mstari:
\[s≈\sum_{k=1}^ns_k=\sum_{k=1}^n\sqrt{(x(t_k)−x(t_{k−1}))^2+(y(t_k)−y(t_{k−1}))^2}. \label{arc5} \]
Ikiwa tunadhani kuwa\(x(t)\) na\(y(t)\) ni kazi tofauti za\(t\), basi Theorem ya Theorem ya Maana inatumika, hivyo katika kila subinterval\([t_{k−1},t_k]\) kuna kuwepo\(\hat{t_k}\) na\(\tilde{t_k}\) vile
\[x(t_k)−x(t_{k−1})=x′(\hat{t_k})(t_k−t_{k−1})=x′(\hat{t_k})\,Δt \nonumber \]
\[y(t_k)−y(t_{k−1})=y′(\tilde{t_k})(t_k−t_{k−1})=y′(\tilde{t_k})\,Δt. \nonumber \]
Kwa hiyo Equation\ ref {arc5} inakuwa
\ [kuanza {align*} s ≈\ sum_ {k=1} ^ns_k &=\ sum_ {k=1} ^n\ sqrt {(x′ (\ kofia {t_k}) Δt) ^2+ (y (\ tilde {t_k}) Δt) ^2}\\ [4pt]
&=\ sum_ {k = 1} ^n\ sqrt {(x′ (\ kofia {t_k}) ^2 (Δt) ^2+ (y(\ tilde {t_k}) ^2 (Δt) ^2}\\ [4pt]
&=\ sum_ {k=1} ^n\ sqrt {(x′ (\ kofia {t_k}) ^2+ (y (\ tilde {t_k}) ^2} Δt. \ mwisho {align*}\]
Hii ni jumla ya Riemann ambayo inakaribia urefu wa arc juu ya ugawaji wa muda\([a,b]\). Kama sisi zaidi kudhani kwamba derivatives ni kuendelea na kuruhusu idadi ya pointi katika kizigeu kuongezeka bila amefungwa, makadirio inakaribia halisi safu urefu. Hii inatoa
\ [kuanza {align*} s &=\ lim_ {n → Δ}\ sum_ {k=1} ^ns_k\\ [4pt]
&=\ lim_ {n → Δ}\ sum_ {k=1} ^n\ sqrt {(x (\ kofia {t_k}) ^2} Δt\\ [4pt]
&=^b_a\ sqrt {(x′ (t)) ^2+ (y( t)) ^2}\, dt. \ mwisho {align*}\]
Wakati wa kuchukua kikomo, maadili ya\(\hat{t_k}\) na yote\(\tilde{t_k}\) yaliyomo ndani ya muda huo wa kushuka kwa upana\(Δt\), hivyo wanapaswa kugeuza kwa thamani sawa.
Tunaweza muhtasari njia hii katika theorem ifuatayo.
Fikiria Curve ya ndege inayofafanuliwa na equations parametric
\[x=x(t), \quad y=y(t), \quad \text{for }t_1≤t≤t_2 \nonumber \]
na kudhani kwamba\(x(t)\) na\(y(t)\) ni differentiable kazi ya\(t\). Kisha urefu wa arc wa curve hii hutolewa na
\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt. \label{arcP} \]
Kwa hatua hii, derivation ya upande inaongoza kwa formula ya awali ya urefu wa arc. Hasa, tuseme parameter inaweza kuondolewa, na kusababisha kazi\(y=F(x)\). Kisha\(y(t)=F(x(t))\) na Utawala Chain anatoa
\[y′(t)=F′\big(x(t)\big)x′(t). \nonumber \]
Kubadilisha hii katika Equation\ ref {ArcP} anatoa
\ [kuanza {align*} s &=^ {t_2} _ {t_1}\ sqrt {\ kushoto (\ dfrac {dx} {dt}\ haki) ^2+\ kushoto (F( x)\ dfrac {dx} {dt}\ haki) ^2}\, dt\\ [4pt]
&=^ {t_2} _ {t_2} _ {dt}\ _1}\ sqrt {\ kushoto (\ dfrac {dx} {dt}\ kulia) ^2 (1+\ kushoto (F( x)\ haki) ^2)}\, dt\\ [4pt]
&=^ {t_2} _ {t_1} x (t)\ sqrt {1+\ kushoto (\ dfrac {dfrac} {dx} {dx\} haki) ^2}\, dt. \ mwisho {align*}\]
Hapa tuna kudhani kwamba\(x′(t)>0\), ambayo ni dhana nzuri. Utawala wa Chain hutoa\(dx=x′(t)\,dt,\) na kuruhusu\(a=x(t_1)\) na\(b=x(t_2)\) tunapata formula
\[s=∫^b_a\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}\,dx, \nonumber \]
ambayo ni formula ya urefu wa arc iliyopatikana katika Utangulizi wa Maombi ya Ushirikiano.
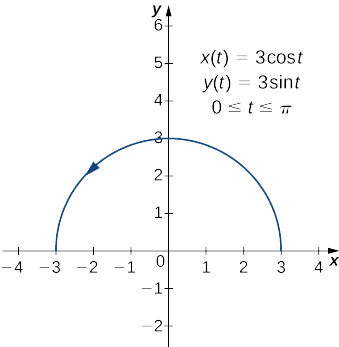
Pata urefu wa arc wa semicircle iliyoelezwa na equations
\[x(t)=3\cos t, \quad y(t)=3\sin t, \quad \text{for }0≤t≤π. \nonumber \]
Suluhisho
maadili ya\(t=0\)\(t=π\) kufuatilia nje Curve bluu katika Kielelezo\(\PageIndex{8}\). Kuamua urefu wake, tumia Equation\ ref {ArcP}:
\ [kuanza {align*} s &=\ int^ {t_2} _ {t_1}\ sqrt {\ kushoto (\ dfrac {dx} {dt}\ haki) ^2+\ kushoto (\ dfrac {dt} {dt}\ haki) ^2}\ [4pt]
&=^π_0\ sqrt {(—3\ dhambi t) ^2+ (3\ cos t) ^2}\, dt\\ [4pt]
&=^π_0\ sqrt {9\ dhambi ^ 2t+9\ cos^2t}\, dt\\ [4pt]
&=^π_0\ sqrt {9 (\ dhambi ^ 2t+\ cos ^ 2t)}\, dt\\ [4pt]
&=^π_03\, dt=3t\ kubwa|^π_0\\ [4pt]
&=3π\ maandishi {vitengo}. \ mwisho {align*}\]
Kumbuka kwamba formula ya urefu wa arc ya semicircle ni\(πr\) na radius ya mduara huu ni\(3\). Huu ni mfano mzuri wa kutumia calculus kupata formula inayojulikana ya wingi wa kijiometri.
Find urefu wa safu ya Curve defined na equations
\[x(t)=3t^2, \quad y(t)=2t^3, \quad \text{for }1≤t≤3. \nonumber \]
- Kidokezo
-
Tumia Equation\ ref {ArcP}.
- Jibu
-
\(s=2(10^{3/2}−2^{3/2})≈57.589\)vitengo
Sasa tunarudi tatizo lililofanywa mwanzoni mwa sehemu kuhusu baseball na kuacha mkono wa mtungi. Kupuuza athari za upinzani wa hewa (isipokuwa ni mpira wa pembe!) , mpira husafiri njia ya parabolic. Kutokana mkono mtungi ni katika asili na mpira husafiri kushoto kwenda kulia katika mwelekeo wa chanya\(x\) -axis, milinganyo parametric kwa Curve hii inaweza kuandikwa kama
\[x(t)=140t, \quad y(t)=−16t^2+2t \nonumber \]
ambapo\(t\) inawakilisha wakati. Sisi kwanza kuhesabu umbali mpira husafiri kama kazi ya muda. Umbali huu unawakilishwa na urefu wa arc. Tunaweza kurekebisha formula ya urefu wa arc kidogo. Kwanza kuandika upya kazi\(x(t)\) na\(y(t)\) kutumia v kama variable huru, ili kuondoa machafuko yoyote na parameter\(t\):
\[x(v)=140v, \quad y(v)=−16v^2+2v. \nonumber \]
Kisha tunaandika formula ya urefu wa arc kama ifuatavyo:
\ [kuanza {align*} s (t) &=^t_0\ sqrt {(\ dfrac {dx} {dv}) ^2+ (\ dfrac {dv} {dv}) ^2}\, dv\\ [4pt]
&=^t_0\ sqrt {140^2+ (-32v+2) ^2}\ dv\ mwisho {align*}\]
Variable\(v\) vitendo kama variable dummy kwamba kutoweka baada ya ushirikiano, na kuacha urefu wa arc kama kazi ya muda\(t\). Ili kuunganisha maneno haya tunaweza kutumia formula kutoka Kiambatisho A,
\[∫\sqrt{a^2+u^2}\,du=\dfrac{u}{2}\sqrt{a^2+u^2}+\dfrac{a^2}{2}\ln ∣u+\sqrt{a^2+u^2}∣+C. \nonumber \]
Sisi kuweka\(a=140\) na\(u=−32v+2.\) hii inatoa\(du=−32\,dv,\) hivyo\(dv=−\dfrac{1}{32}\,du.\) Kwa hiyo
\ [kuanza {align*}\ sqrt {140^2+ (-32v+2) ^2}\, dv &=\ dfrac {1} {32}\ sqrt {a^2+u ^ 2}\, du\\ [4pt]
&=\dfrac {1} {1} {32}\ kushoto [\ dfrac {(-32v+2)}} {2}\ sqrt {140^2+ (-32v+2) ^2} +\ dfrac {140^2} {2}\ ln (-32v+2) +\ sqrt {140^2+ (-32v+2) ^2} |+C\ haki]\ mwisho {align*}\]
na
\ [kuanza {align*} s (t) &=-\ dfrac {1} {32}\ kushoto [\ dfrac {(-32t+2)} {2}\ sqrt {140^2+ (-32t+2) ^2} +\ dfrac {140^2} {2}\ ln\ kushoto | (-32t+2) +\ sqrt {140^2+ (-32t+2) ^2}\ haki |\ haki] +\ dfrac {1} {32}\ kushoto [\ sqrt {140^2^2} +\ dfrac {140^2} {2}\ ln\ kushoto |2+\ sqrt {140^2^2}\ haki |\ haki]\\ [4pt]
&=\ kushoto (\ dfrac {t} {2} -\ dfrac {1} {32}\ haki)\ sqrt {1024t^2-128t+19604} -\ dfrac {1225} {4}\ ln\ kushoto | (-32t+2) +\ sqrt {1024t ^2-128t+19604}\ haki |+\ dfrac {\ sqrt {19604}} {32} +\ dfrac {1225} {4}\ ln (2+\ sqrt {19604})\ mwisho {align*}. \ nambari isiyo\]
Kazi hii inawakilisha umbali uliosafiri na mpira kama kazi ya muda. Ili kuhesabu kasi, chukua derivative ya kazi hii kwa heshima na\(t\). Ingawa hii inaweza kuonekana kama kazi ngumu, inawezekana kupata jibu moja kwa moja kutoka Theorem ya Msingi ya Calculus:
\[\dfrac{d}{dx}∫^x_af(u)\,du=f(x). \nonumber \]
Kwa hiyo
\ [kuanza {align*} s′ (t) &=\ dfrac {d} {dt}\ Big [s (t)\ Big]\\ [4pt]
&=\ dfrac {d} {dt}\ kushoto [^t_0\ sqrt {140^2+ (-32v+2) ^2}\\ haki]\\ [4pt]
&=\ sqrt {140^2+ (-32t+2) ^2}\\ [4pt]
&=\ sqrt {1024t^2,18t+19604}\\ [4pt]
&=2\ sqrt {256t^2,12t+4901}. \ mwisho {align*}\ nonumber\]
Theluthi moja ya pili baada ya mpira kuacha mkono wa mtungi, umbali unaosafiri ni sawa na
\ [kuanza {align*} s\ kushoto (\ frac {1} {3}\ kulia) &=\ kushoto (\ frac {1/3} {2}}}\ frac {1} {32}\ haki)\ sqrt {1024\ kushoto (\ frac {1} {1}\ haki) ^2—128\ kushoto (\ frac {1} {3}\ kulia) +19604}\\
&\\ FRAC {1225} {4}\ ln\ Bigg|\ kushoto (-32\ kushoto (\ frac {1} {3}\ haki) +2\ haki) +\ sqrt {1024\ kushoto (\ frac {1} {1} {1} {1}\ haki) ^2—128\ kushoto (\ frac {1} {3}\ haki) +19604}\ Bigg|\\
&+\ frac {\ sqrt {19604}} {32} +\ frac {1225} {4}\ ln (2+\ sqrt {19604})\\ [4pt]
&≈ 46.69\ maandishi {miguu}. \ mwisho {align*}\]
Thamani hii ni zaidi ya robo tatu ya njia ya sahani ya nyumbani. Kasi ya mpira ni
\(s′\left(\frac{1}{3}\right)=2\sqrt{256\left(\frac{1}{3}\right)^2−32\left(\frac{1}{3}\right)+4901}≈140.27\)ft/s.
Kasi hii inatafsiriwa kwa takriban\(95\) mph-fastball kuu ya ligi.
Eneo la uso lililozalishwa na Curve ya Parametric
Kumbuka tatizo la kutafuta eneo la uso wa kiasi cha mapinduzi. Katika Curve Urefu na uso Area, sisi inayotokana formula kwa ajili ya kutafuta eneo la uso wa kiasi yanayotokana na kazi\(y=f(x)\) kutoka\(x=a\) kwa\(x=b,\) revolved kuzunguka\(x\) -axis:
\[S=2π∫^b_af(x)\sqrt{1+(f′(x))^2}\,dx. \nonumber \]
Sasa tunaona kiasi cha mapinduzi yanayotokana na yanazunguka Curve parametrically defined\(x=x(t), \quad y=y(t), \quad \text{for }a≤t≤b\) kuzunguka\(x\) -axis kama inavyoonekana katika Kielelezo\(\PageIndex{9}\).
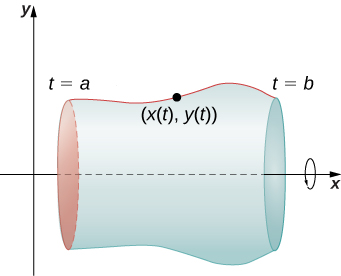
Fomu inayofanana kwa Curve iliyofafanuliwa kwa parametrically ni
\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt \label{ParSurface} \]
zinazotolewa kwamba\(y(t)\) si hasi juu ya\([a,b]\).
Pata eneo la uso wa eneo la radius\(r\) unaozingatia asili.
Suluhisho
Tunaanza na safu iliyofafanuliwa na equations
\[x(t)=r\cos t, \quad y(t)=r\sin t, \quad \text{for }0≤t≤π. \nonumber \]
Hii inazalisha semicircle juu ya radius\(r\) unaozingatia katika asili kama inavyoonekana katika grafu ifuatayo.
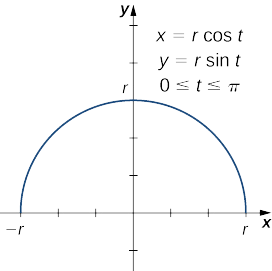
Wakati Curve hii inazunguka\(x\) -axis, inazalisha nyanja ya radius\(r\). Ili kuhesabu eneo la uso wa nyanja, tunatumia Equation\ ref {ParSurface}:
\ [kuanza {align*} S &= 2π^b_ay (t)\ sqrt {(x′ (t)) ^2+ (y (t)) ^2}\, dt\\ [4pt]
&=2π^π_0r\ dhambi t\ sqrt {(-r\ dhambi t) ^2+ (r\ cos t) ^2}\, dt\\\ [4pt]
&=2π^π_0r\ sin t\ sqrt {r ^ 2\ dhambi ^ 2t+r ^ 2\ cos^2t}\, dt\\ [4pt]
&=2π^π_0r\ dhambi t\ sqrt {r ^ 2 (\ dhambi ^ 2t+\ cos ^ 2t)}\, dt\\ [4pt]
&=2π^π_0r^2\ dhambi t\, dt\\ [4pt]
&=2πr^2\ kushoto (\ cos t\ kubwa|^π_0\ haki)\\ [4pt]
&=2πr^2 (∙\ cos π+\ cos 0)\\ [4pt]
&=4πr^2\ maandishi {vitengo} ^2. \ mwisho {align*}\ nonumber\]
Hii ni, kwa kweli, formula ya eneo la uso wa nyanja.
Find eneo la uso yanayotokana wakati Curve ndege inavyoelezwa na equations
\[x(t)=t^3, \quad y(t)=t^2, \quad \text{for }0≤t≤1 \nonumber \]
ni revolved kuzunguka\(x\) -axis.
- Kidokezo
-
Matumizi Equation\ ref {ParSurface}. Wakati wa kutathmini muhimu, tumia\(u\) -badala.
- Jibu
-
\(A=\dfrac{π(494\sqrt{13}+128)}{1215} \text{ units}^2\)
Dhana muhimu
- Derivative ya curve parametrically defined\(x=x(t)\) na\(y=y(t)\) inaweza kuhesabiwa kwa kutumia formula\(\dfrac{dy}{dx}=\dfrac{y′(t)}{x′(t)}\). Kutumia derivative, tunaweza kupata equation ya mstari tangent kwa curve parametric.
- Eneo kati ya safu ya parametric na\(x\) -axis inaweza kuamua kwa kutumia formula\(\displaystyle A=∫^{t_2}_{t_1}y(t)x′(t)\,dt.\)
- Urefu wa arc wa curve ya parametric unaweza kuhesabiwa kwa kutumia formula\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt. \nonumber \]
- Eneo la uso wa kiasi cha mapinduzi kilichozunguka\(x\) -axis hutolewa na\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt. \nonumber \]
- Ikiwa curve inazunguka\(y\) -axis, basi formula ni\[S=2π∫^b_a x(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt. \nonumber \]
Mlinganyo muhimu
- Derivative ya usawa wa parametric
\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{y′(t)}{x′(t)} \nonumber \]
- Derivative ya pili ya equations parametric
\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)=\dfrac{(d/dt)(dy/dx)}{dx/dt} \nonumber \]
- Eneo chini ya safu ya parametric
\[A=∫^b_ay(t)x′(t)\,dt \nonumber \]
- Urefu wa safu ya curve ya parametric
\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \nonumber \]
- Eneo la uso linalozalishwa na curve ya parametric
\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt \nonumber \]


