11.1: Ulinganifu wa parametric

Malengo ya kujifunza

• Plot Curve ilivyoelezwa na equations parametric.
• Badilisha equations parametric ya Curve katika fomu\(y=f(x)\).
• Tambua equations parametric ya curves msingi, kama vile mstari na mduara.
• Tambua equations parametric ya cycloid.

Katika sehemu hii tunachunguza equations parametric na grafu zao. Katika mfumo wa kuratibu mbili-dimensional, equations parametric ni muhimu kwa kuelezea curves ambayo si lazima kazi. Kipimo ni tofauti ya kujitegemea ambayo yote\(x\) na\(y\) hutegemea, na kama parameter inavyoongezeka, maadili ya\(x\) na\(y\) kufuatilia njia kwenye safu ya ndege. Kwa mfano, kama parameter ni\(t\) (uchaguzi wa kawaida), basi\(t\) inaweza kuwakilisha wakati. Kisha\(x\) na\(y\) hufafanuliwa kama kazi za muda, na\((x(t),y(t))\) inaweza kuelezea msimamo katika ndege ya kitu fulani kama hatua pamoja njia ikiwa.

Ulinganifu wa parametric na Grafu zao

Fikiria obiti ya Dunia karibu na Jua. Mwaka wetu unakaribia siku 365.25, lakini kwa majadiliano haya tutatumia siku 365. Mnamo Januari 1 ya kila mwaka, eneo la kimwili la Dunia kwa heshima na Jua ni karibu sawa, isipokuwa kwa miaka ya leap, wakati bakia iliyoletwa na\(\frac{1}{4}\) siku ya ziada ya muda wa mzunguko imejengwa kwenye kalenda. Tunaita Januari 1 “siku ya 1" ya mwaka. Kisha, kwa mfano, siku 31 ni Januari 31, siku 59 ni Februari 28, na kadhalika.

Idadi ya siku katika mwaka inaweza kuchukuliwa kuwa tofauti inayoamua msimamo wa Dunia katika obiti yake. Kama Dunia inavyozunguka Jua, eneo lake la kimwili linabadilika kuhusiana na Jua. Baada ya mwaka mmoja kamili, tunarudi ambapo tulianza, na mwaka mpya huanza. Kulingana na sheria za Kepler za mwendo wa sayari, umbo la obiti ni elliptical, huku Jua likiwa na lengo moja la duaradufu. Tunasoma wazo hili kwa undani zaidi katika Sehemu za Conic.

Kielelezo\(\PageIndex{1}\): Obiti ya Dunia karibu na Jua katika mwaka mmoja.

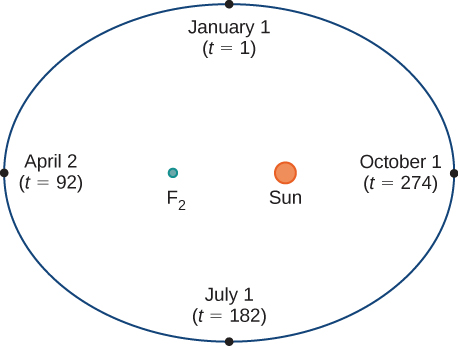
Kielelezo\( \PageIndex{1}\) inaonyesha obiti ya Dunia karibu na Jua wakati wa mwaka mmoja. Hatua iliyoandikwa\(F_2\) ni moja ya foci ya ellipse; lengo lingine linachukuliwa na Jua. Ikiwa tunaweka safu za kuratibu juu ya grafu hii, basi tunaweza kugawa jozi zilizoamriwa kwa kila hatua kwenye duaradufu (Kielelezo\( \PageIndex{2}\)). Kisha kila\(x\) thamani kwenye grafu ni thamani ya nafasi kama kazi ya muda, na kila\(y\) thamani pia ni thamani ya nafasi kama kazi ya muda. Kwa hiyo, kila hatua kwenye grafu inalingana na thamani ya nafasi ya Dunia kama kazi ya wakati.

Kielelezo\(\PageIndex{2}\): Kuratibu axes superimposed juu ya obiti ya Dunia.

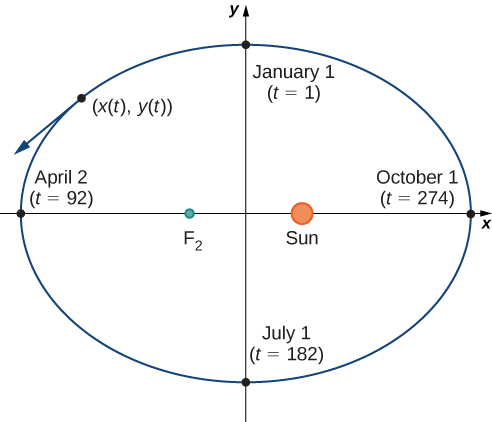
Tunaweza kuamua kazi kwa\(x(t)\) na\(y(t)\), na hivyo parameterizing obiti ya Dunia karibu na jua. Variable\(t\) inaitwa parameter ya kujitegemea na, katika muktadha huu, inawakilisha wakati kuhusiana na mwanzo wa kila mwaka.

Curve katika\((x,y)\) ndege inaweza kuwakilishwa parametrically. Equations ambayo hutumiwa kufafanua curve huitwa equations parametric.

Ufafanuzi: Ulinganifu wa parametric

Kama\(x\) na\(y\) ni kazi ya kuendelea ya\(t\) juu ya muda\(I\), basi equations

\[x=x(t) \nonumber \]

na

\[y=y(t) \nonumber \]

huitwa equations parametric na\(t\) inaitwa parameter. Seti ya pointi\((x,y)\) zilizopatikana kama\(t\) inatofautiana juu ya muda\(I\) huitwa grafu ya equations parametric. Grafu ya equations parametric inaitwa curve parametric au curve ndege, na inaashiria na\(C\).

Angalia katika ufafanuzi huu kwamba\(x\) na\(y\) hutumiwa kwa njia mbili. Ya kwanza ni kama kazi za kutofautiana kwa kujitegemea\(t\). Kama\(t\) inatofautiana juu ya muda\(I\), kazi\(x(t)\) na\(y(t)\) kuzalisha seti ya jozi zilizoamriwa\((x,y)\). Seti hii ya jozi zilizoamriwa huzalisha grafu ya equations parametric. Katika matumizi haya ya pili, kuteua jozi zilizoamriwa,\(x\) na\(y\) ni vigezo. Ni muhimu kutofautisha vigezo\(x\) na\(y\) kutoka kwa kazi\(x(t)\) na\(y(t)\).

Mfano\(\PageIndex{1}\): Graphing a Parametrically Defined Curve

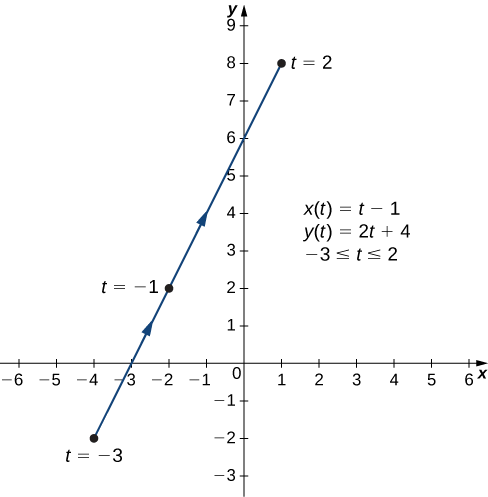
Mchoro curves ilivyoelezwa na equations zifuatazo parametric:

1. \(x(t)=t−1, \quad y(t)=2t+4,\quad \text{for }−3≤t≤2\)
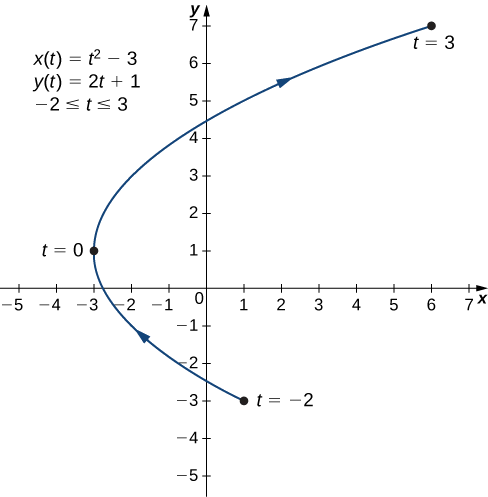
2. \(x(t)=t^2−3, \quad y(t)=2t+1,\quad \text{for }−2≤t≤3\)
3. \(x(t)=4 \cos t, \quad y(t)=4 \sin t,\quad \text{for }0≤t≤2π\)

Suluhisho

Ili kuunda grafu ya safu hii, kwanza weka meza ya maadili. Kwa kuwa variable huru katika wote\(x(t)\) na\(y(t)\) ni\(t\), hebu\(t\) kuonekana katika safu ya kwanza. Kisha\(x(t)\) na\(y(t)\) itaonekana kwenye nguzo ya pili na ya tatu ya meza.

\(t\)	\(x(t)\)	\(y(t)\)
\ (t\)” style="wima align:katikati; "> -1 3	\ (x (t)\)” style="wima align:katikati; ">-4	\ (y (t)\)” style="wima align:katikati; ">-1 2
\ (t\)” style="wima align:katikati; ">-1 2	\ (x (t)\)” style="wima align:katikati; ">-3	\ (y (t)\)” style="wima align:katikati; "> 0
\ (t\)” style="wima align:katikati; ">-1	\ (x (t)\)” style="wima align:katikati; ">-1 2	\ (y (t)\)” style="wima align:katikati; "> 2
\ (t\)” style="wima align:katikati; "> 0	\ (x (t)\)” style="wima align:katikati; ">-1	\ (y (t)\)” style="wima align:katikati; "> 4
\ (t\)” style="wima align:katikati; "> 1	\ (x (t)\)” style="wima align:katikati; "> 0	\ (y (t)\)” style="wima align:katikati; "> 6
\ (t\)” style="wima align:katikati; "> 2	\ (x (t)\)” style="wima align:katikati; "> 1	\ (y (t)\)” style="wima align:katikati; "> 8

Nguzo ya pili na ya tatu katika meza hii hutoa seti ya pointi zilizopangwa. Grafu ya pointi hizi inaonekana kwenye Kielelezo\( \PageIndex{3}\). Mishale kwenye grafu inaonyesha mwelekeo wa grafu, yaani, mwelekeo ambao hatua huenda kwenye grafu kama t inatofautiana kutoka -3 hadi 2.

Kielelezo\(\PageIndex{3}\): Grafu ya Curve ndege ilivyoelezwa na equations parametric katika sehemu a.

b Ili kuunda grafu ya safu hii, tena kuanzisha meza ya maadili.

\(t\)	\(x(t)\)	\(y(t)\)
\ (t\)” style="wima align:katikati; ">-1 2	\ (x (t)\)” style="wima align:katikati; "> 1	\ (y (t)\)” style="wima align:katikati; ">-3
\ (t\)” style="wima align:katikati; ">-1	\ (x (t)\)” style="wima align:katikati; ">-1 2	\ (y (t)\)” style="wima align:katikati; ">-1
\ (t\)” style="wima align:katikati; "> 0	\ (x (t)\)” style="wima align:katikati; ">-3	\ (y (t)\)” style="wima align:katikati; "> 1
\ (t\)” style="wima align:katikati; "> 1	\ (x (t)\)” style="wima align:katikati; ">-1 2	\ (y (t)\)” style="wima align:katikati; "> 3
\ (t\)” style="wima align:katikati; "> 2	\ (x (t)\)” style="wima align:katikati; "> 1	\ (y (t)\)” style="wima align:katikati; "> 5
\ (t\)” style="wima align:katikati; "> 3	\ (x (t)\)” style="wima align:katikati; "> 6	\ (y (t)\)” style="wima align:katikati; "> 7

Nguzo ya pili na ya tatu katika meza hii hutoa seti ya pointi zilizopangwa (Kielelezo\( \PageIndex{4}\)). Hatua ya kwanza kwenye grafu (sambamba na\(t=−2\)) ina kuratibu\((1,−3)\), na hatua ya mwisho (sambamba na\(t=3\)) ina kuratibu\((6,7)\). Kama\(t\) ikiendelea kutoka\(−2\) kwa\(3\), uhakika juu ya Curve husafiri pamoja parabola. Mwelekeo hatua hatua huitwa tena mwelekeo na unaonyeshwa kwenye grafu.

Kielelezo\(\PageIndex{4}\): Grafu ya Curve ya ndege iliyoelezwa na equations parametric katika sehemu b.

c Katika kesi hii, tumia wingi wa\(π/6\) kwa\(t\) na uunda meza nyingine ya maadili:

\(t\)	\(x(t)\)	\(y(t)\)	\(t\)	\(x(t)\)	\(y(t)\)
\ (t\)” style="wima align:katikati; "> 0	\ (x (t)\)” style="wima align:katikati; "> 4	\ (y (t)\)” style="wima align:katikati; "> 0	\ (t\)” style="wima align:katikati; ">\(\frac{7π}{6}\)	\ (x (t)\)” style="wima align:katikati; ">\(-2\sqrt{3}≈−3.5\)	\ (y (t)\)” style="wima align:katikati; ">-2
\ (t\)” style="wima align:katikati; ">\(\frac{π}{6}\)	\ (x (t)\)” style="wima align:katikati; ">\(2\sqrt{3}≈3.5\)	\ (y (t)\)” style="wima align:katikati; "> 2	\ (t\)” style="wima align:katikati; ">\(\frac{4π}{3}\)	\ (x (t)\)” style="wima align:middle; ">-1 2	\ (y (t)\)” style="wima align:katikati; ">\(−2\sqrt{3}≈−3.5\)
\ (t\)” style="wima align:katikati; ">\(\frac{π}{3}\)	\ (x (t)\)” style="wima align:katikati; "> 2	\ (y (t)\)” style="wima align:katikati; ">\(2\sqrt{3}≈3.5\)	\ (t\)” style="wima align:katikati; ">\(\frac{3π}{2}\)	\ (x (t)\)” style="wima align:katikati; "> 0	\ (y (t)\)” style="wima align:katikati; ">-4
\ (t\)” style="wima align:katikati; ">\(\frac{π}{2}\)	\ (x (t)\)” style="wima align:katikati; "> 0	\ (y (t)\)” style="wima align:katikati; "> 4	\ (t\)” style="wima align:katikati; ">\(\frac{5π}{3}\)	\ (x (t)\)” style="wima align:katikati; "> 2	\ (y (t)\)” style="wima align:katikati; ">\(−2\sqrt{3}≈−3.5\)
\ (t\)” style="wima align:katikati; ">\(\frac{2π}{3}\)	\ (x (t)\)” style="wima align:middle; ">-1 2	\ (y (t)\)” style="wima align:katikati; ">\(2\sqrt{3}≈3.5\)	\ (t\)” style="wima align:katikati; ">\(\frac{11π}{6}\)	\ (x (t)\)” style="wima align:katikati; ">\(2\sqrt{3}≈3.5\)	\ (y (t)\)” style="wima align:katikati; ">-2
\ (t\)” style="wima align:katikati; ">\(\frac{5π}{6}\)	\ (x (t)\)” style="wima align:katikati; ">\(−2\sqrt{3}≈−3.5\)	\ (y (t)\)” style="wima align:katikati; "> 2	\ (t\)” style="wima align:katikati; ">\(2π\)	\ (x (t)\)” style="wima align:katikati; "> 4	\ (y (t)\)” style="wima align:katikati; "> 0
\ (t\)” style="wima align:katikati; ">\(π\)	\ (x (t)\)” style="wima align:katikati; ">-4	\ (y (t)\)” style="wima align:katikati; "> 0	\ (t\)” style="wima align:katikati; ">	\ (x (t)\)” style="wima align:katikati; ">	\ (y (t)\)” style="wima align:katikati; ">

Grafu ya safu hii ya ndege inaonekana kwenye grafu ifuatayo.

Kielelezo\(\PageIndex{5}\): Grafu ya Curve ya ndege iliyoelezwa na equations parametric katika sehemu c.

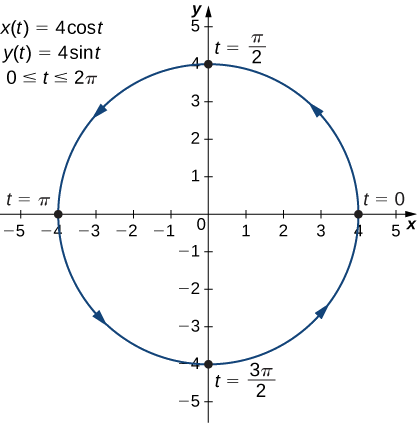
Hii ni grafu ya mduara na radius\(4\) iliyozingatia asili, na mwelekeo wa kinyume. Hatua ya mwanzo na pointi za mwisho za curve zote zina kuratibu\((4,0)\).

Zoezi\(\PageIndex{1}\)

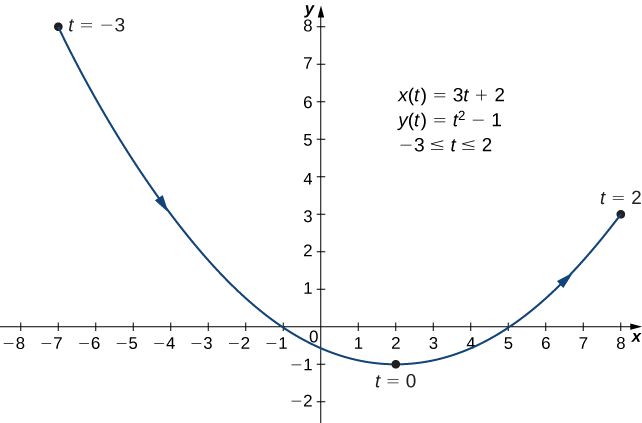
Mchoro curve ilivyoelezwa na equations parametric

\[ x(t)=3t+2,\quad y(t)=t^2−1,\quad \text{for }−3≤t≤2. \nonumber \]

Kidokezo

Fanya meza ya maadili\(x(t)\) na\(y(t)\) kutumia\(t\) maadili kutoka\(−3\) kwa\(2\).

Jibu

Kuondoa Parameter

Ili kuelewa vizuri grafu ya Curve kuwakilishwa parametrically, ni muhimu kuandika upya equations mbili kama equation moja zinazohusiana vigezo\(x\) na\(y\). Kisha tunaweza kutumia maarifa yoyote ya awali ya equations ya curves katika ndege kutambua Curve. Kwa mfano, equations kuelezea Curve ndege katika Mfano\(\PageIndex{1b}\) ni

\[\begin{align} x(t) &=t^2−3 \label{x1} \\[4pt] y(t) &=2t+1 \label{y1} \end{align} \]

juu ya kanda\(-2 \le t \le 3.\)

Kutatua Equation\ ref {y1} kwa\(t\) anatoa

\[t=\dfrac{y−1}{2}. \nonumber \]

Hii inaweza kubadilishwa katika Equation\ ref {x1}:

\[\begin{align} x &=\left(\dfrac{y−1}{2}\right)^2−3 \\[4pt] &=\dfrac{y^2−2y+1}{4}−3 \\[4pt] &=\dfrac{y^2−2y−11}{4}. \label{y2}\end{align} \]

Equation\ ref {y2} inaeleza\(x\) kama kazi ya\(y\). Hatua hizi hutoa mfano wa kuondoa parameter. Grafu ya kazi hii ni ufunguzi wa parabola kwa haki (Kielelezo\(\PageIndex{4}\)). Kumbuka kwamba Curve ndege ilianza saa\((1,−3)\) na kumalizika saa\((6,7)\). Vikwazo hivi vilikuwa kutokana na kizuizi kwenye parameter\(t\).

Mfano\(\PageIndex{2}\): Eliminating the Parameter

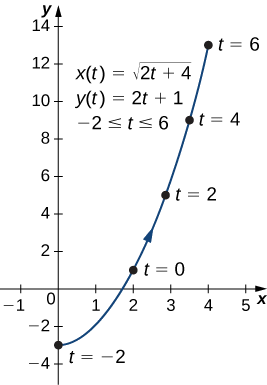
Ondoa parameter kwa kila moja ya ndege ya ndege iliyoelezwa na equations zifuatazo za parametric na kuelezea grafu inayosababisha.

1. \(x(t)=\sqrt{2t+4}, \quad y(t)=2t+1,\quad \text{for }−2≤t≤6\)
2. \(x(t)=4\cos t, \quad y(t)=3\sin t,\quad \text{for }0≤t≤2π\)

Suluhisho

Ili kuondoa parameter, tunaweza kutatua mojawapo ya equations kwa\(t\). Kwa mfano, kutatua equation kwanza kwa\(t\) anatoa

\[\begin{align*} x &=\sqrt{2t+4} \\[4pt] x^2 &=2t+4 \\[4pt] x^2−4 &=2t \\[4pt] t &=\dfrac{x^2−4}{2}. \end{align*}\]

Kumbuka kwamba wakati sisi mraba pande zote mbili ni muhimu kuchunguza hilo\(x≥0\). Kubadilisha\(t=\dfrac{x^2−4}{2}\) katika\(y(t)\) mavuno

\[ y(t)=2t+1 \nonumber \]

\[ y=2\left(\dfrac{x^2−4}{2}\right)+1 \nonumber \]

\[ y=x^2−4+1 \nonumber \]

\[ y=x^2−3. \nonumber \]

Hii ni equation ya parabola kufungua zaidi. Kuna, hata hivyo, kizuizi cha kikoa kwa sababu ya mipaka kwenye parameter\(t\). Wakati\(t=−2\),\(x=\sqrt{2(−2)+4}=0\), na wakati\(t=6\),\(x=\sqrt{2(6)+4}=4\). Grafu ya safu hii ya ndege ifuatavyo.

Kielelezo\(\PageIndex{6}\): Grafu ya Curve ndege ilivyoelezwa na equations parametric katika sehemu a.

b Wakati mwingine ni muhimu kuwa ubunifu kidogo katika kuondoa parameter. Ulinganisho wa parametric kwa mfano huu ni

\[ x(t)=4 \cos t\nonumber \]

na

\[ y(t)=3 \sin t\nonumber \]

Kutatua equation ama kwa\(t\) moja kwa moja si vyema kwa sababu sine na cosine si kazi moja kwa moja. Hata hivyo, kugawa equation kwanza\(4\) na na equation pili na\(3\) (na kukandamiza\(t\)) inatupa

\[ \cos t=\dfrac{x}{4}\nonumber \]

na

\[ \sin t=\dfrac{y}{3}.\nonumber \]

Sasa tumia utambulisho wa Pythagorean\(\cos^2t+\sin^2t=1\) na uweke nafasi ya maneno\(\sin t\)\(\cos t\) na kwa maneno sawa kulingana\(x\) na na\(y\). Hii inatoa

\[ \left(\dfrac{x}{4}\right)^2+\left(\dfrac{y}{3}\right)^2=1 \nonumber \]

\[ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1. \nonumber \]

Hii ni equation ya duaradufu usawa unaozingatia katika asili, na mhimili nusu kuu\(4\) na mhimili nusu madogo\(3\) kama inavyoonekana katika grafu ifuatayo.

Kielelezo\(\PageIndex{7}\): Grafu ya Curve ya ndege iliyoelezwa na equations parametric katika sehemu b.

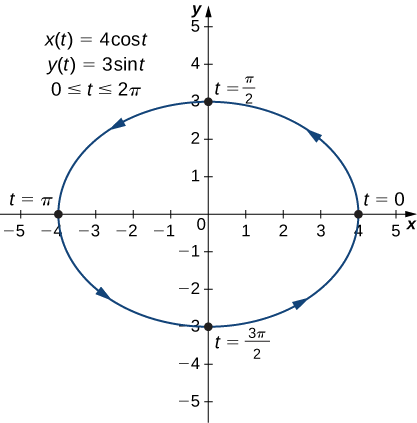
Kama t ikiendelea kutoka\(0\) kwenda\(2π\), hatua juu ya Curve hupitia duaradufu mara moja, katika mwelekeo kinyume. Kumbuka kutoka kwenye kopo ya sehemu kwamba obiti ya Dunia karibu na Jua pia ni elliptical. Huu ni mfano kamili wa kutumia curves parameterized kwa mfano halisi ya ulimwengu uzushi.

Zoezi\(\PageIndex{2}\)

Ondoa parameter ya safu ya ndege iliyoelezwa na equations zifuatazo za parametric na kuelezea grafu inayosababisha.

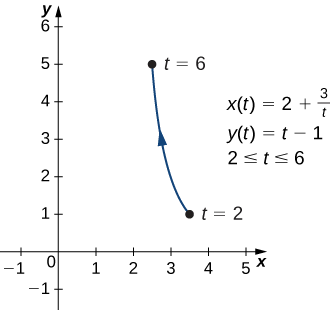
\[ x(t)=2+\dfrac{3}{t}, \quad y(t)=t−1, \quad\text{for }2≤t≤6 \nonumber \]

Kidokezo

Kutatua moja ya milinganyo kwa\(t\) na mbadala katika equation nyingine.

Jibu

\(x=2+\frac{3}{y+1},\)au\(y=−1+\frac{3}{x−2}\). equation hii inaeleza sehemu ya hyperbola mstatili unaozingatia katika\((2,−1)\).

Hadi sasa tumeona njia ya kuondoa parameter, kuchukua tunajua seti ya milinganyo parametric kwamba kuelezea Curve ndege. Nini kama tungependa kuanza na equation ya Curve na kuamua jozi ya milinganyo parametric kwa Curve kwamba? Hii ni hakika inawezekana, na kwa kweli inawezekana kufanya hivyo kwa njia nyingi tofauti kwa Curve kupewa. Mchakato unajulikana kama parameterization ya Curve.

Mfano\(\PageIndex{3}\): Parameterizing a Curve

Kupata jozi mbili tofauti ya milinganyo parametric kuwakilisha grafu ya\(y=2x^2−3\).

Suluhisho

Kwanza, daima inawezekana parameterize Curve kwa kufafanua\(x(t)=t\), kisha kuchukua nafasi\(x\) na\(t\) katika equation kwa\(y(t)\). Hii inatoa parameterization

\[ x(t)=t, \quad y(t)=2t^2−3. \nonumber \]

Kwa kuwa hakuna kizuizi kwenye uwanja katika grafu ya awali, hakuna kizuizi juu ya maadili ya\(t\).

Tuna uhuru kamili katika uchaguzi wa parameterization ya pili. Kwa mfano, tunaweza kuchagua\(x(t)=3t−2\). Kitu pekee tunachohitaji kuangalia ni kwamba hakuna vikwazo vilivyowekwa\(x\); yaani, aina mbalimbali\(x(t)\) ni namba zote halisi. Hii ni kesi kwa\(x(t)=3t−2\). Sasa tangu\(y=2x^2−3\), tunaweza mbadala\(x(t)=3t−2\) kwa ajili ya\(x\). Hii inatoa

\[ y(t)=2(3t−2)^2−2=2(9t^2−12t+4)−2=18t^2−24t+8−2=18t^2−24t+6. \nonumber \]

Kwa hiyo, parameterization ya pili ya Curve inaweza kuandikwa kama

\( x(t)=3t−2\)na\( y(t)=18t^2−24t+6.\)

Zoezi\(\PageIndex{3}\)

Kupata seti mbili tofauti ya milinganyo parametric kuwakilisha grafu ya\(y=x^2+2x\).

Kidokezo

Fuata hatua katika Mfano\(\PageIndex{3}\). Kumbuka tuna uhuru katika kuchagua parameterization kwa\(x(t)\).

Jibu

Uwezekano mmoja ni uwezekano\(x(t)=t, \quad y(t)=t^2+2t.\) mwingine ni\(x(t)=2t−3, \quad y(t)=(2t−3)^2+2(2t−3)=4t^2−8t+3.\) Kuna, kwa kweli, idadi isiyo na kipimo ya uwezekano.

Cycloids na Curves nyingine za paramet

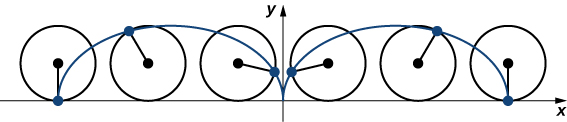
Fikiria kwenda safari ya baiskeli kupitia nchi. Matairi hubakia kuwasiliana na barabara na kugeuka katika muundo unaotabirika. Sasa tuseme ant iliyoamua sana amechoka baada ya siku ndefu na anataka kufika nyumbani. Kwa hiyo hutegemea upande wa tairi na anapata safari ya bure. Njia ambayo ant hii husafiri chini ya barabara moja kwa moja inaitwa cycloid (Kielelezo\( \PageIndex{8}\)). Cycloid yanayotokana na mzunguko (au gurudumu la baiskeli) la radius a hutolewa na usawa wa parametric

\[x(t)=a(t−\sin t), \quad y(t)=a(1−\cos t).\nonumber \]

Ili kuona kwa nini hii ni kweli, fikiria njia ambayo katikati ya gurudumu inachukua. Katikati huenda kando ya\(x\) mhimili kwa urefu wa mara kwa mara sawa na radius ya gurudumu. Ikiwa radius ni\(a\), basi kuratibu za kituo zinaweza kutolewa na equations

\[x(t)=at,\quad y(t)=a\nonumber \]

kwa thamani yoyote ya\(t\). Kisha, fikiria ant, ambayo huzunguka katikati ya njia ya mviringo. Ikiwa baiskeli inahamia kutoka kushoto kwenda kulia basi magurudumu yanazunguka kwa mwelekeo wa saa. Kipimo kinachowezekana cha mwendo wa mviringo wa ant (kuhusiana na katikati ya gurudumu) hutolewa na

\[\begin{align*} x(t) &=−a \sin t \\[4pt] y(t) &=−a\cos t.\end{align*}\]

(Ishara hasi inahitajika ili kurekebisha mwelekeo wa pembe. Ikiwa ishara hasi haikuwepo, tunapaswa kufikiria gurudumu linalozunguka kinyume chake.) Kuongeza equations hizi pamoja hutoa equations kwa cycloid.

\[\begin{align*} x(t) &=a(t−\sin t) \\[4pt] y(t) &=a(1−\cos t ) \end{align*}\]

Kielelezo\(\PageIndex{8}\): Gurudumu kusafiri kando ya barabara bila slipping; uhakika juu ya makali ya gurudumu athari nje cycloid.

Sasa tuseme kwamba gurudumu baiskeli haina kusafiri kando ya barabara moja kwa moja lakini badala yake hatua pamoja ndani ya gurudumu kubwa, kama katika Kielelezo\( \PageIndex{9}\). Katika grafu hii, mduara wa kijani unasafiri karibu na mduara wa bluu kwa mwelekeo wa kinyume. Hatua juu ya makali ya mduara wa kijani huonyesha grafu nyekundu, inayoitwa hypocycloid.

Kielelezo\(\PageIndex{9}\): Grafu ya hypocycloid iliyoelezwa na equations parametric iliyoonyeshwa.

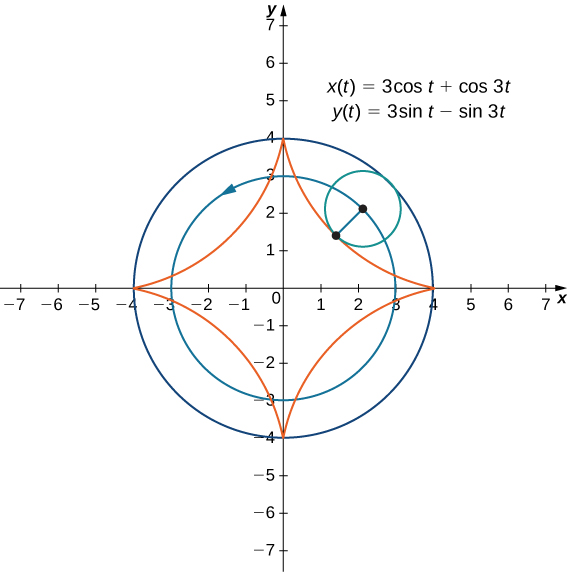
Equations ya jumla ya parametric kwa hypocycloid ni

\[x(t)=(a−b) \cos t+b \cos (\dfrac{a−b}{b})t \nonumber \]

\[y(t)=(a−b) \sin t−b \sin (\dfrac{a−b}{b})t. \nonumber \]

Equations hizi ni ngumu zaidi, lakini derivation ni sawa na equations kwa cycloid. Katika kesi hii sisi kudhani radius ya mduara kubwa ni\(a\) na radius ya mduara ndogo ni\(b\). Kisha katikati ya gurudumu husafiri kando ya mduara wa Radius Ukweli\(a−b.\) huu unaelezea muda wa kwanza katika kila equation hapo juu. Kipindi cha kazi ya pili ya trigonometric katika wote\(x(t)\) na\(y(t)\) ni sawa na\(\dfrac{2πb}{a−b}\).

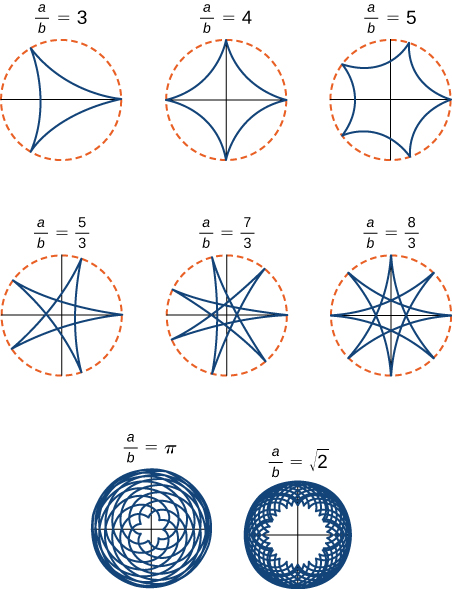
Uwiano\(\dfrac{a}{b}\) unahusiana na idadi ya cusps kwenye grafu (cusps ni pembe au mwisho wa grafu), kama ilivyoonyeshwa kwenye Mchoro\( \PageIndex{10}\). Uwiano huu unaweza kusababisha grafu zenye kuvutia sana, kulingana na kuwa uwiano ni wa busara. Kielelezo\(\PageIndex{9}\) sambamba\(a=4\) na\(b=1\). Matokeo yake ni hypocycloid yenye cusps nne. Kielelezo\(\PageIndex{10}\) kinaonyesha uwezekano mwingine. Hypocycloids mbili za mwisho zina maadili yasiyo ya maana kwa\(\dfrac{a}{b}\). Katika kesi hizi hypocycloids zina idadi isiyo na kipimo cha cusps, hivyo hawarudi kwenye hatua yao ya mwanzo. Hizi ni mifano ya kile kinachojulikana kama curves ya kujaza nafasi.

Kielelezo\(\PageIndex{10}\): Grafu ya hypocycloids mbalimbali sambamba na maadili tofauti ya\(a/b\).

Mchawi wa Agnesi

Vipande vingi vya ndege katika hisabati vinatajwa baada ya watu waliowachunguza kwanza, kama folium ya Descartes au ond ya Archimedes. Hata hivyo, labda jina la ajabu kwa curve ni mchawi wa Agnesi. Kwa nini mchawi?

Maria Gaetana Agnesi (1718—1799) alikuwa mmoja kati ya wanawake wachache wanahisabati waliotambuliwa wa Italia ya karne kumi na nane. Aliandika kitabu maarufu juu ya jiometri ya uchambuzi, iliyochapishwa mwaka wa 1748, ambayo ilijumuisha safu ya kuvutia ambayo ilikuwa imejifunza na Fermat mwaka wa 1630. Mtaalamu wa hisabati Guido Grandi alionyesha mwaka 1703 jinsi ya kujenga pembe hii, ambayo baadaye aliita “versoria,” neno la Kilatini kwa kamba iliyotumiwa katika meli. Agnesi alitumia neno la Kiitaliano kwa kamba hii, “versiera,” lakini kwa Kilatini, neno hili lile linamaanisha “goblin ya kike.” Wakati kitabu cha Agnesi kilitafsiriwa kwa Kiingereza mwaka 1801, mtafsiri alitumia neno “mchawi” kwa pembe, badala ya kamba. Jina “Mchawi wa Agnesi” limekwama tangu wakati huo.

Mchawi wa Agnesi ni Curve inavyoelezwa kama ifuatavyo: Anza na mduara wa Radius a ili pointi\((0,0)\) na\((0,2a)\) ni pointi kwenye mduara (Kielelezo\( \PageIndex{11}\)). Hebu O kuashiria asili. Chagua hatua nyingine yoyote A kwenye mduara, na kuteka mstari wa salama OA. Hebu B ionyeshe hatua ambayo mstari wa OA unaingilia mstari wa usawa kupitia\((0,2a)\). Mstari wa wima kupitia B hupitia mstari wa usawa kupitia A kwenye hatua P. kama hatua A inatofautiana, njia ambayo hatua P husafiri ni mchawi wa Agnesi Curve kwa mduara uliopewa.

Mchawi wa magnesi curves wana maombi katika fizikia, ikiwa ni pamoja na mfano wa mawimbi ya maji na mgawanyo wa mistari ya spectral. Katika nadharia ya uwezekano, Curve inaelezea uwezekano wiani kazi ya usambazaji Cauchy. Katika mradi huu utakuwa parameterize curves hizi.

Kielelezo\(\PageIndex{11}\): Kama\(A\) hatua inavyozunguka mduara, hatua\(P\) inaelezea mchawi wa Agnesi Curve kwa mduara uliopewa.

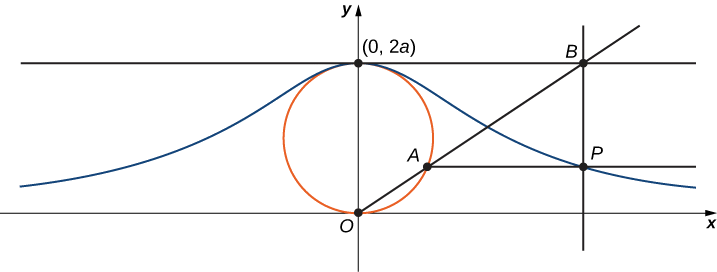
1. Kwenye takwimu, lebo alama zifuatazo, urefu, na angle:

a.\(C\) ni hatua juu ya\(x\) -axis na sawa\(x\) -kuratibu kama\(A\).

b.\(x\) ni\(x\) -kuratibu ya\(P\), na\(y\) ni\(y\) -kuratibu ya\(P\).

c.\(E\) ni hatua\((0,a)\).

d.\(F\) ni hatua kwenye sehemu ya mstari\(OA\) kama sehemu ya mstari\(EF\) ni perpendicular kwa sehemu ya mstari\(OA\).

e.\(b\) ni umbali kutoka\(O\) kwa\(F\).

f.\(c\) ni umbali kutoka\(F\) kwa\(A\).

g.\(d\) ni umbali kutoka\(O\) kwa\(C\).

h.\(θ\) ni kipimo cha angle\(∠COA\).

Lengo la mradi huu ni parameterize mchawi kutumia\(θ\) kama parameter. Ili kufanya hivyo, weka equations kwa\(x\) na\(y\) kwa suala la tu\(θ\).

2. Onyesha hilo\(d=\dfrac{2a}{\sin θ}\).

3. Kumbuka kwamba\(x=d\cos θ\). Onyesha hilo\(x=2a\cot θ\). Unapofanya hivyo, utakuwa na parameterized\(x\) -kuratibu ya Curve kuhusiana na\(θ\). Kama unaweza kupata equation sawa kwa\(y\), utakuwa na parameterized Curve.

4. Kwa upande wa\(θ\), angle ni nini\(∠EOA\)?

5. Onyesha hilo\(b+c=2a\cos\left(\frac{π}{2}−θ\right)\).

6. Onyesha hilo\(y=2a\cos\left(\frac{π}{2}−θ\right)\sin θ\).

7. Onyesha hilo\(y=2a\sin^2θ\). Sasa una parameterized\(y\) -kuratibu ya Curve kuhusiana na\(θ\).

8. Kuhitimisha kuwa parameterization ya kupewa mchawi Curve ni

\[x=2a\cot θ, \quad y=2a \sin^2θ, \quad\text{for }−∞<θ<∞. \nonumber \]

9. Matumizi parameterization yako kuonyesha kwamba kupewa mchawi Curve ni grafu ya kazi\(f(x)=\dfrac{8a^3}{x^2+4a^2}\).

Safari na Ant yangu: Curtate na Prolate Cycloids

Mapema katika sehemu hii, tuliangalia equations parametric kwa cycloid, ambayo ni njia ya uhakika juu ya makali ya athari gurudumu kama gurudumu Rolls kando ya njia moja kwa moja. Katika mradi huu tunaangalia tofauti mbili tofauti za cycloid, inayoitwa cycloids ya curtate na prolate.

Kwanza, hebu tupate upya upya wa usawa wa parametric kwa cycloid. Kumbuka kwamba sisi kuchukuliwa ant stenacious kujaribu kupata nyumbani kwa kunyongwa kwenye makali ya tairi baiskeli. Tumefikiri ant alipanda kwenye tairi kwa makali sana, ambapo tairi inagusa ardhi. Kama gurudumu linaendelea, ant huenda kwa makali ya tairi (Kielelezo\(\PageIndex{12}\)).

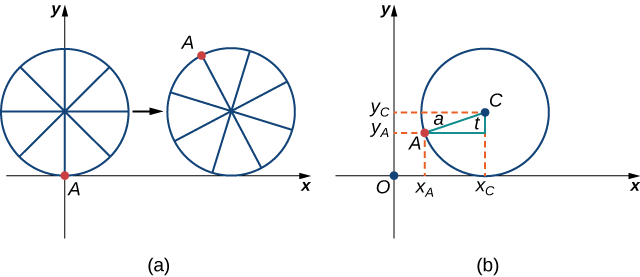
Kama tulivyojadiliwa, tuna mengi ya kubadilika wakati parameterizing Curve. Katika kesi hii sisi basi parameter yetu kuwakilisha angle tairi imezungushwa kupitia. Kuangalia Kielelezo\( \PageIndex{12}\), tunaona kwamba baada ya tairi ina kuzungushwa kwa njia ya angle ya\(t\), nafasi ya katikati ya gurudumu\(C=(x_C,y_C)\), imetolewa na

\(x_C=at\)na\(y_C=a\).

Aidha, kuruhusu\(A=(x_A,y_A)\) kuashiria nafasi ya ant, tunaona kwamba

\(x_C−x_A=a\sin t\)na\(y_C−y_A=a \cos t\)

Kisha

\[x_A=x_C−a\sin t=at−a\sin t=a(t−\sin t) \nonumber \]

\[y_A=y_C−a\cos t=a−a\cos t=a(1−\cos t). \nonumber \]

Kielelezo\(\PageIndex{12}\): (a) Ant huunganisha makali ya tairi ya baiskeli kama gurudumu linaendelea chini. (b) Kutumia jiometri kuamua nafasi ya ant baada ya tairi ina kuzungushwa kwa njia ya angle ya\(t\).

Kumbuka kwamba haya ni sawa parametric uwakilishi tulikuwa kabla, lakini sisi sasa kupewa maana ya kimwili kwa variable parametric\(t\).

Baada ya muda ant ni kupata kizunguzungu kutoka kwenda pande zote na pande zote makali ya tairi. Kwa hiyo anapanda moja ya spokes kuelekea katikati ya gurudumu. Kwa kupanda kuelekea katikati ya gurudumu, ant imebadilisha njia yake ya mwendo. Njia mpya ina mwendo mdogo wa juu-na-chini na inaitwa cycloid ya curtate (Kielelezo\( \PageIndex{13}\)). Kama inavyoonekana katika takwimu, sisi basi b kuashiria umbali pamoja alizungumza kutoka katikati ya gurudumu kwa ant. Kama hapo awali, tunaruhusu kuwakilisha angle tairi imezunguka. Zaidi ya hayo,\(C=(x_C,y_C)\) tunaruhusu kuwakilisha nafasi ya katikati ya gurudumu na\(A=(x_A,y_A)\) kuwakilisha nafasi ya ant.

Kielelezo\(\PageIndex{13}\): (a) Ant hupanda moja ya spokes kuelekea katikati ya gurudumu. (b) Njia ya chungu ya mwendo baada ya kupanda karibu na katikati ya gurudumu. Hii inaitwa cycloid curtate. (c) kuanzisha mpya, sasa kwa kuwa chungu amehamia karibu na katikati ya gurudumu.

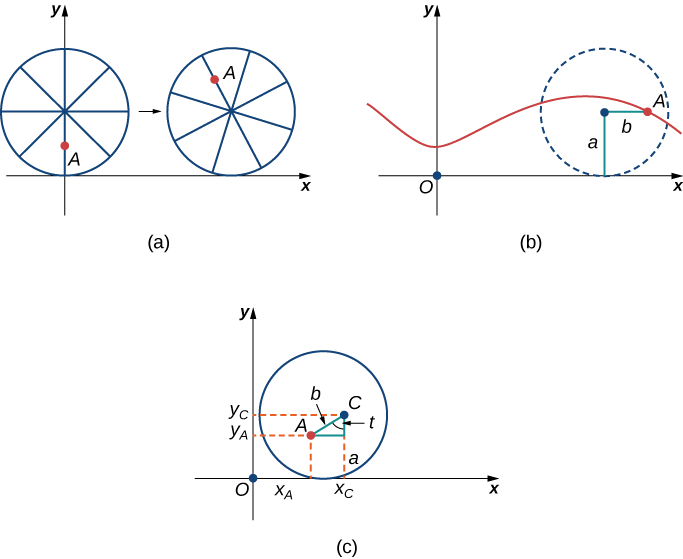
1. ni nafasi ya katikati ya gurudumu baada ya tairi ina kuzungushwa kwa njia ya angle ya\(t\)?

2. Tumia jiometri ili kupata maneno kwa\(x_C−x_A\) na kwa\(y_C−y_A\).

3. Kwa misingi ya majibu yako kwa sehemu ya 1 na 2, ni nini equations parametric inayowakilisha cycloid curtate?

Mara baada ya kichwa cha ant kinafuta, anajua kwamba bicyclist amefanya kugeuka, na sasa anasafiri mbali na nyumba yake. Kwa hiyo anatupa tairi ya baiskeli na inaonekana karibu. Kwa bahati nzuri, kuna seti ya tracks treni karibu, inaongozwa nyuma katika mwelekeo sahihi. Hivyo ant inaongoza juu ya treni tracks kusubiri. Baada ya muda, treni inakwenda, akielekea kwenye mwelekeo sahihi, na anaweza kuruka juu na kukamata tu makali ya gurudumu la treni (bila kupata squished!).

Ant bado ana wasiwasi juu ya kupata kizunguzungu, lakini gurudumu la treni ni slippery na hana spokes kupanda, hivyo anaamua tu hutegemea makali ya gurudumu na matumaini ya bora. Sasa, magurudumu ya treni yana flange ya kuweka gurudumu kukimbia kwenye nyimbo. Kwa hiyo, katika kesi hii, kwa kuwa ant hutegemea makali ya flange, umbali kutoka katikati ya gurudumu hadi kwenye ant ni kweli zaidi kuliko eneo la gurudumu (Kielelezo\(\PageIndex{14}\)).

kuanzisha hapa kimsingi ni sawa na wakati chungu akapanda alizungumza juu ya gurudumu baiskeli. Tunaruhusu b kutaja umbali kutoka katikati ya gurudumu hadi kwenye ant, na tunaruhusu kuwakilisha angle ambayo tairi imezunguka. Zaidi ya hayo,\(C=(x_C,y_C)\) tunaruhusu kuwakilisha nafasi ya katikati ya gurudumu na\(A=(x_A,y_A)\) kuwakilisha nafasi ya ant (Kielelezo\( \PageIndex{14}\)).

Wakati umbali kutoka katikati ya gurudumu hadi kwenye ant ni kubwa zaidi kuliko eneo la gurudumu, njia yake ya mwendo inaitwa cycloid ya prolate. Grafu ya cycloid ya prolate inavyoonyeshwa kwenye takwimu.

Kielelezo\(\PageIndex{14}\): (a) Ant hutegemea kwenye flange ya gurudumu la treni. (b) kuanzisha mpya, sasa kwamba ant imeongezeka kwenye gurudumu la treni. (c) Ant husafiri pamoja na cycloid ya prolate.

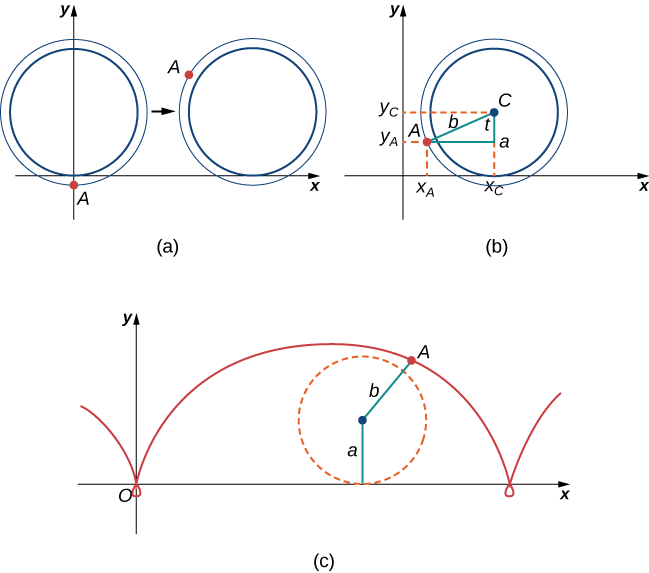
4. Kutumia mbinu hiyo kutumika katika sehemu 1 - 3, kupata equations parametric kwa njia ya mwendo wa ant.

5. Unaona nini kuhusu jibu lako kwa sehemu ya 3 na jibu lako kwa sehemu ya 4?

Kumbuka kwamba ant ni kweli kusafiri nyuma wakati mwingine (“loops” katika grafu), ingawa treni inaendelea kusonga mbele. Yeye pengine ni kwenda kuwa kweli kizunguzungu na wakati anapata nyumbani!

Dhana muhimu

• Ulinganisho wa parametric hutoa njia rahisi ya kuelezea safu. Kipimo kinaweza kuwakilisha muda au kiasi kingine cha maana.
• Mara nyingi inawezekana kuondokana na parameter katika Curve parameterized kupata kazi au uhusiano kuelezea kwamba Curve.
• Kuna daima zaidi ya njia moja ya parameterize Curve.
• Ulinganifu wa parametric unaweza kuelezea curves ngumu ambazo ni vigumu au labda haiwezekani kuelezea kutumia kuratibu mstatili.

faharasa

cycloid

Curve kufuatiliwa na uhakika juu ya mdomo wa gurudumu mviringo kama mistari gurudumu pamoja mstari wa moja kwa moja bila slippage.

ncha

mwisho au sehemu ambapo curves mbili hukutana

mwelekeo

mwelekeo ambao hatua huenda kwenye grafu kama parameter inavyoongezeka

parameter

variable huru kwamba wote\(x\) na\(y\) hutegemea katika Curve parametric; kawaida inawakilishwa na variable\(t\)

parametric curve

grafu ya equations parametric\(x(t)\) na\(y(t)\) zaidi ya muda\(a≤t≤b\) pamoja na equations

milinganyo ya parametric

equations\(x=x(t)\) na\(y=y(t)\) kwamba kufafanua Curve parametric

parameterization ya curve

kuandika upya equation ya Curve inavyoelezwa na kazi\(y=f(x)\) kama milinganyo parametric