Skip to main content
Global

10.2E: Mazoezi ya Sehemu ya 10.2

  1. Last updated
  2. Save as PDF
  • Page ID
    178082

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1) Kama\(\displaystyle f(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) na\(\displaystyle g(x)=\sum_{n=0}^∞(−1)^n\frac{x^n}{n!}\), kupata nguvu mfululizo wa\(\frac{1}{2}\big(f(x)+g(x)\big)\) na ya\(\frac{1}{2}\big(f(x)−g(x)\big)\).

    Jibu
    \(\displaystyle \frac{1}{2}\big(f(x)+g(x)\big)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\)na\(\displaystyle \frac{1}{2}\big(f(x)−g(x)\big)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\).

    2) Kama\(\displaystyle C(x)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) na\(\displaystyle S(x)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\), kupata nguvu mfululizo wa\(C(x)+S(x)\) na ya\(C(x)−S(x)\).

    Katika mazoezi ya 3 - 6, tumia sehemu ndogo ili kupata mfululizo wa nguvu wa kila kazi.

    3)\(\dfrac{4}{(x−3)(x+1)}\)

    Jibu
    \(\displaystyle \frac{4}{(x−3)(x+1)}=\frac{1}{x−3}−\frac{1}{x+1}=−\frac{1}{3(1−\frac{x}{3})}−\frac{1}{1−(−x)}=−\frac{1}{3}\sum_{n=0}^∞\left(\frac{x}{3}\right)^n−\sum_{n=0}^∞(−1)^nx^n=\sum_{n=0}^∞\left((−1)^{n+1}−\frac{1}{3n+1}\right)x^n\)

    4)\(\dfrac{3}{(x+2)(x−1)}\)

    5)\(\dfrac{5}{(x^2+4)(x^2−1)}\)

    Jibu
    \(\displaystyle \frac{5}{(x^2+4)(x^2−1)}=\frac{1}{x^2−1}−\frac{1}{4}\frac{1}{1+\left(\frac{x}{2}\right)^2}=−\sum_{n=0}^∞x^{2n}−\frac{1}{4}\sum_{n=0}^∞(−1)^n\left(\frac{x}{2}\right)^n=\sum_{n=0}^∞\left((−1)+(−1)^{n+1}\frac{1}{2^{n+2}}\right)x^{2n}\)

    6)\(\dfrac{30}{(x^2+1)(x^2−9)}\)

    Katika mazoezi ya 7 - 10, onyesha kila mfululizo kama kazi ya busara.

    7)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^n}\)

    Jibu
    \(\displaystyle \frac{1}{x}\sum_{n=0}^∞\frac{1}{x^n}=\frac{1}{x}\cdot \frac{1}{1−\frac{1}{x}}=\frac{1}{x−1}\)

    8)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^{2n}}\)

    9)\(\displaystyle \sum_{n=1}^∞\frac{1}{(x−3)^{2n−1}}\)

    Jibu
    \(\displaystyle \frac{1}{x−3}\cdot \frac{1}{1−\frac{1}{(x−3)^2}}=\frac{x−3}{(x−3)^2−1}\)

    10)\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{(x−3)^{2n−1}}−\frac{1}{(x−2)^{2n−1}}\right)\)

    Mazoezi 11 - 16 kuchunguza maombi ya annuities.

    11) Tumia mahesabu\(P\) ya sasa ya annuity ambayo $10,000 inapaswa kulipwa kila mwaka kwa kipindi cha miaka 20, kuchukua viwango vya riba\(r=0.03,\, r=0.05\), na\(r=0.07\).

    Jibu
    \(P=P_1+⋯+P_{20}\)wapi\(P_k=10,000\dfrac{1}{(1+r)^k}\). Kisha\(\displaystyle P=10,000\sum_{k=1}^{20}\frac{1}{(1+r)^k}=10,000\frac{1−(1+r)^{−20}}{r}\). Wakati\(r=0.03, \,P≈10,000×14.8775=148,775.\) Wakati\(r=0.05, \,P≈10,000×12.4622=124,622.\) Wakati\(r=0.07, \, P≈105,940\).

    12) Kuhesabu maadili ya sasa\(P\) ya annuities ambayo $9,000 ni kulipwa nje kila mwaka daima, kuchukua viwango vya riba ya\(r=0.03,\, r=0.05\) na\(r=0.07\).

    13) Mahesabu payouts ya kila mwaka kutolewa\(C\) kwa ajili ya 20 miaka juu ya annuities kuwa thamani ya sasa $100,000 kuchukua viwango vya riba husika ya\(r=0.03,\, r=0.05,\) na\(r=0.07.\)

    Jibu
    Kwa ujumla,\(P=\dfrac{C(1−(1+r)^{−N})}{r}\) kwa\(N\) miaka ya payouts, au\(C=\dfrac{Pr}{1−(1+r)^{−N}}\). Kwa\(N=20\) na\(P=100,000\), mtu ana\(C=6721.57\)\(r=0.03; \, C=8024.26\) wakati\(r=0.05\); na\(C≈9439.29\) wakati\(r=0.07\).

    14) Mahesabu payouts\(C\) ya kila mwaka ya kutolewa daima juu ya annuities kuwa thamani ya sasa $100,000 kuchukua viwango vya riba husika ya\(r=0.03, \,r=0.05,\) na\(r=0.07\).

    15) Tuseme kwamba annuity ina thamani ya sasa dola\(P=1\) milioni. Nini riba\(r\) itaruhusu kwa payouts daima kila mwaka ya $50,000?

    Jibu
    Kwa ujumla,\(P=\dfrac{C}{r}.\) Hivyo,\(r=\dfrac{C}{P}=5×\frac{10^4}{10^6}=0.05.\)

    16) Tuseme kwamba annuity ina thamani ya sasa dola\(P=10\) milioni. Nini riba\(r\) bila kuruhusu kwa payouts daima kila mwaka ya $100,000?

    Katika mazoezi 17 - 20, onyesha jumla ya kila mfululizo wa nguvu kwa suala la mfululizo wa kijiometri, na kisha ueleze jumla kama kazi ya busara.

    17)\(x+x^2−x^3+x^4+x^5−x^6+⋯\) (kidokezo: Mamlaka ya kikundi\(x^{3k}, \, x^{3k−1},\) na\(x^{3k−2}\).)

    Jibu
    \((x+x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x+x^2−x^3}{1−x^3}\)

    18)\(x+x^2−x^3−x^4+x^5+x^6−x^7−x^8+⋯\) (kidokezo: Mamlaka ya kikundi\(x^{4k}, \, x^{4k−1},\) nk)

    19)\(x−x^2−x^3+x^4−x^5−x^6+x^7−⋯\) (kidokezo: nguvu Group\(x^{3k}, \, x^{3k−1}\), na\(x^{3k−2}\).)

    Jibu
    \((x−x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x−x^2−x^3}{1−x^3}\)

    20)\(\displaystyle \frac{x}{2}+\frac{x^2}{4}−\frac{x^3}{8}+\frac{x^4}{16}+\frac{x^5}{32}−\frac{x^6}{64}+⋯\) (kidokezo: Mamlaka ya kikundi\(\left(\dfrac{x}{2}\right)^{3k}, \, \left(\dfrac{x}{2}\right)^{3k−1},\) na\(\left(\dfrac{x}{2}\right)^{3k−2}\).)

    Katika mazoezi 21 - 24, pata mfululizo wa nguvu wa\(f(x)g(x)\) kutolewa\(f\) na\(g\) kama ilivyoelezwa.

    21)\(\displaystyle f(x)=2\sum_{n=0}^∞x^n,g(x)=\sum_{n=0}^∞nx^n\)

    Jibu
    \(a_n=2, \, b_n=n\)hivyo\(\displaystyle c_n=\sum_{k=0}^nb_ka_{n−k}=2\sum_{k=0}^nk=(n)(n+1)\) na\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(n+1)x^n\)

    22)\(\displaystyle f(x)=\sum_{n=1}^∞x^n,\; g(x)=\sum_{n=1}^∞\frac{1}{n}x^n\). Eleza coefficients ya\(f(x)g(x)\) katika suala la\(\displaystyle H_n=\sum_{k=1}^n\frac{1}{k}\).

    23)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞\left(\frac{x}{2}\right)^n\)

    Jibu
    \(a_n=b_n=2^{−n}\)hivyo\(\displaystyle c_n=\sum_{k=1}^nb_ka_{n−k}=2^{−n}\sum_{k=1}^n1=\frac{n}{2^n}\) na\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n\left(\frac{x}{2}\right)^n\)

    24)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞nx^n\)

    Katika mazoezi ya 25 - 26, kutofautisha mfululizo uliopewa upanuzi wa muda\(f\) kwa muda ili kupata upanuzi wa mfululizo unaofanana kwa derivative ya\(f.\)

    25)\(\displaystyle f(x)=\frac{1}{1+x}=\sum_{n=0}^∞(−1)^nx^n\)

    Jibu
    derivative ya\(f\) ni\(\displaystyle −\frac{1}{(1+x)^2}=−\sum_{n=0}^∞(−1)^n(n+1)x^n\).

    26)\(\displaystyle f(x)=\frac{1}{1−x^2}=\sum_{n=0}^∞x^{2n}\)

    Katika mazoezi 27-28, kuunganisha kutokana mfululizo upanuzi wa muda\(f\) kwa muda kutoka sifuri\(x\) ili kupata sambamba mfululizo upanuzi kwa muda usiojulikana muhimu ya\(f\).

    27)\(\displaystyle f(x)=\frac{2x}{(1+x^2)^2}=\sum_{n=1}^∞(−1)^n(2n)x^{2n−1}\)

    Jibu
    muhimu kwa muda usiojulikana\(f\) ni\(\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}\).

    28)\(\displaystyle f(x)=\frac{2x}{1+x^2}=2\sum_{n=0}^∞(−1)^nx^{2n+1}\)

    Katika mazoezi 29 - 32, tathmini kila mfululizo usio na kipimo kwa kutambua kama thamani ya derivative au muhimu ya mfululizo wa kijiometri.

    29) Tathmini\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}\) kama\(f′\left(\frac{1}{2}\right)\) wapi\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

    Jibu
    \(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f′(\frac{1}{2})=\sum_{n=1}^∞\frac{n}{2^{n−1}}=\frac{d}{dx}(1−x)^{−1}\Big|_{x=1/2}=\frac{1}{(1−x)^2}\Big|_{x=1/2}=4\)hivyo\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}=2.\)

    30) Tathmini\(\displaystyle \sum_{n=1}^∞\frac{n}{3^n}\) kama\(f′\left(\frac{1}{3}\right)\) wapi\(\displaystyle f(x)=\sum_{n=0}^∞x^{6n}\).

    31) Tathmini\(\displaystyle \sum_{n=2}^∞\frac{n(n−1)}{2^n}\) kama\(f''\left(\frac{1}{2}\right)\) wapi\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

    Jibu
    \(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f''\left(\frac{1}{2}\right)=\sum_{n=2}^∞\frac{n(n−1)}{2^{n−2}}=\frac{d^2}{dx^2}(1−x)^{−1}\Big|_{x=1/2}=\frac{2}{(1−x)^3}\Big|_{x=1/2}=16\)hivyo\(\displaystyle \sum_{n=2}^∞n\frac{(n−1)}{2^n}=4.\)

    32) Tathmini\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n}{n+1}\) kama\(\displaystyle ∫^1_0f(t) \, dt\) wapi\(\displaystyle f(x)=\sum_{n=0}^∞(−1)^nx^{2n}=\frac{1}{1+x^2}\).

    Katika mazoezi 33 - 39, kutokana na kwamba\(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\), tumia upambanuzi wa muda mrefu au ushirikiano ili kupata mfululizo wa nguvu kwa kila kazi unaozingatia katika hatua iliyotolewa.

    33)\(f(x)=\ln x\) unaozingatia\(x=1\) (kidokezo:\(x=1−(1−x)\))

    Jibu
    \(\displaystyle ∫\sum(1−x)^n\,dx=∫\sum(−1)^n(x−1)^n\,dx=\sum \frac{(−1)^n(x−1)^{n+1}}{n+1}\)

    34)\(\ln(1−x)\) saa\(x=0\)

    35)\(\ln(1−x^2)\) saa\(x=0\)

    Jibu
    \(\displaystyle −∫^{x^2}_{t=0}\frac{1}{1−t}dt=−\sum_{n=0}^∞∫^{x^2}_0t^ndx−\sum_{n=0}^∞\frac{x^{2(n+1)}}{n+1}=−\sum_{n=1}^∞\frac{x^{2n}}{n}\)

    36)\(f(x)=\dfrac{2x}{(1−x^2)^2}\) saa\(x=0\)

    37)\(f(x)=\tan^{−1}(x^2)\) saa\(x=0\)

    Jibu
    \(\displaystyle ∫^{x^2}_0\frac{dt}{1+t^2}=\sum_{n=0}^∞(−1)^n∫^{x^2}_0t^{2n}dt=\sum_{n=0}^∞(−1)^n\frac{t^{2n+1}}{2n+1}∣^{x^2}_{t=0}=\sum_{n=0}^∞(−1)^n\frac{x^{4n+2}}{2n+1}\)

    38)\(f(x)=\ln(1+x^2)\) katika\(x=0\)

    39)\(\displaystyle f(x)=∫^x_0\ln t\,dt\) wapi\(\displaystyle \ln(x)=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^n}{n}\)

    Jibu
    Muda kwa muda muungano anatoa\(\displaystyle ∫^x_0\ln t\,dt=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^{n+1}}{n(n+1)}=\sum_{n=1}^∞(−1)^{n−1}\left(\frac{1}{n}−\frac{1}{n+1}\right)(x−1)^{n+1}=(x−1)\ln x+\sum_{n=2}^∞(−1)^n\frac{(x−1)^n}{n}=x\ln x−x.\)

    40) [T] Kutathmini nguvu mfululizo upanuzi\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\) katika\(x=1\) kuonyesha kwamba\(\ln(2)\) ni jumla ya alternating mfululizo harmonic. Matumizi alternating mfululizo mtihani kuamua jinsi wengi suala la jumla zinahitajika kukadiria\(\ln(2)\) sahihi kwa ndani\(0.001,\) na kupata makadirio hayo.

    41) [T] Ondoa mfululizo usio wa\(\ln(1−x)\) kutoka\(\ln(1+x)\) kupata nguvu mfululizo kwa\(\ln\left(\dfrac{1+x}{1−x}\right)\). Tathmini saa\(x=\frac{1}{3}\). Je, ni ndogo\(N\) zaidi kwamba jumla ya\(N^{\text{th}}\) sehemu ya mfululizo huu inakaribia\(\ln(2)\) na kosa chini ya\(0.001\)?

    Jibu
    Tuna\(\displaystyle \ln(1−x)=−\sum_{n=1}^∞\frac{x^n}{n}\) hivyo\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\). Hivyo,\(\displaystyle \ln\left(\frac{1+x}{1−x}\right)=\sum_{n=1}^∞\big(1+(−1)^{n−1}\big)\frac{x^n}{n}=2\sum_{n=1}^∞\frac{x^{2n−1}}{2n−1}\). Wakati\(x=\frac{1}{3}\) sisi kupata\(\displaystyle \ln(2)=2\sum_{n=1}^∞\frac{1}{3^{2n−1}(2n−1)}\). Tuna\(\displaystyle 2\sum_{n=1}^3\frac{1}{3^{2n−1}(2n−1)}=0.69300…\), wakati\(\displaystyle 2\sum_{n=1}^4\frac{1}{3^{2n−1}(2n−1)}=0.69313…\) na\(\ln(2)=0.69314…;\) kwa hiyo,\(N=4\).

    Katika mazoezi 42 - 45, kwa kutumia badala ikiwa imeonyeshwa, onyesha kila mfululizo kwa suala la kazi za msingi na kupata radius ya kuunganishwa kwa jumla.

    42)\(\displaystyle \sum_{k=0}^∞(x^k−x^{2k+1})\)

    43)\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}\)

    Jibu
    \(\displaystyle \sum_{k=1}^∞\frac{x^k}{k}=−\ln(1−x)\)hivyo\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}=−\frac{1}{6}\ln(1−x^3)\). Radi ya kuunganisha ni sawa\(1\) na mtihani wa uwiano.

    44)\(\displaystyle \sum_{k=1}^∞(1+x^2)^{−k}\) kutumia\(y=\dfrac{1}{1+x^2}\)

    45)\(\displaystyle \sum_{k=1}^∞2^{−kx}\) kutumia\(y=2^{−x}\)

    Jibu
    Ikiwa\(y=2^{−x}\), basi\(\displaystyle \sum_{k=1}^∞y^k=\frac{y}{1−y}=\frac{2^{−x}}{1−2^{−x}}=\frac{1}{2^x−1}\). Ikiwa\(a_k=2^{−kx}\), basi\(\dfrac{a_{k+1}}{a_k}=2^{−x}<1\) wakati\(x>0\). Hivyo mfululizo hujiunga kwa wote\(x>0\).

    46) Onyesha kwamba, hadi mamlaka\(x^3\) na\(y^3\),\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) hutimiza\(E(x+y)=E(x)E(y)\).

    47) Tofautisha mfululizo\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) mrefu kwa muda ili kuonyesha kwamba\(E(x)\) ni sawa na derivative yake.

    Jibu
    Majibu yatatofautiana.

    48) Onyesha kwamba ikiwa\(\displaystyle f(x)=\sum_{n=0}^∞a_nx^n\) ni jumla ya nguvu hata, yaani,\(a_n=0\) ikiwa\(n\) ni isiyo ya kawaida, basi\(\displaystyle F=∫^x_0f(t)\, dt\) ni jumla ya nguvu isiyo ya kawaida, wakati ikiwa\(I\) ni jumla ya nguvu isiyo ya kawaida, basi\(F\) ni jumla ya nguvu hata.

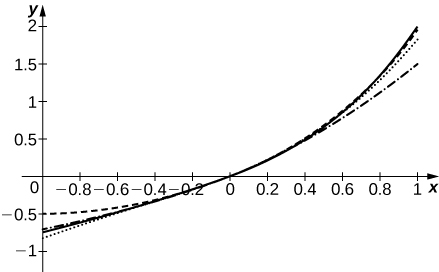
    49) [T] Tuseme kwamba coefficients na ya mfululizo\(\displaystyle \sum_{n=0}^∞a_nx^n\) hufafanuliwa na uhusiano wa kurudia\(a_n=\dfrac{a_{n−1}}{n}+\dfrac{a_{n−2}}{n(n−1)}\). Kwa\(a_0=0\) na\(a_1=1\), compute na njama kiasi kwa\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) ajili ya\(N=2,3,4,5\) juu\([−1,1].\)

    Jibu

    Curve imara ni\(S_5\). Curve dashed ni\(S_2\), dotted ni\(S_3\), na dash-dotted ni\(S_4\)

    Hii ni grafu ya curves tatu. Wote wanaongezeka na kuwa karibu sana kama njia ya curves x = 0. Kisha hutenganisha kama x hatua mbali na 0.

    50) [T] Tuseme kwamba coefficients an ya mfululizo\(\displaystyle \sum_{n=0}^∞a_nx^n\) hufafanuliwa na uhusiano upprepning\(a_n=\dfrac{a_{n−1}}{\sqrt{n}}−\dfrac{a_{n−2}}{\sqrt{n(n−1)}}\). Kwa\(a_0=1\) na\(a_1=0\), kukokotoa na njama kiasi kwa\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) ajili ya\(N=2,3,4,5\) juu ya\([−1,1]\).

    51) [T] Kutokana nguvu mfululizo upanuzi\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\), kuamua jinsi wengi suala\(N\) la jumla tathmini katika\(x=−1/2\) zinahitajika kwa takriban\(\ln(2)\) sahihi ndani\(1/1000.\) Tathmini sambamba sehemu jumla\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{x^n}{n}\).

    Jibu
    Wakati\(\displaystyle x=−\frac{1}{2}, \;−\ln(2)=\ln\left(\frac{1}{2}\right)=−\sum_{n=1}^∞\frac{1}{n2^n}\). Kwa kuwa\(\displaystyle \sum^∞_{n=11}\frac{1}{n2^n}<\sum_{n=11}^∞\frac{1}{2^n}=\frac{1}{2^{10}},\) moja ina\(\displaystyle \sum_{n=1}^{10}\frac{1}{n2^n}=0.69306…\) ambapo\(\ln(2)=0.69314…;\) kwa hiyo,\(N=10.\)

    52) [T] Kutokana nguvu mfululizo upanuzi\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\), kutumia alternating mfululizo mtihani kuamua jinsi wengi maneno\(N\) ya jumla tathmini katika\(x=1\) zinahitajika kwa takriban\(\tan^{−1}(1)=\frac{π}{4}\) sahihi ndani\(1/1000.\) Tathmini sambamba sehemu jumla\(\displaystyle \sum_{k=0}^N(−1)^k\frac{x^{2k+1}}{2k+1}\).

    53) [T] Kumbuka kwamba\(\tan^{−1}\left(\frac{1}{\sqrt{3}}\right)=\frac{π}{6}.\) Kutokana thamani halisi ya\(\frac{1}{\sqrt{3}})\), makadirio\(\frac{π}{6}\) kwa kutathmini kiasi sehemu\(S_N\left(\frac{1}{\sqrt{3}}\right)\) ya upanuzi nguvu mfululizo\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\) katika\(x=\frac{1}{\sqrt{3}}\). Ni nambari ndogo\(N\) zaidi ambayo\(6S_N\left(\frac{1}{\sqrt{3}}\right)\) inakaribia\(π\) kwa usahihi ndani\(0.001\)? Ni maneno ngapi zinahitajika kwa usahihi ndani\(0.00001\)?

    Jibu
    \(\displaystyle 6S_N\left(\frac{1}{\sqrt{3}}\right)=2\sqrt{3}\sum_{n=0}^N(−1)^n\frac{1}{3^n(2n+1).}\)Moja ina\(π−6S_4\left(\frac{1}{\sqrt{3}}\right)=0.00101…\) na\(π−6S_5\left(\frac{1}{\sqrt{3}}\right)=0.00028…\) hivyo\(N=5\) ni ndogo sehemu jumla kwa usahihi ndani\(0.001.\) Pia,\(π−6S_7\left(\frac{1}{\sqrt{3}}\right)=0.00002…\) wakati\(π−6S_8\left(\frac{1}{\sqrt{3}}\right)=−0.000007…\) hivyo\(N=8\) ni ndogo ya\(N\) kutoa usahihi ndani ya\(0.00001.\)