10.3: Taylor na Maclaurin Series

Malengo ya kujifunza

• Eleza utaratibu wa kutafuta Taylor polynomial ya utaratibu fulani kwa ajili ya kazi.
• Eleza maana na umuhimu wa theorem ya Taylor na salio.
• Makisio salio kwa Taylor mfululizo makadirio ya kazi fulani.

Katika sehemu mbili zilizopita tulijadili jinsi ya kupata uwakilishi wa mfululizo wa nguvu kwa aina fulani za kazi-hasa, kazi zinazohusiana na mfululizo wa kijiometri. Hapa tunazungumzia uwakilishi wa mfululizo wa nguvu kwa aina nyingine za kazi. Hasa, tunashughulikia maswali yafuatayo: Ni kazi gani zinaweza kuwakilishwa na mfululizo wa nguvu na tunawezaje kupata uwakilishi huo? Kama tunaweza kupata nguvu mfululizo uwakilishi kwa ajili ya kazi fulani$f$ na mfululizo converges juu ya baadhi ya muda, jinsi gani sisi kuthibitisha kwamba mfululizo kweli hukutana na$f$?

Maelezo ya jumla ya Taylor/Maclaurin Series

Fikiria kazi$f$ ambayo ina nguvu mfululizo uwakilishi katika$x=a$. Kisha mfululizo una fomu

$$\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+ \dots. \label{eq1}$$

Coefficients lazima iwe nini? Kwa sasa, tunapuuza masuala ya kuungana, lakini badala yake tuzingatia kile mfululizo unapaswa kuwa, ikiwa kuna. Tunarudi kujadili muunganiko baadaye katika sehemu hii. Kama mfululizo Equation\ ref {eq1} ni uwakilishi kwa$f$ saa$x=a$, sisi hakika wanataka mfululizo sawa$f(a)$ katika$x=a$. Kutathmini mfululizo katika$x=a$, tunaona kwamba

$$\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(a−a)+c_2(a−a)^2+\dots=c_0.\label{eq2}$$

Hivyo, mfululizo huo ni sawa$f(a)$ na mgawo$c_0=f(a)$. Aidha, tungependa derivative kwanza ya mfululizo nguvu sawa$f′(a)$ katika$x=a$. Kutofautisha Equation\ ref {eq2} muda kwa muda, tunaona kwamba

$$\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(x−a)+3c_3(x−a)^2+\dots.\label{eq3}$$

Kwa hiyo, katika$x=a,$ derivative ni

$$\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(a−a)+3c_3(a−a)^2+\dots=c_1.\label{eq4}$$

Kwa hiyo, derivative ya mfululizo sawa$f′(a)$ kama mgawo$c_1=f′(a).$ Kuendelea kwa njia hii, tunatafuta coefficients$c_n$ kama vile derivatives yote ya mfululizo wa nguvu Equation\ ref {eq4} itakubaliana na derivatives zote zinazofanana za$f$ at$x=a$. Derivatives ya pili na ya tatu ya Equation\ ref {eq3} hutolewa na

$$\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n \right)=2c_2+3⋅2c_3(x−a)+4⋅3c_4(x−a)^2+\dots\label{eq5}$$

na

$$\dfrac{d^3}{dx^3} \left( \sum_{n=0}^∞c_n(x−a)^n \right)=3⋅2c_3+4⋅3⋅2c_4(x−a)+5⋅4⋅3c_5(x−a)^2+⋯.\label{eq6}$$

Kwa hiyo, saa$x=a$, derivatives pili na ya tatu

$$\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=2c_2+3⋅2c_3(a−a)+4⋅3c_4(a−a)^2+\dots=2c_2\label{eq7}$$

na

$$\dfrac{d^3}{dx^3} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=3⋅2c_3+4⋅3⋅2c_4(a−a)+5⋅4⋅3c_5(a−a)^2+\dots =3⋅2c_3\label{eq8}$$

sawa$f''(a)$ na$f'''(a)$, kwa mtiririko huo, ikiwa$c_2=\dfrac{f''(a)}{2}$ na$c_3=\dfrac{f'''(a)}{3⋅2}$. Kwa ujumla, tunaona kwamba ikiwa$f$ ina uwakilishi wa mfululizo wa nguvu$x=a$, basi coefficients inapaswa kutolewa na$c_n=\dfrac{f^{(n)}(a)}{n!}$. Hiyo ni, mfululizo lazima

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯ \nonumber$$

Mfululizo huu wa nguvu$f$ unajulikana kama mfululizo wa Taylor kwa$f$ saa$a.$ If$x=0$, basi mfululizo huu unajulikana kama mfululizo wa Maclaurin kwa$f$.

Ufafanuzi$\PageIndex{1}$: Maclaurin and Taylor series

Ikiwa$f$ ina derivatives ya amri zote$x=a$, basi mfululizo wa Taylor$f$ kwa kazi$a$ ni

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯ \nonumber$$

Mfululizo wa Taylor kwa$f$ saa 0 unajulikana kama mfululizo wa Maclaurin kwa$f$.

Baadaye katika sehemu hii, tutaonyesha mifano ya kutafuta mfululizo wa Taylor na kujadili hali ambayo mfululizo wa Taylor kwa kazi utakutana na kazi hiyo. Hapa, tunasema matokeo muhimu. Kumbuka kwamba uwakilishi wa mfululizo wa nguvu ni wa kipekee. Kwa hiyo, ikiwa kazi$f$ ina mfululizo wa nguvu$a$, basi ni lazima iwe mfululizo wa Taylor kwa$f$ saa$a$.

Upekee wa Taylor Series

Kama kazi$f$ ina nguvu mfululizo katika kwamba hujiunga na baadhi$f$ ya muda wazi zenye$a$, basi kwamba mfululizo nguvu ni Taylor mfululizo kwa$f$ saa$a$.

ushahidi ifuatavyo moja kwa moja kutoka kwamba kujadiliwa hapo awali.

Kuamua kama mfululizo wa Taylor unajiunga, tunahitaji kuangalia mlolongo wake wa kiasi cha sehemu. Hizi kiasi sehemu ni ya mwisho polynomials, inayojulikana kama Taylor polynomials.

Taylor Polynomials

Jumla ya$n^{\text{th}}$ sehemu ya mfululizo Taylor kwa ajili ya kazi$f$ katika$a$ inajulikana kama$n^{\text{th}}$ -shahada Taylor polynomial. Kwa mfano, 0 ^th, 1 ^st, 2 ^nd, na 3 ^rd kiasi cha sehemu ya mfululizo wa Taylor hutolewa na

$$\begin{align*} p_0(x) &=f(a) \\[4pt] p_1(x) &=f(a)+f′(a)(x−a) \\[4pt]p_2(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2\ \\[4pt]p_3(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3 \end{align*}$$

mtawalia. Hizi kiasi sehemu inajulikana kama 0 ^th, 1 ^st, 2 ^nd, na 3 ^rd shahada Taylor polynomials ya$f$ at$a$, kwa mtiririko huo. Ikiwa$x=a$, basi polynomials hizi zinajulikana kama Maclaurin polynomials kwa$f$. Sisi sasa kutoa ufafanuzi rasmi wa Taylor na Maclaurin polynomials kwa ajili ya kazi$f$.

Ufafanuzi$\PageIndex{2}$: Maclaurin polynomial

Kama$f$ ina$n$ derivatives katika$x=a$, basi$n^{\text{th}}$ -shahada Taylor polynomial ya$f$ saa$a$ ni

$$p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n. \nonumber$$

$n^{\text{th}}$-shahada Taylor polynomial kwa$f$ at$0$ inajulikana kama$n^{\text{th}}$ -shahada Maclaurin polynomial kwa$f$.

Sasa tunaonyesha jinsi ya kutumia ufafanuzi huu ili kupata polynomials kadhaa ya Taylor kwa$f(x)=\ln x$ saa$x=1$.

Mfano$\PageIndex{1}$: Finding Taylor Polynomials

Kupata Taylor polynomials$p_0,p_1,p_2$ na$p_3$ kwa$f(x)=\ln x$ saa$x=1$. Tumia matumizi ya graphing kulinganisha grafu ya$f$ na grafu ya$p_0,p_1,p_2$ na$p_3$.

Suluhisho

Ili kupata polynomials hizi Taylor, tunahitaji kutathmini$f$ na derivatives yake ya kwanza tatu katika$x=1$.

\ [kuanza {align*} f (x) &=\ ln x & f (1) &=0\\ [5pt] f (x) &=\
dfrac {1} {x} & f (1) &=1\\ [5pt]
f "(x) &=\\ dfrac {1} {x ^ 2} & f" (1) &=-1\\ [5pt]
f"' (x) &=\ dfrac {2} {x ^ 3} & f"' (1) &=2\ mwisho {align*}\]

Kwa hiyo,

$$\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}$$

Grafu ya$y=f(x)$ na ya kwanza Taylor polynomials tatu ni inavyoonekana katika Kielelezo$\PageIndex{1}$.

Kielelezo$\PageIndex{1}$: Kazi$y=\ln x$ na polynomials Taylor$p_0,p_1,p_2$ na$p_3$ katika$x=1$ ni walipanga juu ya grafu hii.

Zoezi$\PageIndex{1}$

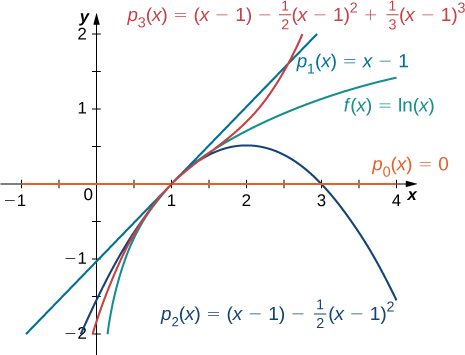
Kupata Taylor polynomials$p_0,p_1,p_2$ na$p_3$ kwa$f(x)=\dfrac{1}{x^2}$ saa$x=1$.

Kidokezo

Kupata kwanza derivatives tatu ya$f$ na kutathmini yao katika$x=1.$

Jibu

\ [kuanza {align*} p_0 (x) &=1\\ [5pt]
p_1 (x) &=1,1-2 (x-1)\\ [5pt]
p_2 (x) &=1,1-2 (x-1) +3 (x-1) ^2\\ [5pt]
p_3 (x) &=1,1-2 (x-1) +3 (x-1) +3 (x-1) -1) ^2,14 (x-1) ^3\ mwisho {align*}\]

Sasa tunaonyesha jinsi ya kupata Maclaurin polynomials kwa$e^x, \sin x,$ na$\cos x$. Kama ilivyoelezwa hapo juu, Maclaurin polynomials ni Taylor polynomials unaozingatia katika sifuri.

Mfano$\PageIndex{2}$: Finding Maclaurin Polynomials

Kwa kila moja ya kazi zifuatazo, tafuta formula kwa polynomials ya Maclaurin$p_0,p_1,p_2$ na$p_3$. Pata fomu ya$n^{\text{th}}$ shahada ya Maclaurin polynomial na uandike kwa kutumia alama ya sigma. Tumia matumizi ya graphing kulinganisha grafu ya$p_0,p_1,p_2$$p_3$ na kwa$f$.

1. $f(x)=e^x$
2. $f(x)=\sin x$
3. $f(x)=\cos x$

Suluhisho

Tangu$f(x)=e^x$, tunajua kwamba$f(x)=f′(x)=f''(x)=⋯=f^{(n)}(x)=e^x$ kwa integers zote chanya$n$. Kwa hiyo,

$$f(0)=f′(0)=f''(0)=⋯=f^{(n)}(0)=1 \nonumber$$

kwa integers wote chanya$n$. Kwa hiyo, tuna

\ (\ kuanza {align*} p_0 (x) &= f (0) =1,\\ [
5pt] p_1 (x) &f (0) +f (0) x=1+x,\\ [5pt]
p_2 (x) &= f (0) +f (0) x+\ dfrac {f "(0)} {2!} x^2=1+x+\ dfrac {1} {2} x ^ 2,\\ [5pt]
p_3 (x) &f (0) +f (0) x+\ dfrac {f "(0)} {2} x ^ 2+\ dfrac {f"' (0)} {3!} x^3=1+x+\ dfrac {1} {2} x^2+\ dfrac {1} {3!} x ^ 3,\ mwisho {align*}\)

\ (\ displaystyle\ kuanza {align*} p_n (x) &= f (0) +f (0) x+\ dfrac {f "(0)} {2} x ^ 2+\ dfrac {f"' (0)} {3!} x ^ 3++\ dfrac {f^ {(n)} (0)} {n!} x ^ n\\ [5pt]
&=1+x+\ dfrac {x ^ 2} {2!} +\ dfrac {x ^ 3} {3!} ++\ dfrac {x ^ n} {n!} \\ [5pt]
&=\ sum_ {k=0} ^n\ dfrac {x^k} {k!} \ mwisho {align*}\).

Kazi na polynomials tatu za kwanza za Maclaurin zinaonyeshwa kwenye Kielelezo$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$: Grafu inaonyesha kazi$y=e^x$ na Maclaurin polynomials$p_0,\,p_1,\,p_2$ na$p_3$.

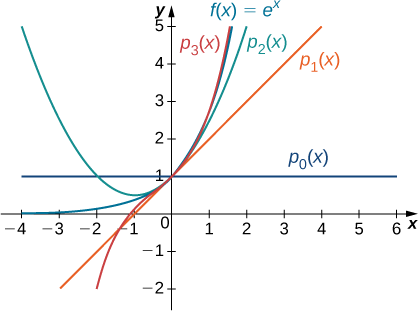
b Kwa$f(x)=\sin x$, maadili ya kazi na derivatives yake ya kwanza ya nne$x=0$ hutolewa kama ifuatavyo:

\ [kuanza {align*} f (x) &=\ dhambi x & f (0) &=0\\ [5pt]
f (x) &=\ cos x & f (0) &=1\\ [5pt]
f "(x) &=-\\ dhambi x & f" (0) &=0\\ [5pt]
f"' (x) &=\ x & f"' (0) &=-1\\ [5pt]
f^ {(4)} (x) &=\ dhambi x & f^ {(4)} (0) &=0. \ mwisho {align*}\]

Tangu derivative$\sin x,$ ya nne ni mfano kurudia. Hiyo ni,$f^{(2m)}(0)=0$ na$f^{(2m+1)}(0)=(−1)^m$ kwa$m≥0.$ hivyo, tuna

\ (\ kuanza {align*} p_0 (x) &=0,\\ [5pt]
p_1 (x) &=0+x=x,\\ [5pt]
p_2 (x) &=0+x+0=x,\\ [5pt]
p_3 (x) &=0+x+0-\ dfrac {1} {3!} x^3=x\ dfrac {x^3} {3!} ,\\ [5pt]
p_4 (x) &=0+x+0-\ dfrac {1} {3!} x^3+0=x\ dfrac {x^3} {3!} ,\\ [5pt]
p_5 (x) &=0+x+0-\ dfrac {1} {3!} x ^ 3+0+\ dfrac {1} {5!} x^5=x\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} ,\ mwisho {align*}\)

na kwa ajili ya$m≥0$,

\ [kuanza {align*} p_ {2m+1} (x) =p_ {2m+2} (x) &=x\ dfrac {x^3} {3!} +\ dfrac {x^5} {5!} -+ (-1) ^m\ dfrac {x^ {2m+1}} {(2m+1)!} \\ [5pt]
&=\ sum_ {k=0} ^m (-1) ^k\ dfrac {x^ {2k+1}} {(2k+1)!}. \ mwisho {align*}\]

Grafu ya kazi na polynomials yake Maclaurin ni inavyoonekana katika Kielelezo$\PageIndex{3}$.

Kielelezo$\PageIndex{3}$: Grafu inaonyesha kazi$y=\sin x$ na Maclaurin polynomials$p_1,\, p_3$ na$p_5$.

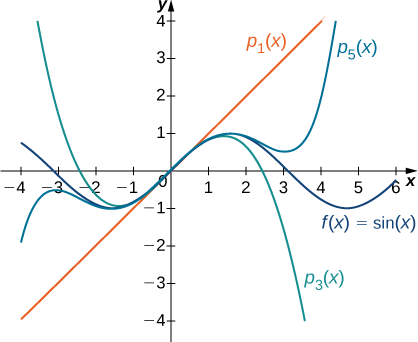
c Kwa$f(x)=\cos x$, maadili ya kazi na derivatives yake ya kwanza ya nne$x=0$ hutolewa kama ifuatavyo:

\ [kuanza {align*} f (x) &=\ cos x & f (0) &=1\\ [5pt]
f (x) &=-\ dhambi x & f (0) &=0\\ [5pt]
f "(x) &=\\ cos x & f" (0) &=-1\\ [5pt]
f"' (x) &=\\ dhambi x & f"' (0) &=0\\ [5pt]
f^ {(4)} (x) &=\ cos x & f^ {(4)} (0) &=1. \ mwisho {align*}\]

Tangu derivative ya nne ni$\sin x$, mfano unarudia. Kwa maneno mengine,$f^{(2m)}(0)=(−1)^m$ na$f^{(2m+1)}=0$ kwa$m≥0$. Kwa hiyo,

\ (\ kuanza {align*} p_0 (x) &=1,\\ [5pt]
p_1 (x) &=1+0=1,\\ [5pt]
p_2 (x) &=1+0-\ dfrac {1} {2!} x^2=1-\ dfrac {x^2} {2!} ,\\ [5pt]
p_3 (x) &=1+0\ dfrac {1} {2!} x^2+0=1\ dfrac {x^2} {2!} ,\\ [5pt]
p_4 (x) &=1+0\ dfrac {1} {2!} x ^ 2+0+\ dfrac {1} {4!} x^4=1-\ dfrac {x^2} {2!} +\ dfrac {x ^ 4} {4!} ,\\ [5pt]
p_5 (x) &=1+0\ dfrac {1} {2!} x ^ 2+0+\ dfrac {1} {4!} x^4+0=1\ dfrac {x^2} {2!} +\ dfrac {x ^ 4} {4!} ,\ mwisho {align*}\)

na kwa ajili ya$n≥0$,

\ [kuanza {align*} p_ {2m} (x) &=p_ {2m+1} (x)\\ [5pt]
&=1-\ dfrac {x^2} {2!} +\ dfrac {x ^ 4} {4!} -+ (-1) ^m\ dfrac {x^ {2m}} {(2m)!} \\ [5pt]
&=\ sum_ {k=0} ^m (-1) ^k\ dfrac {x^ {2k}} {(2k)!}. \ mwisho {align*}\]

Grafu ya kazi na polynomials Maclaurin kuonekana katika Kielelezo$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$: Kazi$y=\cos x$ na polynomials ya Maclaurin$p_0,p_2$ na$p_4$ hupangwa kwenye grafu hii.

Zoezi$\PageIndex{2}$

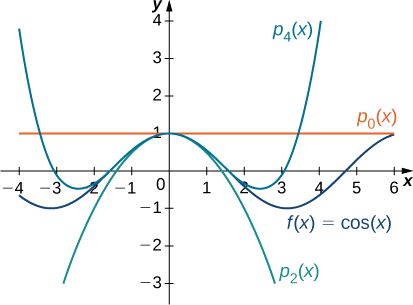
Kupata formula kwa ajili ya Maclaurin polynomials$p_0,\,p_1,\,p_2$ na$p_3$ kwa$f(x)=\dfrac{1}{1+x}$.

Pata formula ya$n^{\text{th}}$ shahada ya Maclaurin polynomial. Andika jibu lako kwa kutumia alama ya sigma.

Kidokezo

Kutathmini kwanza derivatives nne ya$f$ na kuangalia kwa mfano.

Jibu

$\displaystyle p_0(x)=1;\;p_1(x)=1−x;\;p_2(x)=1−x+x^2;\;p_3(x)=1−x+x^2−x^3;\;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=\sum_{k=0}^n(−1)^kx^k$

Theorem ya Taylor na Salio

Kumbuka kwamba$n^{\text{th}}$ -shahada Taylor polynomial kwa ajili ya kazi$f$ katika$a$ ni$n^{\text{th}}$ sehemu ya jumla ya Taylor mfululizo kwa$f$ saa$a$. Kwa hiyo, ili kuamua kama mfululizo wa Taylor unajiunga, tunahitaji kuamua kama mlolongo wa Taylor polynomials${p_n}$ hujiunga. Hata hivyo, si tu tunataka kujua kama mlolongo wa Taylor polynomials hujiunga, tunataka kujua kama hujiunga na$f$. Ili kujibu swali hili, tunafafanua salio$R_n(x)$ kama

$$R_n(x)=f(x)−p_n(x). \nonumber$$

Kwa mlolongo wa Taylor polynomials$f$ kuungana na, tunahitaji salio$R_n$ kuungana na sifuri. Kuamua ikiwa$R_n$ hujiunga na sifuri, tunaanzisha theorem ya Taylor na salio. Siyo tu theorem hii muhimu katika kuthibitisha kwamba mfululizo wa Taylor hujiunga na kazi yake inayohusiana, lakini pia itatuwezesha kupima jinsi$n^{\text{th}}$ shahada ya Taylor polynomial inavyofikia kazi.

Hapa sisi kuangalia kwa amefungwa juu ya$|R_n|.$ Fikiria kesi rahisi:$n=0$. Hebu$p_0$ 10 ^th Taylor polynomial saa$a$ kwa ajili ya kazi$f$. Salio$R_0$ linatimiza

$R_0(x)=f(x)−p_0(x)=f(x)−f(a).$

Ikiwa$f$ inatofautiana kwa muda$I$ unao$a$ na$x$, basi kwa Theorem ya Theorem ya Thamani ya Maana kuna idadi halisi$c$ kati$a$ na$x$ vile vile$f(x)−f(a)=f′(c)(x−a)$. Kwa hiyo,

$$R_0(x)=f′(c)(x−a). \nonumber$$

Kutumia Theorem ya Thamani ya Maana katika hoja sawa, tunaweza kuonyesha kwamba ikiwa$f$ ni$n$ mara kutofautishwa kwa muda$I$ unao$a$ na$x$, kisha$n^{\text{th}}$ salio$R_n$ hutimiza

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$

kwa baadhi ya idadi halisi$c$ kati ya$a$ na$x$. Ni muhimu kutambua kwamba thamani$c$ katika nambari hapo juu sio katikati$a$, bali ni thamani isiyojulikana$c$ kati$a$ na$x$. Fomula hii inaruhusu sisi kupata amefungwa juu ya salio$R_n$. Kama sisi kutokea kwa kujua kwamba$∣f^{(n+1)}(x)∣$ ni imepakana na baadhi ya idadi halisi$M$ juu ya kipindi hiki$I$, basi

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

kwa wote$x$ katika kipindi$I$.

Sisi sasa hali Theorem Taylor ya, ambayo inatoa uhusiano rasmi kati ya kazi$f$ na wake$n^{\text{th}}$ -shahada Taylor polynomial$p_n(x)$. Theorem hii inaruhusu sisi kufungwa makosa wakati wa kutumia Taylor polynomial takriban thamani kazi, na itakuwa muhimu katika kuthibitisha kwamba Taylor mfululizo kwa$f$ converges kwa$f$.

Theorem ya Taylor na Salio

Hebu$f$ kuwa kazi ambayo inaweza kutofautishwa$n+1$ mara juu ya muda$I$ zenye idadi halisi$a$. Hebu$p_n$ kuwa$n^{\text{th}}$ -shahada Taylor polynomial ya$f$ saa$a$ na basi

$$R_n(x)=f(x)−p_n(x) \nonumber$$

kuwa$n^{\text{th}}$ salio. Kisha kwa kila mmoja$x$ katika kipindi$I$, kuna idadi halisi$c$ kati$a$ na$x$ vile

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$ .

Ikiwa kuna idadi halisi$M$ kama hiyo$∣f^{(n+1)}(x)∣≤M$ kwa wote$x∈I$, basi

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

kwa ajili ya wote$x$ katika$I$.

Ushahidi

Kurekebisha uhakika$x∈I$ na kuanzisha kazi$g$ kama hiyo

$$g(t)=f(x)−f(t)−f′(t)(x−t)−\dfrac{f''(t)}{2!}(x−t)^2−⋯−\dfrac{f^{(n)}(t)}{n!}(x−t)^n−R_n(x)\dfrac{(x−t)^{n+1}}{(x−a)^{n+1}}. \nonumber$$

Tunadai kwamba$g$ inatimiza vigezo vya theorem ya Rolle. Kwa kuwa$g$ ni kazi ya polynomial (in$t$), ni kazi tofauti. Pia,$g$ ni sifuri katika$t=a$ na$t=x$ kwa sababu

$$\begin{align*} g(a) &=f(x)−f(a)−f′(a)(x−a)−\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n−R_n(x) \\[4pt] &=f(x)−p_n(x)−R_n(x) \\[4pt] &=0, \\[4pt] g(x) &=f(x)−f(x)−0−⋯−0 \\[4pt] &=0. \end{align*}$$

Kwa hiyo,$g$ satisfies Theorem Rolle ya, na kwa hiyo, kuna$c$ kati$a$ na$x$ vile kwamba$g′(c)=0.$ Sisi sasa mahesabu$g′$. Kutumia utawala wa bidhaa, tunaona kuwa

$$\dfrac{d}{dt}\left[\dfrac{f^{(n)}(t)}{n!}(x−t)^n\right]=−\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}+\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n. \nonumber$$

Kwa hiyo,

\ [kuanza {align} g( t) &=-f′ (t) + [f′ (t) -f "(t) (t) (x-t)] +\ kushoto [f" (t) (x-t) -\ dfrac {f"' (t)} {2!} (x-t) ^2\ haki] +\ nonumber\\
&\ quad+\ kushoto [\ dfrac {f^ {(n)} (t)} {(n)} {(n-1)!} (x-t) ^ {n -1} -\ dfrac {f^ {(n+1)} (t)} {n!} (x-t) ^n\ kulia] + (n+1) R_n (x)\ dfrac {(x-t) ^n} {(x-a) ^ {n+1}}\ mwisho {align}\ nonumber\].

Angalia kwamba kuna athari ya darubini. Kwa hiyo,

$$g'(t)=−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}} \nonumber$$ .

By theorem Rolle ya, sisi kuhitimisha kwamba kuna idadi$c$ kati ya$a$ na$x$ vile kwamba$g′(c)=0.$ Tangu

$$g′(c)=−\dfrac{f^{(n+1})(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}} \nonumber$$

tunahitimisha kwamba

$$−\dfrac{f^{(n+1)}(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}}=0. \nonumber$$

Kuongeza muda wa kwanza upande wa kushoto kwa pande zote mbili za equation na kugawanya pande zote mbili za equation na$n+1,$ tunahitimisha kwamba

$$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber$$

kama taka. Kutokana na ukweli huu, inafuata kwamba kama kuna$M$ vile kwamba$∣f^{(n+1)}(x)∣≤M$ kwa wote$x$ katika$I$, basi

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$ .

□

Si tu kwamba theorem Taylor ya kuruhusu sisi kuthibitisha kwamba Taylor mfululizo hujiunga na kazi, lakini pia inaruhusu sisi kukadiria usahihi wa Taylor polynomials katika makadirio ya maadili kazi. Tunaanza kwa kuangalia makadirio linear na quadratic ya$f(x)=\sqrt[3]{x}$ saa$x=8$ na kuamua jinsi sahihi makadirio haya ni katika kukadiria$\sqrt[3]{11}$.

Mfano$\PageIndex{3}$: Using Linear and Quadratic Approximations to Estimate Function Values

Fikiria kazi$f(x)=\sqrt[3]{x}$.

1. Kupata kwanza na ya pili Taylor polynomials kwa$f$ saa$x=8$. Tumia matumizi ya graphing kulinganisha polynomials hizi na$f$ karibu$x=8.$
2. Tumia polynomials hizi mbili kukadiria$\sqrt[3]{11}$.
3. Matumizi theorem Taylor ya kufungwa makosa.

Suluhisho:

a. kwa$f(x)=\sqrt[3]{x}$, maadili ya kazi na derivatives yake ya kwanza mbili katika$x=8$ ni kama ifuatavyo:

\ [kuanza {align*} f (x) &=\ sqrt [3] {x}, & f (8) &=2\\ [5pt] f (x) &=\
dfrac {1} {3x^ {2/3}}, & f (8) &=\ dfrac {1} {12}\ [5pt]
f "(x) &=\ dfrac {ї2} {9x^ {5/3}}, & f" (8) &=\ dfrac {1} {144.} \ mwisho {align*}\]

Hivyo, polynomials ya kwanza na ya pili ya Taylor katika$x=8$ hutolewa na

\ (\ kuanza {align*} p_1 (x) &f (8) +f (8) (x-8)\\ [5pt]
&=2+\ dfrac {1} {12} (x-8)\ mwisho {align*}\)

\ (\ kuanza {align*} p_2 (x) &= f (8) +f (8) (x-8) +\ dfrac {f "(8)} {2!} (x-8) ^2\\ [5pt]
&=2+\ dfrac {1} {12} (x-8) -\ dfrac {1} {288} (x-8) ^2. \ mwisho {align*}\)

Kazi na polynomials ya Taylor huonyeshwa kwenye Kielelezo$\PageIndex{5}$.

Kielelezo$\PageIndex{5}$: grafu ya$f(x)=\sqrt[3]{x}$ na makadirio linear na quadratic$p_1(x)$ na$p_2(x)$

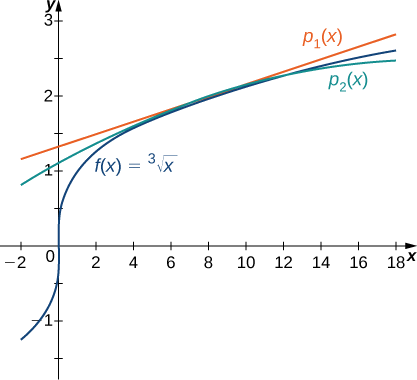
b Kutumia kwanza Taylor polynomial saa$x=8$, tunaweza kukadiria

$$\sqrt[3]{11}≈p_1(11)=2+\dfrac{1}{12}(11−8)=2.25. \nonumber$$

Kwa kutumia pili Taylor polynomial saa$x=8$, tunapata

$$\sqrt[3]{11}≈p_2(11)=2+\dfrac{1}{12}(11−8)−\dfrac{1}{288}(11−8)^2=2.21875. \nonumber$$

c Kwa Kumbuka, kuna c katika kipindi$(8,11)$ kama vile salio wakati$\sqrt[3]{11}$ inakadiriwa na polynomial ya kwanza ya Taylor inatimiza

$$R_1(11)=\dfrac{f''(c)}{2!}(11−8)^2. \nonumber$$

Hatujui thamani halisi ya$c,$ hivyo sisi kupata juu amefungwa juu$R_1(11)$ kwa kuamua thamani ya juu ya$f''$ juu ya muda$(8,11)$. Tangu$f''(x)=−\dfrac{2}{9x^{5/3}}$, thamani kubwa zaidi$|f''(x)|$ kwa muda huo hutokea$x=8$. Kwa kutumia ukweli kwamba$f''(8)=−\dfrac{1}{144}$, sisi kupata

$|R_1(11)|≤\dfrac{1}{144⋅2!}(11−8)^2=0.03125.$

Vile vile, kwa makisio$R_2(11)$, sisi kutumia ukweli kwamba

$R_2(11)=\dfrac{f'''(c)}{3!}(11−8)^3$.

Tangu$f'''(x)=\dfrac{10}{27x^{8/3}}$, thamani ya$f'''$ juu ya muda$(8,11)$ ni$f'''(8)≈0.0014468$. Kwa hiyo, tuna

$|R_2(11)|≤\dfrac{0.0011468}{3!}(11−8)^3≈0.0065104.$

Zoezi$\PageIndex{3}$:

Kupata kwanza na ya pili Taylor polynomials kwa$f(x)=\sqrt{x}$ saa$x=4$. Tumia polynomials hizi kukadiria$\sqrt{6}$. Matumizi theorem Taylor ya kufungwa makosa.

Kidokezo

Tathmini$f(4),f′(4),$ na$f''(4).$

Jibu

$p_1(x)=2+\dfrac{1}{4}(x−4);p_2(x)=2+\dfrac{1}{4}(x−4)−\dfrac{1}{64}(x−4)^2;p_1(6)=2.5;p_2(6)=2.4375;$

$|R_1(6)|≤0.0625;|R_2(6)|≤0.015625$

Mfano$\PageIndex{4}$: Approximating $\sin x$ Using Maclaurin Polynomials

Kutoka Mfano$\PageIndex{2b}$, polynomials ya Maclaurin$\sin x$ hutolewa na

$$p_{2m+1}(x)=p_{2m+2}(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−\dfrac{x^7}{7!}+⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!} \nonumber$$

kwa$m=0,1,2,….$

1. Matumizi ya tano Maclaurin polynomial$\sin x$ kwa takriban$\sin\left(\dfrac{π}{18}\right)$ na amefungwa makosa.
2. Kwa maadili$x$ gani ya tano Maclaurin polynomial$\sin x$ inakaribia ndani$0.0001$?

Suluhisho

a.

Maclaurin ya tano ya polynomial ni

$$p_5(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!} \nonumber$$ .

Kutumia polynomial hii, tunaweza kukadiria kama ifuatavyo:

$$\sin\left(\dfrac{π}{18}\right)≈p_5\left(\dfrac{π}{18}\right)=\dfrac{π}{18}−\dfrac{1}{3!}\left(\dfrac{π}{18}\right)^3+\dfrac{1}{5!}\left(\dfrac{π}{18}\right)^5≈0.173648. \nonumber$$

Ili kukadiria kosa, tumia ukweli kwamba Maclaurin ya sita ya polynomial ni$p_6(x)=p_5(x)$ na kuhesabu imefungwa$R_6(\dfrac{π}{18})$. Kwa Kumbuka, salio ni

$$R_6\left(\dfrac{π}{18}\right)=\dfrac{f^{(7)}(c)}{7!}\left(\dfrac{π}{18}\right)^7 \nonumber$$

kwa baadhi$c$ kati ya 0 na$\dfrac{π}{18}$. Kutumia ukweli kwamba$∣f^{(7)}(x)∣≤1$ kwa wote$x$, tunaona kwamba ukubwa wa kosa ni zaidi

$$\dfrac{1}{7!}⋅\left(\dfrac{π}{18}\right)^7≤9.8×10^{−10}. \nonumber$$

b.

Tunahitaji kupata maadili ya$x$ vile

$$\dfrac{1}{7!}|x|^7≤0.0001. \nonumber$$

Kutatua usawa huu kwa$x$, tuna kwamba tano Maclaurin polynomial inatoa makadirio ya ndani kwa muda mrefu$0.0001$ kama$|x|<0.907.$

Zoezi$\PageIndex{4}$

Matumizi ya nne Maclaurin polynomial$\cos x$ kwa takriban$\cos\left(\dfrac{π}{12}\right).$

Kidokezo

Maclaurin ya nne ya polynomial ni$p_4(x)=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}$.

Jibu

0.96593

Sasa kwa kuwa tuna uwezo wa kufungwa salio$R_n(x)$, tunaweza kutumia hii wajibu wa kuthibitisha kwamba Taylor mfululizo kwa$f$ saa converges kwa$f$.

Kuwakilisha Kazi na Taylor na Maclaurin Series

Sasa tunajadili masuala ya muunganiko kwa mfululizo wa Taylor. Tunaanza kwa kuonyesha jinsi ya kupata Taylor mfululizo kwa kazi, na jinsi ya kupata muda wake wa muunganiko.

Mfano$\PageIndex{5}$: Finding a Taylor Series

Kupata Taylor mfululizo kwa$f(x)=\dfrac{1}{x}$ saa$x=1$. Tambua muda wa kuunganishwa.

Suluhisho

Kwa maadili$f(x)=\dfrac{1}{x},$ ya kazi na derivatives yake ya kwanza ya nne$x=1$ ni

\ [kuanza {align*} f (x) &=\ dfrac {1} {x} & f (1) &=1\\ [5pt] f (x)
&=\dfrac {1} {x ^ 2} & f (1) &=-1\\ [5pt]
f "(x) &=\ dfrac {2} {x ^ 3} & f" (1) &=2! \\ [5pt]
f"' (x) &=\ dfrac {32} {x ^ 4} & f"' (1) &=—3! \\ [5pt]
f^ {(4)} (x) &=\ dfrac {432} {x ^ 5} & f^ {(4)} (1) &=4!. \ mwisho {align*}\]

Hiyo ni, tuna$f^{(n)}(1)=(−1)^nn!$ kwa wote$n≥0$. Kwa hiyo, mfululizo wa Taylor kwa$f$ saa$x=1$ hutolewa na

$\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(1)}{n!}(x−1)^n=\sum_{n=0}^∞(−1)^n(x−1)^n$.

Ili kupata muda wa kuunganisha, tunatumia mtihani wa uwiano. Tunaona kwamba

$\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{∣(−1)^{n+1}(x−1)n^{+1}∣}{|(−1)^n(x−1)^n|}=|x−1|$.

Hivyo, mfululizo hujiunga ikiwa$|x−1|<1.$ Hiyo ni, mfululizo hujiunga$0<x<2$. Kisha, tunahitaji kuangalia mwisho. Katika$x=2$, tunaona kwamba

$\displaystyle \sum_{n=0}^∞(−1)^n(2−1)^n=\sum_{n=0}^∞(−1)^n$

diverges na mtihani tofauti. Vile vile, katika$x=0,$

$\displaystyle \sum_{n=0}^∞(−1)^n(0−1)^n=\sum_{n=0}^∞(−1)^{2n}=\sum_{n=0}^∞1$

hutengana. Kwa hiyo, muda wa kuungana ni$(0,2)$.

Zoezi$\PageIndex{5}$

Kupata Taylor mfululizo kwa$f(x)=\dfrac{1}{2}$ saa$x=2$ na kuamua muda wake wa muunganiko.

Kidokezo

$f^{(n)}(2)=\dfrac{(−1)^nn!}{2^{n+1}}$

Jibu

$\dfrac{1}{2}\displaystyle \sum_{n=0}^∞\left(\dfrac{2−x}{2}\right)^n$. Muda wa kuungana ni$(0,4)$.

Tunajua kwamba mfululizo Taylor kupatikana katika mfano huu converges juu ya muda$(0,2)$, lakini jinsi gani sisi kujua ni kweli hujiunga na$f$? Tunazingatia swali hili kwa ujumla zaidi kwa muda, lakini kwa mfano huu, tunaweza kujibu swali hili kwa kuandika

$$f(x)=\dfrac{1}{x}=\dfrac{1}{1−(1−x)}. \nonumber$$

Hiyo ni,$f$ inaweza kuwakilishwa na mfululizo wa kijiometri$\displaystyle \sum_{n=0}^∞(1−x)^n$. Kwa kuwa hii ni mfululizo wa kijiometri, hujiunga kwa muda mrefu$\dfrac{1}{x}$ kama$|1−x|<1.$ Kwa hiyo, mfululizo wa Taylor unaopatikana katika Mfano$f(x)=\dfrac{1}{x}$ haujiunga$(0,2).$

Sasa tunaona swali zaidi ya jumla: kama Taylor mfululizo kwa kazi$f$ hujiunga katika baadhi ya muda, tunawezaje kuamua kama kweli hujiunga na$f$? Ili kujibu swali hili, kumbuka kwamba mfululizo hujiunga na thamani fulani ikiwa na tu ikiwa mlolongo wake wa kiasi cha sehemu hujiunga na thamani hiyo. Kutokana na mfululizo wa Taylor kwa$f$ saa$a$, jumla ya$n^{\text{th}}$ sehemu hutolewa na$n^{\text{th}}$ -shahada Taylor polynomial$p_n$. Kwa hiyo, ili kuamua kama mfululizo wa Taylor$f$ unajiunga na, tunahitaji kuamua kama

$\displaystyle \lim_{n→∞}p_n(x)=f(x)$.

Tangu salio$R_n(x)=f(x)−p_n(x)$, mfululizo wa Taylor hujiunga na$f$ ikiwa na tu

$\displaystyle \lim_{n→∞}R_n(x)=0.$

Sasa tunasema theorem hii rasmi.

Muungano wa Taylor mfululizo

Tuseme kwamba$f$ ina derivatives ya maagizo yote juu ya muda$I$ zenye$a$. Kisha mfululizo wa Taylor

$$\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n \nonumber$$

converges kwa$f(x)$ ajili ya wote$x$ katika$I$ kama na tu kama

$$\lim_{n→∞}R_n(x)=0 \nonumber$$

kwa ajili ya wote$x$ katika$I$.

Pamoja na theorem hii, tunaweza kuthibitisha kwamba Taylor mfululizo kwa$f$ saa converges na$f$ kama tunaweza kuthibitisha kwamba salio$R_n(x)→0$. Ili kuthibitisha kwamba$R_n(x)→0$, sisi kawaida kutumia amefungwa

$$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber$$

kutoka Theorem Taylor na salio.

Katika mfano unaofuata, tunapata mfululizo wa Maclaurin$e^x$$\sin x$ na kuonyesha kwamba mfululizo huu hujiunga na kazi zinazofanana kwa namba zote halisi kwa kuthibitisha kuwa mabaki$R_n(x)→0$ kwa namba zote halisi$x$.

Mfano$\PageIndex{6}$: Finding Maclaurin Series

Kwa kila moja ya kazi zifuatazo, tafuta mfululizo wa Maclaurin na muda wake wa kuungana. Tumia Kumbuka ili kuthibitisha kwamba mfululizo wa Maclaurin$f$ unajiunga na$f$ wakati huo.

1. $e^x$
2. $\sin x$

Suluhisho

a Kutumia$n^{\text{th}}$ shahada ya Maclaurin polynomial kwa$e^x$ kupatikana katika Mfano a., tunaona kwamba mfululizo wa Maclaurin$e^x$ hutolewa na

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$.

Kuamua muda wa kuunganisha, tunatumia mtihani wa uwiano. Tangu

$\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{|x|^{n+1}}{(n+1)!}⋅\dfrac{n!}{|x|^n}=\dfrac{|x|}{n+1}$,

tuna

$\displaystyle \lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=\lim_{n→∞}\dfrac{|x|}{n+1}=0$

kwa ajili ya wote$x$. Kwa hiyo, mfululizo hujiunga kabisa kwa wote$x$, na hivyo, muda wa kuungana ni$(−∞,∞)$. Ili kuonyesha kwamba mfululizo hujiunga na$e^x$ wote$x$, tunatumia ukweli kwamba$f^{(n)}(x)=e^x$ kwa wote$n≥0$ na$e^x$ ni kazi inayoongezeka$(−∞,∞)$. Kwa hiyo, kwa idadi yoyote halisi$b$, thamani ya juu$e^x$ ya wote$|x|≤b$ ni$e^b$. Hivyo,

$|R_n(x)|≤\dfrac{e^b}{(n+1)!}|x|^{n+1}$.

Tangu sisi tu ilionyesha kuwa

$\displaystyle \sum_{n=0}^∞\dfrac{|x|^n}{n!}$

converges kwa ajili ya wote$x$, na mtihani tofauti, tunajua kwamba

$\displaystyle \lim_{n→∞}\dfrac{|x|^{n+1}}{(n+1)!}=0$

kwa idadi yoyote halisi$x$. Kwa kuchanganya ukweli huu na theorem itapunguza, matokeo ni$\displaystyle \lim_{n→∞}R_n(x)=0.$

b Kutumia$n^{\text{th}}$ shahada ya Maclaurin polynomial$\sin x$ iliyopatikana katika Mfano b., tunaona kwamba mfululizo wa Maclaurin$\sin x$ hutolewa na

$\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}$.

Ili kutumia mtihani wa uwiano, fikiria

\ [kuanza {align*}\ dfrac {|a_ {n+1} |} {|a_n|} &=\ dfrac {|x|^ {2n+3}} {(2n+3)!} \ drac {(2n+1)!} {|x|^ {2n+1}}\ [5pt]
&=\ dfrac {|x|^2} {(2n+3) (2n+2)}\ mwisho {align*}. \ nambari isiyo\]

Tangu

$\displaystyle \lim_{n→∞}\dfrac{|x|^2}{(2n+3)(2n+2)}=0$

kwa ajili ya wote$x$, sisi kupata muda wa muunganiko kama$(−∞,∞).$ Kuonyesha kwamba mfululizo Maclaurin hujiunga na$\sin x$, angalia$R_n(x)$. Kwa kila$x$ kuna idadi halisi$c$ kati$0$ na$x$ vile kwamba

$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}$.

Tangu$∣f^{(n+1)}(c)∣≤1$ kwa integers wote$n$ na namba zote halisi $c$, tuna

$|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}$

kwa idadi yote halisi$x$. Kutumia wazo sawa na katika sehemu a., Matokeo ni$\displaystyle \lim_{n→∞}R_n(x)=0$ kwa wote$x$, na kwa hiyo, mfululizo wa Maclaurin kwa$\sin x$ hujiunga na$\sin x$ kwa kweli$x$.

Zoezi$\PageIndex{6}$

Kupata Maclaurin mfululizo kwa$f(x)=\cos x$. Tumia mtihani wa uwiano ili kuonyesha kwamba muda wa kuunganisha ni$(−∞,∞)$. Onyesha kwamba mfululizo wa Maclaurin hujiunga na$\cos x$ namba zote halisi$x$.

Kidokezo

Tumia polynomials ya Maclaurin$\cos x.$

Jibu

$\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{2n}}{(2n)!}$

Kwa mtihani wa uwiano, muda wa kuunganisha ni$(−∞,∞).$ Tangu$|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}$, mfululizo hujiunga na$\cos x$ kwa kweli$x$.

Kuthibitisha kwamba$e$ is Irrational

Katika mradi huu, sisi kutumia Polynomials Maclaurin kwa$e^x$ kuthibitisha kwamba$e$ ni irrational. Ushahidi unategemea kudhani kuwa$e$ ni busara na kufika kwa utata. Kwa hiyo, katika hatua zifuatazo, tunadhani$e=r/s$ kwa baadhi ya integers$r$ na$s$ wapi$s≠0.$

1. Andika polynomials ya Maclaurin$p_0(x),p_1(x),p_2(x),p_3(x),p_4(x)$ kwa$e^x$. Tathmini$p_0(1),p_1(1),p_2(1),p_3(1),p_4(1)$ ili kukadiria$e$.
2. Hebu$R_n(x)$ ueleze salio wakati unatumia$p_n(x)$ kukadiria$e^x$. Kwa hiyo,$R_n(x)=e^x−p_n(x)$, na$R_n(1)=e−p_n(1)$. Kutokana kwamba$e=\dfrac{r}{s}$ kwa integers$r$ na$s$, kutathmini$R_0(1),R_1(1),R_2(1),R_3(1),R_4(1).$
3. Kutumia matokeo kutoka sehemu ya 2, onyesha kwamba kwa kila salio$R_0(1),R_1(1),R_2(1),R_3(1),R_4(1),$ tunaweza kupata integer$k$ kama hiyo$kR_n(1)$ ni integer kwa$n=0,1,2,3,4.$
4. Andika formula kwa$n^{\text{th}}$ -shahada Maclaurin polynomial$p_n(x)$ kwa$e^x$ na sambamba salio$R_n(x).$ Onyesha kwamba$sn!R_n(1)$ ni integer.
5. Matumizi theorem Taylor ya kuandika formula wazi kwa$R_n(1)$. Kuhitimisha kwamba$R_n(1)≠0$, na kwa hiyo,$sn!R_n(1)≠0$.
6. Tumia theorem ya Taylor ili kupata makadirio ya$R_n(1)$. Tumia makadirio haya pamoja na matokeo kutoka sehemu ya 5 ili kuonyesha hilo$|sn!R_n(1)|<\dfrac{se}{n+1}$. Kuhitimisha kwamba ikiwa$n$ ni kubwa ya kutosha, basi$|sn!R_n(1)|<1$. Kwa hiyo,$sn!R_n(1)$ ni integer na ukubwa chini ya 1. Hivyo,$sn!R_n(1)=0$. Lakini kutoka sehemu ya 5, tunajua hilo$sn!R_n(1)≠0$. Tumefika kwa utata, na kwa hiyo, dhana ya awali kwamba e ni busara lazima iwe uongo.

Dhana muhimu

• Taylor polynomials hutumiwa takriban kazi karibu na thamani$x=a$. Maclaurin polynomials ni Taylor polynomials katika$x=0$.
• $n^{\text{th}}$-shahada Taylor polynomials kwa ajili ya kazi$f$ ni kiasi sehemu ya Taylor mfululizo kwa$f$.
• Ikiwa kazi$f$ ina uwakilishi wa mfululizo wa nguvu$x=a$, basi hutolewa na mfululizo wake wa Taylor$x=a$.
• mfululizo Taylor kwa$f$ converges na$f$ kama na tu kama$\displaystyle \lim_{n→∞}R_n(x)=0$ wapi$R_n(x)=f(x)−p_n(x)$.
• Taylor mfululizo kwa$e^x, \sin x$,$\cos x$ na kuungana na kazi husika kwa kila x halisi.

Mlinganyo muhimu

• Taylor mfululizo kwa ajili ya kazi katika$f$ hatua$x=a$

$\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯$

faharasa

Maclaurin polynomial

a Taylor polynomial katikati katika$0$;$n^{\text{th}}$ -shahada Taylor polynomial kwa$f$ saa$0$ ni$n^{\text{th}}$ -shahada Maclaurin polynomial kwa$f$

Maclaurin mfululizo

Taylor mfululizo kwa ajili ya kazi$f$ katika$x=0$ inajulikana kama Maclaurin mfululizo kwa$f$

Taylor polynomials

$n^{\text{th}}$shahada ya Taylor polynomial kwa$f$ saa$x=a$ ni$p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n$

Taylor mfululizo

mfululizo nguvu kwa$a$ kuwa hujiunga na kazi katika baadhi$f$ ya muda wazi zenye$a$.

Theorem ya Taylor na salio

kwa ajili ya kazi$f$ na$n^{\text{th}}$ -shahada Taylor polynomial kwa$f$ saa$x=a$, salio$R_n(x)=f(x)−p_n(x)$ satisfies$R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1}$

kwa baadhi$c$ kati$x$ na$a$; ikiwa kuna muda$I$ unao$a$ na idadi halisi$M$ kama hiyo$∣f^{(n+1)}(x)∣≤M$$x$ kwa wote$I$, basi$|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1}$