9.5E: Mazoezi ya Sehemu ya 9.5

Katika mazoezi ya 1 - 30, sema kama kila mfululizo wafuatayo hujiunga kabisa, kwa hali ya kimwili, au sio kabisa.

1)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}\)

2)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}\)

Jibu

Mfululizo huu unatofautiana na mtihani wa tofauti. Masharti si huwa na sifuri.

3)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}\)

4)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}\)

Jibu

Inabadilisha hali kwa njia ya kupima mfululizo, tangu\(\sqrt{n+3}/n\) inapungua na kikomo chake ni 0. Haiunganishi kabisa kwa kulinganisha na\(p\) -mfululizo,\(p=1/2\).

5)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}\)

6)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}\)

Jibu

Inajiunga kabisa na kikomo kulinganisha na\(3^n/4^n,\) kwa mfano.

7)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n\)

8)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n\)

Jibu

Inapingana na mtihani tofauti tangu\(\displaystyle \lim_{n→∞}|a_n|=e\) na si\(0\).

9)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2n\)

10)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2n\)

Jibu

Inapotofautiana na mtihani wa kutofautiana, kwani maneno yake hayakuwa na sifuri. Kikomo cha mlolongo wa masharti yake haipo.

11)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2(1/n)\)

12)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2(1/n)\)

Jibu

\(\displaystyle \lim_{n→∞}\cos^2(1/n)=1.\)Diverges na mtihani tofauti.

13)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1/n)\)

14)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})\)

Jibu

Converges na alternating mfululizo mtihani.

15)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}\)

16)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}\)

Jibu

Inajiunga kwa hali kwa kubadilisha mtihani wa mfululizo. Je, si hukutana kabisa na kikomo kulinganisha na\(p\) -mfululizo,\(p=π−e\)

Suluhisho:

17)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}\)

18)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}\)

Jibu

Diverges; maneno si huwa na sifuri.

19)\(\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})\) (kidokezo:\(n^{1/n}≈1+\ln(n)/n\) kwa kubwa\(n\).)

20)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)\) (kidokezo:\(\cos(1/n)≈1−1/n^2\) kwa kubwa\(n\).)

Jibu

Converges na alternating mfululizo mtihani. Haina hujiunga kabisa na kikomo kulinganisha na mfululizo harmonic.

21)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})\) (Kidokezo: Rationalize nambari.)

22)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)\) (Kidokezo: Msalaba kuzidisha kisha rationalize nambari.)

Jibu

Inajiunga kabisa na kikomo kulinganisha na\(p\) -mfululizo\(p=3/2\),, baada ya kutumia ladha.

23)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)\)

24)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)\) (Dokezo: Tumia Theorem ya Thamani ya Maana.)

Jibu

Converges na alternating mfululizo mtihani tangu\( n(\tan^{−1}(n+1)−\tan^{−1}n)\) ni kupungua kwa sifuri kwa kubwa\(n\) .Je, si hujiunga kabisa na kikomo kulinganisha na mfululizo harmonic baada ya kutumia ladha.

25)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)\)

26)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)\)

Jibu

Inajiunga kabisa, tangu\( a_n=\dfrac{1}{n}−\dfrac{1}{n+1}\) ni suala la mfululizo wa telescoping.

27)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n}\)

28)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n^{1/n}}\)

Jibu

Masharti si huwa na sifuri. Mfululizo hutofautiana na mtihani wa tofauti.

29)\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\sin(\frac{nπ}{2})\)

30)\(\displaystyle \sum^∞_{n=1}\sin(nπ/2)\sin(1/n)\)

Jibu

Converges na alternating mfululizo mtihani. Haina hujiunga kabisa na kikomo kulinganisha na mfululizo harmonic.

Katika mazoezi ya 31 - 36, tumia makadirio ya\(|R_N|≤b_{N+1}\) kupata thamani ya\(N\) hiyo inathibitisha kwamba jumla ya\(N\) masharti ya kwanza ya mfululizo wa kubadilisha\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) hutofautiana na jumla isiyo na kipimo na kosa kubwa lililopewa. Tumia jumla ya sehemu\(S_N\) kwa hili\(N\).

31) [T]\(b_n=1/n,\) kosa\( <10^{−5}\)

32) [T]\(b_n=1/\ln(n), n≥2,\) kosa\(<10^{−1}\)

Jibu

\( \ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…\)

33) [T]\(b_n=1/\sqrt{n},\) kosa\(<10^{−3}\)

34) [T]\(b_n=1/2^n\), kosa\(<10^{−6}\)

Jibu

\(2^{N+1}>10^6\)\(N+1>6\ln(10)/\ln(2)=19.93.\)au\(N≥19; S_{19}=0.333333969…\)

35) [T]\(b_n=ln(1+\dfrac{1}{n}),\) kosa\( <10^{−3}\)

36) [T]\(b_n=1/n^2,\) kosa\(<10^{−6}\)

Jibu

\((N+1)^2>10^6\)au\(N>999; S_{1000}≈0.822466.\)

Kwa mazoezi 37 - 45, onyesha kama kila moja ya kauli zifuatazo ni kweli au ya uongo. Ikiwa taarifa hiyo ni ya uongo, fanya mfano ambao ni uongo.

37) Ikiwa\( b_n≥0\) inapungua na\(\displaystyle \lim_{n→∞}b_n=0\), basi\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) hujiunga kabisa.

38) Ikiwa\( b_n≥0\) inapungua, basi\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) hujiunga kabisa.

Jibu

Kweli. \(b_n\)haja huwa na sifuri tangu kama\(\displaystyle c_n=b_n−\lim b_n\), basi\(c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.\)

39) Ikiwa\( b_n≥0\) na\(\displaystyle \lim_{n→∞}b_n=0\) kisha\(\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})\) hujiunga.

40) Ikiwa\(b_n≥0\) inapungua na\(\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})\) hujiunga kisha\(\displaystyle \sum_{n=1}^∞b_{3n−2}\) hujiunga.

Jibu

Kweli. \(b_{3n−1}−b_{3n}≥0,\)hivyo muunganiko wa\(\displaystyle \sum b_{3n−2}\) ifuatavyo kutoka mtihani kulinganisha.

41) Ikiwa\(b_n≥0\) inapungua na\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) hujiunga na hali ya kimwili lakini sio kabisa, basi\(b_n\) haipatikani na sifuri.

42) Hebu\(a^+_n=a_n\) kama\(a_n≥0\) na\( a^−_n=−a_n\) kama\(a_n<0\). (Pia,\( a^+_n=0\) kama\(a_n<0\) na\(a^−_n=0\) kama\(a_n≥0\).) Ikiwa\(\displaystyle \sum_{n=1}^∞a_n\) hujiunga na hali ya kimwili lakini si kabisa, basi\(\displaystyle \sum_{n=1}^∞a^+_n\) wala\(\displaystyle \sum_{n=1}^∞a^−_n\) usiingie.

Jibu

Kweli. Ikiwa mtu hujiunga, basi ni lazima mwingine, akimaanisha kuunganishwa kabisa.

43) Tuseme kwamba\(a_n\) ni mlolongo wa idadi chanya halisi na kwamba\(\displaystyle \sum_{n=1}^∞a_n\) converges.

44) Tuseme kwamba\(b_n\) ni mlolongo wa kiholela wa wale na wachache. Je,\(\displaystyle \sum_{n=1}^∞a_nb_n\) lazima hujiunga?

45) Tuseme kwamba\(a_n\) ni mlolongo kama kwamba\(\displaystyle \sum_{n=1}^∞a_nb_n\) hujiunga kwa kila mlolongo iwezekanavyo\(b_n\) wa zero na wale. Je,\(\displaystyle \sum_{n=1}^∞a_n\) hujiunga kabisa?

Jibu

Ndiyo. Kuchukua\(b_n=1\) kama\(a_n≥0\) na\( b_n=0\) kama\(a_n<0\). Kisha\(\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:a_n≥0}a_n\) hujiunga. Vile vile, mtu anaweza kuonyesha\(\displaystyle \sum_{n:a_n<0}a_n\) converges. Kwa kuwa mfululizo wote hujiunga, mfululizo lazima uunganishe kabisa.

Katika mazoezi 46 - 49, mfululizo haukukidhi nadharia za mtihani wa mfululizo wa mfululizo kama ilivyoelezwa. Katika kila kesi, hali ambayo hypothesis si kuridhika. Hali kama mfululizo hujiunga kabisa.

46)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\sin^2n}{n}\)

47)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\cos^2n}{n}\)

Jibu

Si kupungua. Haiunganishi kabisa.

48)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯\)

49)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯\)

Jibu

Si mbadala. Inaweza kuelezwa kama\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),\) ambayo inatofautiana kwa kulinganisha na\(\displaystyle \sum_{n=1}^∞\frac{1}{3n−2}.\)

50) Onyesha kwamba mfululizo wa kubadilisha\(\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+⋯\) hauunganishi. Nini hypothesis ya mtihani wa mfululizo wa mfululizo haukufikiwa?

51) Tuseme kwamba\(\displaystyle \sum a_n\) hujiunga kabisa. Onyesha kwamba mfululizo unao na maneno mazuri\(a_n\) pia hujiunga.

Jibu

Hebu\(a^+_n=a_n\) kama\(a_n≥0\) na\(a^+_n=0\) kama\( a_n<0\). Kisha\(a^+_n≤|a_n|\) kwa ajili ya wote\(n\) hivyo mlolongo wa kiasi sehemu ya\( a^+_n\) ni kuongezeka na imepakana juu na mlolongo wa kiasi sehemu ya\( |a_n|\), ambayo hujiunga; hivyo,\(\displaystyle \sum_{n=1}^∞a^+_n\) hujiunga.

52) Onyesha kwamba mfululizo wa kubadilisha\(\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯\) hauunganishi. Nini hypothesis ya mtihani wa mfululizo wa mfululizo haukufikiwa?

53) Fomula\(\displaystyle \cos θ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯\) itatokana katika sura inayofuata. Tumia salio\(|R_N|≤b_{N+1}\) ili kupata amefungwa kwa kosa katika kukadiria\(\cos θ\) kwa jumla ya sehemu ya tano\(1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!\) kwa\(θ=1, θ=π/6,\) na\(θ=π.\)

Jibu

Kwa\(N=5\) moja ina\(∣R_N∣b_6=θ^{10}/10!\). Wakati\(θ=1, R_5≤1/10!≈2.75×10^{−7}\). Wakati\(θ=π/6,\)\(R_5≤(π/6)^{10}/10!≈4.26×10^{−10}\). Wakati\(θ=π, R_5≤π^{10}/10!=0.0258.\)

54) Fomula\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) itatokana katika sura inayofuata. Tumia salio\(|R_N|≤b_{N+1}\) ili kupata amefungwa kwa kosa katika kukadiria\(\sin θ\) kwa jumla ya sehemu ya tano\(θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!\) kwa\(θ=1, θ=π/6,\) na\(θ=π.\)

55) Ni maneno ngapi\(\cos θ=1−\dfrac{θ^2}{2!}+\dfrac{θ^4}{4!}−\dfrac{θ^6}{6!}+⋯\) yanahitajika ili takriban\(\cos 1\) sahihi kwa hitilafu ya zaidi\( 0.00001\)?

Jibu

Basi\( b_n=1/(2n−2)!.\) basi\(R_N≤1/(2N)!<0.00001\) wakati\((2N)!>10^5\) au\(N=5\) na\(\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…\), wakati\(\cos 1=0.5403023…\)

56) Ni maneno ngapi\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) yanahitajika ili takriban\(\sin 1\) sahihi kwa hitilafu ya zaidi\(0.00001?\)

57) Wakati mwingine mfululizo wa\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) kubadilisha hujiunga na sehemu fulani ya mfululizo wa kubadilisha kabisa kwa\(\displaystyle \sum_{n=1}^∞b_n\) kiwango cha kasi. Kutokana na kwamba\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}\), tafuta\(\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯\). Ni ipi kati ya mfululizo\(\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}\) na\(\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}\) inatoa makadirio bora ya\(π^2\) kutumia\(1000\) maneno?

Jibu

Basi\(\displaystyle T=\sum\frac{1}{n^2}.\) basi\(T−S=\dfrac{1}{2}T\), hivyo\(S=T/2\). \(\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….\)Mfululizo wa kubadilisha ni sahihi zaidi kwa\(1000\) maneno.

mfululizo alternating katika mazoezi 58 & 59 hujiunga na wingi kupewa ya\(π\). Pata thamani ya\(N\) kutabiriwa na makadirio yaliyobaki kama kwamba jumla ya\(N^{\text{th}}\) sehemu ya mfululizo inakaribia kwa usahihi upande wa kushoto ndani ya kosa lililopewa. Pata kiwango cha chini\(N\) ambacho kosa lililofungwa linashikilia, na upe thamani ya takriban inayohitajika katika kila kesi. Hadi\(15\) decimals maeneo,\( π=3.141592653589793….\)

58) [T]\(\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},\) kosa\(<0.0001\)

59) [T]\(\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},\) kosa\(<0.0001\)

Jibu

\(N=6, S_N=0.9068\)

60) [T] Mfululizo\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) una jukumu muhimu katika usindikaji wa ishara. Onyesha kwamba\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) hujiunga wakati wowote\(0<x<π\). (Kidokezo: Tumia formula kwa sine ya jumla ya pembe.)

61) [T] Kama ni\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,\) nini\(\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?\)

Jibu

\(\ln(2).\)Jumla ya\(n^{\text{th}}\) sehemu ni sawa na ile ya mfululizo wa harmonic mbadala.

62) [T] Plot mfululizo\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) kwa\(0≤x<1\). Eleza kwa nini\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) hutofautiana wakati\(x=0,1\). Je, mfululizo hufanyaje kwa wengine\(x\)?

63) [T] Plot mfululizo\(\displaystyle \sum_{n=1}^{100}\frac{\sin(2πnx)}{n}\) kwa\(0≤x<1\) na maoni juu ya tabia yake

Jibu

Mfululizo unaruka haraka karibu na mwisho. Kwa\(x\) mbali na mwisho, grafu inaonekana kama\( π(1/2−x)\).

64) [T] Plot mfululizo\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n^2}\) kwa\( 0≤x<1\) na kuelezea grafu yake.

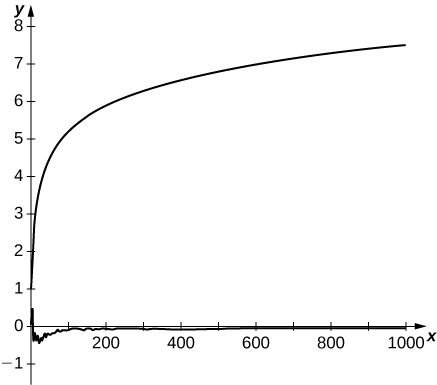
65) [T] Mfululizo wa harmonic unabadilisha hujiunga kwa sababu ya kufuta kati ya masharti yake. Jumla yake inajulikana kwa sababu kufuta kunaweza kuelezewa wazi. random harmonic mfululizo ni moja ya fomu\(\displaystyle \sum_{n=1}^∞\frac{S_n}{n}\), ambapo\(s_n\) ni nasibu yanayotokana mlolongo wa\(±1's\) ambayo maadili\(±1\) ni sawa uwezekano wa kutokea. Matumizi random jenereta ya simu ya kuzalisha\(1000\) random\(±1's\) na njama kiasi sehemu\(\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}\) ya random harmonic mlolongo wako\(N=1\) kwa\(1000\). Linganisha na njama ya kiasi cha kwanza cha\(1000\) sehemu ya mfululizo wa harmonic.

Jibu

Hapa ni matokeo ya kawaida. Curve ya juu ina kiasi cha sehemu ya mfululizo wa harmonic. Curve chini viwanja kiasi sehemu ya mfululizo random harmonic.

66) [T] Makadirio ya\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) yanaweza kuharakishwa kwa kuandika kiasi chake cha sehemu kama\(\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}\) na kukumbuka kwamba\(\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}\) hujiunga na moja kama\( N→∞.\) Linganisha makadirio ya\(π^2/6\) kutumia kiasi\(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}\) na makadirio ya kutumia\(\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}\).

67) [T] Euler kubadilisha kuandika upya\(\displaystyle S=\sum_{n=0}^∞(−1)^nb_n\) kama\(\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}\). Kwa mfululizo wa harmonic mbadala, inachukua fomu\(\displaystyle \ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}\). Compute kiasi sehemu ya\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) mpaka takriban\(\ln(2)\) sahihi na ndani ya\(0.0001\). Ni maneno ngapi yanahitajika? Linganisha jibu hili kwa idadi ya masharti ya mfululizo wa harmonic unaohitajika ili kukadiria\(\ln(2)\).

Jibu

Kwa mtihani wa mfululizo wa mfululizo,\(|S_n−S|≤b_{n+1},\) hivyo mtu anahitaji\(10^4\) masharti ya mfululizo wa harmonic unaobadilisha\(\ln(2)\) ili kukadiria ndani\(0.0001\). Kiasi cha kwanza\(10\) cha mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) ni (hadi decimals nne)\( 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931\) na jumla ya sehemu ya kumi ni ndani\(0.0001\) ya\(\ln(2)=0.6931….\)

68) [T] Katika maandiko imesemwa kuwa mfululizo wa hali ya kawaida unaweza kupangwa upya ili kugeuza na namba yoyote. Hapa ni rahisi kidogo, lakini sawa, ukweli. Kama\(a_n≥0\) ni kwamba\(a_n→0\) kama\(n→∞\) lakini\(\displaystyle \sum_{n=1}^∞a_n\) diverges, basi, kutokana na idadi yoyote\(A\) kuna mlolongo\(s_n\) wa\( ±1's\) vile kwamba\(\displaystyle \sum_{n=1}^∞a_ns_n→A.\) Onyesha hii kwa\(A>0\) kama ifuatavyo.

a. recursively kufafanua\(s_n\) na\( s_n=1\) kama\(\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A\) na\( s_n=−1\) vinginevyo.

b Eleza kwa nini hatimaye\(S_n≥A,\) na kwa yoyote\(m\) kubwa kuliko hii\(n\),\(A−a_m≤S_m≤A+a_m\).

c Eleza kwa nini hii ina maana kwamba\( S_n→A\) kama\( n→∞.\)