9.5: Mfululizo Mbadala
- Page ID
- 178878
- Tumia mtihani wa mfululizo wa mfululizo ili kupima mfululizo wa kubadilisha kwa kuunganisha.
- Tathmini jumla ya mfululizo wa kubadilisha.
- Eleza maana ya kuunganishwa kabisa na ushirikiano wa masharti.
Hadi sasa katika sura hii, sisi kimsingi kujadiliwa mfululizo na maneno chanya. Katika sehemu hii sisi kuanzisha mfululizo alternating- wale mfululizo ambao maneno mbadala katika ishara. Tutaonyesha katika sura ya baadaye kwamba mfululizo huu mara nyingi hutokea wakati wa kusoma mfululizo wa nguvu. Baada ya kufafanua mfululizo wa kubadilisha, tunaanzisha mtihani wa mfululizo wa kubadilisha ili kuamua kama mfululizo huo unajiunga.
Mtihani wa Mfululizo Mbadala
Mfululizo ambao maneno yake yanatofautiana kati ya maadili mazuri na hasi ni mfululizo wa kubadilisha. Kwa mfano, mfululizo
\[\sum_{n=1}^∞ \left(−\dfrac{1}{2} \right)^n=−\dfrac{1}{2}+\dfrac{1}{4}−\dfrac{1}{8}+\dfrac{1}{16}− \ldots \label{eq1} \]
na
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots \label{eq2} \]
wote ni mfululizo alternating.
Mfululizo wowote ambao maneno yake yanatofautiana kati ya maadili mazuri na hasi huitwa mfululizo wa kubadilisha. Mfululizo mbadala unaweza kuandikwa kwa fomu
\[\sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+ \ldots \label{eq3} \]
au
\[\sum_{n−1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−\ldots \label{eq4} \]
Ambapo\( b_n≥0\) kwa integers zote nzuri\(n\).
Mfululizo (1), umeonyeshwa katika Equation\ ref {eq1}, ni mfululizo wa kijiometri. Tangu\( |r|=|−1/2|<1,\) mfululizo hujiunga. Mfululizo (2), umeonyeshwa katika Equation\ ref {eq2}, inaitwa mfululizo wa harmonic mbadala. Tutaonyesha kwamba wakati mfululizo wa harmonic unajitokeza, mfululizo wa harmonic unaogeuka. Ili kuthibitisha hili, tunaangalia mlolongo wa kiasi cha sehemu\( \{S_k\}\) (Kielelezo 1).
Fikiria maneno isiyo ya kawaida\( S_{2k+1}\) kwa\( k≥0\). Tangu\( 1/(2k+1)<1/2k,\)
\[S_{2k+1}=S_{2k−1}−\dfrac{1}{2k}+\dfrac{1}{2k+1}<S_{2k−1}. \nonumber \]
Kwa hiyo,\( \{S_{2k+1}\}\) ni mlolongo kupungua. Pia,
\[S_{2k+1}=\left(1−\dfrac{1}{2}\right)+\left(\dfrac{1}{3}−\dfrac{1}{4}\right)+ \ldots + \left(\dfrac{1}{2k−1}−\dfrac{1}{2k}\right)+\dfrac{1}{2k+1}>0. \nonumber \]
Kwa hiyo,\( \{S_{2k+1}\}\) imepakana chini. Kwa kuwa\( \{S_{2k+1}\}\) ni kupungua mlolongo kwamba imepakana chini, na Monotone\( \{S_{2k+1}\}\) Convergence Theorem, hujiunga. Vile vile, hata maneno\( \{S_{2k}\}\) huunda mlolongo unaoongezeka ambao umepakana hapo juu kwa sababu
\[S_{2k}=S_{2k−2}+\dfrac{1}{2k−1}−\dfrac{1}{2k}>S_{2k−2} \nonumber \]
na
\[S_{2k}=1+ \left(−\dfrac{1}{2}+\dfrac{1}{3}\right)+\ldots + \left(−\dfrac{1}{2k−2}+\dfrac{1}{2k−1}\right)−\dfrac{1}{2k}<1. \nonumber \]
Kwa hiyo, kwa Theorem ya Monotone Convergence, mlolongo\( \{S_{2k}\}\) pia hujiunga. Tangu
\[S_{2k+1}=S_{2k}+\dfrac{1}{2k+1}, \nonumber \]
tunajua kwamba
\[\lim_{k→∞}S_{2k+1}=\lim_{k→∞}S_{2k}+\lim_{k→∞}\dfrac{1}{2k+1}. \nonumber \]
Kuruhusu\(\displaystyle S=\lim_{k→∞}S_{2k+1}\) na kutumia ukweli kwamba\( 1/(2k+1)→0,\) tunahitimisha hilo\(\displaystyle \lim_{k→∞}S_{2k}=S\). Kwa kuwa maneno isiyo ya kawaida na masharti hata katika mlolongo wa kiasi cha sehemu hujiunga na kikomo sawa\( S\), inaweza kuonyeshwa kuwa mlolongo wa kiasi cha sehemu hujiunga na\( S\), na kwa hiyo mfululizo wa harmonic unabadilisha\( S\).
Inaweza pia kuonyeshwa kuwa\( S=\ln 2,\) na tunaweza kuandika
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+a\ldots=\ln (2). \nonumber \]
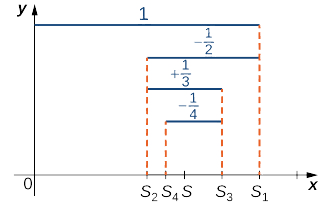
□
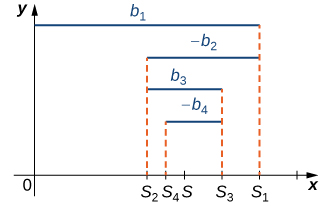
Kwa ujumla, mfululizo wowote wa fomu (3) (Equation\ ref {eq3}) au (4) (Equation\ ref {eq4}) hujiunga kwa muda mrefu kama\( b_1≥b_2≥b_3≥⋯\) na\( b_n→0\) (Kielelezo 2). Ushahidi huo ni sawa na ushahidi wa mfululizo wa harmonic mbadala.
Mfululizo mbadala wa fomu
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]au\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
hukutana kama
- \( 0≤b_{n+1}≤b_n\)kwa wote\( n≥1\) na
- \(\displaystyle \lim_{n→∞}b_n=0.\)
Hii inajulikana kama mtihani wa mfululizo wa kubadilisha.
Tunasema kwamba theorem hii ni kweli zaidi kwa ujumla kwa muda mrefu kama kuna baadhi integer\( N\) kama kwamba\( 0≤b_{n+1}≤b_n\) kwa wote\( n≥N.\)
Kwa kila moja ya mfululizo wafuatayo, onyesha kama mfululizo unajiunga au hupungua.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n^2}\)
- \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+1}\)
Suluhisho
a. tangu\( \dfrac{1}{(n+1)^2}<\dfrac{1}{n^2}\) na mfululizo\( \dfrac{1}{n^2}→0,\) hujiunga.
b. tangu\( n/(n+1)↛0\) kama\( n→∞\), hatuwezi kutumia alternating mfululizo mtihani. Badala yake, tunatumia mtihani wa neno la nth kwa tofauti. Tangu\(\displaystyle \lim_{n→∞}\dfrac{n}{n+1}=1≠0,\) mfululizo hupungua.
Kuamua kama mfululizo\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2^n}\) hujiunga au hupungua.
- Kidokezo
-
Ni\( \left\{\frac{n}{2^n}\right\}\) kupungua? Ni nini\(\displaystyle \lim_{n→∞}\frac{n}{2^n}\)?
- Jibu
-
Mfululizo hujiunga.
Salio ya Mfululizo Mbadala
Ni vigumu kwa uwazi mahesabu ya jumla ya mfululizo wengi alternating, hivyo kawaida jumla ni takriban kwa kutumia jumla ya sehemu. Wakati wa kufanya hivyo, sisi ni nia ya kiasi cha makosa katika makadirio yetu. Fikiria mfululizo mbadala
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]
kuridhisha mawazo ya mtihani wa mfululizo wa kubadilisha. Hebu\( S\) ueleze jumla ya mfululizo huu na\( {S_k}\) uwe mlolongo unaofanana wa kiasi cha sehemu. Kutoka Kielelezo\( \PageIndex{2}\), tunaona kwamba kwa integer yoyote\( N≥1\), salio\( R_N\) satisfies
\[|R_N|=|S−S_N|≤|S_{N+1}−S_N|=b_{n+1}. \nonumber \]
Fikiria mfululizo mbadala wa fomu
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]au\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
kwamba satisfies hypotheses ya mtihani alternating mfululizo. Hebu\( S\) kuashiria jumla ya mfululizo na\( S_N\) ueleze jumla ya\(N^{\text{th}}\) sehemu. Kwa integer yoyote\( N≥1\), salio\( R_N=S−S_N\) satisfies
\[|R_N|≤b_{N+1}. \nonumber \]
Kwa maneno mengine, ikiwa hali ya mtihani wa mfululizo unaotumika, basi hitilafu katika kukadiria mfululizo usio na kipimo kwa jumla ya\(N^{\text{th}}\) sehemu\( S_N\) ni ukubwa wa ukubwa wa muda ujao\( b_{N+1}\).
Fikiria mfululizo wa kubadilisha
\[ \sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n^2}. \nonumber \]
Matumizi makadirio salio kuamua amefungwa juu ya makosa\( R_{10}\) kama sisi takriban jumla ya mfululizo na jumla ya sehemu\( S_{10}\).
Suluhisho
Kutoka kwa theorem iliyoelezwa hapo juu,\[ |R_{10}|≤b_{11}=\dfrac{1}{11^2}≈0.008265. \nonumber \]
Kupata amefungwa kwa\( R_{20}\) wakati makadirio\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n}\) na\( S_{20}\).
- Kidokezo
-
\( |R_{20}|≤b_{21}\)
- Jibu
-
\( 0.04762\)
Muunganiko kamili na Masharti
Fikiria mfululizo\(\displaystyle \sum_{n=1}^∞a_n\) na mfululizo unaohusiana\(\displaystyle \sum_{n=1}^∞|a_n|\). Hapa tunazungumzia uwezekano wa uhusiano kati ya muunganiko wa mfululizo huu wawili. Kwa mfano, fikiria mfululizo wa harmonic mbadala\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n}\). Mfululizo ambao maneno yake ni thamani kamili ya maneno haya ni mfululizo wa harmonic,\(\displaystyle \sum_{n=1}^∞\left|\frac{(−1)^{n+1}}{n}\right|=\sum_{n=1}^∞\frac{1}{n}.\) tangu Tangu mfululizo wa harmonic unabadilika, lakini mfululizo wa harmonic hupungua, tunasema mfululizo wa harmonic unaonyesha muunganiko wa masharti.
Kwa kulinganisha, fikiria mfululizo\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}.\) Mfululizo ambao maneno yake ni maadili kamili ya maneno ya mfululizo huu ni mfululizo\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}.\) Tangu mfululizo huu wote hujiunga, tunasema mfululizo\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}\) unaonyesha muunganiko kamili.
Mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) unaonyesha muunganiko kabisa ikiwa\(\displaystyle \sum^∞_{n=1}|a_n|\) hujiunga. Mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) unaonyesha muunganiko wa masharti ikiwa\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga lakini\(\displaystyle \sum^∞_{n=1}|a_n|\) hutofautiana.
Kama inavyoonekana kwa mfululizo alternating harmonic, mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) inaweza kubadilika, lakini\(\displaystyle \sum^∞_{n=1}|a_n|\) inaweza kutofautiana. Katika theorem ifuatayo, hata hivyo, tunaonyesha kwamba ikiwa\(\displaystyle \sum^∞_{n=1}|a_n|\) hujiunga, kisha\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga.
Ikiwa\(\displaystyle \sum^∞_{n=1}|a_n|\) hujiunga, kisha\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga.
Tuseme kwamba\(\displaystyle \sum_{n=1}^∞|a_n|\) hujiunga. Tunaonyesha hili kwa kutumia ukweli kwamba\( a_n=|a_n\) au\( a_n=−|a_n|\) kwa hiyo\( |a_n|+a_n=2|a_n|\) au\( |a_n|+a_n=0\). Kwa hiyo,\( 0≤|a_n|+a_n≤2|a_n|\). Kwa hiyo, kwa mtihani wa kulinganisha, tangu\( 2\sum^∞_{n=1}|a_n|\) hujiunga, mfululizo
\[\sum_{n=1}^∞(|a_n|+a_n) \nonumber \]
hukutana. Kwa kutumia mali algebraic kwa mfululizo convergent, sisi kuhitimisha kwamba
\[\sum_{n=1}^∞a_n=\sum_{n=1}^∞(|a_n|+a_n)−\sum_{n=1}^∞|a_n| \nonumber \]
hukutana.
□
Kwa kila mfululizo wafuatayo, onyesha kama mfululizo unajiunga kabisa, hujiunga na hali ya kimwili, au hutofautiana.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\)
- \(\displaystyle \sum^∞_{n=1}\frac{\cos(n)}{n^2}\)
Suluhisho
tunaweza kuona kwamba
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{(−1)^{n+1}}{3n+1}\right|=\sum_{n=1}^∞\dfrac{1}{3n+1}\)
diverges kwa kutumia kikomo kulinganisha mtihani na mfululizo harmonic. Kwa kweli,
\(\displaystyle \lim_{n→∞}\dfrac{1/(3n+1)}{1/n}=\dfrac{1}{3}\).
Kwa hiyo, mfululizo hauunganishi kabisa. Hata hivyo, tangu
\( \dfrac{1}{3(n+1)+1}<\dfrac{1}{3n+1}\)na\( \dfrac{1}{3n+1}→0\),
mfululizo hujiunga. Tunaweza kuhitimisha kwamba\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\) hujiunga na hali ya kimwili.
b\( |\cos n|≤1,\) Kubainisha kuwa kuamua kama mfululizo converges kabisa, kulinganisha
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{\cos n}{n^2}\right|\)
na mfululizo\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\). Kwa kuwa\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\) hujiunga, kwa mtihani wa kulinganisha,\(\displaystyle \sum^∞_{n=1}\left|\frac{\cos n}{n^2}\right|\) hujiunga, na hivyo\(\displaystyle \sum^∞_{n=1}\frac{\cos n}{n^2}\) hujiunga kabisa.
Kuamua kama mfululizo\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2n^3+1}\) unajiunga kabisa, hujiunga na hali ya kimwili, au hutofautiana.
- Kidokezo
-
Angalia kwa muunganiko kabisa kwanza.
- Jibu
-
Mfululizo hujiunga kabisa.
Kuona tofauti kati ya muunganiko kamili na masharti, angalia kile kinachotokea wakati tunapanga upya masharti ya mfululizo wa harmonic mbadala\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n}\). Tunaonyesha kwamba tunaweza kupanga upya masharti ili mfululizo mpya ugeuke. Hakika ikiwa tunapanga upya masharti ya jumla ya mwisho, jumla haibadilika. Tunapofanya kazi kwa jumla isiyo na kipimo, hata hivyo, mambo ya kuvutia yanaweza kutokea.
Kuanza kwa kuongeza kutosha ya suala chanya kuzalisha kiasi kwamba ni kubwa kuliko baadhi\( M=10\) ya idadi halisi Kwa mfano, basi\( M=10,\) na kupata integer\( k\) vile
\[1+\dfrac{1}{3}+\dfrac{1}{5}+⋯+\dfrac{1}{2k−1}>10 \nonumber \]
(Tunaweza kufanya hivyo kwa sababu mfululizo\(\displaystyle \sum^∞_{n=1}\frac{1}{2n−1}\) diverges kwa infinity.) Kisha uondoe\( 1/2\). Kisha kuongeza maneno mazuri zaidi mpaka jumla itakapofikia 100. Hiyo ni, kupata mwingine integer\( j>k\) vile kwamba
\[(1+\dfrac{1}{3}+⋯+\dfrac{1}{2k−1}−\dfrac{1}{2}+\dfrac{1}{2k+1}+ \ldots +\dfrac{1}{2j+1}>100. \nonumber \]
Kisha Ondoa\( 1/4.\) Kuendelea kwa njia hii, tumegundua njia ya upya masharti katika mfululizo wa harmonic mbadala ili mlolongo wa kiasi cha sehemu ya mfululizo uliowekwa upya haupatikani na kwa hiyo hupungua.
Masharti katika mfululizo wa harmonic mbadala yanaweza pia kupangwa upya ili mfululizo mpya uunganishe kwa thamani tofauti. Katika Mfano, tunaonyesha jinsi ya kupanga upya masharti ili kuunda mfululizo mpya unaogeuka\( 3\ln(2)/2\). Tunasema kuwa mfululizo wa harmonic unaobadilisha unaweza kupangwa upya ili kuunda mfululizo unaojiunga na idadi yoyote halisi\( r\); hata hivyo, ushahidi wa ukweli huo ni zaidi ya upeo wa maandishi haya.
Kwa ujumla, mfululizo wowote\(\displaystyle \sum^∞_{n=1}a_n\) unaojiunga na hali unaweza kupangwa upya ili mfululizo mpya ugeuke au ugeuke kwa nambari tofauti halisi. Mfululizo unaojiunga kabisa hauna mali hii. Kwa mfululizo wowote\(\displaystyle \sum^∞_{n=1}a_n\) unaojiunga kabisa, thamani ya\(\displaystyle \sum^∞_{n=1}a_n\) ni sawa kwa upyaji wowote wa masharti. Matokeo haya inajulikana kama Theorem Riemann Rearrangement, ambayo ni zaidi ya wigo wa kitabu hiki.
Tumia ukweli kwamba
\[ 1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−⋯=\ln 2 \nonumber \]
kupanga upya masharti katika mfululizo wa harmonic mbadala hivyo jumla ya mfululizo upya ni\( 3\ln (2)/2.\)
Suluhisho
Hebu
\[ \sum_{n=1}^∞a_n=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−\dfrac{1}{6}+\dfrac{1}{7}−\dfrac{1}{8}+⋯. \nonumber \]
Tangu\(\displaystyle \sum_{n=1}^∞a_n=\ln (2)\), na mali algebraic ya mfululizo convergent,
\[ \sum_{n=1}^∞\dfrac{1}{2}a_n=\dfrac{1}{2}−\dfrac{1}{4}+\dfrac{1}{6}−\dfrac{1}{8}+⋯=\dfrac{1}{2}\sum_{n=1}^∞a_n=\dfrac{\ln 2}{2}. \nonumber \]
Sasa kuanzisha mfululizo\(\displaystyle \sum_{n=1}^∞b_n\) kama kwamba kwa wote\( n≥1, b_{2n−1}=0\) na\( b_{2n}=a_n/2.\) kisha
\[ \sum_{n=1}^∞b_n=0+\dfrac{1}{2}+0−\dfrac{1}{4}+0+\dfrac{1}{6}+0−\dfrac{1}{8}+⋯=\dfrac{\ln 2}{2}. \nonumber \]
Kisha kutumia mali ya kikomo cha algebraic ya mfululizo wa kubadilisha, tangu\(\displaystyle \sum_{n=1}^∞a_n\) na\(\displaystyle \sum_{n=1}^∞b_n\) kugeuka, mfululizo\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) hujiunga na
\[ \sum_{n=1}^∞(a_n+b_n)=\sum_{n=1}^∞a_n+\sum_{n=1}^∞b_n=\ln 2+\dfrac{\ln 2}{2}=\dfrac{3\ln 2}{2}. \nonumber \]
Sasa kuongeza masharti sambamba,\( a_n\) na\( b_n\), tunaona kwamba
\[ \sum_{n=1}^∞(a_n+b_n)=(1+0)+\left(−\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+0\right)+\left(−\dfrac{1}{4}−14\right)+\left(\dfrac{1}{5}+0\right)+\left(−\dfrac{1}{6}+\dfrac{1}{6}\right)+\left(\dfrac{1}{7}+0\right)+\left(\dfrac{1}{8}−\dfrac{1}{8}\right)+⋯=1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯. \nonumber \]
Tunaona kwamba mfululizo upande wa kulia wa ishara sawa ni rearrangement ya mfululizo alternating harmonic. Tangu\(\displaystyle \sum_{n=1}^∞(a_n+b_n)=3\ln (2)/2,\) sisi kuhitimisha kwamba
\[ 1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯=\dfrac{3\ln (2)}{2}. \nonumber \]
Kwa hiyo, tumegundua rearrangement ya mfululizo alternating harmonic kuwa mali taka.
Dhana muhimu
- Kwa mfululizo alternating\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n,\) kama\( b_{k+1}≤b_k\) kwa wote\( k\) na\( b_k→0\) kama\( k→∞,\) mfululizo alternating hujiunga.
- Ikiwa\(\displaystyle \sum^∞_{n=1}|a_n|\) hujiunga, kisha\(\displaystyle \sum^∞_{n=1}a_n\) hujiunga.
Mlinganyo muhimu
- Mfululizo mbadala
\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+⋯\)au
\(\displaystyle \sum_{n=1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−⋯\)
faharasa
- muunganiko kabisa
- ikiwa mfululizo\(\displaystyle \sum^∞_{n=1}|a_n|\) unajiunga, mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) unasemekana kugeuka kabisa
- mfululizo mbadala
- mfululizo wa fomu\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) au\(\displaystyle \sum^∞_{n=1}(−1)^nb_n\), wapi\( b_n≥0\), inaitwa mfululizo wa kubadilisha
- kubadilisha mfululizo mtihani
- kwa mfululizo mbadala wa fomu yoyote, ikiwa\( b_{n+1}≤b_n\) kwa integers zote\( n≥1\) na\( b_n→0\), basi mfululizo wa kubadilisha hujiunga
- muunganiko wa masharti
- ikiwa mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) unajiunga, lakini mfululizo\(\displaystyle \sum^∞_{n=1}|a_n|\) unajitokeza, mfululizo\(\displaystyle \sum^∞_{n=1}a_n\) unasemekana kugeuka kwa hali ya kimwili


