8.5: Ulinganisho wa mstari wa kwanza

Malengo ya kujifunza

• Andika equation ya kwanza ya mstari tofauti katika fomu ya kawaida.
• Pata kipengele cha kuunganisha na uitumie kutatua usawa wa kutofautiana wa mstari wa kwanza.
• Tatua matatizo yaliyotumika yanayohusisha equations ya kwanza ya mstari tofauti.

Mapema, tulijifunza matumizi ya equation ya kwanza ya tofauti ambayo ilihusisha kutatua kwa kasi ya kitu. Hasa, ikiwa mpira unatupwa juu na kasi ya awali ya\( v_0\) ft/s, basi tatizo la thamani ya awali linaloelezea kasi ya mpira baada ya\( t\) sekunde hutolewa na

\[ \dfrac{dv}{dt}=−32 \nonumber \]

na\(v(0)=v_0.\)

Mfano huu unafikiri kwamba nguvu pekee inayofanya mpira ni mvuto. Sasa tunaongeza tatizo kwa kuruhusu uwezekano wa upinzani wa hewa unaofanya mpira.

Upinzani wa hewa daima hufanya katika mwelekeo kinyume na mwendo. Kwa hiyo, ikiwa kitu kinaongezeka, upinzani wa hewa hufanya mwelekeo wa chini. Ikiwa kitu kinaanguka, upinzani wa hewa hufanya mwelekeo wa juu (Kielelezo\( \PageIndex{1}\)). Hakuna uhusiano halisi kati ya kasi ya kitu na upinzani wa hewa unaofanya juu yake. Kwa vitu vidogo sana, upinzani wa hewa ni sawia na kasi; yaani, nguvu kutokana na upinzani wa hewa ni nambari sawa na nyakati za mara kwa\( k\) mara\( v\). Kwa vitu vikubwa (kwa mfano, ukubwa wa baseball), kulingana na sura, upinzani wa hewa unaweza kuwa takriban sawia na mraba wa kasi. Kwa kweli, upinzani hewa inaweza kuwa sawia na\( v^{1.5}\), au\( v^{0.9}\), au baadhi ya nguvu nyingine ya\( v\).

Kielelezo\( \PageIndex{1}\): Vikosi vinavyofanya baseball inayohamia: mvuto hufanya katika mwelekeo wa chini na upinzani wa hewa hufanya mwelekeo kinyume na mwelekeo wa mwendo.

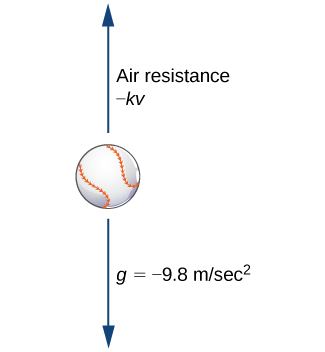
Tutafanya kazi na makadirio ya mstari wa upinzani wa hewa. Ikiwa tunadhani\( k>0\), basi maneno ya nguvu\( F_A\) kutokana na upinzani wa hewa hutolewa na\( FA_=−kv\). Kwa hiyo jumla ya nguvu zinazofanya kitu ni sawa na jumla ya nguvu ya mvuto na nguvu kutokana na upinzani wa hewa. Hii, kwa upande wake, ni sawa na wingi wa kitu kilichoongezeka kwa kasi yake kwa wakati\( t\) (sheria ya pili ya Newton). Hii inatupa equation tofauti

\[ m\dfrac{dv}{dt}=−kv−mg. \nonumber \]

Hatimaye, sisi kulazimisha hali ya awali\( v(0)=v_0,\) ambapo\( v_0\) ni kasi ya awali kipimo katika mita kwa pili. Hii inafanya\( g=9.8m/s^2.\) Tatizo la thamani ya awali inakuwa

\[ m\dfrac{dv}{dt}=−kv−mg \nonumber \]

na\(v(0)=v_0.\)

Equation tofauti katika tatizo hili la thamani ya awali ni mfano wa equation ya kwanza ya mstari tofauti. (Kumbuka kwamba tofauti equation ni ya kwanza ili kama juu ili derivative kwamba inaonekana katika equation ni\( 1\).) Katika sehemu hii, tunasoma equations ya kwanza ya mstari na kuchunguza njia ya kutafuta suluhisho la jumla kwa aina hizi za equations, pamoja na kutatua matatizo ya thamani ya awali inayowashirikisha.

Ufafanuzi: Linear kwanza ili tofauti equation

Equation tofauti ya utaratibu wa kwanza ni mstari ikiwa inaweza kuandikwa kwa fomu

\[a(x)y′+b(x)y=c(x), \nonumber \]

ambapo\( a(x),b(x),\) na\( c(x)\) ni holela kazi ya\( x\).

Kumbuka kwamba kazi haijulikani\( y\) inategemea variable\( x\); yaani,\( x\) ni variable huru na\( y\) ni variable tegemezi. Baadhi ya mifano ya equations ya kwanza ya mstari tofauti ni

\[ (3x^2−4)y'+(x−3)y=\sin x \nonumber \]

\[ (\sin x)y'−(\cos x)y=\cot x \nonumber \]

\[ 4xy'+(3\ln x)y=x^3−4x. \nonumber \]

Mifano ya equations ya kwanza isiyo ya kawaida ya kutofautiana ni pamoja na

\[ (y')^4−(y')^3=(3x−2)(y+4) \nonumber \]

\[ 4y'+3y^3=4x−5 \nonumber \]

\[(y')^2=\sin y+\cos x. \nonumber \]

Hizi milinganyo ni nonlinear kwa sababu ya maneno kama\( (y′)^4,y^3,\) n.k Kutokana na masharti haya, haiwezekani kuweka equations hizi katika fomu sawa na Equation.

Fomu ya kawaida

Fikiria equation tofauti

\[ (3x^2−4)y′+(x−3)y=\sin x. \nonumber \]

Lengo letu kuu katika sehemu hii ni kupata njia ya suluhisho kwa usawa wa fomu hii. Ni muhimu kuwa na mgawo wa\( y′\) kuwa sawa na\( 1\). Ili kufanya hivyo kutokea, tunagawanya pande zote mbili\( 3x^2−4.\)

\[ y′+ \left(\dfrac{x−3}{3x^2−4} \right)y=\dfrac{\sin x}{3x^2−4} \nonumber \]

Hii inaitwa fomu ya kawaida ya equation tofauti. Tutatumia baadaye wakati wa kutafuta suluhisho la equation ya kawaida ya kwanza ya mstari tofauti. Kurudi Equation, tunaweza kugawanya pande zote mbili za equation na\( a(x)\). Hii inasababisha equation

\[ y′+\dfrac{b(x)}{a(x)}y=\dfrac{c(x)}{a(x)}. \label{eq5} \]

Sasa kufafanua

\[ p(x)=\dfrac{b(x)}{a(x)} \nonumber \]

na

\[ q(x)=\dfrac{c(x)}{a(x)} \nonumber \]

Kisha Equation\ ref {eq5} inakuwa

\[ y′+p(x)y=q(x). \nonumber \]

Tunaweza kuandika yoyote ya kwanza ili linear tofauti equation katika fomu hii, na hii inajulikana kama fomu ya kiwango kwa ajili ya kwanza ili linear tofauti equation.

Mfano\( \PageIndex{1}\): Writing First-Order Linear Equations in Standard Form

Weka kila moja ya usawa wa kwanza wa mstari wa mstari wa kwanza katika fomu ya kawaida. Kutambua\( p(x)\) na\( q(x)\) kwa kila equation.

1. \( y'=3x−4y\)
2. \( \dfrac{3xy'}{4y−3}=2\)(hapa\( x>0\))
3. \( y=3y'−4x^2+5\)

Suluhisho

a\( 4y\) Ongeza pande zote mbili:

\( y'+4y=3x.\)

Katika equation hii,\( p(x)=4\) na\ | (q (x) =3x.\)

b Kuzidisha pande zote mbili na\( 4y−3\), kisha uondoe\( 8y\) kutoka kila upande:

\( \dfrac{3xy'}{4y−3}=2\)

\( 3xy'=2(4y−3)\)

\( 3xy'=8y−6\)

\( 3xy'−8y=−6.\)

Hatimaye, kugawanya pande zote mbili kwa\( 3x\) kufanya mgawo wa\( y'\) sawa na\( 1\):

\( y'−\dfrac{8}{3x}y=−\dfrac{2}{3x}.\)

Hii ni halali kwa sababu katika taarifa ya awali ya tatizo hili sisi kudhani kuwa\( x>0\). (Kama\( x=0\) basi equation ya awali inakuwa\( 0=2\), ambayo ni wazi taarifa ya uongo.)

Katika equation hii,\( p(x)=−\dfrac{8}{3x}\) na\( q(x)=−\dfrac{2}{3x}\).

c Ondoa\( y\) kutoka kila upande na kuongeza\( 4x^2−5\):

\( 3y'−y=4x^2−5.\)

Kisha ugawanye pande zote mbili na\( 3\):

\( y'−\dfrac{1}{3}y=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

Katika equation hii,\( p(x)=−\dfrac{1}{3}\) na\( q(x)=\dfrac{4}{3}x^2−\dfrac{5}{3}\).

Zoezi\(\PageIndex{1}\)

Weka equation\( \dfrac{(x+3)y'}{2x−3y−4}=5\) katika fomu ya kawaida na kutambua\( p(x)\) na\( q(x)\).

Kidokezo

Kuzidisha pande zote mbili kwa denominator ya kawaida, kisha kukusanya maneno yote\( y\) yanayohusisha upande mmoja.

Jibu

\[ y'+\dfrac{15}{x+3}y=\dfrac{10x−20}{x+3} \nonumber \]

\[p(x)=\dfrac{15}{x+3} \nonumber \]

na

\[ q(x)=\dfrac{10x−20}{x+3} \nonumber \]

Kuunganisha Mambo

Sasa tunaendeleza mbinu ya suluhisho kwa equation yoyote ya kwanza ya mstari tofauti. Tunaanza na fomu ya kawaida ya usawa wa mstari wa kwanza wa mstari:

\[ y'+p(x)y=q(x). \label{Deq1} \]

Muda wa kwanza upande wa kushoto wa Equation ni derivative ya kazi haijulikani, na muda wa pili ni bidhaa ya kazi inayojulikana na kazi haijulikani. Hii ni sawa na utawala wa nguvu. Ikiwa tunazidisha Equation\ ref {Deq1} na kazi iliyowekwa bado\( μ(x)\), basi equation inakuwa

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq2} \]

Upeo wa upande wa kushoto\ ref {Deq2} unaweza kuendana kikamilifu na utawala wa bidhaa:

\[ \dfrac{d}{dx}[f(x)g(x)]=f′(x)g(x)+f(x)g′(x). \nonumber \]

Vinavyolingana mrefu kwa muda anatoa\( y=f(x),g(x)=μ(x)\), na\( g′(x)=μ(x)p(x)\). Kuchukua derivative ya\( g(x)=μ(x)\) na kuweka sawa na upande wa kulia wa\( g′(x)=μ(x)p(x)\) inaongoza kwa

\[ μ′(x)=μ(x)p(x). \nonumber \]

Hii ni ya kwanza ili, kutenganishwa tofauti equation kwa\(μ(x).\) Tunajua\( p(x)\) kwa sababu inaonekana katika equation tofauti sisi ni kutatua. Kutenganisha vigezo na kuunganisha mavuno

\[ \begin{align} \dfrac{μ′(x)}{μ(x)} =p(x) \\[4pt] ∫\dfrac{μ′(x)}{μ(x)}dx =∫p(x)dx \\[4pt] \ln|μ(x)| =∫p(x)dx+C \\[4pt] e^{\ln|μ(x)|} =e^{∫p(x)dx+C} \\[4pt] |μ(x)| =C_1e^{∫p(x)dx} \\[4pt] μ(x) =C_2e^{∫p(x)dx}. \end{align} \nonumber \]

Hapa\( C_2\) inaweza kuwa kiholela (chanya au hasi) mara kwa mara. Hii inasababisha njia ya jumla ya kutatua usawa wa mstari wa kwanza wa mstari. Sisi kwanza kuzidisha pande zote mbili za Equation kwa sababu kuunganisha\( μ(x).\) Hii inatoa

\[ μ(x)y′+μ(x)p(x)y=μ(x)q(x). \label{Deq5} \]

Upande wa kushoto wa Equation\ ref {Deq5} inaweza kuandikwa upya kama\( \dfrac{d}{dx}(μ(x)y)\).

\[ \dfrac{d}{dx}(μ(x)y)=μ(x)q(x). \label{Deq6} \]

Next kuunganisha pande zote mbili za Equation\ ref {Deq6} kwa heshima na\(x\).

\[ \begin{align} ∫\dfrac{d}{dx}(μ(x)y)dx =∫μ(x)q(x)dx \\[4pt] μ(x)y =∫μ(x)q(x)dx \label{Deq7} \end{align} \]

Gawanya pande zote mbili za Equation\ ref {Deq6} na\( μ(x)\):

\[ y=\dfrac{1}{μ(x)}\left[∫μ(x)q(x)dx+C\right]. \nonumber \]

Tangu\( μ(x)\) hapo awali mahesabu, sisi ni sasa kumaliza. Kumbuka muhimu kuhusu mara kwa mara kuunganisha\( C\): Inaweza kuonekana kwamba sisi ni haiendani katika matumizi ya mara kwa mara kuunganisha. Hata hivyo,\( p(x)\) ushirikishwaji muhimu ni muhimu ili kupata kipengele cha kuunganisha kwa Equation. Sababu moja tu ya kuunganisha inahitajika ili kutatua equation; kwa hiyo, ni salama kugawa thamani\(C\) kwa hili muhimu. Tulichagua\(C=0\). Wakati wa kuhesabu muhimu ndani ya mabano katika Equation, ni muhimu kuweka chaguzi zetu wazi kwa thamani ya mara kwa mara kuunganisha, kwa sababu lengo letu ni kupata familia ya jumla ya ufumbuzi wa Equation. Sababu hii ya kuunganisha inathibitisha tu.

Mkakati wa Kutatua Matatizo: Kutatua Ulinganisho wa Tofauti ya Linear ya Kwanza

1. Weka equation katika fomu ya kawaida na kutambua\( p(x)\) na\( q(x)\).
2. Tumia sababu ya kuunganisha\[ μ(x)=e^{∫p(x)dx}. \nonumber \]
3. Kuzidisha pande zote mbili za equation tofauti na\( μ(x)\).
4. Unganisha pande zote mbili za equation kupatikana katika hatua\( 3\), na kugawanya pande zote mbili kwa\( μ(x)\).
5. Ikiwa kuna hali ya awali, tambua thamani ya\( C\).

Mfano\( \PageIndex{2}\): Solving a First-order Linear Equation

Kupata ufumbuzi wa jumla kwa equation tofauti\( xy'+3y=4x^2−3x.\) Kudhani\( x>0.\)

Suluhisho

1. Ili kuweka equation hii tofauti katika fomu ya kawaida, kugawanya pande zote mbili na\( x\):

\[ y'+\dfrac{3}{x}y=4x−3. \nonumber \]

Kwa hiyo\( p(x)=\dfrac{3}{x}\) na\( q(x)=4x−3.\)

2. Sababu ya kuunganisha ni\( μ(x)=e^{∫(3/x)}dx=e^{3 \ln x}=x^3\).

3. Kuzidisha pande zote mbili za equation tofauti na\( μ(x)\) inatupa

\[ \begin{align*} x^3y′+x^3(\dfrac{3}{x}) =x^3(4x−3) \\[4pt] x^3y′+3x^2y =4x^4−3x^3 \\[4pt] \dfrac{d}{dx}(x^3y) = 4x^4−3x^3. \end{align*}\]

4. Unganisha pande zote mbili za equation.

\[ \begin{align*} ∫\dfrac{d}{dx}(x^3y)dx = ∫4x^4−3x^3dx \\[4pt] x^3y =\dfrac{4x^5}{5}−\dfrac{3x^4}{4}+C \\[4pt] y =\dfrac{4x^2}{5}−\dfrac{3x}{4}+Cx^{−3}. \end{align*}\]

5. Hakuna thamani ya awali, hivyo tatizo limekamilika.

Uchambuzi

Huenda umeona hali iliyowekwa kwenye equation tofauti; yaani,\( x>0\). Kwa thamani yoyote nonzero ya\( C\), ufumbuzi wa jumla si defined katika\( x=0\). Zaidi ya hayo\( x<0\), wakati, kuunganisha sababu mabadiliko. sababu kuunganisha ni iliyotolewa na Equation kama\( f(x)=e^{∫p(x)dx}\). Kwa hili\( p(x)\) tunapata

\[ \begin{align*} e^{∫p(x)dx} =e^{∫(3/x)dx} \\[4pt] =e^{3\ln|x|} \\[4pt] =|x|^3 \end{align*}\]

tangu\(x<0\). Tabia ya suluhisho la jumla hubadilika kwa\( x=0\) kiasi kikubwa kutokana na ukweli ambao\( p(x)\) haujafafanuliwa hapo.

Zoezi\(\PageIndex{2}\)

Kupata ufumbuzi wa jumla wa tofauti equation\( (x−2)y'+y=3x^2+2x.\) kudhani\( x>2\).

Kidokezo

Tumia njia iliyoainishwa katika mkakati wa kutatua matatizo kwa equations ya kwanza ya mstari tofauti.

Jibu

\( y=\dfrac{x^3+x^2+C}{x−2}\)

Sasa tunatumia mkakati huo ili kupata suluhisho la tatizo la thamani ya awali.

Mfano\( \PageIndex{3}\): A First-order Linear Initial-Value Problem

Tatua tatizo la thamani ya awali

\[ y′+3y=2x−1,y(0)=3. \nonumber \]

Suluhisho

1. Equation hii tofauti tayari iko katika fomu ya kawaida na\( p(x)=3\) na\( q(x)=2x−1\).

2. Sababu ya kuunganisha ni\( μ(x)=e^{∫3dx}=e^{3x}\).

3. Kuzidisha pande zote mbili za equation tofauti na\( μ(x)\) anatoa

\[ \begin{align*} e^{3x}y′+3e^{3x}y =(2x−1)e^{3x} \\[4pt] \dfrac{d}{dx}[ye^{3x}] =(2x−1)e^{3x}. \end{align*}\]

Unganisha pande zote mbili za equation:

\( ∫\dfrac{d}{dx}[ye^{3x}]dx=∫(2x−1)e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}}{3}(2x−1)−∫\dfrac{2}{3}e^{3x}dx\)

\( ye^{3x}=\dfrac{e^{3x}(2x−1)}{3}−\dfrac{2e^{3x}}{9}+C\)

\( y=\dfrac{2x−1}{3}−\dfrac{2}{9}+Ce^{−3x}\)

\( y=\dfrac{2x}{3}−\dfrac{5}{9}+Ce^{−3x}\).

4. Sasa mbadala\( x=0\) na\( y=3\) katika suluhisho la jumla na kutatua kwa\( C\):

\[ \begin{align*} y =\dfrac{2}{3}x−\dfrac{5}{9}+Ce^{−3x} \\[4pt] 3 =\dfrac{2}{3}(0)−\dfrac{5}{9}+Ce^{−3(0)} \\[4pt] 3 =−\dfrac{5}{9}+C \\[4pt] C=\dfrac{32}{9}. \end{align*}\]

Kwa hiyo, suluhisho la tatizo la thamani ya awali ni

\[ y=\dfrac{2}{3}x−\dfrac{5}{9}+\dfrac{32}{9}e^{−3x}. \nonumber \]

Mfano\(\PageIndex{4}\):

Tatua tatizo la thamani ya awali\[ y'−2y=4x+3y(0)=−2. \nonumber \]

Suluhisho

\[ y=−2x−4+2e^{2x} \nonumber \]

Matumizi ya Ulinganisho wa Tofauti ya Linear ya Kwanza

Tunaangalia maombi mawili tofauti ya usawa wa mstari wa kwanza wa mstari. Ya kwanza inahusisha upinzani wa hewa kama inahusiana na vitu vinavyoongezeka au kuanguka; pili inahusisha mzunguko wa umeme. Maombi mengine ni mengi, lakini wengi hutatuliwa kwa mtindo sawa.

Kuanguka kwa bure na upinzani wa hewa

Tulijadili upinzani wa hewa mwanzoni mwa sehemu hii. Mfano unaofuata unaonyesha jinsi ya kutumia dhana hii kwa mpira katika mwendo wa wima. Sababu nyingine zinaweza kuathiri nguvu ya upinzani wa hewa, kama ukubwa na sura ya kitu, lakini tunawapuuza hapa.

Mfano\( \PageIndex{5}\): A Ball with Air Resistance

Racquetball ni hit moja kwa moja juu na kasi ya awali ya\( 2\) m/s. wingi wa racquetball ni takriban\( 0.0427\) kilo. Upinzani wa hewa hufanya mpira kwa nguvu numerically sawa na\( 0.5v\), ambapo\( v\) inawakilisha kasi ya mpira kwa wakati\( t\).

1. Find kasi ya mpira kama kazi ya muda.
2. Inachukua muda gani kwa mpira kufikia urefu wake wa juu?
3. Ikiwa mpira unapigwa kutoka urefu wa awali wa\( 1\) mita, ni juu gani utafikia?

Suluhisho

a. wingi\( m=0.0427kg,k=0.5,\) na\( g=9.8m/s^2\). Kasi ya awali ni\( v_0=2 m/s\). Kwa hiyo, tatizo la thamani ya awali ni

\( 0.0427\dfrac{dv}{dt}=−0.5v−0.0427(9.8),v_0=2.\)

Kugawanya equation tofauti na\( 0.0427\) anatoa

\( \dfrac{dv}{dt}=−11.7096v−9.8,v_0=2.\)

Equation tofauti ni linear. Kutumia mkakati wa kutatua matatizo kwa equations tofauti ya mstari:

Hatua ya 1. Andika upya equation tofauti kama\( \dfrac{dv}{dt}+11.7096v=−9.8\). Hii inatoa\( p(t)=11.7096\) na\( q(t)=−9.8\)

Hatua ya 2. Sababu ya kuunganisha ni\( μ(t)=e^{∫11.7096dt}=e^{11.7096t}.\)

Hatua ya 3. Panua equation tofauti na\( μ(t)\):

\( e^{11.7096t\dfrac{dv}{dt}}+11.7096ve^{11.7096t}=−9.8e^{11.7096t}\)

\( \dfrac{d}{dt}[ve^{11.7096t}]=−9.8e^{11.7096t}.\)

Hatua ya 4. Unganisha pande zote mbili:

\( ∫\dfrac{d}{dt}[ve^{11.7096t}]dt=∫−9.8e^{11.7096t}dt\)

\( ve^{11.7096t}=\dfrac{−9.8}{11.7096}e^{11.7096t}+C\)

\( v(t)=−0.8369+Ce^{−11.7096t}.\)

Hatua ya 5. Tatua kwa\( C\) kutumia hali ya awali\( v_0=v(0)=2\):

\( v(t)=−0.8369+Ce^{−11.7096t}\)

\( v(0)=−0.8369+Ce^{−11.7096(0)}\)

\( 2=−0.8369+C\)

\( C=2.8369.\)

Kwa hiyo, suluhisho la tatizo la thamani ya awali ni

\( v(t)=2.8369e^{−11.7096t}−0.8369.\)

b. mpira hufikia urefu wake wa juu wakati kasi ni sawa na sifuri. Sababu ni kwamba wakati kasi ni chanya, inaongezeka, na wakati ni hasi, inaanguka. Kwa hiyo, ikiwa ni sifuri, haitoi wala kuanguka, na iko katika urefu wake wa juu.

\( 2.8369e^{−11.7096t}−0.8369=0\)

\( 2.8369e^{−11.7096t}=0.8369\)

\( e^{−11.7096t}=\dfrac{0.8369}{2.8369}≈0.295\)

\( lne^{−11.7096t}=ln0.295≈−1.221\)

\( −11.7096t=−1.221\)

\( t≈0.104.\)

Kwa hiyo inachukua takriban\( 0.104\) pili kufikia urefu wa juu.

c Ili kupata urefu wa mpira kama kazi ya wakati, tumia ukweli kwamba derivative ya nafasi ni kasi, yaani, ikiwa\( h(t)\) inawakilisha urefu kwa wakati\( t\), basi\( h′(t)=v(t)\). Kwa sababu tunajua\( v(t)\) na urefu wa awali, tunaweza kuunda tatizo la thamani ya awali:

\( h′(t)=2.8369e^{−11.7096t}−0.8369,h(0)=1.\)

Kuunganisha pande zote mbili za equation tofauti kwa heshima na\( t\) inatoa

\( ∫h′(t)dt=∫2.8369e^{−11.7096t}−0.8369dt\)

\( h(t)=−\dfrac{2.8369}{11.7096}e^{−11.7096t}−0.8369t+C\)

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C.\)

Tatua\( C\) kwa kutumia hali ya awali:

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+C\)

\( h(0)=−0.2423e^{−11.7096(0)}−0.8369(0)+C\)

\( 1=−0.2423+C\)

\( C=1.2423.\)

Kwa hiyo

\( h(t)=−0.2423e^{−11.7096t}−0.8369t+1.2423.\)

Baada ya\( 0.104\) pili, urefu hutolewa na

\( h(0.2)=−0.2423e^{−11.7096t}−0.8369t+1.2423≈1.0836\)mita.

Zoezi\(\PageIndex{3}\)

Uzito wa senti ni\(2.5\) gramu (United States Mint, “Coin Specifications,” iliyofikiwa Aprili 9, 2015, http://www.usmint.gov/about_the_mint...specifications), na staha ya juu ya uchunguzi wa Empire State Building iko\( 369\) mita juu ya barabara. Kwa kuwa senti ni kitu kidogo na laini, upinzani wa hewa unaofanya senti ni kweli ndogo sana. Tunadhani upinzani wa hewa ni sawa sawa na\( 0.0025v\). Zaidi ya hayo, senti imeshuka bila kasi ya awali iliyotolewa nayo.

1. Weka tatizo la awali la thamani ambalo linawakilisha senti ya kuanguka.
2. Tatua tatizo kwa\( v(t)\).
3. Je, ni kasi ya mwisho ya senti (yaani, kuhesabu kikomo cha kasi kama\( t\) inakaribia infinity)?

Kidokezo

Weka equation tofauti kwa njia sawa na Mfano. Kumbuka kubadilisha kutoka gramu hadi kilo.

Jibu

a.\( \dfrac{dv}{dt}=−v−9.8\)\( v(0)=0\)

b.\( v(t)=9.8(e^{−t}−1)\)

c.\( \lim_{t→∞}v(t)=\lim_{t→∞}(9.8(e^{−t}−1))=−9.8m/s≈−21.922mph\)

Circuits umeme

Chanzo cha nguvu ya umeme (kwa mfano, betri au jenereta) hutoa mtiririko wa sasa katika mzunguko uliofungwa, na sasa hii inazalisha kushuka kwa voltage katika kila resistor, inductor, na capacitor katika mzunguko. Kanuni ya Loop ya Kirchhoff inasema kwamba jumla ya matone ya voltage katika resistors, inductors, na capacitors ni sawa na nguvu ya jumla ya umeme katika mzunguko uliofungwa. Tuna matokeo matatu yafuatayo:

1. Kushuka kwa voltage katika kupinga hutolewa na

\( E_R=Ri,\)

ambapo\( R\) ni mara kwa mara ya uwiano aitwaye upinzani, na\( i\) ni ya sasa.

2. Kushuka kwa voltage katika inductor hutolewa na

\( EL=Li′\),

ambapo\( L\) ni mara kwa mara ya uwiano inayoitwa inductance, na\( i\) tena inaashiria sasa.

3. Kushuka kwa voltage katika capacitor hutolewa na

\( E_C=\dfrac{1}{C}q\),

wapi\( C\) mara kwa mara ya uwiano unaoitwa capacitance, na\( q\) ni malipo ya papo hapo juu ya capacitor. Uhusiano kati\( i\) na\( q\) ni\( i=q′\).

Tunatumia vitengo vya volts\( (V)\) kupima voltage\( E\), amperes\( (A)\) kupima sasa\( i\), coulombs\( (C)\) kupima malipo\( q\), ohms\( (Ω)\) kupima upinzani\( R\), henry\( (H)\) kupima inductance\( L\), na farads\( (F)\) kupima uwezo\( C\). Fikiria mzunguko katika Kielelezo\( \PageIndex{2}\).

Kielelezo\( \PageIndex{2}\): Mzunguko wa umeme wa kawaida, una jenereta ya voltage\( (V_S)\)\( (C)\), capacitor\( (L)\), inductor, na kupinga\( (R)\).

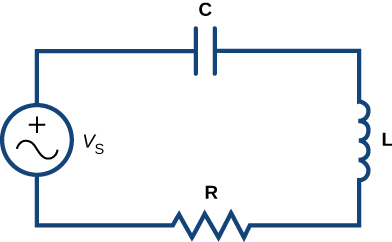
Kutumia Kanuni ya Loop ya Kirchhoff kwenye mzunguko huu, tunaruhusu\( E\) kuashiria nguvu ya umeme inayotolewa na jenereta ya voltage. Kisha

\( E_L+E_R+E_C=E\).

Kubadilisha maneno kwa\( E_L,E_R,\) na\( E_C\) katika equation hii, tunapata

\( Li′+Ri+\dfrac{1}{C}q=E.\)

Ikiwa hakuna capacitor katika mzunguko, basi equation inakuwa

\( Li′+R_i=E.\)

Hii ni ya kwanza ili tofauti equation katika\( i\). Mzunguko hujulikana kama\( LR\) mzunguko.

Kisha, tuseme hakuna inductor katika mzunguko, lakini kuna capacitor na kupinga, hivyo\( L=0,R≠0,\) na\( C≠0.\) Kisha Equation inaweza kuandikwa upya kama

\( Rq′+\dfrac{1}{C}q=E,\)

ambayo ni ya kwanza ili linear tofauti equation. Hii inajulikana kama mzunguko wa RC. Katika hali yoyote, tunaweza kuanzisha na kutatua tatizo la thamani ya awali.

Mzunguko wa umeme

mzunguko ina katika mfululizo nguvu electromotive\( E=50\sin 20tV,\) iliyotolewa na resistor ya\( 5Ω\), na inductor ya\( 0.4H\). Ikiwa sasa ya awali ni\( 0\), pata sasa kwa wakati\( t>0\).

Suluhisho

Tuna kupinga na inductor katika mzunguko, kwa hiyo tunatumia Equation. Kushuka kwa voltage katika kupinga hutolewa na\( E_R=R_i=5_i\). Kushuka kwa voltage katika inductor hutolewa na\( E_L=Li′=0.4i′\). Nguvu ya electromotive inakuwa upande wa kulia wa Equation. Kwa hiyo Equation inakuwa

\[ 0.4i′+5i=50\sin 20t. \nonumber \]

Kugawanya pande zote mbili kwa\( 0.4\) anatoa equation

\[ i′+12.5i=125\sin 20t. \nonumber \]

Kwa kuwa sasa ya awali ni 0, matokeo haya inatoa hali ya awali ya\( i(0)=0.\) Tunaweza kutatua tatizo hili la thamani ya awali kwa kutumia mkakati wa hatua tano kwa kutatua usawa wa kwanza wa tofauti.

Hatua ya 1. Andika upya equation tofauti kama\( i′+12.5i=125\sin 20t\). Hii inatoa\( p(t)=12.5\) na\( q(t)=125\sin 20t\).

Hatua ya 2. Sababu ya kuunganisha ni\( μ(t)=e^{∫12.5dt}=e^{12.5t}\).

Hatua ya 3. Panua equation tofauti na\( μ(t)\):

\( e^{12.5t}i′+12.5e^{12.5t}i=125e^{12.5t}\sin 20t\)

\( \dfrac{d}{dt}[ie^{12.5}t]=125e^{12.5t}\sin 20t\).

Hatua ya 4. Unganisha pande zote mbili:

\( ∫\dfrac{d}{dt}[ie^{12.5t}]dt=∫125e^{12.5t}\sin 20tdt\)

\( ie^{12.5t}=(\dfrac{250\sin 20t−400\cos 20t}{89})e^{12.5t}+C\)

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\).

Hatua ya 5. Tatua kwa\( C\) kutumia hali ya awali\( v(0)=2\):

\( i(t)=\dfrac{250\sin 20t−400\cos 20t}{89}+Ce^{−12.5t}\)

\( i(0)=\dfrac{250sin20(0)−400cos20(0)}{89}+Ce^{−12.5(0)}\)

\( 0=−\dfrac{400}{89}+C\)

\( C=\dfrac{400}{89}\).

Kwa hiyo, suluhisho la tatizo la thamani ya awali ni

\[ i(t)=\dfrac{250\sin 20t−400\cos 20t+400e^{−12.5t}}{89}=\dfrac{250\sin 20t−400\cos 20t}{89}+\dfrac{400e^{−12.5t}}{89}. \nonumber \]

Neno la kwanza linaweza kuandikwa upya kama kazi moja ya cosine. Kwanza, kuzidisha na ugawanye na\( \sqrt{250^2+400^2}=50\sqrt{89}\):

\( \dfrac{250\sin 20t−400\cos 20t}{89}=\dfrac{50\sqrt{89}}{89}(\dfrac{250\sin 20t−400\cos 20t}{50\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})\).

Next,\( φ\) kufafanua kuwa angle papo hapo kwamba\( \cos φ=\dfrac{8}{\sqrt{89}}\). Kisha\( \sin φ=\dfrac{5}{\sqrt{89}}\) na

\( −\dfrac{50\sqrt{89}}{89}(\dfrac{8\cos 20t}{\sqrt{89}}−\dfrac{5\sin 20t}{\sqrt{89}})=−\dfrac{50\sqrt{89}}{89}(\cos φ\cos 20t−\sin φ\sin 20t)=−\dfrac{50\sqrt{89}}{89}\cos(20t+φ).\)

Kwa hiyo, ufumbuzi unaweza kuandikwa kama

\( i(t)=−\dfrac{50\sqrt{89}}{89}cos(20t+φ)+\dfrac{400e^{−12.5t}}{89}\).

Neno la pili linaitwa muda wa kuzuia, kwa sababu hupotea haraka kama\( t\) inakua kubwa. Mabadiliko ya awamu hutolewa na\( φ\), na amplitude ya sasa ya hali ya kutosha hutolewa na\( \dfrac{50\sqrt{89}}{89}\). Grafu ya suluhisho hili inaonekana kwenye Kielelezo\( \PageIndex{3}\):

Kielelezo\( \PageIndex{3}\).

Zoezi\(\PageIndex{4}\)

Mzunguko una mfululizo wa nguvu ya umeme iliyotolewa na\( E=20sin5t\) V, capacitor yenye uwezo\( 0.02F\), na kupinga\( 8Ω\). Ikiwa malipo ya awali ni\( 4C\), pata malipo kwa wakati\( t>0\).

Kidokezo

Tumia Equation kwa\( RC\) mzunguko wa kuanzisha tatizo la thamani ya awali.

Jibu

Tatizo la thamani ya awali:

\( 8q′+\dfrac{1}{0.02}q=20sin5t,q(0)=4\)

\( q(t)=\dfrac{10sin5t−8cos5t+172e^{−6.25t}}{41}\)

Dhana muhimu

• Equation yoyote ya kwanza ya mstari wa mstari inaweza kuandikwa kwa fomu\( y'+p(x)y=q(x)\).
• Tunaweza kutumia mkakati wa kutatua matatizo ya hatua tano kwa kutatua usawa wa kutofautiana wa mstari wa kwanza ambao unaweza au usijumuishe thamani ya awali.
• Matumizi ya equations tofauti ya mstari wa kwanza ni pamoja na kuamua mwendo wa kitu cha kupanda au kuanguka na upinzani wa hewa na kutafuta sasa katika mzunguko wa umeme.

Mlinganyo muhimu

• fomu ya kawaida

\( y'+p(x)y=q(x)\)

• kuunganisha sababu

\( μ(x)=e^{∫p(x)dx}\)

faharasa

kuunganisha sababu

kazi yoyote\(f(x)\) ambayo ni kuongezeka kwa pande zote mbili za equation tofauti kufanya upande kuwashirikisha kazi haijulikani sawa na derivative ya bidhaa ya kazi mbili

linear

maelezo ya equation tofauti ya kwanza ambayo inaweza kuandikwa kwa fomu\( a(x)y′+b(x)y=c(x)\)

fomu ya kawaida

fomu ya equation ya kwanza ya mstari tofauti iliyopatikana kwa kuandika equation tofauti katika fomu\( y'+p(x)y=q(x)\)