8.4: Mlinganyo wa vifaa

Last updated
Save as PDF

Page ID: 178685

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Eleza dhana ya uwezo wa kubeba mazingira katika mfano wa vifaa vya ukuaji wa idadi ya watu.
Chora uwanja mwelekeo kwa equation vifaa na kutafsiri curves ufumbuzi.
Kutatua equation vifaa na kutafsiri matokeo.

Ulinganyo tofauti unaweza kutumika kuwakilisha ukubwa wa idadi ya watu kama inatofautiana baada ya muda. Tuliona hili katika sura ya awali katika sehemu ya ukuaji wa kielelezo na kuoza, ambayo ni mfano rahisi zaidi. Mfano wa kweli zaidi unajumuisha mambo mengine yanayoathiri ukuaji wa idadi ya watu. Katika sehemu hii, sisi kujifunza vifaa tofauti equation na kuona jinsi inatumika kwa utafiti wa mienendo ya idadi ya watu katika mazingira ya biolojia.

Ukuaji wa idadi ya watu na Uwezo

Kwa mfano ukuaji wa idadi ya watu kwa kutumia equation tofauti, sisi kwanza haja ya kuanzisha baadhi ya vigezo na masharti husika. kutofautiana$t$. itawakilisha wakati. Vitengo vya muda vinaweza kuwa masaa, siku, wiki, miezi, au hata miaka. Tatizo lolote lolote linapaswa kutaja vitengo vinavyotumiwa katika tatizo hilo. Variable$P$ itawakilisha idadi ya watu. Kwa kuwa idadi ya watu inatofautiana baada ya muda, inaeleweka kuwa kazi ya muda. Kwa hiyo tunatumia nukuu$P(t)$ kwa idadi ya watu kama kazi ya wakati. Ikiwa$P(t)$ ni kazi tofauti, basi derivative ya kwanza$\frac{dP}{dt}$ inawakilisha kiwango cha instantaneous cha mabadiliko ya idadi ya watu kama kazi ya wakati.

Katika Ukuaji wa Kielelezo na Uozo, tulisoma ukuaji wa kielelezo na kuoza kwa idadi ya watu na vitu vyenye mionzi. Mfano wa kazi ya ukuaji wa kielelezo ni$P(t)=P_0e^{rt}.$ Katika kazi hii,$P(t)$ inawakilisha idadi ya watu kwa wakati$t,P_0$ inawakilisha idadi ya awali (idadi ya watu kwa wakati$t=0$), na mara kwa mara$r>0$ inaitwa kiwango cha ukuaji. Kielelezo$\PageIndex{1}$ inaonyesha grafu ya$P(t)=100e^{0.03t}$. Hapa$P_0=100$ na$r=0.03$.

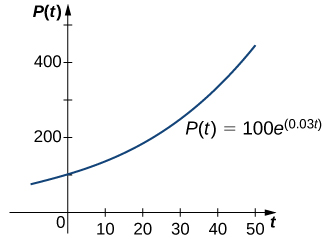
Grafu ya kazi ya kielelezo p (t) = 100 e ^ (0.03 t). Ni kuongezeka concave up kazi kuanzia katika roboduara 2, misalaba y mhimili katika (0, 100), na kuongezeka kwa roboduara 1. — Kielelezo$\PageIndex{1}$: mfano wa ukuaji wa kielelezo wa idadi ya watu.

Tunaweza kuthibitisha kwamba kazi$P(t)=P_0e^{rt}$ inatimiza tatizo la thamani ya awali

\[ \dfrac{dP}{dt}=rP \nonumber \]

na$P(0)=P_0.$

Equation hii tofauti ina tafsiri ya kuvutia. Upande wa kushoto unawakilisha kiwango ambacho idadi ya watu huongezeka (au inapungua). Upande wa mkono wa kulia ni sawa na mara kwa mara chanya inayoongezeka na idadi ya sasa. Kwa hiyo equation tofauti inasema kwamba kiwango ambacho idadi ya watu huongezeka ni sawia na idadi ya watu katika hatua hiyo kwa wakati. Zaidi ya hayo, inasema kwamba mara kwa mara ya uwiano kamwe mabadiliko.

Tatizo moja na kazi hii ni utabiri wake kwamba wakati unaendelea, idadi ya watu inakua bila kufungwa. Hii ni unrealistic katika mazingira halisi ya dunia. Sababu mbalimbali hupunguza kiwango cha ukuaji wa idadi fulani ya watu, ikiwa ni pamoja na kiwango cha kuzaliwa, kiwango cha kifo, ugavi wa chakula, wadudu, na kadhalika. Mara kwa mara ya ukuaji kwa$r$ kawaida huzingatia viwango vya kuzaliwa na vifo lakini hakuna sababu nyingine, na inaweza kutafsiriwa kama wavu (kuzaliwa bala kifo) kiwango cha ukuaji wa asilimia kwa wakati wa kitengo. Swali la asili la kuuliza ni kama kiwango cha ukuaji wa idadi ya watu kinakaa mara kwa mara, au kama kinabadilika kwa muda. Wanabiolojia wamegundua kwamba katika mifumo mingi ya kibaiolojia, idadi ya watu inakua mpaka idadi fulani ya hali ya kutosha itafikia. Uwezekano huu haukuzingatiwa na ukuaji wa kielelezo. Hata hivyo, dhana ya uwezo wa kubeba inaruhusu uwezekano kwamba katika eneo fulani, idadi fulani tu ya kiumbe au mnyama anayepewa inaweza kustawi bila kuingia katika masuala ya rasilimali.

Ufafanuzi: Uwezo wa kub

Uwezo wa kubeba wa kiumbe katika mazingira fulani hufafanuliwa kuwa idadi kubwa ya viumbe kwamba mazingira yanaweza kudumisha kwa muda usiojulikana.

Tunatumia variable$K$ ili kutaja uwezo wa kubeba. Kiwango cha ukuaji kinawakilishwa na kutofautiana$r$. Kutumia vigezo hivi, tunaweza kufafanua vifaa tofauti equation.

Ufafanuzi: Vifaa tofauti equation

Hebu$K$ kuwakilisha uwezo wa kubeba kwa viumbe fulani katika mazingira fulani, na$r$ iwe namba halisi ambayo inawakilisha kiwango cha ukuaji. Kazi$P(t)$ inawakilisha idadi ya viumbe hivi kama kazi ya wakati$t$, na mara kwa mara$P_0$ inawakilisha idadi ya awali (idadi ya viumbe kwa wakati$t=0$). Kisha vifaa tofauti equation ni

\[\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right). \label{LogisticDiffEq} \]

equation vifaa mara ya kwanza kuchapishwa na Pierre Verhulst katika$1845$. Equation hii tofauti inaweza kuunganishwa na hali ya awali$P(0)=P_0$ ili kuunda tatizo la thamani ya awali$P(t).$

Tuseme kwamba idadi ya awali ni ndogo jamaa na uwezo wa kubeba. Kisha$\frac{P}{K}$ ni ndogo, labda karibu na sifuri. Hivyo, wingi katika mabano upande wa kulia wa Equation\ ref {LogisticDifeQ} ni karibu na$1$, na upande wa kulia wa equation hii ni karibu na$rP$. Ikiwa$r>0$, basi idadi ya watu inakua kwa kasi, inayofanana na ukuaji wa kielelezo.

Hata hivyo, kama idadi ya watu inakua, uwiano$\frac{P}{K}$ pia unakua, kwa sababu$K$ ni mara kwa mara. Ikiwa idadi ya watu inabakia chini ya uwezo wa kubeba, basi$\frac{P}{K}$ ni chini ya$1$, hivyo$1−\frac{P}{K}>0$. Kwa hiyo upande wa kulia wa Equation\ ref {LogisticDifeQ} bado ni chanya, lakini wingi katika mabano hupata ndogo, na kiwango cha ukuaji hupungua kutokana. Ikiwa$P=K$ basi upande wa kulia ni sawa na sifuri, na idadi ya watu haibadilika.

Sasa tuseme kwamba idadi ya watu huanza kwa thamani ya juu kuliko uwezo wa kubeba. Kisha$\frac{P}{K}>1,$ na$1−\frac{P}{K}<0$. Kisha upande wa kulia wa Equation\ ref {LogisticDifeQ} ni hasi, na idadi ya watu hupungua. Kwa muda mrefu$P>K$, idadi ya watu hupungua. Ni kamwe kweli kufikia K kwa sababu$\frac{dP}{dt}$ kupata ndogo na ndogo, lakini idadi ya watu inakaribia uwezo wa kubeba kama$t$ mbinu infinity. Uchunguzi huu unaweza kuwakilishwa kuibua kwa njia ya mstari wa awamu. Mstari wa awamu unaelezea tabia ya jumla ya suluhisho la usawa wa tofauti wa uhuru, kulingana na hali ya awali. Kwa kesi ya uwezo wa kubeba katika usawa wa vifaa, mstari wa awamu ni kama inavyoonekana kwenye Mchoro$\PageIndex{2}$.

Mchoro wa mstari wa awamu kwa equation tofauti iliyotolewa. Mstari wa bluu wa wima na mishale kwenye mwisho wowote una alama mbili zilizowekwa alama, saa P = K na P = 0, na K — Kielelezo$\PageIndex{2}$: Mstari wa awamu kwa equation tofauti$\dfrac{dP}{dt}=rP(1−\dfrac{P}{K}).$

Mstari huu wa awamu unaonyesha kwamba wakati$P$ ni chini ya sifuri au zaidi kuliko$K$, idadi ya watu hupungua kwa muda. Wakati$P$ ni kati$0$ na$K$, idadi ya watu huongezeka baada ya muda.

Mfano$\PageIndex{1}$: Examining the Carrying Capacity of a Deer Population

Hebu fikiria idadi ya watu wa kulungu nyeupe-tailed (Odocoileus virginianus) katika hali ya Kentucky. Idara ya Kentucky ya Samaki na Rasilimali za Wanyamapori (KDFWR) huweka miongozo ya uwindaji na uvuvi Kabla ya msimu wa uwindaji wa mwaka 2004, ilikadiria idadi ya kulungu 900,000. Johnson anabainisha: “Idadi ya kulungu ambayo ina mengi ya kula na si kuwindwa na binadamu au wadudu wengine itakuwa mara mbili kila baada ya miaka mitatu.” (George Johnson, “Tatizo la Kulipuka watu wa kulungu Haina Solutions Kuvutia,” Januari 12,2001, ilifikia Aprili 9, 2015)

Hii ni picha ya kulungu. — Kielelezo$\PageIndex{3}$: (mikopo: mabadiliko ya kazi na Rachel Kramer, Flickr)

Uchunguzi huu unalingana na kiwango cha ongezeko$r=\dfrac{\ln (2)}{3}=0.2311,$ hivyo kiwango cha ukuaji wa takriban ni 23.11% kwa mwaka. (Hii inadhani kwamba idadi ya watu inakua exponentially, ambayo ni busara —angalau katika muda mfupi-na ugavi wa chakula mwingi na hakuna wadudu.) KDFWR pia inaripoti wiani wa idadi ya kulungu kwa kaunti 32 huko Kentucky, wastani wa ambayo ni takriban kulungu 27 kwa maili ya mraba. Tuseme hii ni kulungu wiani kwa hali nzima (39,732 maili mraba). Uwezo wa kubeba$K$ ni maili za mraba 39,732 mara kulungu 27 kwa maili mraba, au kulungu 1,072,764.

Kwa programu hii, tuna$P_0=900,000,K=1,072,764,$ na$r=0.2311.$ mbadala maadili haya katika Equation\ ref {LogisticDiffeQ} na kuunda tatizo awali thamani.
Tatua tatizo la thamani ya awali kutoka sehemu a.
Kwa mujibu wa mfano huu, itakuwa nini idadi ya watu katika$3$ miaka? Kumbuka kwamba muda mara mbili alitabiri na Johnson kwa idadi ya kulungu ilikuwa$3$ miaka. Je! Maadili haya yanalinganishaje?

Tuseme idadi ya watu imeweza kufikia 1,200,000 Je, usawa wa vifaa unatabiri utafanyika kwa idadi ya watu katika hali hii?

Suluhisho

a. thamani ya awali tatizo ni

\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right),\,\,P(0)=900,000. \nonumber \]

b. equation vifaa ni uhuru tofauti equation, hivyo tunaweza kutumia njia ya kujitenga ya vigezo.

Hatua ya 1: Kuweka upande wa kulia sawa na sifuri hutoa$P=0$ na$P=1,072,764.$ Hii inamaanisha kwamba ikiwa idadi ya watu itaanza saa sifuri haitabadilika kamwe, na ikiwa itaanza kwa uwezo wa kubeba, haitabadilika kamwe.

Hatua ya 2: Andika upya equation tofauti na kuzidisha pande zote mbili na:

\[ \begin{align*} \dfrac{dP}{dt} =0.2311P\left(\dfrac{1,072,764−P}{1,072,764} \right) \\[4pt] dP =0.2311P\left(\dfrac{1,072,764−P}{1,072,764}\right)dt \\[4pt] \dfrac{dP}{P(1,072,764−P)} =\dfrac{0.2311}{1,072,764}dt. \end{align*}\]

Hatua ya 3: Unganisha pande zote mbili za equation kwa kutumia sehemu ya sehemu ya kuharibika:

\[ \begin{align*} ∫\dfrac{dP}{P(1,072,764−P)} =∫\dfrac{0.2311}{1,072,764}dt \\[4pt] \dfrac{1}{1,072,764}∫ \left(\dfrac{1}{P}+\dfrac{1}{1,072,764−P}\right)dP =\dfrac{0.2311t}{1,072,764}+C \\[4pt] \dfrac{1}{1,072,764}\left(\ln |P|−\ln |1,072,764−P|\right) =\dfrac{0.2311t}{1,072,764}+C. \end{align*} \nonumber \]

Hatua ya 4: Panua pande zote mbili kwa 1,072,764 na utumie utawala wa quotient kwa logarithms:

\[\ln \left|\dfrac{P}{1,072,764−P}\right|=0.2311t+C_1. \nonumber \]

Hapa$C_1=1,072,764C.$ Next exponentiate pande zote mbili na kuondoa thamani kamili:

\[ \begin{align*} e^{\ln \left|\dfrac{P}{1,072,764−P} \right|} =e^{0.2311t + C_1} \\[4pt] \left|\dfrac{P}{1,072,764 - P}\right| =C_2e^{0.2311t} \\[4pt] \dfrac{P}{1,072,764−P} =C_2e^{0.2311t}. \end{align*}\]

Hapa$C_2=e^{C_1}$ lakini baada ya kuondoa thamani kamili, inaweza kuwa hasi pia. Sasa tatua kwa:

\[ \begin{align*} P =C_2e^{0.2311t}(1,072,764−P) \\[4pt] P =1,072,764C_2e^{0.2311t}−C_2Pe^{0.2311t} \\[4pt] P + C_2Pe^{0.2311t} = 1,072,764C_2e^{0.2311t} \\[4pt] P(1+C_2e^{0.2311t} =1,072,764C_2e^{0.2311t} \\[4pt] P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.23\nonumber11t}}. \end{align*}\]

Hatua ya 5: Kuamua thamani ya$C_2$, kwa kweli ni rahisi kurudi nyuma michache ya hatua ambapo$C_2$ ilifafanuliwa. Hasa, tumia equation

\[\dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]

Hali ya awali ni$P(0)=900,000$. Badilisha nafasi$P$$900,000$$t$ na kwa sifuri:

\[ \begin{align*} \dfrac{P}{1,072,764−P} =C_2e^{0.2311t} \\[4pt] \dfrac{900,000}{1,072,764−900,000} =C_2e^{0.2311(0)} \\[4pt] \dfrac{900,000}{172,764} =C_2 \\[4pt] C_2 =\dfrac{25,000}{4,799} \\[4pt] ≈5.209. \end{align*}\]

Kwa hiyo

\[ \begin{align*} P(t) =\dfrac{1,072,764 \left(\dfrac{25000}{4799}\right)e^{0.2311t}}{1+(250004799)e^{0.2311t}}\\[4pt] =\dfrac{1,072,764(25000)e^{0.2311t}}{4799+25000e^{0.2311t}.} \end{align*}\]

Kugawanya nambari na denominator kwa 25,000 inatoa

\[P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]

Kielelezo ni grafu ya equation hii.

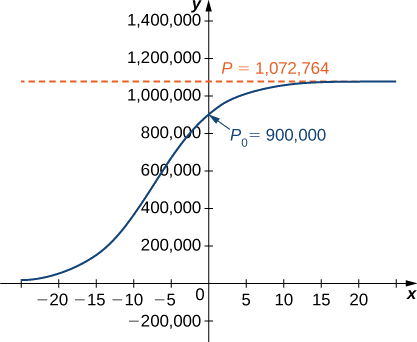
Grafu ya Curve ya vifaa kwa idadi ya watu wa kulungu na idadi ya awali ya P_0 ya 900,000. Grafu huanza kama kuongezeka concave up kazi katika roboduara mbili, mabadiliko ya kuongezeka concave chini kazi, misalaba x mhimili katika (0, 900,000), na asymptotically inakaribia P = 1,072,764 kama x inakwenda infinity. — Kielelezo$\PageIndex{4}$: Vifaa Curve kwa idadi ya kulungu na idadi ya awali ya **900,000** kulungu.

c Kutumia mfano huu tunaweza kutabiri idadi ya watu katika miaka 3.

\[P(3)=\dfrac{1,072,764e^{0.2311(3)}}{0.19196+e^{0.2311(3)}}≈978,830\,deer \nonumber \]

Hii ni mbali mfupi wa mara mbili idadi ya awali ya$900,000.$ Kumbuka kwamba mara mbili ni msingi wa dhana kwamba kiwango cha ukuaji kamwe mabadiliko, lakini mfano vifaa inachukua uwezekano huu katika akaunti.

d Kama idadi ya watu kufikiwa kulungu 1,200,000, basi mpya ya awali ya thamani tatizo itakuwa

\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right), \, P(0)=1,200,000. \nonumber \]

Suluhisho la jumla la equation tofauti lingebaki sawa.

\[ P(t)=\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \nonumber \]

Kuamua thamani ya mara kwa mara, kurudi kwenye equation

\[ \dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]

Kubadilisha maadili$t=0$ na$P=1,200,000,$ unapata

\[ \begin{align*} C_2e^{0.2311(0)} =\dfrac{1,200,000}{1,072,764−1,200,000} \\[4pt] C_2 =−\dfrac{100,000}{10,603}≈−9.431.\end{align*}\]

Kwa hiyo

\[ \begin{align*} P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \\[4pt] =\dfrac{1,072,764 \left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}}{1+\left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}} \\[4pt] =−\dfrac{107,276,400,000e^{0.2311t}}{100,000e^{0.2311t}−10,603} \\[4pt] ≈\dfrac{10,117,551e^{0.2311t}}{9.43129e^{0.2311t}−1} \end{align*}\]

equation Hii ni graphid katika Kielelezo$\PageIndex{5}$.

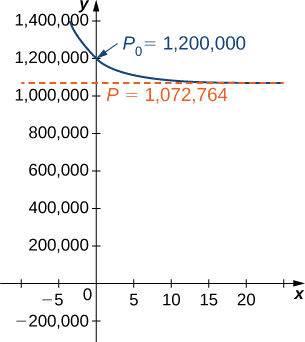
Grafu ya curve ya vifaa kwa idadi ya awali ya kulungu 1,200,000. Grafu ni kupungua concave up kazi ambayo huanza katika roboduara mbili, misalaba y mhimili katika (0, 1,200,000), na asymptotically inakaribia P = 1,072,764 kama x inakwenda infinity. — Kielelezo$\PageIndex{5}$: Curve ya vifaa kwa idadi ya watu wa kulungu na idadi ya awali ya kulungu **1,200,000**.

Kutatua equation tofauti ya vifaa

vifaa tofauti equation ni uhuru tofauti equation, hivyo tunaweza kutumia mgawanyo wa vigezo kupata ufumbuzi wa jumla, kama sisi tu alifanya katika Mfano$\PageIndex{1}$.

Hatua ya 1: Kuweka upande wa kulia sawa na sifuri husababisha$P=0$ na$P=K$ kama ufumbuzi wa mara kwa mara. Suluhisho la kwanza linaonyesha kwamba wakati hakuna viumbe vilivyopo, idadi ya watu haitakua kamwe. Suluhisho la pili linaonyesha kwamba wakati idadi ya watu inapoanza uwezo wa kubeba, haitabadilika kamwe.

Hatua ya 2: Andika upya equation tofauti katika fomu

\[ \dfrac{dP}{dt}=\dfrac{rP(K−P)}{K}. \nonumber \]

Kisha kuzidisha pande zote mbili$dt$ na kugawanya pande zote mbili na$P(K−P).$ Hii inasababisha

\[ \dfrac{dP}{P(K−P)}=\dfrac{r}{K}dt. \nonumber \]

Kuzidisha pande zote mbili za equation$K$ na kuunganisha:

\[ ∫\dfrac{K}{P(K−P)}dP=∫rdt. \label{eq20a} \]

Upande wa kushoto wa equation hii unaweza kuunganishwa kwa kutumia sehemu ya utengano wa sehemu. Tunakuacha ili uhakikishe kwamba

\[ \dfrac{K}{P(K−P)}=\dfrac{1}{P}+\dfrac{1}{K−P}. \nonumber \]

Kisha equation\ ref {eq20a} inakuwa

\[ ∫\dfrac{1}{P}+\dfrac{1}{K−P}dP=∫rdt \nonumber \]

\[ \ln |P|−\ln |K−P|=rt+C \nonumber \]

\[ \ln ∣\dfrac{P}{K−P}∣=rt+C. \nonumber \]

Sasa exponentiate pande zote mbili za equation kuondoa logarithm asili:

\[ e^{\ln ∣\dfrac{P}{K−P}∣}=e^{rt+C} \nonumber \]

\[ ∣\dfrac{P}{K−P}∣=e^Ce^{rt}. \nonumber \]

Sisi kufafanua$C_1=e^c$ ili equation inakuwa

\[ \dfrac{P}{K−P}=C_1e^{rt}. \label{eq30a} \]

Ili kutatua equation hii kwa$P(t)$, kwanza kuzidisha pande zote mbili$K−P$ na kukusanya maneno zenye$P$ upande wa kushoto wa equation:

\[\begin{align*} P =C_1e^{rt}(K−P) \\[4pt] =C_1Ke^{rt}−C_1Pe^{rt} \\[4pt] P+C_1Pe^{rt} =C_1Ke^{rt}.\end{align*}\]

Kisha, fikiria$P$ kutoka upande wa kushoto na ugawanye pande zote mbili kwa sababu nyingine:

\[\begin{align*} P(1+C_1e^{rt}) =C_1Ke^{rt} \\[4pt] P(t) =\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}. \end{align*}\]

Hatua ya mwisho ni kuamua thamani ya Njia rahisi$C_1.$ ya kufanya hivyo ni kubadilisha$t=0$ na badala ya$P_0$$P$ katika Equation na kutatua kwa$C_1$:

\[\begin{align*} \dfrac{P}{K−P} = C_1e^{rt} \\[4pt] \dfrac{P_0}{K−P_0} =C_1e^{r(0)} \\[4pt] C_1 = \dfrac{P_0}{K−P_0}. \end{align*}\]

Hatimaye, badala ya kujieleza kwa$C_1$ katika Equation\ ref {eq30a}:

\[ P(t)=\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}=\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \nonumber \]

Sasa kuzidisha nambari na denominator ya upande wa kulia$(K−P_0)$ na kurahisisha:

\[\begin{align*} P(t) =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \\[4pt] =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}}⋅\dfrac{K−P_0}{K−P_0} =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}. \end{align*}\]

Tunasema matokeo haya kama theorem.

Suluhisho la Equation tofauti ya Vifaa

Fikiria vifaa tofauti equation chini ya idadi ya awali ya$P_0$ na uwezo wa kubeba$K$ na kiwango cha ukuaji$r$. Suluhisho la tatizo la thamani ya awali linatolewa na

\[P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \nonumber \].

Sasa kwa kuwa tuna suluhisho la tatizo la thamani ya awali, tunaweza kuchagua maadili$P_0,r$,$K$ na kujifunza ufumbuzi wa ufumbuzi. Kwa mfano, katika Mfano tulitumia maadili$r=0.2311,K=1,072,764,$ na idadi ya awali ya$900,000$ kulungu. Hii inasababisha ufumbuzi

\[\begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{(1,072,764−900,000)+900,000e^{0.2311t}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{172,764+900,000e^{0.2311t}}.\end{align*}\]

Kugawanya juu na chini kwa$900,000$ anatoa

\[ P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]

Hii ni sawa na ufumbuzi wa awali. Grafu ya ufumbuzi huu inavyoonekana tena katika bluu katika Kielelezo$\PageIndex{6}$, juu ya grafu ya mfano wa ukuaji wa kielelezo na idadi ya awali$900,000$ na kiwango cha ukuaji$0.2311$ (kuonekana katika kijani). Mstari uliopigwa nyekundu unawakilisha uwezo wa kubeba, na ni asymptote ya usawa wa suluhisho la equation ya vifaa.

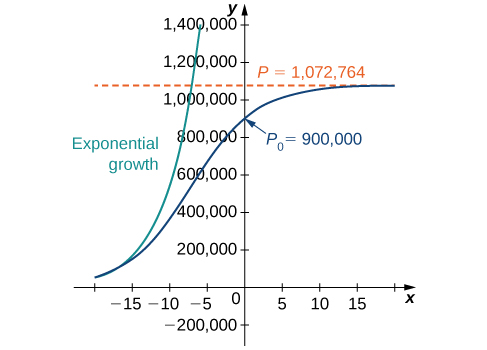
Grafu inayoonyesha ukuaji wa kielelezo na vifaa kwa idadi sawa ya awali ya viumbe 900,000 na kiwango cha ukuaji wa 23.11%. Wote kuanza katika roboduara mbili karibu na mhimili x kama kuongeza concave up curves. Curve ya ukuaji wa kielelezo inaendelea kukua, kupita P = 1,072,764 wakati bado katika roboduara mbili. Curve ya ukuaji wa vifaa hubadilika concavity, huvuka mhimili x saa P_0 = 900,000, na kwa njia isiyo ya kawaida inakaribia P = 1,072,764. — Kielelezo$\PageIndex{6}$: kulinganisha kielelezo dhidi ya ukuaji wa vifaa kwa idadi hiyo ya awali ya$900,000$ viumbe na kiwango cha ukuaji wa$23.11%.$

Kufanya kazi chini ya dhana kwamba idadi ya watu inakua kulingana na equation tofauti ya vifaa, grafu hii inabiri kwamba takriban$20$ miaka mapema$(1984)$, ukuaji wa idadi ya watu ulikuwa karibu sana na kielelezo. Kiwango cha ukuaji halisi wakati huo ingekuwa karibu$23.1%$ kwa mwaka. Kama muda unaendelea, grafu mbili tofauti. Hii hutokea kwa sababu idadi ya watu huongezeka, na equation tofauti ya vifaa inasema kuwa kiwango cha ukuaji hupungua kadiri idadi ya watu inavyoongezeka. Wakati idadi ya watu ilipimwa$(2004)$, ilikuwa karibu na uwezo wa kubeba, na idadi ya watu ilianza kufikia ngazi.

Suluhisho la equation tofauti ya vifaa ina hatua ya kufuta. Ili kupata hatua hii, weka derivative ya pili sawa na sifuri:

\[ \begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \\[4pt] P′(t) =\dfrac{rP_0K(K−P0)e^{rt}}{((K−P_0)+P_0e^{rt})^2} \\[4pt] P''(t) =\dfrac{r^2P_0K(K−P_0)^2e^{rt}−r^2P_0^2K(K−P_0)e^{2rt}}{((K−P_0)+P_0e^{rt})^3} \\[4pt] =\dfrac{r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})}{((K−P_0)+P_0e^{rt})^3}. \end{align*}\]

Kuweka namba sawa na sifuri,

\[ r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})=0. \nonumber \]

Muda mrefu kama$P_0≠K$, kiasi nzima kabla na ikiwa$e^{rt}$ ni pamoja na nonzero, hivyo tunaweza kugawanya nje:

\[ (K−P_0)−P_0e^{rt}=0. \nonumber \]

Kutatua kwa$t$,

\[ P_0e^{rt}=K−P_0 \nonumber \]

\[ e^{rt}=\dfrac{K−P_0}{P_0} \nonumber \]

\[ \ln e^{rt}=\ln \dfrac{K−P_0}{P_0} \nonumber \]

\[ rt=\ln \dfrac{K−P_0}{P_0} \nonumber \]

\[ t=\dfrac{1}{r}\ln \dfrac{K−P_0}{P_0}. \nonumber \]

Angalia kwamba ikiwa$P_0>K$, basi kiasi hiki hakijulikani, na grafu haina uhakika wa kufuta. Katika grafu ya vifaa, hatua ya kufuta inaweza kuonekana kama hatua ambapo grafu inabadilika kutoka concave hadi concave chini. Hii ndio ambapo “kiwango cha mbali” kinaanza kutokea, kwa sababu kiwango cha ukuaji wa wavu kinakuwa polepole kadiri idadi ya watu inapoanza kufikia uwezo wa kubeba.

Zoezi$\PageIndex{1}$

Idadi ya sungura katika meadow inaonekana kuwa$200$ sungura kwa wakati$t=0$. Baada ya mwezi, idadi ya sungura inazingatiwa kuwa imeongezeka kwa$4%$. Kwa kutumia idadi ya awali ya$200$ na kiwango cha ukuaji wa$0.04$, na uwezo wa kubeba ya$750$ sungura,

Andika vifaa tofauti equation na hali ya awali kwa mfano huu.
Chora uwanja mteremko kwa equation hii vifaa tofauti, na mchoro ufumbuzi sambamba na idadi ya awali ya$200$ sungura.
Tatua tatizo la thamani ya awali kwa$P(t)$.
Tumia ufumbuzi wa kutabiri idadi ya watu baada ya$1$ mwaka.

Kidokezo: Kwanza kuamua maadili ya$r,K,$ na$P_0$. Kisha uunda tatizo la thamani ya awali, futa uwanja wa mwelekeo, na usuluhishe tatizo.

Jibu

a.$\dfrac{dP}{dt}=0.04(1−\dfrac{P}{750}),P(0)=200$

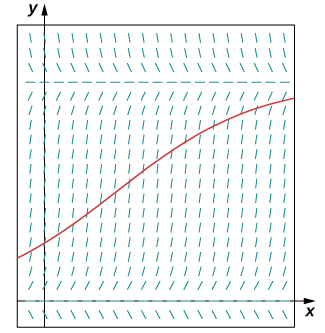
$Shamba la mwelekeo na mistari ya usawa kwenye mhimili x na y = 15. Mstari mwingine ni wima, isipokuwa kwa wale wanaojitokeza kwenye mhimili x na y = 15. Suluhisho hutolewa ambayo huvuka mhimili y karibu (0, 4) na mbinu zisizo za kawaida y = 15.$

c.$P(t)=\dfrac{3000e^{.04t}}{11+4e^{.04t}}$

d Baada ya$12$ miezi, idadi ya watu watakuwa$P(12)≈278$ sungura.

Mradi wa Wanafunzi: Mlinganyo wa vifaa na Idadi ya Watu

Uboreshaji wa mfano wa vifaa ni pamoja na idadi ya kizingiti. Idadi ya kizingiti hufafanuliwa kuwa idadi ya chini ambayo ni muhimu kwa spishi kuishi. Tunatumia variable$T$ kuwakilisha idadi ya kizingiti. Equation tofauti ambayo inashirikisha idadi ya kizingiti$T$ na uwezo wa kubeba$K$ ni

\[ \dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right) \nonumber \]

ambapo$r$ inawakilisha kiwango cha ukuaji, kama kabla.

Idadi ya kizingiti ni muhimu kwa wanabiolojia na inaweza kutumika ili kuamua kama aina fulani inapaswa kuwekwa kwenye orodha iliyohatarishwa. Kikundi cha watafiti wa Australia wanasema wameamua idadi ya kizingiti kwa aina yoyote ya kuishi:$5000$ watu wazima. (Catherine Claby, “Idadi Magic,” American Scientist 98 (1): 24, doi:10.1511/2010.82.24. kupatikana Aprili 9, 2015, www.americanscientist.org/iss... -magic-nambari). Kwa hiyo tunatumia$T=5000$ kama idadi ya kizingiti katika mradi huu. Tuseme kwamba uwezo wa kubeba mazingira katika Montana kwa elk ni$25,000$. Weka Equation kutumia uwezo wa kubeba$25,000$ na kizingiti idadi ya$5000$. Kudhani kila mwaka wavu kiwango cha ukuaji wa 18%.
Chora uwanja wa mwelekeo kwa usawa tofauti kutoka hatua$1$, pamoja na ufumbuzi kadhaa kwa idadi tofauti ya awali. Je, ni ufumbuzi wa mara kwa mara wa equation tofauti? Je, ufumbuzi huu unahusiana na mfano wa awali wa idadi ya watu (yaani, katika mazingira ya kibiolojia)?
Idadi ya watu kikwazo ni nini kwa kila idadi ya awali uliyochagua kwa hatua$2$? (Kidokezo: tumia shamba la mteremko ili uone kinachotokea kwa wakazi mbalimbali wa awali, yaani, angalia asymptotes ya usawa ya ufumbuzi wako.)
Equation hii inaweza kutatuliwa kwa kutumia njia ya kujitenga kwa vigezo. Hata hivyo, ni vigumu sana kupata ufumbuzi kama kazi wazi ya$t$. Kutumia idadi ya awali ya$18,000$ elk, kutatua tatizo la thamani ya awali na ueleze suluhisho kama kazi thabiti ya t, au kutatua tatizo la jumla la thamani ya awali, kutafuta suluhisho kwa suala la$r,K,T,$ na$P_0$.

Dhana muhimu

Wakati wa kusoma kazi za idadi ya watu, dhana tofauti-kama ukuaji wa kielelezo, ukuaji wa vifaa, au idadi ya watu wa kizingiti husababisha viwango tofauti vya ukuaji.
Equation tofauti ya vifaa inashirikisha dhana ya uwezo wa kubeba. Thamani hii ni thamani ya kupunguza kwa idadi ya watu kwa mazingira yoyote.
Equation tofauti ya vifaa inaweza kutatuliwa kwa kiwango chochote cha ukuaji chanya, idadi ya awali, na uwezo wa kubeba.

Mlinganyo muhimu

Vifaa tofauti vya usawa na tatizo la thamani ya awali

$\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right),\quad P(0)=P_0$

Suluhisho la tatizo la usawa wa tofauti/thamani ya awali

$P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}$

Kizingiti idadi ya watu mfano

$\dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right)$

faharasa

uwezo wa kubeba: idadi ya watu upeo wa viumbe kwamba mazingira yanaweza kuendeleza kwa muda usiojulikana

kiwango cha ukuaji: mara kwa mara$r>0$ katika kazi ya ukuaji wa kielelezo$P(t)=P_0e^{rt}$

idadi ya awali: idadi ya watu kwa wakati$t=0$

vifaa tofauti equation: equation tofauti ambayo inashirikisha uwezo wa kubeba$K$ na kiwango cha ukuaji rr katika mfano wa idadi ya watu

mstari wa awamu: uwakilishi wa kuona wa tabia ya ufumbuzi wa usawa wa tofauti wa uhuru chini ya hali mbalimbali za awali

kizingiti idadi: kiwango cha chini cha idadi ya watu kwamba ni muhimu kwa ajili ya aina ya kuishi

Ufafanuzi: Uwezo wa kub

Ufafanuzi: Vifaa tofauti equation

Mfano\(\PageIndex{1}\): Examining the Carrying Capacity of a Deer Population

Suluhisho la Equation tofauti ya Vifaa

Zoezi\(\PageIndex{1}\)

Mradi wa Wanafunzi: Mlinganyo wa vifaa na Idadi ya Watu