8.3: Equations inayoweza kutenganishwa

Malengo ya kujifunza

• Tumia mgawanyo wa vigezo ili kutatua equation tofauti.
• Tatua programu kwa kutumia kujitenga kwa vigezo.

Sasa tunachunguza mbinu ya ufumbuzi kwa ajili ya kutafuta ufumbuzi halisi kwa darasa la equations tofauti inayojulikana kama equations tofauti tofauti. Ulinganyo huu ni wa kawaida katika taaluma mbalimbali, ikiwa ni pamoja na fizikia, kemia, na uhandisi. Tunaonyesha maombi machache mwishoni mwa sehemu.

Kugawanyika kwa Vigezo

Tunaanza na ufafanuzi na baadhi ya mifano.

Ufafanuzi: Mlinganyo wa kutofautiana

Equation tofauti tofauti ni equation yoyote ambayo inaweza kuandikwa kwa fomu

$$y'=f(x)g(y). \label{sep}$$

Neno 'kutenganishwa' linamaanisha ukweli kwamba upande wa kulia wa Equation\ ref {sep} inaweza kutengwa katika kazi ya$x$ nyakati kazi ya$y$. Mifano ya equations tofauti tofauti ni pamoja na

$$\begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align}$$

Equation\ ref {eq2} inatenganishwa$f(x)=6x^2+4x$ na$g(y)=1$, Equation\ ref {eq3} inatenganishwa$f(x)=1$$g(y)=\sec y+\tan y,$ na na na upande wa kulia wa Equation\ ref {eq4} unaweza$(x+3)(y−2)$ kuhesabiwa kama, hivyo ni kutenganishwa pia. Equation\ ref {eq3} pia huitwa equation tofauti ya uhuru kwa sababu upande wa kulia wa equation ni kazi ya$y$ pekee. Ikiwa equation tofauti inatenganishwa, basi inawezekana kutatua equation kwa kutumia njia ya kujitenga kwa vigezo.

Mkakati wa Kutatua matatizo: Kugawanyika kwa Vigezo

1. Angalia kwa maadili yoyote ya$y$ kwamba kufanya$g(y)=0.$ Hizi yanahusiana na ufumbuzi wa mara kwa mara.
2. Andika upya equation tofauti katika fomu $$\dfrac{dy}{g(y)}=f(x)dx. \nonumber$$
3. Unganisha pande zote mbili za equation.
4. Kutatua equation kusababisha$y$ kama inawezekana.
5. Kama hali ya awali ipo, badala maadili sahihi kwa$x$ na$y$ katika equation na kutatua kwa mara kwa mara.

Kumbuka kuwa Hatua ya 4 inasema “Tatua usawa$y$ unaosababisha iwezekanavyo.” Si mara zote inawezekana kupata$y$ kama kazi wazi ya$x$. Mara nyingi tunapaswa kuridhika na kutafuta y kama kazi thabiti ya$x$.

Mfano$\PageIndex{1}$: Using Separation of Variables

Pata suluhisho la jumla kwa equation tofauti$y'=(x^2−4)(3y+2)$ kwa kutumia njia ya kujitenga kwa vigezo.

Suluhisho

Fuata njia ya hatua tano ya kujitenga kwa vigezo.

1. Katika mfano huu,$f(x)=x^2−4$ na$g(y)=3y+2$. Kuweka$g(y)=0$ hutoa$y=−\dfrac{2}{3}$ kama suluhisho la mara kwa mara.

2. Andika upya equation tofauti katika fomu

$$\dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber$$

3. Unganisha pande zote mbili za equation:

$$∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber$$

Hebu$u=3y+2$. Kisha$du=3\dfrac{dy}{dx}\,dx$, hivyo equation inakuwa

$$\dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber$$

$$\dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber$$

$$\dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber$$

4. Ili kutatua equation hii kwa$y$, kwanza kuzidisha pande zote mbili za equation na$3$.

$$\ln|3y+2|=x^3−12x+3C\nonumber$$

Sasa tunatumia mantiki fulani katika kushughulika na mara kwa mara$C$. Tangu$C$ inawakilisha mara kwa mara ya kiholela,$3C$ pia inawakilisha mara kwa mara. Ikiwa tunaita mara kwa mara ya pili ya kiholela$C_1,$ ambapo$C_1 = 3C,$ equation inakuwa

$$\ln|3y+2|=x^3−12x+C_1.\nonumber$$

Sasa exponentiate pande zote mbili za equation (yaani, kufanya kila upande wa equation exponent kwa msingi$e$).

$$\begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}$$

Tena kufafanua mara kwa mara mpya$C_2= e^{C_1}$ (kumbuka kuwa$C_2 > 0$):

$$|3y+2|=C_2e^{x^3−12x}.\nonumber$$

Kwa sababu ya thamani kamili upande wa kushoto wa equation, hii inalingana na equations mbili tofauti:

$$3y+2=C_2e^{x^3−12x}\nonumber$$

na

$$3y+2=−C_2e^{x^3−12x}.\nonumber$$

Suluhisho la equation ama linaweza kuandikwa kwa fomu

$$y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber$$

Kwa kuwa$C_2>0$, haijalishi kama tunatumia plus au minus, hivyo mara kwa mara anaweza kuwa na ishara ama. Zaidi ya hayo, subscript juu ya mara kwa mara$C$ ni kabisa holela, na inaweza kuwa imeshuka. Kwa hiyo, ufumbuzi unaweza kuandikwa kama

$$y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber$$

Kumbuka kuwa kwa kuandika suluhisho moja kwa ujumla kwa njia hii, sisi pia$C$ tunaruhusu sawa$0$. Hii inatupa ufumbuzi umoja,$y = -\dfrac{2}{3}$, kwa equation tofauti iliyotolewa. Angalia kwamba hii ni kweli suluhisho la equation hii tofauti!

5. Hakuna hali ya awali iliyowekwa, kwa hiyo tumekamilika.

Zoezi$\PageIndex{1}$

Tumia njia ya kujitenga kwa vigezo ili kupata suluhisho la jumla kwa usawa tofauti

$$y'=2xy+3y−4x−6. \nonumber$$

Kidokezo

Sababu ya kwanza upande wa kulia wa equation kwa kikundi, kisha utumie mkakati wa hatua tano wa kujitenga kwa vigezo.

Jibu

$$y=2+Ce^{x^2+3x} \nonumber$$

Mfano$\PageIndex{2}$: Solving an Initial-Value Problem

Kutumia njia ya kujitenga kwa vigezo, tatua tatizo la thamani ya awali

$$y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber$$

Suluhisho

Fuata njia ya hatua tano ya kujitenga kwa vigezo.

1. Katika mfano huu,$f(x)=2x+3$ na$g(y)=y^2−4$. Kuweka$g(y)=0$ hutoa$y=±2$ kama ufumbuzi wa mara kwa mara.

2. Gawanya pande zote mbili za equation$y^2−4$ na kuzidisha na$dx$. Hii inatoa equation

$$\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber$$

3. Ifuatayo kuunganisha pande zote mbili:

$$∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2}$$

Ili kutathmini upande wa kushoto, tumia njia ya uharibifu wa sehemu ya sehemu. Hii inasababisha utambulisho

$$\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber$$

Kisha Equation\ ref {Ex2.2} inakuwa

$$\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber$$

$$\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber$$

Kuzidisha pande zote mbili za equation hii na$4$ na kuchukua nafasi$4C$ na$C_1$ anatoa

$$\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber$$

$$\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber$$

4. Inawezekana kutatua equation hii kwa$y.$ Kwanza exponentiate pande zote mbili za equation na kufafanua$C_2=e^{C_1}$:

$$\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber$$

Halafu tunaweza kuondoa thamani kamili na kuruhusu mara kwa mara mpya$C_3$ kuwa chanya, hasi, au sifuri, yaani,$C_3 =\pm C_2$ au$C_3 = 0.$

Kisha kuzidisha pande zote mbili na$y+2$.

$$y−2=C_3(y+2)e^{4x^2+12x}\nonumber$$

$$y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber$$

Sasa kukusanya masharti yote kuwashirikisha$y$ upande mmoja wa equation, na kutatua kwa$y$:

$$y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber$$

$$y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber$$

$$y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber$$

5. Kuamua thamani ya$C_3$, mbadala$x=0$ na$y=−1$ katika suluhisho la jumla. Vinginevyo, tunaweza kuweka maadili sawa katika equation mapema, yaani equation$\dfrac{y−2}{y+2}=C_3e^{4x^2+12}$. Hii ni rahisi sana kutatua kwa$C_3$:

$$\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber$$

$$\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber$$

$$C_3=−3.\nonumber$$

Kwa hiyo, suluhisho la tatizo la thamani ya awali ni

$$y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber$$

Grafu ya suluhisho hili inaonekana kwenye Kielelezo$\PageIndex{1}$.

Kielelezo$\PageIndex{1}$: Grafu ya suluhisho la tatizo la thamani ya awali$y'=(2x+3)(y^2−4),y(0)=−1$.

Zoezi$\PageIndex{2}$

Pata suluhisho la tatizo la thamani ya awali

$$6y'=(2x+1)(y^2−2y−8) \nonumber$$

kwa$y(0)=−3$ kutumia njia ya kujitenga kwa vigezo.

Kidokezo

Fuata hatua za kujitenga kwa vigezo ili kutatua tatizo la thamani ya awali.

Jibu

$$y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber$$

Matumizi ya Kugawanyika kwa Vigezo

Matatizo mengi ya kuvutia yanaweza kuelezewa na equations inayoweza kutenganishwa. Tunaonyesha aina mbili za matatizo: viwango vya ufumbuzi na sheria ya Newton ya baridi.

Suluhisho viwango

Fikiria tank kujazwa na suluhisho la chumvi. Tungependa kuamua kiasi cha chumvi kilichopo kwenye tangi kama kazi ya muda. Tunaweza kutumia mchakato wa kujitenga kwa vigezo kutatua tatizo hili na matatizo kama hayo yanayohusisha viwango vya ufumbuzi.

Mfano$\PageIndex{3}$: Determining Salt Concentration over Time

Tangi iliyo na$100$ L ya suluhisho la brine awali ina$4$ kilo cha chumvi kilichopasuka katika suluhisho. Kwa wakati$t=0$, suluhisho lingine la brine linaingia ndani ya tangi kwa kiwango cha$2$ L/min. Suluhisho hili la brine lina mkusanyiko wa$0.5$ kg/L ya chumvi. Wakati huo huo, stopcock inafunguliwa chini ya tank, kuruhusu suluhisho la pamoja linapita kwa kiwango cha$2$ L/min, ili kiwango cha kioevu katika tank kinabaki mara kwa mara (Kielelezo$\PageIndex{2}$). Kupata kiasi cha chumvi katika tank kama kazi ya muda (kipimo kwa dakika), na kupata kiasi kikubwa cha chumvi katika tank, kuchukua kwamba ufumbuzi katika tank ni vizuri mchanganyiko wakati wote.

Kielelezo$\PageIndex{2}$: Tangi ya brine yenye kiasi cha awali cha suluhisho la chumvi inakubali mtiririko wa pembejeo na hutoa mtiririko wa pato. Je! Kiasi cha chumvi kinabadilikaje na wakati?

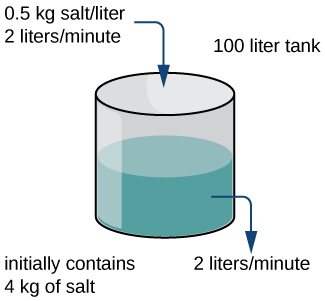
Suluhisho

Kwanza tunafafanua kazi$u(t)$ ambayo inawakilisha kiasi cha chumvi kwa kilo katika tangi kama kazi ya wakati. Kisha$\dfrac{du}{dt}$ inawakilisha kiwango ambacho kiasi cha chumvi katika tangi kinabadilika kama kazi ya muda. Pia,$u(0)$ inawakilisha kiasi cha chumvi katika tangi kwa wakati$t=0$, ambayo ni$4$ kilo.

Kuanzisha jumla kwa equation tofauti tutakayotatua ni ya fomu

$$\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber$$

RATE YA UINGIZAJI inawakilisha kiwango ambacho chumvi huingia kwenye tangi, na OUTFLOW RATE inawakilisha kiwango ambacho chumvi huacha tank. Kwa sababu suluhisho huingia kwenye tangi kwa kiwango cha$2$ L/min, na lita moja ya suluhisho ina$0.5$ kilo cha chumvi, kila$2(0.5)=1$ kilo cha chumvi huingia kwenye tangi. Kwa hiyo uingiaji RATE =$1$.

Ili kuhesabu kiwango ambacho chumvi huacha tank, tunahitaji mkusanyiko wa chumvi kwenye tangi wakati wowote kwa wakati. Kwa kuwa kiasi halisi cha chumvi kinatofautiana kwa muda, ndivyo mkusanyiko wa chumvi. Hata hivyo, kiasi cha suluhisho kinaendelea kudumu kwa lita 100. Idadi ya kilo ya chumvi katika tangi kwa wakati$t$ ni sawa na$u(t)$. Hivyo, mkusanyiko wa chumvi ni$\dfrac{u(t)}{100}$ kg/L, na suluhisho linaacha tank kwa kiwango cha$2$ L/min. Kwa hiyo chumvi huacha tank kwa kiwango cha$\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}$ kilo/min, na OUTFLOW RATE ni sawa na$\dfrac{u(t)}{50}$. Kwa hiyo equation tofauti inakuwa$\dfrac{du}{dt}=1−\dfrac{u}{50}$, na hali$u(0)=4.$ ya awali ni. awali thamani tatizo kutatuliwa ni

$$\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber$$

equation tofauti ni equation kujitenga, hivyo tunaweza kutumia mkakati wa hatua tano kwa ajili ya ufumbuzi.

Hatua ya 1. Kuweka$1−\dfrac{u}{50}=0$ hutoa$u=50$ kama suluhisho la mara kwa mara. Kwa kuwa kiasi cha awali cha chumvi katika tangi ni$4$ kilo, suluhisho hili halitumiki.

Hatua ya 2. Andika upya equation kama

$$\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber$$

Kisha kuzidisha pande zote mbili$dt$ na kugawanya pande zote mbili$50−u:$

$$\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber$$

Hatua ya 3. Unganisha pande zote mbili:

$$\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}$$

Hatua ya 4. Tatua kwa$u(t)$:

$$\ln|50−u|=−\dfrac{t}{50}−C\nonumber$$

$$e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber$$

$$|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber$$

Ondoa thamani kamili kwa kuruhusu mara kwa mara kuwa chanya, hasi, au sifuri, yaani,$C_1 = \pm e^{-C}$ au$C_1 = 0$:

$$50−u=C_1e^{−t/50}.\nonumber$$

Hatimaye, tatua kwa$u(t)$:

$$u(t)=50−C_1e^{−t/50}.\nonumber$$

Hatua ya 5. Tatua kwa$C_1$:

$$\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}$$

Suluhisho la tatizo la thamani ya awali ni$u(t)=50−46e^{−t/50}.$ Kupata kiasi kikubwa cha chumvi katika tangi, chukua kikomo kama$t$ mbinu infinity:

$$\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}$$

Kumbuka kwamba hii ilikuwa suluhisho la mara kwa mara kwa usawa tofauti. Ikiwa kiasi cha awali cha chumvi katika tangi ni$50$ kilo, basi inabakia mara kwa mara. Ikiwa huanza chini ya$50$ kilo, basi inakaribia$50$ kilo kwa muda.

Zoezi$\PageIndex{3}$

Tangi ina$3$ kilo cha chumvi kilichopasuka katika$75$ lita za maji. Suluhisho la chumvi la chumvi la$0.4$ kilo/L hupigwa ndani ya tangi kwa kiwango cha$6$ L/min na hutolewa kwa kiwango sawa. Tatua kwa mkusanyiko wa chumvi kwa wakati$t$. Fikiria tank imechanganywa vizuri wakati wote.

Kidokezo

Fuata hatua katika Mfano$\PageIndex{3}$ na ueleze kujieleza kwa uingizaji na OUTFLOW. Kuunda tatizo la thamani ya awali, na kisha uitatua.

Tatizo la thamani ya awali:

$$\dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber$$

Jibu

$$u(t)=30−27e^{−t/50} \nonumber$$

Sheria ya Newton ya Baridi

Sheria ya Newton ya baridi inasema kwamba kiwango cha mabadiliko ya halijoto ya kitu ni sawia na tofauti kati ya halijoto lake mwenyewe na halijoto iliyoko (yaani, halijoto ya mazingira yake). Ikiwa tunaruhusu$T(t)$ kuwakilisha joto la kitu kama kazi ya wakati, basi$\dfrac{dT}{dt}$ inawakilisha kiwango ambacho joto hilo linabadilika. Joto la mazingira ya kitu linaweza kuwakilishwa na$T_s$. Kisha sheria ya Newton ya baridi inaweza kuandikwa kwa fomu

$$\dfrac{dT}{dt}=k(T(t)−T_s) \nonumber$$

au tu

$$\dfrac{dT}{dt}=k(T−T_s). \nonumber$$

Joto la kitu mwanzoni mwa jaribio lolote ni thamani ya awali kwa tatizo la thamani ya awali. Tunaita joto hili$T_0$. Kwa hiyo, tatizo la thamani ya awali ambalo linahitaji kutatuliwa linachukua fomu

$$\dfrac{dT}{dt}=k(T−T_s) \label{newton}$$

na$T(0)=T_0$,$k$ wapi mara kwa mara ambayo inahitaji kutolewa au kuamua katika mazingira ya tatizo. Tunatumia equations hizi katika Mfano$\PageIndex{4}$.

Mfano$\PageIndex{4}$: Waiting for a Pizza to Cool

Pizza huondolewa kwenye tanuri baada ya kuoka vizuri, na joto la tanuri ni Joto$350°F.$ la jikoni ni$75°F$, na baada ya$5$ dakika joto la pizza ni$340°F$. Tungependa kusubiri mpaka joto la pizza lifikia$300°F$ kabla ya kukata na kuitumikia (Kielelezo$\PageIndex{3}$). Je! Tutahitaji kusubiri muda gani?

Kielelezo$\PageIndex{3}$: Kutoka sheria ya Newton ya baridi, ikiwa pizza hupungua$10°F$ kwa$5$ dakika, ni muda gani kabla ya kupungua$300°F$?

Suluhisho

Joto la kawaida (joto la jirani) ni$75°F$ hivyo$T_s=75$. Joto la pizza linapotoka nje ya tanuri ni$350°F$, ambayo ni joto la awali (yaani, thamani ya awali), hivyo$T_0=350$. Kwa hiyo Equation\ ref {Newton} inakuwa

$$\dfrac{dT}{dt}=k(T−75) \nonumber$$

na$T(0)=350.$

Ili kutatua equation tofauti, tunatumia mbinu ya hatua tano ya kutatua equations inayoweza kutenganishwa.

1. Kuweka upande wa kulia sawa na sifuri hutoa$T=75$ kama suluhisho la mara kwa mara. Tangu pizza huanza saa$350°F,$ hii sio suluhisho tunayotafuta.

2. Andika upya equation tofauti kwa kuzidisha pande zote mbili$dt$ na kugawanya pande zote mbili kwa$T−75$:

$$\dfrac{dT}{T−75}=k\,dt. \nonumber$$

3. Unganisha pande zote mbili:

$$\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber$$

4. Tatua$T$ kwa kwanza kutafakari pande zote mbili:

$$\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber$$

5. Tatua$C$ kwa kutumia hali ya awali$T(0)=350:$

$$\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber$$

Kwa hiyo, suluhisho la tatizo la thamani ya awali ni

$$T(t)=75+275e^{kt}.\nonumber$$

Kuamua thamani ya$k$, tunahitaji kutumia ukweli kwamba baada ya$5$ dakika joto la pizza ni$340°F$. Kwa hiyo$T(5)=340.$ Kubadilisha habari hii katika suluhisho la tatizo la thamani ya awali, tuna

$$T(t)=75+275e^{kt}\nonumber$$

$$T(5)=340=75+275e^{5k}\nonumber$$

$$265=275e^{5k}\nonumber$$

$$e^{5k}=\dfrac{53}{55}\nonumber$$

$$\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber$$

$$5k=\ln(\dfrac{53}{55})\nonumber$$

$$k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber$$

Hivyo sasa tuna$T(t)=75+275e^{−0.007048t}.$ wakati gani joto$300°F$? Kutatua kwa$t,$ tunapata

$$T(t)=75+275e^{−0.007048t}\nonumber$$

$$300=75+275e^{−0.007048t}\nonumber$$

$$225=275e^{−0.007048t}\nonumber$$

$$e^{−0.007048t}=\dfrac{9}{11}\nonumber$$

$$\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber$$

$$−0.007048t=\ln\dfrac{9}{11}\nonumber$$

$$t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber$$

Kwa hiyo tunahitaji kusubiri$23.5$ dakika ya ziada (baada ya joto la pizza kufikiwa$340°F$). Hiyo inapaswa kuwa muda wa kutosha tu kumaliza hesabu hii.

Zoezi$\PageIndex{4}$

Keki huondolewa kwenye tanuri baada ya kuoka vizuri, na joto la tanuri ni$450°F$. Joto la jikoni ni$70°F$, na baada ya$10$ dakika joto la keki ni$430°F$.

1. Andika tatizo sahihi la thamani ya awali ili kuelezea hali hii.
2. Tatua tatizo la thamani ya awali kwa$T(t)$.
3. Itachukua muda gani mpaka joto la keki liko ndani$5°F$ ya joto la kawaida?

Kidokezo

Kuamua maadili ya$T_s$ na$T_0$ kisha kutumia Equation\ ref {Newton}.

Jibu

Tatizo la thamani ya awali $$\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber$$

Jibu b

$$T(t)=70+380e^{kt}\nonumber$$

Jibu c

Takriban$114$ dakika.

Dhana muhimu

• Equation tofauti tofauti ni equation yoyote ambayo inaweza kuandikwa kwa fomu$y'=f(x)g(y).$
• Njia ya kujitenga kwa vigezo hutumiwa kupata suluhisho la jumla kwa equation tofauti tofauti.

Mlinganyo muhimu

• Kutenganishwa tofauti equation

$y′=f(x)g(y)$

• Solution mkusanyiko

$\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}$

• Sheria ya Newton ya baridi

$\dfrac{dT}{dt}=k(T−T_s)$

faharasa

uhuru tofauti equation

equation ambayo upande wa kulia ni kazi ya$y$ peke yake

tofauti tofauti equation

equation yoyote ambayo inaweza kuandikwa kwa fomu$y'=f(x)g(y)$

kujitenga kwa vigezo

njia inayotumiwa kutatua equation tofauti tofauti