8.2: Mashamba ya Mwelekeo na Njia za Nambari

Last updated
Save as PDF

Page ID: 178772

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Chora uwanja mwelekeo kwa kupewa kwanza ili tofauti equation.
Tumia uwanja wa mwelekeo kuteka safu ya suluhisho ya equation ya kwanza ya tofauti.
Tumia Method ya Euler ili takriban suluhisho la equation ya kwanza ya tofauti.

Kwa sura hii yote tutazingatia mbinu mbalimbali za kutatua equations tofauti na kuchambua tabia ya ufumbuzi. Katika baadhi ya matukio inawezekana kutabiri mali ya suluhisho la equation tofauti bila kujua suluhisho halisi. Tutajifunza pia mbinu za namba za kutatua equations tofauti, ambazo zinaweza kupangwa kwa kutumia lugha mbalimbali za kompyuta au hata kwa kutumia programu ya sahajedwali, kama vile Microsoft Excel.

Kujenga Mashamba ya Mwelekeo

Mashamba ya mwelekeo (pia huitwa mashamba ya mteremko) ni muhimu kwa kuchunguza usawa wa kwanza wa tofauti. Hasa, tunazingatia equation ya kwanza ya tofauti ya fomu

\[ y'=f(x,y).\nonumber \]

Mfano uliotumika wa aina hii ya usawa tofauti unaonekana katika sheria ya Newton ya baridi, ambayo tutatatua wazi baadaye katika sura hii. Kwanza, ingawa, hebu kujenga uwanja mwelekeo kwa equation tofauti

\[ T′(t)=−0.4(T−72).\nonumber \]

Hapa$ T(t)$ inawakilisha joto (katika digrii Fahrenheit) ya kitu kwa wakati$ t$, na joto iliyoko ni$ 72°F$. Kielelezo$ \PageIndex{1}$ inaonyesha uwanja mwelekeo kwa equation hii.

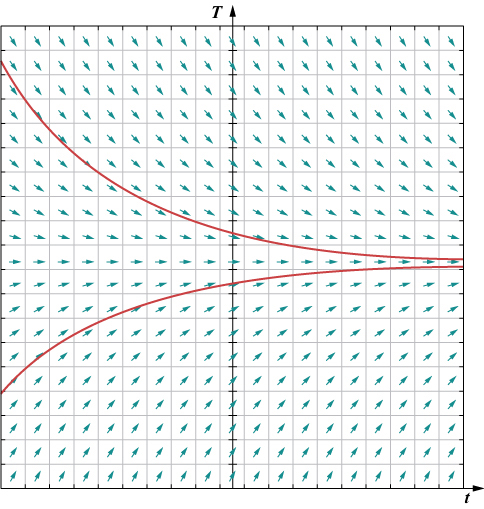
Grafu ya uwanja wa mwelekeo kwa equation tofauti iliyotolewa katika quadrants moja na mbili. Mishale inaelezea moja kwa moja na haki katika y = 72. Chini ya mstari huo, mishale imezidi mteremko mzuri kama y inakuwa ndogo. Juu ya mstari huo, mishale imezidi mteremko hasi kama y inakuwa kubwa. Mishale inaelezea kuunganishwa kwa y = 72. Ufumbuzi mbili hutolewa: moja kwa joto la awali chini ya 72, na moja kwa joto la awali kubwa kuliko 72. Suluhisho la juu ni kupungua kwa concave up Curve, inakaribia y = 72 kama t inakwenda infinity. Suluhisho la chini ni kuongezeka kwa concave chini, inakaribia y = 72 kama t inakwenda infinity. — Kielelezo$ \PageIndex{1}$: Mwelekeo shamba kwa equation tofauti$ T′(t)=−0.4(T−72)$. Ufumbuzi mbili ni njama: moja na joto la awali chini$ 72°F$ na nyingine na joto la awali kubwa kuliko$ 72°F$.

Wazo nyuma ya uwanja wa mwelekeo ni ukweli kwamba derivative ya kazi tathmini katika hatua fulani ni mteremko wa mstari tangent kwa grafu ya kazi hiyo kwa hatua moja. Mifano mingine ya equations tofauti ambayo tunaweza kuunda uwanja wa mwelekeo ni pamoja na

\[ y'=3x+2y−4\nonumber \]

\[ y'=x^2−y^2\nonumber \]

\[ y'=\frac{2x+4}{y−2}.\nonumber \]

Ili kujenga uwanja wa mwelekeo, tunaanza na equation ya kwanza:$ y'=3x+2y−4$. Sisi basi$ \left(x_0,\, y_0\right)$ kuwa jozi yoyote awali, na sisi badala namba hizi katika upande wa kulia wa equation tofauti. Kwa mfano, kama sisi kuchagua$ x=1$ na$ y=2$, badala katika upande wa kulia wa tofauti equation mavuno

$ y′=3x+2y−4=3(1)+2(2)−4=3.$

Hii inatuambia kwamba ikiwa suluhisho la equation tofauti$ y'=3x+2y−4$ hupita kupitia hatua$ (1,2)$, basi mteremko wa suluhisho katika hatua hiyo lazima iwe sawa 3. Ili kuanza kujenga uwanja wa mwelekeo, tunaweka sehemu ya mstari mfupi kwenye hatua$ (1,2)$ iliyo na mteremko$ 3$. Tunaweza kufanya hivyo kwa hatua yoyote katika uwanja wa kazi$ f(x,y)=3x+2y−4,$ ambayo ina jozi zote kuamuru$ (x,y)$ katika$ R^2$. Kwa hiyo hatua yoyote katika ndege ya Cartesian ina mteremko unaohusishwa nayo, kudhani kuwa suluhisho la equation tofauti hupita kupitia hatua hiyo. Sehemu ya mwelekeo kwa equation tofauti$ y′=3x+2y−4$ inavyoonekana kwenye Kielelezo$ \PageIndex{2}$.

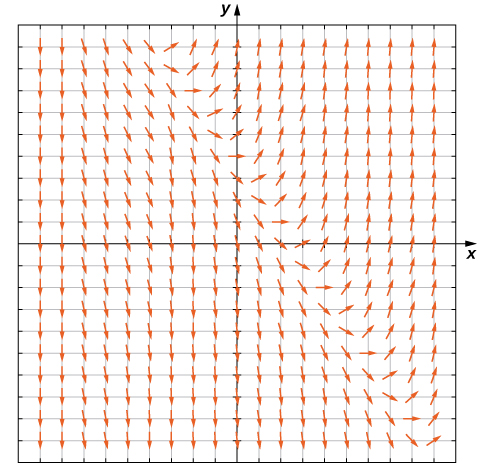
Grafu ya uwanja wa mwelekeo kwa equation tofauti y' = 3 x + 2 y - 4 katika quadrants zote nne. Katika quadrants mbili na tatu, mishale inaelezea chini na kidogo kwa haki. Kwenye mstari wa diagonal, takribani y = -x + 2, mishale inaelezea zaidi na zaidi kwa haki, safu, na kisha uelekeze juu ya mstari huo. — Kielelezo$ \PageIndex{2}$: Mwelekeo shamba kwa equation tofauti$ y'=3x+2y−4$.

Tunaweza kuzalisha uwanja wa mwelekeo wa aina hii kwa equation yoyote tofauti ya fomu$ y'=f(x,y).$

Ufafanuzi: Uwanja wa Mwelekeo (Uwanja wa S

Shamba la mwelekeo (uwanja wa mteremko) ni kitu cha hisabati kinachotumiwa kuwakilisha graphically ufumbuzi wa equation tofauti ya kwanza. Katika kila hatua katika uwanja wa mwelekeo, sehemu ya mstari inaonekana ambayo mteremko wake ni sawa na mteremko wa suluhisho la equation tofauti inayopita kupitia hatua hiyo.

Kutumia Maeneo ya Mwelekeo

Tunaweza kutumia uwanja wa mwelekeo kutabiri tabia ya ufumbuzi wa equation tofauti bila kujua ufumbuzi halisi. Kwa mfano, uwanja wa mwelekeo katika Kielelezo$ \PageIndex{3}$ hutumika kama mwongozo wa tabia ya ufumbuzi wa equation tofauti$ y'=3x+2y−4.$

Ili kutumia uwanja wa mwelekeo, tunaanza kwa kuchagua hatua yoyote kwenye shamba. Sehemu ya mstari katika hatua hiyo hutumika kama ishara ya kutuambia ni mwelekeo gani wa kwenda kutoka huko. Kwa mfano, ikiwa suluhisho la equation tofauti hupita kupitia hatua$ (0,1),$ basi mteremko wa suluhisho unaopitia hatua hiyo hutolewa na$ y'=3(0)+2(1)−4=−2.$ Sasa basi$ x$ ongezeko kidogo, sema$ x=0.1$. Kwa kutumia njia ya makadirio linear anatoa formula kwa thamani takriban ya$ y$ kwa$ x=0.1.$ Hasa,

\[ L(x)=y_0+f′(x_0)(x−x_0)=1−2(x_0−0)=1−2x_0.\nonumber \]

Kubadilisha$ x_0=0.1$ katika$ L(x)$ anatoa$ y$ thamani takriban ya$ 0.8$.

Kwa hatua hii mteremko wa suluhisho hubadilika (tena kulingana na equation tofauti). Tunaweza kuendelea, kurejesha mteremko wa suluhisho tunapochukua hatua ndogo kwa haki, na kuangalia tabia ya suluhisho. Kielelezo$ \PageIndex{3}$ kinaonyesha grafu ya suluhisho inayopitia hatua$ (0,1)$.

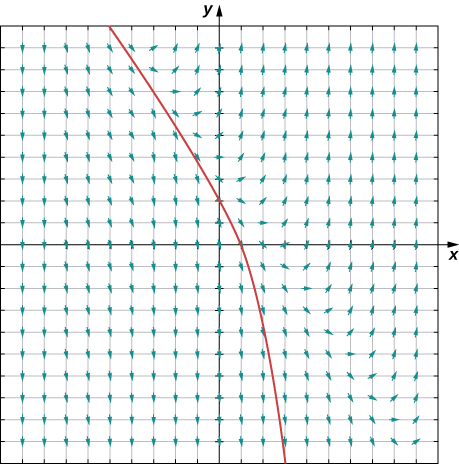
Curve ni grafu ya suluhisho la tatizo la thamani ya awali

\[ y'=3x+2y−4,\; y(0)=1.\nonumber \]

Curve hii inaitwa ufumbuzi Curve kupita kwa njia$ (0,1).$ ya uhakika. ufumbuzi halisi ya tatizo hili awali thamani ni

\[ y=−\frac{3}{2}x+\frac{5}{4}−\frac{1}{4}e^{2x},\nonumber \]

na grafu ya ufumbuzi huu ni sawa na Curve katika Kielelezo$ \PageIndex{3}$.

Zoezi$\PageIndex{1}$

Kujenga uwanja mwelekeo kwa equation tofauti$ y'=x^2−y^2$ na mchoro ufumbuzi Curve kupitia hatua$ (−1,2)$.

Kidokezo: Matumizi$ x$ na$ y$ maadili kuanzia$ −5$ hadi$ 5$. Kwa kila jozi ya kuratibu, hesabu kwa$ y'$ kutumia upande wa kulia wa equation tofauti.

Jibu: $Grafu ya uwanja wa mwelekeo kwa equation tofauti y' = x ^ 2 - y ^ 2. Pamoja y = x na y = -x, mistari ni ya usawa. Kwa upande wowote wa y = x na y = -x, mistari ya slant na ufumbuzi wa moja kwa moja pamoja na kazi hizo mbili. Wengine wa mistari ni wima. Suluhisho linalopitia (-1, 2) linaonyeshwa. Ni curves chini kutoka juu (-2.75, 10), kupitia (-1, 2) na kuhusu (0, 1.5), na kisha juu ya diagonal kwa (10, 10).$

Sasa fikiria uwanja wa mwelekeo kwa usawa tofauti$ y'=(x−3)(y^2−4)$, umeonyeshwa kwenye Kielelezo$ \PageIndex{4}$. Shamba hili la mwelekeo lina mali kadhaa za kuvutia. Awali ya yote, saa$ y=−2$ na$ y=2$, dashes za usawa zinaonekana njia yote kwenye grafu. Hii ina maana kwamba kama$ y=−2$, kisha$ y'=0.$ Kubadilisha maneno haya katika upande wa kulia wa equation tofauti anatoa

\ [kuanza {align*} (x-3) (y ^ 2,14) &= (x-3) (-2) ^2,14)\\ [4pt]
& =( x-3) (0)\\ [4pt]
&=0\\ [4pt]
&=y'. \ mwisho {align*}\]

Kwa hiyo$ y=−2$ ni suluhisho la equation tofauti. Vile vile,$ y=2$ ni suluhisho la equation tofauti. Hizi ni tu mara kwa mara thamani ufumbuzi wa equation tofauti, kama tunaweza kuona kutoka hoja zifuatazo. Tuseme$ y=k$ ni suluhisho la mara kwa mara kwa usawa tofauti. Kisha$ y′=0$. Kubadilisha maneno haya katika mavuno tofauti ya equation$ 0=(x−3)(k^2−4)$. Equation Hii lazima kweli kwa maadili yote ya$ x$, hivyo sababu ya pili lazima sawa sifuri. Matokeo haya huzaa equation$ k^2−4=0$. Ufumbuzi wa equation hii ni$ k=−2$ na$ k=2$, ambayo ni ufumbuzi wa mara kwa mara uliotajwa tayari. Hizi huitwa ufumbuzi wa usawa kwa equation tofauti.

uwanja mwelekeo kwa ajili ya kutolewa tofauti equation. Mishale ni ya usawa na inaelezea haki katika y = -2, y = 2, na x = 3. Mishale ya karibu ni x = 6, mishale ya usawa zaidi inakuwa. Mbali zaidi, wima zaidi ni. — Kielelezo$ \PageIndex{4}$: Mwelekeo shamba kwa equation tofauti$ y'=(x−3)(y^2−4)$ kuonyesha ufumbuzi mbili. Ufumbuzi huu ni karibu sana pamoja, lakini moja ni vigumu juu ya ufumbuzi wa usawa$ x=−2$ na nyingine ni vigumu chini ya ufumbuzi huo wa usawa.

Ufafanuzi: E usawa Solutions

Fikiria equation tofauti$ y'=f(x,y)$. Suluhisho la usawa ni suluhisho lolote la usawa tofauti wa fomu$ y=c$, ambapo$c$ ni mara kwa mara.

Kuamua ufumbuzi wa usawa kwa usawa tofauti$ y'=f(x,y)$, weka upande wa kulia sawa na sifuri. ufumbuzi msawazo wa equation tofauti ni kazi yoyote ya fomu$ y=k$ kama kwamba$ f(x,k)=0$ kwa maadili yote ya$ x$ katika uwanja wa$ f$.

tabia muhimu ya ufumbuzi msawazo wasiwasi kama au wao mbinu line$ y=k$ kama asymptote kwa maadili kubwa ya$ x$.

Ufafanuzi: Ufumbuzi usio imara, usio na uhakika na Semi-Imara

Fikiria equation tofauti$ y′=f(x,y),$ na kudhani kwamba ufumbuzi wote wa equation hii tofauti hufafanuliwa kwa$ x≥x_0$. Hebu$ y=k$ kuwa suluhisho la usawa kwa equation tofauti.

$ y=k$ni ufumbuzi asymptotically imara kwa equation tofauti kama kuna$ ε>0$ vile kwamba kwa thamani yoyote ufumbuzi$ c∈(k−ε,\, k+ε)$ wa tatizo awali thamani$ y′=f(x,y), \; y(x_0)=c$ inakaribia$ k$ kama$ x$ mbinu infinity.
$ y=k$ni ufumbuzi asymptotically msimamo kwa equation tofauti kama kuna$ ε>0$ vile kwamba kwa thamani yoyote ufumbuzi$ c∈(k−ε,\, k+ε)$ wa tatizo awali thamani$ y′=f(x,y), \; y(x_0)=c$ kamwe mbinu$ k$ kama$ x$ mbinu infinity.
$ y=k$ni suluhisho isiyo ya kawaida ya nusu imara kwa equation tofauti ikiwa sio imara imara au isiyo imara.

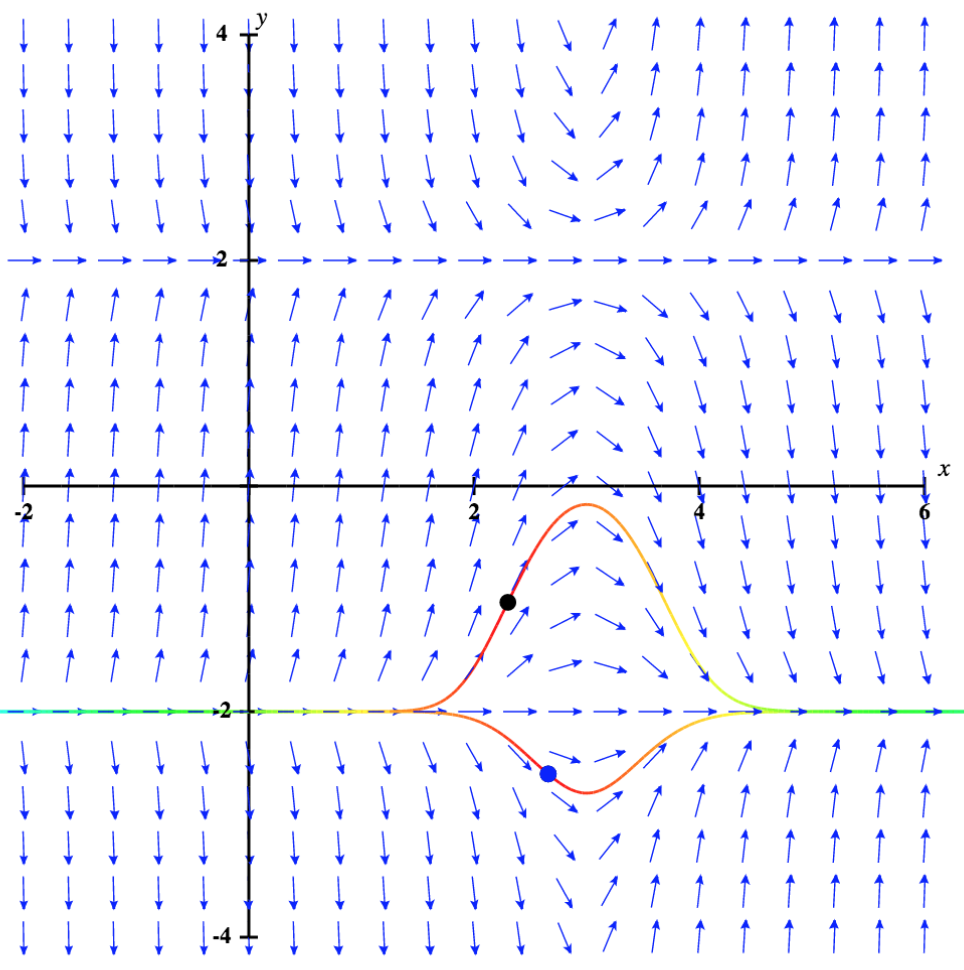
Sasa tunarudi kwenye usawa tofauti$ y'=(x−3)(y^2−4)$, na hali ya awali$ y(0)=0.5$. Sehemu ya mwelekeo kwa tatizo hili la thamani ya awali, pamoja na suluhisho linalofanana, linaonyeshwa kwenye Kielelezo$ \PageIndex{5}$.

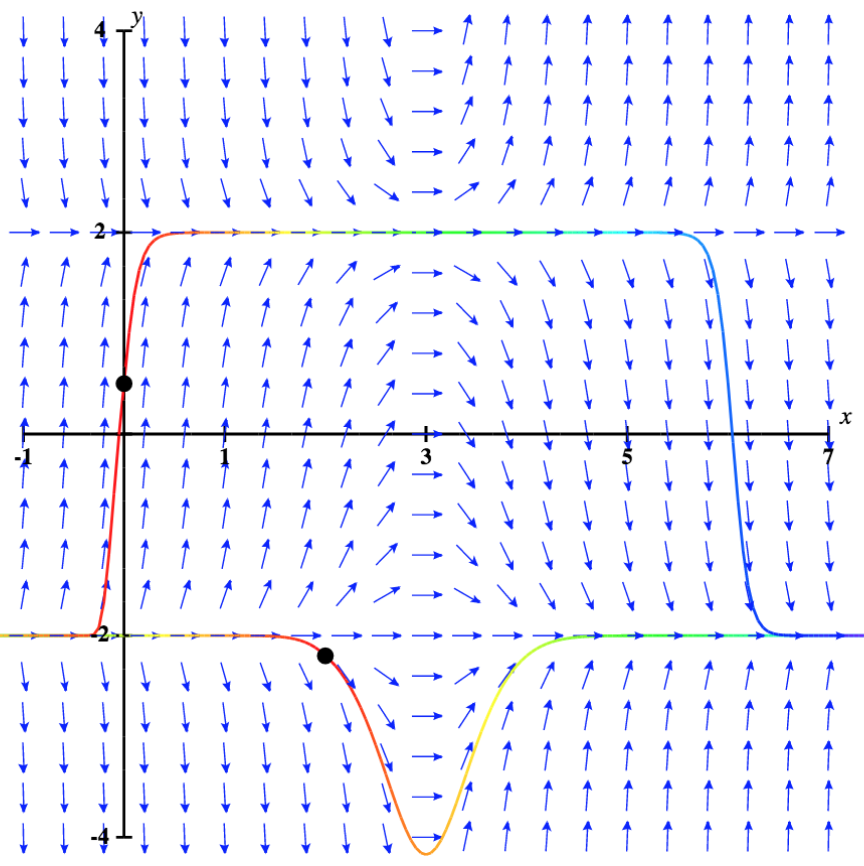
uwanja mwelekeo kwa ajili ya kutolewa tofauti equation. Mishale ni ya usawa na inaelezea haki katika y = -2, y = 2, na x = 3. Suluhisho linapatikana kwa njia ya (0, 0.5) na mwingine kupitia hatua (2, -2.2). Wote curves hatimaye mbinu line y = -2 asymptotically.. — Kielelezo$ \PageIndex{5}$: Shamba la mwelekeo kwa tatizo la thamani$ y'=(x−3)(y^2−4),\; y(0)=0.5.$ ya awali Curve ya pili ya suluhisho imewekwa na hali ya awali$(2, -2.2)$.

Maadili ya suluhisho la tatizo hili la thamani ya awali hukaa kati$ y=−2$ na$ y=2$, ambayo ni ufumbuzi wa usawa wa equation tofauti. Zaidi ya hayo, kama$ x$ mbinu infinity, ingawa awali kuonekana mbinu line y = 2,$ y$ -kuratibu wazi mbinu$ -2$. Tabia ya ufumbuzi ni sawa kama thamani ya awali iko chini$ -2$, kwa mfano,$ y(2)=-2.2$. Katika kesi hiyo, ufumbuzi huongezeka na mbinu$ y=-2$ kama$ x$ inakaribia infinity. Kwa hiyo$ y=-2$ ni suluhisho asymptotically imara kwa equation hii tofauti.

Ni nini kinachotokea wakati thamani ya awali iko juu$ y=2$? Hali hii ni mfano katika Kielelezo$ \PageIndex{6}$, na thamani ya awali$ y(0)=3.$

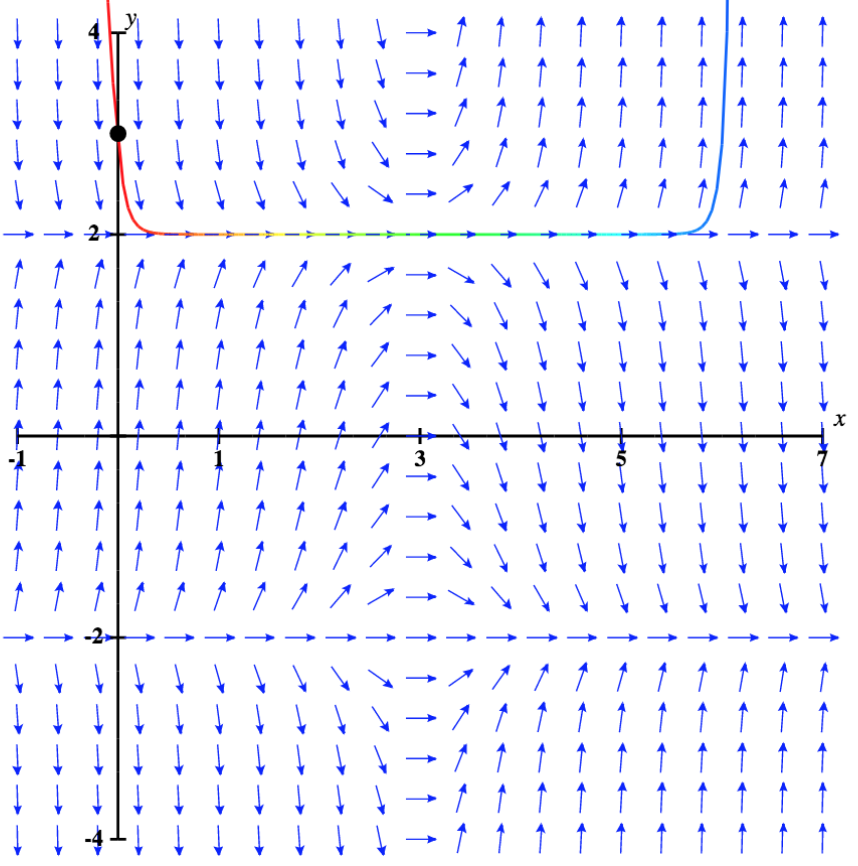
uwanja mwelekeo kwa ajili ya kupewa tofauti equation. Mishale ni ya usawa na inaelezea haki katika y = -2, y = 2, na x = 3. ufumbuzi ni graphed kwamba huenda pamoja y = 2 katika roboduara 1 kati x = 0 na x = 6 na kisha huenda infinity chanya, kama x inaendelea kuelekea infinity. — Kielelezo$ \PageIndex{6}$: Shamba la mwelekeo kwa tatizo la thamani ya awali$ y'=(x−3)(y^2−4),\; y(0)=3.$

Suluhisho huongezeka kwa kasi kuelekea infinity chanya kama$ x$ mbinu infinity. Zaidi ya hayo, ikiwa thamani ya awali ni kidogo chini$ 2$, basi ufumbuzi unakaribia$ -2$, ambayo ni ufumbuzi mwingine wa usawa. Kwa hiyo katika hali yoyote hakuna njia ya suluhisho$ y=2$, hivyo$ y=2$ inaitwa ufumbuzi usio na uhakika, au usio na uhakika, ufumbuzi wa usawa.

Mfano$ \PageIndex{1}$: Stability of an Equilibrium Solution

Unda uwanja wa mwelekeo kwa equation tofauti$ y'=(y−3)^2(y^2+y−2)$ na kutambua ufumbuzi wowote wa usawa. Kuainisha kila ufumbuzi wa usawa kama imara, imara, au nusu imara.

Suluhisho

Shamba la mwelekeo linaonyeshwa kwenye Kielelezo$ \PageIndex{7}$.

Grafu ya uwanja wa mwelekeo na mishale inayoelezea haki katika y = -4, y = 2, na y = 6. Kwa y <-4, mishale inaelekeza. Kwa -4 <y <2, mishale inaelekeza chini. Kwa 2 <y <6, mishale inaelekeza juu, ikawa ya kupendeza na ya kupendeza wanapokaribia y = 6. Kwa y — Kielelezo$ \PageIndex{7}$: Shamba la mwelekeo kwa equation tofauti$ y'=(y−3)^2(y^2+y−2).$

Ufumbuzi wa usawa ni$ y=−2,\, y=1,$ na$ y=3$. Ili kuainisha kila ufumbuzi, angalia mshale moja kwa moja juu au chini ya kila moja ya maadili haya. Kwa mfano,$ y=−2$ kwenye mishale moja kwa moja chini ya ufumbuzi huu unasimama, na mishale moja kwa moja juu ya ufumbuzi huelekea chini. Kwa hiyo hali zote za awali karibu na$ y=−2$ mbinu$ y=−2$, na suluhisho ni imara. Kwa ajili ya suluhisho$ y=1$, hali zote za awali hapo juu na chini$ y=1$ zinakabiliwa (kusukwa mbali) kutoka$ y=1$, hivyo suluhisho hili haliwezi kushikamana. Suluhisho$ y=3$ ni nusu imara, kwa sababu kwa hali ya awali kidogo zaidi kuliko$ 3$, suluhisho linakaribia infinity, na kwa hali ya awali kidogo chini ya$ 3$, ufumbuzi unakaribia$ y=1$.

Uchambuzi

Inawezekana kupata ufumbuzi wa usawa kwa equation tofauti kwa kuweka upande wa kulia sawa na sifuri na kutatua kwa Njia$ y.$ hii inatoa ufumbuzi sawa wa usawa kama yale tuliyoyaona katika uwanja wa mwelekeo.

Zoezi$\PageIndex{2}$

Unda uwanja wa mwelekeo kwa equation tofauti$ y'=(x+5)(y+2)(y^2−4y+4)$ na kutambua ufumbuzi wowote wa usawa. Kuainisha kila ufumbuzi wa usawa kama imara, imara, au nusu imara.

Kidokezo: Kwanza uunda uwanja wa mwelekeo na uangalie dashes za usawa zinazoenda njia yote. Kisha kuchunguza mistari ya mteremko moja kwa moja juu na chini ya ufumbuzi wa usawa.

Jibu

Ufumbuzi wa usawa ni$ y=−2$ na$ y=2$. Kwa equation hii,$ y=−2$ ni msimamo msawazo ufumbuzi, na$ y=2$ ni nusu imara msawazo ufumbuzi.

Shamba la mwelekeo na mishale inayoelezea haki katika y = -4 na y = 4. Mishale inaelekeza kwa y -4 na chini kwa y <-4. Karibu na y = 4, mishale ni ya usawa zaidi, lakini mbali zaidi, wima zaidi huwa." src="https://math.libretexts.org/@api/dek...2452/8.2.3.png">

Njia ya Euler

Fikiria tatizo la thamani ya awali

\[ y′=2x−3,\;y(0)=3.\nonumber \]

Kuunganisha pande zote mbili za equation tofauti anatoa$ y=x^2−3x+C,$ na kutatua kwa$ C$ mavuno ufumbuzi$ y=x^2−3x+3.$ hasa. ufumbuzi kwa tatizo hili awali thamani inaonekana kama parabola katika Kielelezo$ \PageIndex{8}$.

Grafu juu ya aina mbalimbali [-1,4] kwa x na y. kupewa zaidi ufunguzi parabola ni inayotolewa na kipeo katika (1.5, 0.75). Pointi za kibinafsi zimepangwa (0, 3), (0.5, 1.5), (1, 0.5), (1.5, 0), (2, 0), (2.5, 0.5), na (3, 1.5) na makundi ya mstari yanayounganisha. — Kielelezo$ \PageIndex{8}$: Njia ya Euler kwa tatizo la thamani ya awali$ y′=2x−3,y(0)=3.$

Grafu nyekundu ina makundi ya mstari ambayo yanakaribia suluhisho la tatizo la thamani ya awali. Grafu huanza kwa thamani sawa ya awali ya$ (0,3)$. Kisha mteremko wa suluhisho wakati wowote unatambuliwa na upande wa kulia wa equation tofauti, na urefu wa sehemu ya mstari imedhamiriwa na kuongeza$ x$ thamani kwa$ 0.5$ kila wakati (ukubwa wa hatua). Njia hii ni msingi wa Method ya Euler.

Kabla ya kusema Njia ya Euler kama theorem, hebu tuchunguze tatizo lingine la thamani ya awali:

\[ y′=x^2−y^2,\; y(−1)=2.\nonumber \]

Wazo nyuma ya mashamba ya uongozi pia inaweza kutumika kwa tatizo hili kujifunza tabia ya suluhisho lake. Kwa mfano, wakati huo$ (−1,2),$ mteremko wa suluhisho hutolewa na$ y'=(−1)^2−2^2=−3$, hivyo mteremko wa mstari wa tangent kwa suluhisho wakati huo pia ni sawa na$ −3$. Sasa tunafafanua$ x_0=−1$ na$ y_0=2$. Kwa kuwa mteremko wa suluhisho katika hatua hii ni sawa na$ −3$, tunaweza kutumia njia ya makadirio ya mstari kwa takriban y karibu$ (−1,2)$.

\[ L(x)=y_0+f′(x_0)(x−x_0).\nonumber \]

Hapa$ x_0=−1,y_0=2,$ na$ f′(x_0)=−3,$ hivyo makadirio linear inakuwa

\[ L(x)=2−3(x−(−1))=2−3x−3=−3x−1.\nonumber \]

Sasa tunachagua ukubwa wa hatua. Ukubwa wa hatua ni thamani ndogo, kwa kawaida$ 0.1$ au chini, ambayo hutumika kama nyongeza ya$ x$; inawakilishwa na kutofautiana$ h$. Katika mfano wetu, basi$ h=0.1$. Kuongeza$ x_0$ kwa$ h$ anatoa$ x$ thamani yetu ijayo:

\[ x_1=x_0+h=−1+0.1=−0.9.\nonumber \]

Tunaweza mbadala$ x_1=−0.9$ katika makadirio linear kwa mahesabu$ y_1$.

\[ y_1=L(x_1)=−3(−0.9)−1=1.7.\nonumber \]

Kwa hiyo$ y$ thamani ya takriban ya suluhisho wakati$ x=−0.9$ ni$ y=1.7$. Tunaweza kurudia mchakato, kutumia$ x_1=−0.9$ na$ y_1=1.7$ kuhesabu$ x_2$ na$ y_2$. mteremko mpya ni iliyotolewa na$ y'=(−0.9)^2−(1.7)^2=−2.08.$ Kwanza, Kwa$ x_2=x_1+h=−0.9+0.1=−0.8.$ kutumia linear makadirio anatoa

\ (kuanza {align*} L (x) &=y_1+f (x_1) (x-x_1)\\ [4pt]
&=1.7,12.08 (x-0.9))\\ [4pt]
&=1.7,18x-1.872\\ [4pt]
&=-2.08x-0.172. \ mwisho {align*}\)

Hatimaye, sisi badala$ x_2=−0.8$ katika makadirio linear kwa mahesabu$ y_2$.

\ (\ kuanza {align*} Y_2&=L (x_2)\\ [4pt]
&=—2.08x_2,12,12\\ [4pt]
&=-2.08 (-0.8) -0.172\\ [4pt]
&=1.492. \ mwisho {align*}\)

Kwa hiyo, thamani ya takriban ya suluhisho la usawa tofauti ni$ y=1.492$ wakati$ x=−0.8.$

Nini sisi tu umeonyesha ni wazo nyuma Method Euler ya. Kurudia hatua hizi hutoa orodha ya maadili kwa suluhisho. Maadili haya yanaonyeshwa kwenye meza, yamezunguka hadi sehemu nne za decimal.

Jedwali$ \PageIndex{1}$: Kutumia Njia ya Euler kwa Ufumbuzi wa Takriban kwa Equation Tofauti
$ n$	0	1	2	3	4	5
$ x_n$	-1	-0.9	-0.8	-0.7	-0.6	-0.5
$ y_n$	2	1.7	1.492	1.3334	1.2046	1.0955
$ n$	6	7	8	9	10
$ x_n$	-0.4	-0.3	-0.2	-0.1	0
$ y_n$	1.0004	1.9164	1.8414	1.7746	1.7156

Njia ya Euler

Fikiria tatizo la thamani ya awali

\[ y'=f(x,y),\; y(x_0)=y_0.\nonumber \]

Ili takriban suluhisho la tatizo hili kwa kutumia njia ya Euler, fafanua

$ x_n=x_0+nh$

$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$.

Hapa$ h>0$ inawakilisha ukubwa wa hatua na$ n$ ni integer, kuanzia na$ 1$. Idadi ya hatua zilizochukuliwa zinahesabiwa na kutofautiana$ n$.

Kwa kawaida$ h$ ni thamani ndogo, sema$ 0.1$ au$ 0.05$. Thamani ndogo ya$ h$, mahesabu zaidi yanahitajika. Ya juu ya thamani ya$ h$, mahesabu machache yanahitajika. Hata hivyo, matokeo ya biashara katika kiwango cha chini cha usahihi kwa ukubwa kubwa hatua, kama inavyoonekana katika Kielelezo$ \PageIndex{9}$.

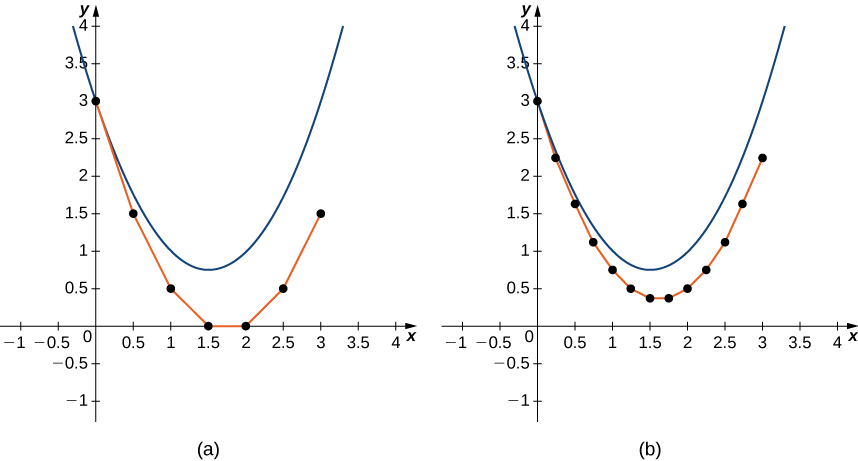
Grafu mbili za parabola sawa, y = x ^ 2 - 3 x + 3. Ya kwanza inaonyesha njia ya Euler kwa tatizo la thamani ya awali na ukubwa wa hatua ya h = 0.05, na pili inaonyesha njia ya Euler na ukubwa wa hatua ya h = 0.25. Ya kwanza basi ina pointi (0, 3), (.5, 1.5), (1, 0.5), (1.5, 0), (2, 0), (2.5, 0.5), na (3, 1.5) zilizopangwa na makundi ya mstari kuunganisha. Ya pili ina pointi (0, 3), (0.25, 2.25), (0.5, 1.625), (0.75, 1.125), (1, 0.75), (1.25, 0.5), (1.5, 0.375), (2, 0.5), (2.25, 0.75), (2.5, 1.125), (2.75, 1.625), na (3, 2.25) plot ttted na makundi line kuunganisha yao. — Kielelezo$ \PageIndex{9}$: Mbinu Euler kwa tatizo awali thamani$ y′=2x−3,\; y(0)=3$ na (a) hatua ukubwa wa$ h=0.5$; na (b) hatua ukubwa wa$ h=0.25.$

Mfano$ \PageIndex{2}$: Using Euler’s Method

Fikiria tatizo la thamani ya awali

\[ y′=3x^2−y^2+1,\; y(0)=2.\nonumber \]

Kutumia njia Euler na hatua ukubwa wa$ 0.1$ kuzalisha meza ya maadili kwa ufumbuzi kwa ajili ya maadili ya$ x$ kati$ 0$ na$ 1$.

Suluhisho

Tunapewa$ h=0.1$ na$ f(x,y)=3x^2−y^2+1.$ Zaidi ya hayo, hali ya awali$ y(0)=2$ inatoa$ x_0=0$ na$ y_0=2$. Kutumia Equation na$ n=0$, tunaweza kuzalisha meza hii.

Jedwali$ \PageIndex{2}$: Kutumia Njia ya Euler kwa Ufumbuzi wa Takriban kwa Equation Tofauti
$ n$	$ x_n$	$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$
\ (n\)” style="wima align:katikati; "> 0	\ (x_n\)” style="wima align:katikati; "> 0	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; "> 2
\ (n\)” style="wima align:katikati; "> 1	\ (x_n\)” style="wima align:katikati; "> 0.1	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_1=y_0+hf(x_0,y_0)=1.7$
\ (n\)” style="wima align:katikati; "> 2	\ (x_n\)” style="wima align:katikati; "> 0.2	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_2=y_1+hf(x_1,y_1)=1.514$
\ (n\)” style="wima align:katikati; "> 3	\ (x_n\)” style="wima align:katikati; "> 0.3	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_3=y_2+hf(x_2,y_2)=1.3968$
\ (n\)” style="wima align:katikati; "> 4	\ (x_n\)” style="wima align:katikati; "> 0.4	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_4=y_3+hf(x_3,y_3)=1.3287$
\ (n\)” style="wima align:katikati; "> 5	\ (x_n\)” style="wima align:katikati; "> 0.5	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_5=y_4+hf(x_4,y_4)=1.3001$
\ (n\)” style="wima align:katikati; "> 6	\ (x_n\)” style="wima align:katikati; "> 0.6	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_6=y_5+hf(x_5,y_5)=1.3061$
\ (n\)” style="wima align:katikati; "> 7	\ (x_n\)” style="wima align:katikati; "> 0.7	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_7=y_6+hf(x_6,y_6)=1.3435$
\ (n\)” style="wima align:katikati; "> 8	\ (x_n\)” style="wima align:katikati; "> 0.8	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_8=y_7+hf(x_7,y_7)=1.4100$
\ (n\)” style="wima align:katikati; "> 9	\ (x_n\)” style="wima align:katikati; "> 0.9	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_9=y_8+hf(x_8,y_8)=1.5032$
\ (n\)” style="wima align:katikati; "> 10	\ (x_n\)” style="wima align:katikati; "> 1.0	\ (y_n=y_ {n-1} +hf (x_ {n-1}, y_ {n-1})\)” style="wima align:katikati; ">$ y_{10}=y_9+hf(x_9,y_9)=1.6202$

Kwa mahesabu kumi, tuna uwezo wa kulinganisha maadili ya suluhisho kwa tatizo la thamani ya awali kwa maadili ya$ x$ kati$ 0$ na$ 1$.

Nenda kwenye tovuti hii kwa nafasi ya kuibua kuchunguza njia ya Euler.

Zoezi$\PageIndex{3}$

Fikiria tatizo la thamani ya awali

\[ y′=x^3+y^2,\; y(1)=−2.\nonumber \]

Kwa kutumia hatua ukubwa wa$ 0.1$, kuzalisha meza na maadili takriban kwa ufumbuzi wa tatizo awali thamani kwa maadili ya$ x$ kati$ 1$ na$ 2$.

Kidokezo: Anza kwa kutambua thamani ya$ h$, kisha kufikiri nini$ f(x,y)$ ni. Kisha utumie fomu ya Njia ya Euler ili kuhesabu$ y_1,y_2,$ na kadhalika.

Jibu

Jedwali$ \PageIndex{3}$: Kutumia Method Euler kwa takriban ufumbuzi wa equation tofauti katika Zoezi$\PageIndex{3}$.
$ n$	\ (x_n)	$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$
0	1	-2
1	1.1	$ y_1=y_0+hf(x_0,y_0)=−1.5$
2	1.2	$ y_2=y_1+hf(x_1,y_1)=−1.1419$
3	1.3	$ y_3=y_2+hf(x_2,y_2)=−0.8387$
4	1.4	$ y_4=y_3+hf(x_3,y_3)=−0.5487$
5	1.5	$ y_5=y_4+hf(x_4,y_4)=−0.2442$
6	1.6	$ y_6=y_5+hf(x_5,y_5)=0.0993$
7	1.7	$ y_7=y_6+hf(x_6,y_6)=0.5099$
8	1.8	$ y_8=y_7+hf(x_7,y_7)=1.0272$
9	1.9	$ y_9=y_8+hf(x_8,y_8)=1.7159$
10	2	$ y_{10}=y_9+hf(x_9,y_9)=2.6962$

Dhana muhimu

Shamba la mwelekeo ni kitu cha hisabati kinachotumiwa kuwakilisha graphically ufumbuzi wa equation tofauti ya kwanza.
Njia ya Euler ni mbinu ya namba ambayo inaweza kutumika kwa takriban ufumbuzi wa equation tofauti.

Mlinganyo muhimu

Njia ya Euler

$ x_n=x_0+nh$

$ y_n=y_{n−1}+hf(x_{n−1},y_{n−1})$, ukubwa wa hatua$ h$ ni wapi

faharasa

ufumbuzi usio na utulivu wa nusu imara: $ y=k$kama si asymptotically imara wala asymptotically imara

ufumbuzi usio na utulivu: $ y=k$ikiwa kuna$ ε>0$ vile kwamba kwa thamani yoyote ufumbuzi$ c∈(k−ε,\, k+ε)$ wa tatizo la thamani ya awali$ y′=f(x,y),\; y(x_0)=c$ unakaribia$ k$ kama$ x$ inakaribia infinity

ufumbuzi usio na uhakika: $ y=k$ikiwa kuna$ ε>0$ vile kwamba kwa thamani yoyote ufumbuzi$ c∈(k−ε,\, k+ε)$ wa tatizo la thamani ya awali haujafikia$ y′=f(x,y),\; y(x_0)=c$ kamwe$ k$ kama$ x$ inakaribia infinity

uwanja wa mwelekeo (uwanja wa mteremko): kitu cha hisabati kilichotumiwa kuwakilisha graphically ufumbuzi wa equation tofauti ya kwanza; katika kila hatua katika uwanja wa mwelekeo, sehemu ya mstari inaonekana ambayo mteremko ni sawa na mteremko wa suluhisho la equation tofauti inayopitia hatua hiyo

ufumbuzi wa usawa: ufumbuzi wowote wa equation tofauti ya fomu$ y=c,$ ambapo$ c$ ni mara kwa mara

Njia ya Euler: mbinu ya namba inayotumiwa kufikia ufumbuzi wa tatizo la thamani ya awali

ufumbuzi curve: safu iliyowekwa kwenye uwanja wa mwelekeo unaofanana na suluhisho la tatizo la thamani ya awali inayopitia hatua fulani katika uwanja wa uongozi

ukubwa wa hatua: increment hh kwamba ni aliongeza kwa thamani xx katika kila hatua katika Method Euler

Wachangiaji na Majina

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) edited this section to adjust the explanation of equilibrium points in the example shown in Figures $ \PageIndex{4}$ - $ \PageIndex{6}$. He also created these figures.

Ufafanuzi: Uwanja wa Mwelekeo (Uwanja wa S

Zoezi\(\PageIndex{1}\)

Ufafanuzi: E usawa Solutions

Ufafanuzi: Ufumbuzi usio imara, usio na uhakika na Semi-Imara

Mfano\( \PageIndex{1}\): Stability of an Equilibrium Solution

Zoezi\(\PageIndex{2}\)

Njia ya Euler

Mfano\( \PageIndex{2}\): Using Euler’s Method

Zoezi\(\PageIndex{3}\)

\( n\)	0	1	2	3	4	5
\( x_n\)	-1	-0.9	-0.8	-0.7	-0.6	-0.5
\( y_n\)	2	1.7	1.492	1.3334	1.2046	1.0955
\( n\)	6	7	8	9	10
\( x_n\)	-0.4	-0.3	-0.2	-0.1	0
\( y_n\)	1.0004	1.9164	1.8414	1.7746	1.7156

\( n\)	\ (x_n)	\( y_n=y_{n−1}+hf(x_{n−1},y_{n−1})\)
0	1	-2
1	1.1	\( y_1=y_0+hf(x_0,y_0)=−1.5\)
2	1.2	\( y_2=y_1+hf(x_1,y_1)=−1.1419\)
3	1.3	\( y_3=y_2+hf(x_2,y_2)=−0.8387\)
4	1.4	\( y_4=y_3+hf(x_3,y_3)=−0.5487\)
5	1.5	\( y_5=y_4+hf(x_4,y_4)=−0.2442\)
6	1.6	\( y_6=y_5+hf(x_5,y_5)=0.0993\)
7	1.7	\( y_7=y_6+hf(x_6,y_6)=0.5099\)
8	1.8	\( y_8=y_7+hf(x_7,y_7)=1.0272\)
9	1.9	\( y_9=y_8+hf(x_8,y_8)=1.7159\)
10	2	\( y_{10}=y_9+hf(x_9,y_9)=2.6962\)