8.1: Misingi ya Ulinganisho tofauti

Last updated
Save as PDF

Page ID: 178684

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Tambua utaratibu wa equation tofauti.
Eleza nini maana ya ufumbuzi wa equation tofauti.
Tofautisha kati ya suluhisho la jumla na suluhisho fulani la usawa tofauti.
Tambua tatizo la thamani ya awali.
Tambua kama kazi iliyotolewa ni suluhisho la equation tofauti au tatizo la thamani ya awali.

Calculus ni hisabati ya mabadiliko, na viwango vya mabadiliko vinaonyeshwa na derivatives. Hivyo, mojawapo ya njia za kawaida za kutumia calculus ni kuanzisha equation iliyo\(y=f(x)\) na kazi isiyojulikana na derivative yake, inayojulikana kama equation tofauti. Kutatua milinganyo hiyo mara nyingi hutoa taarifa kuhusu jinsi kiasi kinavyobadilika na mara nyingi hutoa ufahamu wa jinsi na kwa nini mabadiliko yanatokea.

Mbinu za kutatua equations tofauti zinaweza kuchukua aina nyingi tofauti, ikiwa ni pamoja na ufumbuzi wa moja kwa moja, matumizi ya grafu, au mahesabu ya kompyuta. Tunaanzisha mawazo makuu katika sura hii na kuelezea kwa undani zaidi baadaye katika kozi. Katika sehemu hii tunajifunza ni nini usawa tofauti, jinsi ya kuthibitisha ufumbuzi wao, mbinu zingine zinazotumiwa kutatua, na baadhi ya mifano ya equations ya kawaida na muhimu.

Ulinganifu wa jumla

Fikiria equation\(y′=3x^2,\) ambayo ni mfano wa equation tofauti kwa sababu ni pamoja na derivative. Kuna uhusiano kati ya vigezo\(x\) na\(y:y\) ni kazi haijulikani ya\(x\). Zaidi ya hayo, upande wa kushoto wa equation ni derivative ya\(y\). Kwa hiyo tunaweza kutafsiri equation hii kama ifuatavyo: Anza na kazi fulani\(y=f(x)\) na kuchukua derivative yake. Jibu lazima iwe sawa na\(3x^2\). Ni kazi gani ina derivative ambayo ni sawa na\(3x^2\)? Kazi moja ni\(y=x^3\), hivyo kazi hii inachukuliwa kuwa suluhisho la equation tofauti.

Ufafanuzi: equation tofauti

Equation tofauti ni equation inayohusisha kazi isiyojulikana\(y=f(x)\) na moja au zaidi ya derivatives yake. Suluhisho la equation tofauti ni kazi\(y=f(x)\) ambayo inatimiza equation tofauti wakati\(f\) na derivatives yake ni kubadilishwa katika equation.

Nenda kwenye tovuti hii ili uchunguze zaidi juu ya mada hii.

Baadhi ya mifano ya usawa tofauti na ufumbuzi wao huonekana katika Jedwali\(\PageIndex{1}\).

Jedwali\(\PageIndex{1}\): Mifano ya Ulinganisho tofauti na Ufumbuzi wao
Mlinganyo	Suluhisho
\(y'=2x\)	\(y=x^2\)
\(y'+3y=6x+11\)	\(y=e^{−3x}+2x+3\)
\(y''−3y'+2y=24e^{−2x}\)	\(y=3e^x−4e^{2x}+2e^{−2x}\)

Kumbuka kuwa suluhisho la equation tofauti sio ya kipekee, hasa kwa sababu derivative ya mara kwa mara ni sifuri. Kwa mfano, pia\(y=x^2+4\) ni ufumbuzi wa equation kwanza tofauti katika Jedwali\(\PageIndex{1}\). Tutarudi wazo hili baadaye baadaye katika sehemu hii. Kwa sasa, hebu kuzingatia nini maana kwa ajili ya kazi kuwa suluhisho la equation tofauti.

Mfano\(\PageIndex{1}\): Verifying Solutions of Differential Equations

Thibitisha kwamba kazi\(y=e^{−3x}+2x+3\) ni suluhisho la usawa tofauti\(y′+3y=6x+11\).

Suluhisho

Ili kuthibitisha suluhisho, sisi kwanza tunahesabu\(y′\) kutumia utawala wa mnyororo kwa derivatives. Hii inatoa\(y′=−3e^{−3x}+2\). Kisha sisi badala\(y\) na\(y′\) upande wa kushoto wa equation tofauti:

\((−3e^{−2x}+2)+3(e^{−2x}+2x+3).\)

Maneno yanayotokana yanaweza kuwa rahisi kwa kusambaza kwanza ili kuondokana na mabano, kutoa

\(−3e^{−2x}+2+3e^{−2x}+6x+9.\)

Kuchanganya kama maneno husababisha kujieleza\(6x+11\), ambayo ni sawa na upande wa kulia wa equation tofauti. Matokeo haya inathibitisha kwamba\(y=e^{−3x}+2x+3\) ni suluhisho la equation tofauti.

Zoezi\(\PageIndex{1}\)

Thibitisha kwamba\(y=2e^{3x}−2x−2\) ni suluhisho la equation tofauti\(y′−3y=6x+4.\)

Kidokezo: Kwanza hesabu\(y′\) kisha\(y′\)\(y\) ubadilishe wote na upande wa kushoto.

Ni rahisi kufafanua sifa za equations tofauti ambazo zinawezesha kuzungumza juu yao na kuziweka. Tabia ya msingi ya equation tofauti ni utaratibu wake.

Ufafanuzi: utaratibu wa equation tofauti

Utaratibu wa equation tofauti ni utaratibu wa juu wa derivative yoyote ya kazi isiyojulikana inayoonekana katika equation.

Mfano\(\PageIndex{2}\): Identifying the Order of a Differential Equation

Derivative ya juu katika equation ni\(y′\),

Nini utaratibu wa kila moja ya equations tofauti zifuatazo?

\(y′−4y=x^2−3x+4\)
\(x^2y'''−3xy''+xy′−3y=\sin x\)
\(\frac{4}{x}y^{(4)}−\frac{6}{x^2}y''+\frac{12}{x^4}y=x^3−3x^2+4x−12\)

Suluhisho

derivative ya juu katika equation ni\(y′\), hivyo ili ni\(1\).
derivative ya juu katika equation ni\(y'''\), hivyo ili ni\(3\).
derivative ya juu katika equation ni\(y^{(4)}\), hivyo ili ni\(4\).

Zoezi\(\PageIndex{2}\)

Nini utaratibu wa equation tofauti yafuatayo?

\((x^4−3x)y^{(5)}−(3x^2+1)y′+3y=\sin x\cos x\)

Kidokezo: Je, ni derivative ya juu zaidi katika equation?

Jibu: \(5\)

Ufumbuzi Mkuu na Maalum

Tumebainisha kuwa equation tofauti\(y′=2x\) ina angalau ufumbuzi mbili:\(y=x^2\) na\(y=x^2+4\). Tofauti pekee kati ya ufumbuzi huu wawili ni muda wa mwisho, ambao ni mara kwa mara. Nini kama muda wa mwisho ni tofauti mara kwa mara? Je, maneno haya bado kuwa suluhisho la equation tofauti? Kwa kweli, kazi yoyote ya fomu\(y=x^2+C\), ambapo\(C\) inawakilisha mara kwa mara yoyote, ni suluhisho pia. Sababu ni kwamba derivative ya\(x^2+C\) ni\(2x\), bila kujali thamani ya\(C\). Inaweza kuonyeshwa kuwa suluhisho lolote la usawa huu tofauti lazima uwe wa fomu\(y=x^2+C\). Huu ni mfano wa suluhisho la jumla kwa equation tofauti. Grafu ya baadhi ya ufumbuzi huu hutolewa katika Kielelezo\(\PageIndex{1}\). (Kumbuka: katika grafu hii tulitumia hata maadili ya integer kwa C kuanzia kati\(−4\) na\(4\). Kwa kweli, hakuna kizuizi juu ya thamani ya\(C\); inaweza kuwa integer au la.)

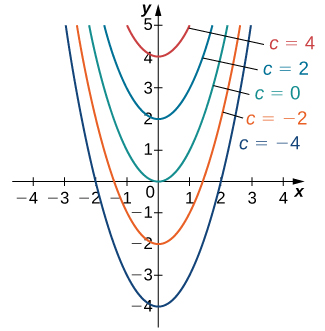
Grafu ya familia ya ufumbuzi wa equation tofauti y' = 2 x, ambayo ni ya fomu y = x ^ 2 + C. parabolas hutolewa kwa maadili ya C: -4, -2, 0, 2, na 4. — Kielelezo\(\PageIndex{1}\): Familia ya ufumbuzi wa equation tofauti\(y′=2x.\)

Katika mfano huu, sisi ni huru kuchagua suluhisho lolote tunayotaka; kwa mfano,\(y=x^2−3\) ni mwanachama wa familia ya ufumbuzi wa equation hii tofauti. Hii inaitwa suluhisho fulani kwa equation tofauti. Suluhisho fulani linaweza kutambuliwa kwa pekee ikiwa tunapewa maelezo ya ziada kuhusu tatizo.

Mfano\(\PageIndex{3}\): Finding a Particular Solution

Kupata ufumbuzi maalum kwa equation tofauti\(y′=2x\) kupita katika hatua\((2,7)\).

Suluhisho

Kazi yoyote ya fomu\(y=x^2+C\) ni suluhisho la equation hii tofauti. Kuamua thamani ya\(C\), sisi badala ya maadili\(x=2\) na\(y=7\) katika equation hii na kutatua kwa\(C\):

\[ \begin{align*} y =x^2+C \\[4pt] 7 =2^2+C \\[4pt] =4+C \\[4pt] C =3. \end{align*}\]

Kwa hiyo ufumbuzi fulani unaopitia hatua\((2,7)\) ni\(y=x^2+3\).

Zoezi\(\PageIndex{3}\)

Kupata ufumbuzi maalum kwa equation tofauti

\[ y′=4x+3 \nonumber \]

kupitia hatua\((1,7),\) iliyotolewa kuwa\(y=2x^2+3x+C\) ni suluhisho la jumla kwa equation tofauti.

Kidokezo: Kwanza mbadala\(x=1\) na\(y=7\) katika equation, kisha kutatua kwa\(C\).

Jibu: \[ y=2x^2+3x+2 \nonumber \]

Matatizo ya Thamani ya awali

Kawaida equation tofauti iliyotolewa ina idadi isiyo na kipimo cha ufumbuzi, kwa hiyo ni kawaida kuuliza ni nani tunayotaka kutumia. Ili kuchagua suluhisho moja, habari zaidi inahitajika. Maelezo maalum ambayo yanaweza kuwa na manufaa ni thamani ya awali, ambayo ni jozi iliyoamriwa ambayo hutumiwa kupata suluhisho fulani.

Equation tofauti pamoja na maadili moja au zaidi ya awali inaitwa tatizo la thamani ya awali. Utawala wa jumla ni kwamba idadi ya maadili ya awali inahitajika kwa tatizo la thamani ya awali ni sawa na utaratibu wa equation tofauti. Kwa mfano, kama tuna equation tofauti\(y′=2x\), basi\(y(3)=7\) ni thamani ya awali, na wakati kuchukuliwa pamoja, equations hizi fomu ya awali ya thamani tatizo. Equation tofauti\(y''−3y′+2y=4e^x\) ni utaratibu wa pili, hivyo tunahitaji maadili mawili ya awali. Kwa matatizo ya thamani ya awali ya utaratibu mkubwa kuliko moja, thamani sawa inapaswa kutumika kwa kutofautiana kwa kujitegemea. Mfano wa maadili ya awali kwa equation hii ya pili ili itakuwa\(y(0)=2\) na maadili\(y′(0)=−1.\) haya mawili ya awali pamoja na equation tofauti huunda tatizo la thamani ya awali. Matatizo haya ni hivyo jina lake kwa sababu mara nyingi variable huru katika kazi haijulikani ni\(t\), ambayo inawakilisha wakati. Hivyo, thamani ya\(t=0\) inawakilisha mwanzo wa tatizo.

Mfano\(\PageIndex{4}\): Verifying a Solution to an Initial-Value Problem

Thibitisha kwamba kazi\(y=2e^{−2t}+e^t\) ni suluhisho la tatizo la thamani ya awali

\[ y′+2y=3e^t, \quad y(0)=3.\nonumber \]

Suluhisho

Kwa kazi ya kukidhi tatizo awali thamani, ni lazima kukidhi wote equation tofauti na hali ya awali. Ili kuonyesha kwamba\(y\) inatimiza usawa tofauti, tunaanza kwa kuhesabu\(y′\). Hii inatoa\(y′=−4e^{−2t}+e^t\). Kisha sisi badala ya wote\(y\) na\(y′\) upande wa kushoto wa equation tofauti na kurahisisha:

\[ \begin{align*} y′+2y &=(−4e^{−2t}+e^t)+2(2e^{−2t}+e^t) \\[4pt] &=−4e^{−2t}+e^t+4e^{−2t}+2e^t =3e^t. \end{align*}\]

Hii ni sawa na upande wa kulia wa equation tofauti, hivyo\(y=2e^{−2t}+e^t\) hutatua equation tofauti. Ifuatayo tunahesabu\(y(0)\):

\[ y(0)=2e^{−2(0)}+e^0=2+1=3. \nonumber \]

Matokeo haya inathibitisha thamani ya awali. Kwa hiyo kazi iliyotolewa inatimiza tatizo la thamani ya awali.

Zoezi\(\PageIndex{4}\)

Thibitisha kwamba\(y=3e^{2t}+4\sin t\) ni suluhisho la tatizo la thamani ya awali

\[ y′−2y=4\cos t−8\sin t,y(0)=3. \nonumber \]

Kidokezo: Kwanza kuthibitisha kwamba\(y\) kutatua equation tofauti. Kisha angalia thamani ya awali.

Katika Mfano\(\PageIndex{4}\), tatizo la thamani ya awali lilikuwa na sehemu mbili. Sehemu ya kwanza ilikuwa tofauti equation\(y′+2y=3e^x\), na sehemu ya pili ilikuwa thamani ya awali milinganyo\(y(0)=3.\) hizi mbili pamoja sumu tatizo awali thamani.

Vile vile ni kweli kwa ujumla. Tatizo la thamani ya awali litakuwa na sehemu mbili: equation tofauti na hali ya awali. Equation tofauti ina familia ya ufumbuzi, na hali ya awali huamua thamani ya\(C\). Familia ya ufumbuzi wa equation tofauti katika Mfano\(\PageIndex{4}\) hutolewa na familia\(y=2e^{−2t}+Ce^t.\) hii ya ufumbuzi ni inavyoonekana katika Kielelezo\(\PageIndex{2}\), na ufumbuzi fulani\(y=2e^{−2t}+e^t\) kinachoitwa.

Grafu ya familia ya ufumbuzi wa equation tofauti y+2 y = 3 e ^ t, ambayo ni ya fomu y = 2 e ^ (-2 t) + C e ^ t. matoleo na C = 1, 0.5, na -0.2 yanaonyeshwa, kati ya wengine sio lebo. Kwa maadili yote ya C, kazi huongezeka kwa kasi kwa t <0 kama t inakwenda infinity hasi. Kwa C — Kielelezo\(\PageIndex{2}\): Familia ya ufumbuzi wa equation tofauti\(y′+2y=3e^t\). Suluhisho fulani\(y=2e^{−2t}+e^t\) linaandikwa.

Mfano\(\PageIndex{5}\): Solving an Initial-value Problem

Tatua tatizo la thamani ya awali:

\[ y′=3e^x+x^2−4,y(0)=5. \nonumber \]

Suluhisho

Hatua ya kwanza katika kutatua tatizo hili la thamani ya awali ni kupata familia ya jumla ya ufumbuzi. Ili kufanya hivyo, tunapata antiderivative ya pande zote mbili za equation tofauti

\[∫y′\,dx=∫(3e^x+x^2−4)\,dx, \nonumber \]

yaani,

\(y+C_1=3e^x+\frac{1}{3}x^3−4x+C_2\).

Tunaweza kuunganisha pande zote mbili kwa sababu neno y linaonekana yenyewe. Kumbuka kwamba kuna mara mbili ushirikiano constants:\(C_1\) na\(C_2\). Kutatua equation hii kwa\(y\) anatoa

\(y=3e^x+\frac{1}{3}x^3−4x+C_2−C_1.\)

Kwa sababu\(C_1\) na\(C_2\) wote wawili constants, pia\(C_2−C_1\) ni mara kwa mara. Kwa hiyo tunaweza kufafanua\(C=C_2−C_1,\) ambayo inaongoza kwa equation

\(y=3e^x+\frac{1}{3}x^3−4x+C.\)

Halafu tunaamua thamani ya\(C\). Ili kufanya hivyo, sisi badala\(x=0\) na\(y=5\) katika equation hii na kutatua kwa\(C\):

\[ \begin{align*} 5 &=3e^0+\frac{1}{3}0^3−4(0)+C \\[4pt] 5 &=3+C \\[4pt] C&=2 \end{align*}. \nonumber \]

Sasa tunabadilisha thamani\(C=2\) katika usawa wa jumla. Suluhisho la tatizo la thamani ya awali ni\(y=3e^x+\frac{1}{3}x^3−4x+2.\)

Uchambuzi

Tofauti kati ya suluhisho la jumla na suluhisho fulani ni kwamba suluhisho la jumla linahusisha familia ya kazi, ama wazi au kwa uwazi, ya kutofautiana kwa kujitegemea. Thamani ya awali au maadili huamua ufumbuzi fulani katika familia ya ufumbuzi hutimiza hali zinazohitajika.

Zoezi\(\PageIndex{5}\)

Tatua tatizo la thamani ya awali

\[ y′=x^2−4x+3−6e^x,y(0)=8. \nonumber \]

Kidokezo: Kwanza kuchukua antiderivative ya pande zote mbili za equation tofauti. Kisha mbadala\(x=0\) na\(y=8\) katika equation kusababisha na kutatua kwa\(C\).

Jibu: \(y=\frac{1}{3}x^3−2x^2+3x−6e^x+14\)

Katika maombi ya fizikia na uhandisi, mara nyingi tunazingatia nguvu zinazofanya kitu, na kutumia habari hii kuelewa mwendo unaoweza kutokea. Kwa mfano, kama tunaanza na kitu kwenye uso wa Dunia, nguvu ya msingi inayofanya juu ya kitu hicho ni mvuto. Wafizikia na wahandisi wanaweza kutumia habari hii, pamoja na sheria ya pili ya mwendo wa Newton (katika fomu ya equation\(F=ma\), ambapo\(F\) inawakilisha nguvu,\(m\) inawakilisha wingi, na\(a\) inawakilisha kuongeza kasi), ili kupata equation ambayo inaweza kutatuliwa.

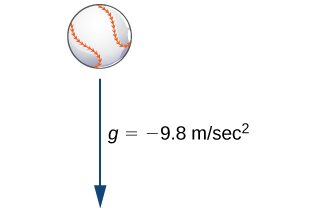
picha ya baseball na mshale chini yake akizungumzia chini. Mshale umeandikwa g = -9.8 m/sec ^ 2. — Kielelezo\(\PageIndex{3}\): Kwa baseball kuanguka katika hewa, nguvu pekee inayofanya juu yake ni mvuto (kupuuza upinzani wa hewa).

Katika Kielelezo\(\PageIndex{3}\) sisi kudhani kwamba nguvu tu kaimu baseball ni nguvu ya mvuto. Dhana hii inapuuza upinzani wa hewa. (Nguvu kutokana na upinzani wa hewa inachukuliwa katika majadiliano ya baadaye.) Kuongezeka kwa sababu ya mvuto kwenye uso wa Dunia, g, ni takriban\(9.8\,\text{m/s}^2\). Tunaanzisha sura ya kumbukumbu, ambapo uso wa dunia una urefu wa mita 0. Hebu\(v(t)\) kuwakilisha kasi ya kitu katika mita kwa pili. Ikiwa\(v(t)>0\), mpira unaongezeka, na ikiwa\(v(t)<0\), mpira unaanguka (Kielelezo).

picha ya baseball na mshale juu yake akizungumzia juu na mshale chini yake akizungumzia chini. Mshale unaoelekeza juu umeandikwa v (t) — Kielelezo\(\PageIndex{4}\): Uwezekano kasi kwa kuinuka/kuanguka baseball.

Lengo letu ni kutatua kwa kasi\(v(t)\) wakati wowote\(t\). Ili kufanya hivyo, tunaanzisha tatizo la thamani ya awali. Tuseme wingi wa mpira ni\(m\), ambapo\(m\) hupimwa kwa kilo. Tunatumia sheria ya pili ya Newton, ambayo inasema kwamba nguvu inayofanya kitu ni sawa na mara zake za uzito kasi yake\((F=ma)\). Kuharakisha ni derivative ya kasi, hivyo\(a(t)=v′(t)\). Kwa hiyo nguvu inayofanya baseball inapewa na\(F=mv′(t)\). Hata hivyo, nguvu hii lazima iwe sawa na nguvu ya mvuto inayofanya kitu, ambacho (tena kwa kutumia sheria ya pili ya Newton) hutolewa na\(F_g=−mg\), kwani nguvu hii inachukua mwelekeo wa chini. Kwa hiyo tunapata equation\(F=F_g\), ambayo inakuwa\(mv′(t)=−mg\). Kugawanya pande zote mbili za equation na\(m\) anatoa equation

\[ v′(t)=−g. \nonumber \]

Kumbuka kwamba equation hii tofauti inabakia sawa bila kujali wingi wa kitu.

Sasa tunahitaji thamani ya awali. Kwa sababu sisi ni kutatua kwa kasi, ni mantiki katika mazingira ya tatizo kudhani kwamba tunajua kasi ya awali, au kasi kwa wakati\(t=0.\) Hii ni ulionyehsa na\(v(0)=v_0.\)

Mfano\(\PageIndex{6}\): Velocity of a Moving Baseball

Baseball inatupwa juu kutoka urefu wa\(3\) mita juu ya uso wa dunia na kasi ya awali ya\(10\) m/s, na nguvu pekee inayofanya juu yake ni mvuto. Mpira una wingi wa\(0.15\) kilo kwenye uso wa dunia.

Kupata kasi\(v(t)\) ya basevall kwa wakati\(t\).
Je! Ni kasi gani baada ya\(2\) sekunde?

Suluhisho

a Kutoka majadiliano yaliyotangulia, usawa tofauti unaotumika katika hali hii ni

\(v′(t)=−g,\)

wapi\(g=9.8\, \text{m/s}^2\). Hali ya awali ni\(v(0)=v_0\), wapi\(v_0=10\) m/s Kwa hiyo tatizo la thamani ya awali ni\(v′(t)=−9.8\,\text{m/s}^2,\,v(0)=10\) m/s.

Hatua ya kwanza katika kutatua tatizo hili la thamani ya awali ni kuchukua antiderivative ya pande zote mbili za equation tofauti. Hii inatoa

\[\int v′(t)\,dt=∫−9.8\,dt \nonumber \]

\(v(t)=−9.8t+C.\)

Hatua inayofuata ni kutatua\(C\). Ili kufanya hivyo, mbadala\(t=0\) na\(v(0)=10\):

\[ \begin{align*} v(t) &=−9.8t+C \\[4pt] v(0) &=−9.8(0)+C \\[4pt] 10 &=C. \end{align*}\]

Kwa hiyo,\(C=10\) na kazi ya kasi hutolewa na\(v(t)=−9.8t+10.\)

b Ili kupata kasi baada ya\(2\) sekunde, mbadala\(t=2\) katika\(v(t)\).

\[ \begin{align*} v(t)&=−9.8t+10 \\[4pt] v(2)&=−9.8(2)+10 \\[4pt] v(2) &=−9.6\end{align*}\]

Vitengo vya kasi ni mita kwa pili. Kwa kuwa jibu ni hasi, kitu kinaanguka kwa kasi ya\(9.6\) m/s.

Zoezi\(\PageIndex{6}\)

Tuseme mwamba huanguka kutoka kupumzika kutoka urefu wa\(100\) mita na nguvu pekee inayofanya juu yake ni mvuto. Kupata equation kwa kasi\(v(t)\) kama kazi ya muda, kipimo katika mita kwa sekunde.

Kidokezo: Je! Ni kasi gani ya awali ya mwamba? Tumia hii kwa usawa tofauti katika Mfano\(\PageIndex{6}\) ili kuunda tatizo la thamani ya awali, halafu tatua\(v(t)\).

Jibu: \(v(t)=−9.8t\)

Swali la asili la kuuliza baada ya kutatua aina hii ya tatizo ni jinsi kitu kitakavyokuwa juu ya uso wa Dunia kwa wakati fulani. Hebu\(s(t)\) kuashiria urefu juu ya uso wa Dunia wa kitu, kipimo kwa mita. Kwa sababu kasi ni derivative ya nafasi (katika kesi hii urefu), dhana hii inatoa equation\(s′(t)=v(t)\). Thamani ya awali ni muhimu; katika kesi hii urefu wa awali wa kitu hufanya vizuri. Hebu urefu wa awali utolewe na equation\(s(0)=s_0\). Pamoja mawazo haya kutoa awali thamani tatizo

\[ s′(t)=v(t),s(0)=s_0. \nonumber \]

Ikiwa kazi ya kasi inajulikana, basi inawezekana kutatua kwa kazi ya msimamo pia.

Mfano\(\PageIndex{7}\): Height of a Moving Baseball

baseball ni kutupwa juu kutoka urefu wa\(3\) mita juu ya uso wa dunia na kasi ya awali ya\(10m/s\), na nguvu tu kaimu juu yake ni mvuto. Mpira una wingi wa\(0.15\) kilo kwenye uso wa dunia.

Kupata nafasi\(s(t)\) ya baseball kwa wakati\(t\).
Urefu wake baada ya\(2\) sekunde ni nini?

Suluhisho

Tayari tunajua kasi kazi kwa tatizo hili ni\(v(t)=−9.8t+10\). Urefu wa awali wa baseball ni\(3\) mita, hivyo\(s_0=3\). Kwa hiyo tatizo la thamani ya awali kwa mfano huu ni

Ili kutatua tatizo la thamani ya awali, tunapata kwanza antiderivatives:

\[∫s′(t)\,dt=∫(−9.8t+10)\,dt \nonumber \]

\(s(t)=−4.9t^2+10t+C.\)

Kisha sisi badala\(t=0\) na kutatua kwa\(C\):

\(s(t)=−4.9t^2+10t+C\)

\(s(0)=−4.9(0)^2+10(0)+C\)

\(3=C\).

Kwa hiyo, kazi ya msimamo ni\(s(t)=−4.9t^2+10t+3.\)

b. urefu wa baseball baada ya\(2\) sec hutolewa na\(s(2):\)

\(s(2)=−4.9(2)^2+10(2)+3=−4.9(4)+23=3.4.\)

Kwa hiyo baseball ni\(3.4\) mita juu ya uso wa dunia baada ya\(2\) sekunde. Ni muhimu kutambua kwamba wingi wa mpira umefutwa kabisa katika mchakato wa kutatua tatizo.

Dhana muhimu

Equation tofauti ni equation inayohusisha kazi\(y=f(x)\) na moja au zaidi ya derivatives yake. Suluhisho ni kazi\(y=f(x)\) ambayo inatimiza equation tofauti wakati\(f\) na derivatives yake ni kubadilishwa katika equation.
Utaratibu wa equation tofauti ni utaratibu wa juu wa derivative yoyote ya kazi isiyojulikana inayoonekana katika equation.
Equation tofauti pamoja na thamani ya awali inaitwa tatizo la thamani ya awali. Ili kutatua tatizo la thamani ya awali, kwanza pata suluhisho la jumla kwa usawa tofauti, kisha ueleze thamani ya mara kwa mara. Matatizo ya thamani ya awali yana maombi mengi katika sayansi na uhandisi.

faharasa

equation tofauti: equation kuwashirikisha kazi\(y=y(x)\) na moja au zaidi ya derivatives yake

suluhisho la jumla (au familia ya ufumbuzi): seti nzima ya ufumbuzi wa equation tofauti iliyotolewa

thamani ya awali: thamani au seti ya maadili ambayo suluhisho la equation tofauti hutimiza kwa thamani ya kudumu ya kutofautiana kwa kujitegemea

kasi ya awali: kasi kwa wakati\(t=0\)

tatizo la thamani ya awali: equation tofauti pamoja na thamani ya awali au maadili

utaratibu wa equation tofauti: utaratibu wa juu wa derivative yoyote ya kazi haijulikani kwamba inaonekana katika equation

ufumbuzi maalum: mwanachama wa familia ya ufumbuzi wa equation tofauti kwamba satisfies hali fulani ya awali

ufumbuzi wa equation tofauti: kazi\(y=f(x)\) ambayo satisfies kutolewa tofauti equation