7.4E: Mazoezi ya Sehemu ya 7.4

Tumia uharibifu wa sehemu ya sehemu (au mbinu rahisi) ili kuelezea kazi ya busara kama jumla au tofauti ya maneno mawili au zaidi ya busara.

1)\(\dfrac{1}{(x−3)(x−2)}\)

2)\(\dfrac{x^2+1}{x(x+1)(x+2)}\)

Jibu

\(\dfrac{x^2+1}{x(x+1)(x+2)} \quad = \quad −\dfrac{2}{x+1}+\dfrac{5}{2(x+2)}+\dfrac{1}{2x}\)

3)\(\dfrac{1}{x^3−x}\)

4)\(\dfrac{3x+1}{x^2}\)

Jibu

\(\dfrac{3x+1}{x^2} \quad = \quad \dfrac{1}{x^2}+\dfrac{3}{x}\)

5)\(\dfrac{3x^2}{x^2+1}\) (kidokezo: Tumia mgawanyiko wa muda mrefu kwanza.)

6)\(\dfrac{2x^4}{x^2−2x}\)

Jibu

\(\dfrac{2x^4}{x^2−2x} \quad = \quad 2x^2+4x+8+\dfrac{16}{x−2}\)

7)\(\dfrac{1}{(x−1)(x^2+1)}\)

8)\(\dfrac{1}{x^2(x−1)}\)

Jibu

\(\dfrac{1}{x^2(x−1)} \quad = \quad −\dfrac{1}{x^2}−\dfrac{1}{x}+\dfrac{1}{x−1}\)

9)\(\dfrac{x}{x^2−4}\)

10)\(\dfrac{1}{x(x−1)(x−2)(x−3)}\)

Jibu

\(\dfrac{1}{x(x−1)(x−2)(x−3)} \quad = \quad −\dfrac{1}{2(x−2)}+\dfrac{1}{2(x−1)}−\dfrac{1}{6x}+\dfrac{1}{6(x−3)}\)

11)\(\dfrac{1}{x^4−1}=\dfrac{1}{(x+1)(x−1)(x^2+1)}\)

12)\(\dfrac{3x^2}{x^3−1}=\dfrac{3x^2}{(x−1)(x^2+x+1)}\)

Jibu

\(\dfrac{3x^2}{x^3−1} \quad = \quad \dfrac{1}{x−1}+\dfrac{2x+1}{x^2+x+1}\)

13)\(\dfrac{2x}{(x+2)^2}\)

14)\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2}\)

Jibu

\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2} \quad = \quad \dfrac{2}{x+1}+\dfrac{x}{x^2+4}−\dfrac{1}{(x^2+4)^2}\)

Katika mazoezi ya 15 - 25, tumia njia ya sehemu ndogo ili kutathmini kila moja ya vipengele vifuatavyo.

15)\(\displaystyle ∫\frac{dx}{(x−3)(x−2)}\)

16)\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx\)

Jibu

\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx \quad = \quad 2\ln|x+4|+\ln|x-2|+C = \ln\left| (x+4)^2(x-2) \right| + C\)

17)\(\displaystyle ∫\frac{dx}{x^3−x}\)

18)\(\displaystyle ∫\frac{x}{x^2−4}\,dx\)

Jibu

Kumbuka kwamba huhitaji sehemu ndogo hapa. Tunatumia rahisi\(u\) -badala.
\(\displaystyle ∫\frac{x}{x^2−4}\,dx \quad = \quad \tfrac{1}{2}\ln|4−x^2|+C\)

19)\(\displaystyle ∫\frac{dx}{x(x−1)(x−2)(x−3)}\)

20)\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx\)

Jibu

Kumbuka kwamba kwa kuwa kiwango cha nambari ni sawa na kiwango cha denominator, tunahitaji kuanza na mgawanyiko mrefu.
Kisha kumbuka kwamba tutahitaji kutumia kukamilisha mraba kuendelea kwani hatuwezi kuzingatia trinomial katika denominator.
\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx \quad = \quad 2\left(x+\tfrac{1}{3}\arctan\left(\frac{1+x}{3}\right)\right)+C\)

21)\(\displaystyle ∫\frac{dx}{x^2−5x+6}\)

22)\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx\)

Jibu

\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx \quad = \quad 2\ln|x|−3\ln|1+x|+C = \ln\left| \frac{x^2}{(1+x)^3} \right|+C\)

23)\(\displaystyle ∫\frac{2}{x^2−x−6}\,dx\)

24)\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8}\)

Jibu

\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8} \quad = \quad \tfrac{1}{16}\left(−\frac{4}{−2+x}−\ln|−2+x|+\ln|2+x|\right)+C = \tfrac{1}{16}\left(−\frac{4}{−2+x}+\ln\left| \frac{x+2}{x-2} \right|\right)+C\)

25)\(\displaystyle ∫\frac{dx}{x^4−10x^2+9}\)

Katika mazoezi 26 - 29, tathmini integrals na sababu zisizoweza kupunguzwa kwa quadratic katika denominators.

26)\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx\)

Jibu

\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx \quad = \quad \tfrac{1}{30}(−2\sqrt{5}\arctan\left[\frac{1+x}{\sqrt{5}}\right]+2\ln|−4+x|−\ln|6+2x+x^2|)+C\)

27)\(\displaystyle ∫\frac{x^2}{x^3−x^2+4x−4}\,dx\)

28)\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx\)

Jibu

Kumbuka kwamba tunahitaji kutumia mgawanyiko mrefu kwanza, kwa kuwa kiwango cha nambari ni kubwa kuliko kiwango cha denominator.
\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx \quad = \quad −\frac{3}{x}+4\ln|x+2|+x+C\)

29)\(\displaystyle ∫\frac{x}{(x−1)(x^2+2x+2)^2}\,dx\)

Katika mazoezi 30 - 32, tumia njia ya sehemu ndogo ili kutathmini integrals.

30)\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx\)

Jibu

\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx \quad = \quad −\ln|3−x|+\tfrac{1}{2}\ln|x^2+4|+C\)

31)\(\displaystyle ∫\frac{2}{(x+2)^2(2−x)}\,dx\)

32)\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx\) (Kidokezo: Tumia theorem ya mizizi ya busara.)

Jibu

\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx \quad = \quad \ln|x−2|−\tfrac{1}{2}\ln|x^2+2x+2|+C\)

Katika mazoezi ya 33 - 46, tumia badala ya kubadili integrals kwa integrals ya kazi za busara. Kisha utumie sehemu ndogo ili kutathmini integrals.

33)\(\displaystyle ∫^1_0\frac{e^x}{36−e^{2x}}\,dx\) (Kutoa jibu halisi na sawa na decimal. Pande zote hadi sehemu tano za decimal.)

34)\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx\)

Jibu

\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx \quad = \quad −x+\ln|1−e^x|+C\)

35)\(\displaystyle ∫\frac{\sin x\,dx}{1−\cos^2x}\)

36)\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx\)

Jibu

\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx \quad = \quad \tfrac{1}{5}\ln\left|\frac{\cos x+3}{\cos x−2}\right|+C\)

37)\(\displaystyle ∫\frac{1−\sqrt{x}}{1+\sqrt{x}}\,dx\)

38)\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2}\)

Jibu

\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2} \quad = \quad \frac{1}{2−2e^{2t}}+C\)

39)\(\displaystyle ∫\frac{1+e^x}{1−e^x}\,dx\)

40)\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}}\)

Jibu

\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}} \quad = \quad 2\sqrt{1+x}−2\ln|1+\sqrt{1+x}|+C\)

41)\(\displaystyle ∫\frac{dx}{\sqrt{x}+\sqrt[4]{x}}\)

42)\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx\)

Jibu

\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx \quad = \quad \ln\left|\frac{\sin x}{1−\sin x}\right|+C\)

43)\(\displaystyle ∫\frac{e^x}{(e^{2x}−4)^2}\,dx\)

44)\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx\)

Jibu

\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx \quad = \quad \frac{\sqrt{3}}{4}\)

45)\(\displaystyle ∫\frac{1}{2+e^{−x}}\,dx\)

46)\(\displaystyle ∫\frac{1}{1+e^x}\,dx\)

Jibu

\(\displaystyle ∫\frac{1}{1+e^x}\,dx \quad = \quad x−\ln(1+e^x)+C\)

Katika mazoezi 47 - 48, tumia nafasi iliyotolewa ili kubadilisha muhimu kwa kazi muhimu ya kazi ya busara, kisha tathmini.

47)\(\displaystyle ∫\frac{1}{t−\sqrt[3]{t}}\,dt; \quad t=x^3\)

48)\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx; \quad x=u^6\)

Jibu

\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx \quad = \quad 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln(1+x^{1/6})+C\)

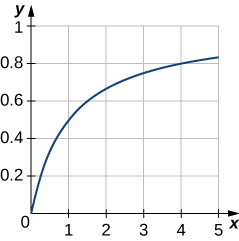
49) Graph curve\(y=\dfrac{x}{1+x}\) juu ya muda\([0,5]\). Kisha, tafuta eneo la kanda lililofungwa na pembe,\(x\) -axis, na mstari\(x=4\).

50) Kupata kiasi cha imara yanayotokana wakati mkoa imepakana\(y=\dfrac{1}{\sqrt{x(3−x)}}, \,y=0, \,x=1,\) na\(x=2\) ni revolved kuhusu\(x\) -axis.

Jibu

\(V = \frac{4}{3}π\text{arctanh}\,\left[\frac{1}{3}\right]=\frac{1}{3}π\ln 4 \, \text{units}^3\)

51) Kasi ya chembe inayohamia kando ya mstari ni kazi ya muda iliyotolewa na\(v(t)=\dfrac{88t^2}{t^2+1}.\) Tafuta umbali ambao chembe imesafiri baada ya\(t=5\) sekunde.

Katika mazoezi 52 - 54, tatua tatizo la thamani ya awali kwa\(x\) kama kazi ya\(t\).

52)\((t^2−7t+12)\dfrac{dx}{dt}=1,\quad t>4,\, x(5)=0\)

Jibu

\( x=−\ln|t−3|+\ln|t−4|+\ln 2 = \ln\left| \dfrac{2(t-4)}{t-3}\right|\)

53)\((t+5)\dfrac{dx}{dt}=x^2+1, \quad t>−5,\,x(1)=\tan 1\)

54)\((2t^3−2t^2+t−1)\dfrac{dx}{dt}=3,\quad x(2)=0\)

Jibu

\(x=\ln|t−1|−\sqrt{2}\arctan(\sqrt{2}t)−\frac{1}{2}\ln(t^2+\frac{1}{2})+\sqrt{2}\arctan(2\sqrt{2})+\frac{1}{2}\ln 4.5\)

55) Pata\(x\) -kuratibu ya centroid ya eneo lililofungwa\(y(x^2−9)=1, \, y=0, \,x=4,\) na\(x=5.\) (Pindua jibu kwa maeneo mawili ya decimal.)

56) Pata kiasi kilichozalishwa na kuzunguka eneo lililofungwa na\(y=\dfrac{1}{x^3+7x^2+6x},\, x=1,\, x=7\), na\(y=0\) kuhusu\(y\) -axis.

Jibu

\(V = \frac{2}{5}π\ln\frac{28}{13} \, \text{units}^3\)

57) Pata eneo lililofungwa\(y=\dfrac{x−12}{x^2−8x−20}, \,y=0, \,x=2,\) na\(x=4\). (Pindua jibu kwa karibu mia moja.)

58) Tathmini muhimu\(\displaystyle ∫\frac{dx}{x^3+1}.\)

Jibu

\(\displaystyle ∫\frac{dx}{x^3+1} \quad = \quad \frac{\arctan[\frac{−1+2x}{\sqrt{3}}]}{\sqrt{3}}+\frac{1}{3}\ln|1+x|−\frac{1}{6}\ln∣1−x+x^2∣+C\)

Kwa matatizo 59 - 62, tumia mbadala\(\tan(\frac{x}{2})=t, \,dx=\dfrac{2}{1+t^2}\,dt, \, \sin x=\dfrac{2t}{1+t^2},\) na\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

59)\(\displaystyle ∫\frac{dx}{3−5\sin x}\)

60) Kupata eneo chini ya Curve\(y=\dfrac{1}{1+\sin x}\) kati\(x=0\) na\(x=π.\) (Kudhani vipimo ni katika inchi.)

Jibu

2.0 ndani. ²

61) Kutokana\(\tan\left(\frac{x}{2}\right)=t,\) hupata formula\(dx=\dfrac{2}{1+t^2}dt, \,\sin x=\dfrac{2t}{1+t^2}\), na\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

62) Tathmini\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx.\)

Jibu

\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx \quad = \quad 3(−8+x)^{1/3}−2\sqrt{3}\arctan\left[\frac{−1+(−8+x)^{1/3}}{\sqrt{3}}\right]−2\ln\left[2+(−8+x)^{1/3}\right]+\ln\left[4−2(−8+x)^{1/3}+(−8+x)^{2/3}\right]+C\)