7.1: Ushirikiano na Sehemu

Malengo ya kujifunza

• Tambua wakati wa kutumia ushirikiano na sehemu.
• Tumia formula ya ushirikiano na-sehemu ili kutatua matatizo ya ushirikiano.
• Tumia formula ya ushirikiano na-sehemu kwa integrals uhakika.

Kwa sasa tuna utaratibu wa uhakika wa jinsi ya kutathmini integrals nyingi za msingi. Hata hivyo, ingawa tunaweza kuunganisha$∫x \sin (x^2)\,dx$ kwa kutumia badala$u=x^2$, kitu rahisi kuangalia kama$∫x\sin x\,\,dx$ anakataa sisi. Wanafunzi wengi wanataka kujua kama kuna utawala wa bidhaa kwa ushirikiano. Hakuna, lakini kuna mbinu inayotokana na utawala wa bidhaa kwa kutofautisha ambayo inaruhusu sisi kubadilishana moja muhimu kwa mwingine. Tunaita ushirikiano wa mbinu hii na sehemu.

Mfumo wa Ushirikiano na sehemu

Ikiwa$h(x)=f(x)g(x)$, basi kwa kutumia utawala wa bidhaa, tunapata

$$h′(x)=f′(x)g(x)+g′(x)f(x). \label{eq1}$$

Ingawa kwa mara ya kwanza inaweza kuonekana kuwa na matokeo mabaya, hebu sasa tuunganishe pande zote mbili za Equation\ ref {eq1}:

$$∫h′(x)\,\,dx=∫(g(x)f′(x)+f(x)g′(x))\,\,dx. \nonumber$$

Hii inatupa

$$h(x)=f(x)g(x)=∫g(x)f′(x)\,dx+∫f(x)g′(x)\,\,dx. \nonumber$$

Sasa sisi kutatua kwa$∫f(x)g′(x)\,\,dx:$

$$∫f(x)g′(x)\,dx=f(x)g(x)−∫g(x)f′(x)\,\,dx. \nonumber$$

Kwa kufanya mbadala$u=f(x)$ na$v=g(x)$, ambayo kwa upande hufanya,$du=f′(x)\,dx$ na$dv=g′(x)\,dx$, tuna fomu ya compact zaidi

$$∫u\,dv=uv−∫v\,du. \nonumber$$

Ushirikiano na Sehemu

Hebu$u=f(x)$ na$v=g(x)$ uwe kazi na derivatives zinazoendelea. Kisha, formula ya ushirikiano na-sehemu kwa muhimu inayohusisha kazi hizi mbili ni:

$$∫u\,dv=uv−∫v\,du. \label{IBP}$$

Faida ya kutumia formula ya ushirikiano na-sehemu ni kwamba tunaweza kuitumia ili kubadilishana moja muhimu kwa mwingine, labda rahisi, muhimu. Mfano unaofuata unaonyesha matumizi yake.

Mfano$\PageIndex{1}$: Using Integration by Parts

Tumia ushirikiano na sehemu$u=x$ na$dv=\sin x\,\,dx$ kutathmini

$$∫x\sin x\,\,dx. \nonumber$$

Suluhisho

Kwa kuchagua$u=x$, tuna$du=1\,\,dx$. Tangu$dv=\sin x\,\,dx$, tunapata

$$v=∫\sin x\,\,dx=−\cos x. \nonumber$$

Ni Handy kuweka wimbo wa maadili haya kama ifuatavyo:

• $u=x$
• $dv=\sin x\,\,dx$
• $du=1\,dx$
• $v=∫\sin x\,\,dx=−\cos x.$

Kutumia formula ya ushirikiano na-sehemu (Equation\ ref {IBP}) matokeo

$$\begin{align} ∫x\sin x\,\,dx &=(x)(−\cos x)−∫(−\cos x)(1\,\,dx) \tag{Substitute} \\[4pt] &=−x\cos x+∫\cos x\,\,dx \tag{Simplify} \end{align}$$

Kisha utumie

$$∫\cos x\,\,dx =\sin x+C. \nonumber$$

ili kupata

$$∫x\sin x\,\,dx =−x\cos x+\sin x+C. \nonumber$$

Uchambuzi

Kwa hatua hii, kuna pengine vitu vichache vinavyohitaji ufafanuzi. Kwanza kabisa, unaweza kuwa na hamu kuhusu nini kitatokea kama tungechagua$u=\sin x$ na$dv=x$. Ikiwa tulikuwa tumefanya hivyo, basi tungekuwa$du=\cos x$ na$v=\dfrac{1}{2}x^2$. Hivyo, baada ya kutumia ushirikiano na sehemu (Equation\ ref {IBP}), tuna

$$∫​x\sin x\,\,dx=\dfrac{1}{2}x^2\sin x−∫\dfrac{1}{2}x^2\cos x\,\,dx. \nonumber$$

Kwa bahati mbaya, pamoja na muhimu mpya, hatuko katika nafasi nzuri zaidi kuliko hapo awali. Ni muhimu kukumbuka kwamba tunapoomba ushirikiano na sehemu, tunaweza kuhitaji kujaribu uchaguzi kadhaa$u$ na$dv$ kabla ya kupata uchaguzi unaofanya kazi.

Pili, unaweza kushangaa kwa nini$v=∫​\sin x\,\,dx=−\cos x$, wakati sisi kupata, hatutumii$v=−\cos x+K.$ Ili kuona kwamba haina tofauti, tunaweza rework tatizo kwa kutumia$v=−\cos x+K$:

$$\begin{align*} ∫x\sin x\,\,dx &=(x)(−\cos x+K)−∫(−\cos x+K)(1\,\,dx) \\[4pt] &=−x\cos x+Kx+∫\cos x\,\,dx−∫K\,\,dx \\[4pt] &=−x\cos x+Kx+\sin x−Kx+C \\[4pt] &=−x\cos x+\sin x+C. \end{align*}$$

Kama unaweza kuona, haina tofauti katika suluhisho la mwisho.

Mwisho, tunaweza kuangalia ili kuhakikisha kwamba antiderivative yetu ni sahihi kwa kutofautisha$−x\cos x+\sin x+C:$

$$\begin{align*} \dfrac{d}{\,dx}(−x\cos x+\sin x+C) = \cancel{(−1)\cos x} + (−x)(−\sin x) + \cancel{\cos x} \\[4pt] =x\sin x \end{align*}$$

Kwa hiyo, antiderivative hundi nje.

Zoezi$\PageIndex{1}$

Tathmini$∫​xe^{2x}\,dx$ kutumia formula ya ushirikiano na-sehemu (Equation\ ref {IBP}) na$u=x$ na$dv=e^{2x}\,\,dx$.

Kidokezo

Kupata$du$ na$v$, na kutumia mfano uliopita kama mwongozo.

Jibu

$$∫​xe^{2x}\,\,dx=\dfrac{1}{2}xe^{2x}−\dfrac{1}{4}e^{2x}+C \nonumber$$

Swali la asili la kuuliza kwa hatua hii ni: Tunajuaje jinsi ya kuchagua$u$ na$dv$? Wakati mwingine ni suala la jaribio na hitilafu; hata hivyo, kifupi LIATE kinaweza kusaidia kuchukua baadhi ya guesswork nje ya uchaguzi wetu. Kifupi hiki kinasimama kwa Kazi za L ogarithmic, Kazi za Trigonometric, Kazi za Legebraic, Kazi za Rigonometric, na Kazi za ufanisi za E. Mnemonic hii hutumika kama msaada katika kuamua uchaguzi sahihi kwa$u$. Aina ya kazi katika muhimu ambayo inaonekana kwanza katika orodha inapaswa kuwa uchaguzi wetu wa kwanza wa$u$.

Kwa mfano, ikiwa muhimu ina kazi ya logarithmic na kazi ya algebraic, tunapaswa$u$ kuchagua kuwa kazi ya logarithmic, kwa sababu L huja kabla ya A katika LIATE. Muhimu katika Mfano$\PageIndex{1}$ ina kazi ya trigonometric ($\sin x$) na kazi ya algebraic ($x$). Kwa sababu A huja kabla ya T katika LIATE, tulichagua$u$ kuwa kazi ya algebraic. Wakati sisi wamechagua$u$,$dv$ ni kuchaguliwa kuwa sehemu iliyobaki ya kazi ya kuwa jumuishi, pamoja na$\,dx$.

Kwa nini kazi hii ya mnemonic? Kumbuka kwamba chochote sisi kuchukua kuwa$dv$ lazima kitu tunaweza kuunganisha. Kwa kuwa hatuna formula za ushirikiano ambazo zinatuwezesha kuunganisha kazi rahisi za logarithmic na kazi za trigonometric inverse, ni busara kwamba haipaswi kuchaguliwa kama maadili$dv$. Kwa hiyo, wanapaswa kuwa katika kichwa cha orodha kama uchaguzi$u$. Hivyo, tunaweka LI mwanzoni mwa mnemonic. (Tunaweza tu kwa urahisi wameanza na IL, tangu aina hizi mbili za kazi si kuonekana pamoja katika tatizo ushirikiano na-sehemu.) Kazi ya kielelezo na trigonometric ni mwisho wa orodha yetu kwa sababu ni rahisi kuunganisha na kufanya uchaguzi mzuri kwa$dv$. Hivyo, tuna TE mwishoni mwa mnemonic yetu. (Tunaweza tu kama urahisi wametumia ET mwishoni, tangu wakati aina hizi za kazi kuonekana pamoja kwa kawaida haina kweli jambo ambalo ni moja$u$ na ambayo ni moja$dv$.) Kazi za algebraic kwa ujumla ni rahisi kuunganisha na kutofautisha, na huja katikati ya mnemonic.

Mfano$\PageIndex{2}$: Using Integration by Parts

Tathmini $$∫\dfrac{\ln x}{x^3}\,\,dx. \nonumber$$

Suluhisho

Anza kwa kuandika upya muhimu:

$$∫\dfrac{\ln x}{x^3}\,\,dx=∫​x^{−3}\ln x\,\,dx. \nonumber$$

Kwa kuwa muhimu hii ina kazi ya algebraic$x^{−3}$ na kazi ya logarithmic$\ln x$, chagua$u=\ln x$, tangu$L$ inakuja kabla A katika LIATE. Baada ya kuchaguliwa$u=\ln x$, lazima tuchague$dv=x^{−3}\,dx$.

Next, tangu$u=\ln x,$ tuna$du=\dfrac{1}{x}\,dx.$ Pia,$v=∫​x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.$ muhtasari,

• $u=\ln x$
• $du=\dfrac{1}{x}\,dx$
• $dv=x^{−3}\,dx$
• $v=∫​x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.$

Kubadilisha katika formula ya ushirikiano na-sehemu (Equation\ ref {IBP}) inatoa

$$\begin{align*} ∫\dfrac{\ln x}{x^3}\,dx &=∫​x^{−3}\ln x\,dx=(\ln x)(−\dfrac{1}{2}x^{−2})−∫​(−\dfrac{1}{2}x^{−2})(\dfrac{1}{x}\,dx) \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x+∫\dfrac{1}{2}x^{−3}\,\,dx \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x−\dfrac{1}{4}x^{−2}+C\ \\[4pt] &=−\dfrac{1}{2x^2}\ln x−\dfrac{1}{4x^2}+C \end{align*} \nonumber$$

Zoezi$\PageIndex{2}$

Tathmini $$∫​x\ln x \,\,dx. \nonumber$$

Kidokezo

Tumia$u=\ln x$ na$dv=x\,\,dx$.

Jibu

$$∫​x\ln x \,\,dx=\dfrac{1}{2}x^2\ln x−\dfrac{1}{4}x^2+C \nonumber$$

Katika hali nyingine, kama katika mifano miwili ijayo, inaweza kuwa muhimu kuomba ushirikiano na sehemu zaidi ya mara moja.

Mfano$\PageIndex{3A}$: Applying Integration by Parts More Than Once

Tathmini $$∫​x^2e^{3x}\,dx. \nonumber$$

Suluhisho

Kutumia LIATE, chagua$u=x^2$ na$dv=e^{3x}\,dx$. Hivyo,$du=2x\,dx$ na$v=∫e^{3x}\,dx=\left(\dfrac{1}{3}\right)e^{3x}$. Kwa hiyo,

• $u=x^2$
• $du=2x\,dx$
• $dv=e^{3x}\,dx$
• $v=∫e^{3x}\,dx=\dfrac{1}{3}e^{3x}.$

Kubadilisha katika Equation\ ref {IBP} inazalisha

$$∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−∫\dfrac{2}{3}xe^{3x}\,dx. \label{3A.2}$$

Bado hatuwezi kuunganisha$∫\dfrac{2}{3}xe^{3x}\,dx$ moja kwa moja, lakini muhimu sasa ina nguvu ya chini$x$. Tunaweza kutathmini hii muhimu mpya kwa kutumia ushirikiano na sehemu tena. Ili kufanya hivyo, chagua

$$u=x \nonumber$$

na

$$dv=\dfrac{2}{3}e^{3x}\,dx. \nonumber$$

Hivyo,

$$du=\,dx \nonumber$$

na

$$v=∫\left(\dfrac{2}{3}\right)e^{3x}\,dx=\left(\dfrac{2}{9}\right)e^{3x}. \nonumber$$

Sasa tuna

• $u=x$
• $du=\,dx$
• $dv=\dfrac{2}{3}e^{3x}\,dx$
• $\displaystyle v=∫\dfrac{2}{3}e^{3x}\,dx=\dfrac{2}{9}e^{3x}.$

Kubadilisha nyuma katika Equation\ ref {3A.2} mavuno

$$∫​x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\left(\dfrac{2}{9}xe^{3x}−∫\dfrac{​2}{9}e^{3x}\,dx\right). \nonumber$$

Baada ya kutathmini muhimu ya mwisho na kurahisisha, tunapata

$$∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\dfrac{2}{9}xe^{3x}+\dfrac{2}{27}e^{3x}+C. \nonumber$$

Mfano$\PageIndex{3B}$: Applying Integration by Parts When LIATE Does not Quite Work

Tathmini

$$∫​t^3e^{t^2}dt. \nonumber$$

Suluhisho

Ikiwa tunatumia tafsiri kali ya LIATE ya mnemonic ili kufanya uchaguzi wetu$u$, tunaishia$u=t^3$ na$dv=e^{t^2}dt$. Kwa bahati mbaya, uchaguzi huu si kazi kwa sababu hatuwezi kutathmini$∫​e^{t^2}dt$. Hata hivyo, tangu tunaweza kutathmini$∫​te^{t^2}\,dx$, tunaweza kujaribu kuchagua$u=t^2$$dv=te^{t^2}dt.$ na Kwa uchaguzi huu tuna

• $u=t^2$
• $du=2tdt$
• $dv=te^{t^2}dt$
• $v=∫​te^{t^2}dt=\dfrac{1}{2}e^{t^2}.$

Hivyo, sisi kupata

$$\begin{align*} ∫t^3e^{t^2}dt =\dfrac{1}{2}t^2e^{t^2}−∫\dfrac{1}{2}e^{t^2}2t\,dt \\[4pt] =\dfrac{1}{2}t^2e^{t^2}−\dfrac{1}{2}e^{t^2}+C. \end{align*}$$

Mfano$\PageIndex{3C}$: Applying Integration by Parts More Than Once

Tathmini $$∫​\sin (\ln x)\,dx. \nonumber$$

Suluhisho

Hii muhimu inaonekana kuwa moja tu kazi-yaani,$\sin (\ln x)$ -Hata hivyo, tunaweza daima kutumia kazi ya mara kwa mara 1 kama kazi nyingine. Katika mfano huu, hebu tuchague$u=\sin (\ln x)$ na$dv=1\,dx$. (Uamuzi wa kutumia$u=\sin (\ln x)$ ni rahisi. Hatuwezi kuchagua$dv=\sin (\ln x)\,dx$ kwa sababu kama tungeweza kuunganisha, hatutatumia ushirikiano kwa sehemu katika nafasi ya kwanza!) Kwa hiyo,$du=(1/x)\cos (\ln x) \,dx$ na$v=∫​ 1 \,dx=x.$ Baada ya kutumia ushirikiano na sehemu muhimu na kurahisisha, tuna

$$∫​\sin \left(\ln x\right) \,dx=x \sin (\ln x)−\int \cos (\ln x)\,dx. \nonumber$$

Kwa bahati mbaya, mchakato huu unatuacha na muhimu mpya ambayo ni sawa na ya awali. Hata hivyo, hebu angalia nini kinatokea wakati sisi kuomba ushirikiano na sehemu tena. Wakati huu hebu tuchague$u=\cos (\ln x)$ na$dv=1\,dx,$ kufanya$du=−(1/x)\sin (\ln x)\,dx$ na$v=∫​1\,dx=x.$

Kubadilisha, tuna

$$∫​\sin (\ln x)\,dx=x \sin (\ln x)−(x \cos (\ln x)-∫​−\sin (\ln x)\,dx). \nonumber$$

Baada ya kurahisisha, tunapata

$$∫​\sin (\ln x)\,dx=x\sin (\ln x)−x \cos (\ln x)−∫​\sin (\ln x)\,dx. \nonumber$$

Muhimu wa mwisho sasa ni sawa na ya awali. Inaweza kuonekana kwamba tumekwenda kwenye mduara, lakini sasa tunaweza kweli kutathmini muhimu. Kuona jinsi ya kufanya hivyo kwa uwazi zaidi, mbadala$I=∫​\sin (\ln x)\,dx.$ Hivyo, equation inakuwa

$$I=x \sin (\ln x)−x \cos (\ln x)−I. \nonumber$$

Kwanza,$I$ kuongeza pande zote mbili za equation kupata

$$2I=x \sin (\ln x)−x \cos (\ln x). \nonumber$$

Kisha, ugawanye na 2:

$$I=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber$$

Kubadilisha$I=∫​\sin (\ln x)\,dx$ tena, tuna

$$\int \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber$$

Kutokana na hili tunaona kwamba$(1/2)x \sin (\ln x)−(1/2)x \cos (\ln x)$ ni antiderivative ya$\sin (\ln x)\,dx$. Kwa antiderivative ya jumla, ongeza$+C$:

$$∫ \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x)+C. \nonumber$$

Uchambuzi

Ikiwa njia hii inahisi ajabu kidogo kwa mara ya kwanza, tunaweza kuangalia jibu kwa kutofautisha:

$$\begin{align*} \dfrac{d}{\,dx}\left(\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x\cos (\ln x)\right) \\[4pt] &=\dfrac{1}{2}(\sin (\ln x))+\cos (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x−\left(\dfrac{1}{2}\cos (\ln x)−\sin (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x\right) \\[4pt] &=\sin (\ln x). \end{align*}$$

Zoezi$\PageIndex{3}$

Tathmini $$∫x^2\sin x\,dx. \nonumber$$

Kidokezo

Hii ni sawa na Mifano$\PageIndex{3A}$ -$\PageIndex{3C}$.

Jibu

$$∫x^2\sin x\,dx=−x^2\cos x+2x\sin x+2\cos x+C \nonumber$$

Ushirikiano na Parts kwa Integrals uhakika

Sasa kwa kuwa tumetumia ushirikiano na sehemu kwa mafanikio kutathmini integrals usio na kipimo, tunageuka mawazo yetu kwa integrals ya uhakika. Mbinu ya ushirikiano ni sawa, tu tunaongeza hatua ya kutathmini muhimu katika mipaka ya juu na ya chini ya ushirikiano.

Ushirikiano na Parts kwa Integrals uhakika

Hebu$u=f(x)$ na$v=g(x)$ uwe kazi na derivatives zinazoendelea kwenye [$a,b$]. Kisha

$$∫^b_a u\,dv=uv\Big|^b_a−∫^b_a v\, du \nonumber$$

Mfano$\PageIndex{4A}$: Finding the Area of a Region

Pata eneo la kanda lililofungwa hapo juu na grafu ya$y=\tan^{−1}x$ na chini na$x$ -axis juu ya muda [$0,1$].

Suluhisho

Mkoa huu umeonyeshwa kwenye Kielelezo$\PageIndex{1}$. Ili kupata eneo hilo, ni lazima tathmini

$$∫^1_0 \tan^{−1}x\, \,dx. \nonumber$$

Kielelezo$\PageIndex{1}$: Ili kupata eneo la kanda la kivuli, tunapaswa kutumia ushirikiano na sehemu.

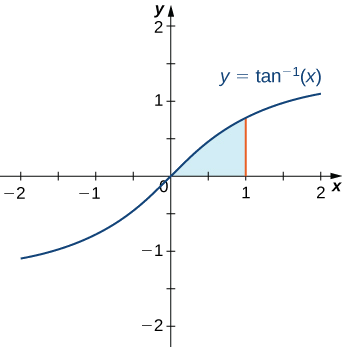
Kwa hili muhimu, hebu tuchague$u=tan^{−1}x$ na$dv=\,dx$, na hivyo$du=\dfrac{1}{x^2+1}\,dx$ tufanye na$v=x$. Baada ya kutumia formula ya ushirikiano na-sehemu (Equation\ ref {IBP}) tunapata

$$\text{Area}=\left. x \tan^{−1} x \right|^1_0−∫^1_0 \dfrac{x}{x^2+1} \,dx. \nonumber$$

Matumizi$u$ -badala ya kupata

$$∫^1_0\dfrac{x}{x^2+1}\,dx=\left.\dfrac{1}{2}\ln \left(x^2+1\right) \right|^1_0. \nonumber$$

Hivyo,

$$\text{Area}=x \tan^{−1}x \Big|^1_0− \left.\dfrac{1}{2}\ln \left( x^2+1 \right) \right|^1_0=\left(\dfrac{π}{4}−\dfrac{1}{2}\ln 2\right) \,\text{units}^2. \nonumber$$

Katika hatua hii inaweza kuwa wazo mbaya kufanya “kuangalia ukweli” juu ya reasonableness ya ufumbuzi wetu. Tangu$\dfrac{π}{4}−\dfrac{1}{2}\ln 2≈0.4388\,\text{units}^2,$ na kutoka Kielelezo$\PageIndex{1}$ tunatarajia eneo letu kuwa kidogo chini ya ufumbuzi$0.5\,\text{units}^2,$ huu inaonekana kuwa busara.

Mfano$\PageIndex{4B}$: Finding a Volume of Revolution

Pata kiasi cha imara iliyopatikana kwa kuzunguka eneo lililofungwa na grafu$f(x)=e^{−x},$ ya$x$ -axis,$y$ -axis, na mstari$x=1$ kuhusu$y$ -axis.

Suluhisho

Chaguo bora ya kutatua tatizo hili ni kutumia njia ya shell. Anza kwa sketching kanda kuwa revolved, pamoja na mstatili kawaida (Kielelezo$\PageIndex{2}$).

Kielelezo$\PageIndex{2}$: Tunaweza kutumia njia ya shell ili kupata kiasi cha mapinduzi.

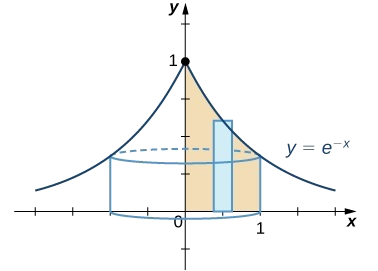
Ili kupata kiasi kwa kutumia shells, lazima tathmini

$$2π∫^1_0xe^{−x}\,dx. \label{4B.1}$$

Ili kufanya hivyo, basi$u=x$ na$dv=e^{−x}$. Uchaguzi huu unasababisha$du=\,dx$ na$v=∫​e^{−x}\,dx=−e^{−x}.$ Kutumia formula ya Njia ya Shell, tunapata

\ [kuanza {align*}\ Nakala {Volume} &=2π^1_0xe^ {-x}\, dx\\ [4pt] = 2π\ kushoto (-xe^ {-x}\ Big|^1_0+^1_0E^ {-x}\\, dx\ haki)\ tag {Tumia ushirikiano na sehemu}\\ [4pt]
&= 2_0E^ {-x}\ π\ kushoto (-e^ {-1} + 0 - e^ {-x}\ Big|^1_0\ haki)\\ [4pt]
&= 2π\ kushoto (-e^ {-1} - e^ {-1} + 1\ haki)\\ [4pt]
&= 2π\ kushoto (1 -\ dfrac {2} {e}\ haki)\,\ maandishi {vitengo} ^3. \ tag {Tathmini na kurahisisha}\ mwisho {align*}\]

Uchambuzi

Tena, ni wazo nzuri ya kuangalia reasonableness ya ufumbuzi wetu. Tunaona kwamba imara ina kiasi kidogo kidogo kuliko ile ya silinda ya radius$1$ na urefu wa$1/e$ aliongeza kwa kiasi cha koni ya msingi radius$1$ na urefu wa$1−\dfrac{1}{e}.$ Kwa hiyo, imara inapaswa kuwa na kiasi kidogo chini ya

$$π(1)^2\dfrac{1}{e}+\left(\dfrac{π}{3}\right)(1)^2\left(1−\dfrac{1}{e}\right)=\dfrac{2π}{3e}+\dfrac{π}{3}≈1.8177\,\text{units}^3. \nonumber$$

Kwa kuwa$2π−\dfrac{4π}{e}≈1.6603,$ tunaona kwamba kiasi chetu cha mahesabu ni busara.

Zoezi$\PageIndex{4}$

Tathmini $$∫^{π/2}_0x\cos x\,dx. \nonumber$$

Kidokezo

Matumizi Equation\ ref {IBP}$u=x$ na$dv=\cos x\,dx.$

Jibu

$$∫^{π/2}_0x\cos x\,dx = \dfrac{π}{2}−1 \nonumber$$

Dhana muhimu

• Fomu ya ushirikiano na-sehemu (Equation\ ref {IBP}) inaruhusu kubadilishana moja muhimu kwa mwingine, labda rahisi, muhimu.
• Ushirikiano na sehemu inatumika kwa integrals wote uhakika na usio na kipimo.

Mlinganyo muhimu

• Ushirikiano na sehemu formula

$\displaystyle ∫u\,dv=uv−∫v\,du$

• Ushirikiano na sehemu kwa integrals uhakika

$\displaystyle ∫^b_au\,dv=uv\Big|^b_a−∫^b_av\,du$

faharasa

ushirikiano na sehemu

mbinu ya ushirikiano ambayo inaruhusu kubadilishana moja muhimu kwa mwingine kwa kutumia formula$\displaystyle ∫​u\,dv=uv−∫​v\,du$