7.1E: Mazoezi ya Sehemu ya 7.1

Last updated
Save as PDF

Page ID: 178861

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Kwa kutumia mbinu ya ushirikiano na sehemu, lazima uangalie kwa makini maneno gani\(u\). Kwa kila moja ya matatizo yafuatayo, tumia miongozo katika sehemu hii ya kuchagua\(u\). Je, si kutathmini integrals.

1)\(\displaystyle ∫x^3e^{2x}\,dx\)

Jibu: \( u=x^3\)

2)\(\displaystyle ∫x^3\ln(x)\,dx\)

3)\(\displaystyle ∫y^3\cos y\,dy\)

Jibu: \(u=y^3\)

4)\(\displaystyle ∫x^2\arctan x\,dx\)

5)\(\displaystyle ∫e^{3x}\sin(2x)\,dx\)

Jibu: \(u=\sin(2x)\)

Katika mazoezi ya 6 - 37, tafuta muhimu kwa kutumia njia rahisi. Si matatizo yote yanahitaji ushirikiano na sehemu.

6)\(\displaystyle ∫v\sin v\,dv\)

7)\(\displaystyle ∫\ln x\,dx\) (Kidokezo:\(\displaystyle ∫\ln x\,dx\) ni sawa na\(\displaystyle ∫1⋅\ln(x)\,dx.)\)

Jibu: \(\displaystyle ∫\ln x\,dx \quad = \quad−x+x\ln x+C\)

8)\(\displaystyle ∫x\cos x\,dx\)

9)\(\displaystyle ∫\tan^{−1}x\,dx\)

Jibu: \(\displaystyle ∫\tan^{−1}x\,dx\quad = \quad x\tan^{−1}x−\tfrac{1}{2}\ln(1+x^2)+C\)

10)\(\displaystyle ∫x^2e^x\,dx\)

11)\(\displaystyle ∫x\sin(2x)\,dx\)

Jibu: \(\displaystyle ∫x\sin(2x)\,dx \quad = \quad −\tfrac{1}{2}x\cos(2x)+\tfrac{1}{4}\sin(2x)+C\)

12)\(\displaystyle ∫xe^{4x}\,dx\)

13)\(\displaystyle ∫xe^{−x}\,dx\)

Jibu: \(\displaystyle ∫xe^{−x}\,dx \quad = \quad e^{−x}(−1−x)+C\)

14)\(\displaystyle ∫x\cos 3x\,dx\)

15)\(\displaystyle ∫x^2\cos x\,dx\)

Jibu: \(\displaystyle ∫x^2\cos x\,dx \quad = \quad 2x\cos x+(−2+x^2)\sin x+C\)

16)\(\displaystyle ∫x\ln x\,dx\)

17)\(\displaystyle ∫\ln(2x+1)\,dx\)

Jibu: \(\displaystyle ∫\ln(2x+1)\,dx \quad = \quad \tfrac{1}{2}(1+2x)(−1+\ln(1+2x))+C\)

18)\(\displaystyle ∫x^2e^{4x}\,dx\)

19)\(\displaystyle ∫e^x\sin x\,dx\)

Jibu: \(\displaystyle ∫e^x\sin x\,dx \quad = \quad \tfrac{1}{2}e^x(−\cos x+\sin x)+C\)

20)\(\displaystyle ∫e^x\cos x\,dx\)

21)\(\displaystyle ∫xe^{−x^2}\,dx\)

Jibu: \(\displaystyle ∫xe^{−x^2}\,dx \quad = \quad −\frac{e^{−x^2}}{2}+C\)

22)\(\displaystyle ∫x^2e^{−x}\,dx\)

23)\(\displaystyle ∫\sin(\ln(2x))\,dx\)

Jibu: \(\displaystyle ∫\sin(\ln(2x))\,dx \quad = \quad −\tfrac{1}{2}x\cos[\ln(2x)]+\tfrac{1}{2}x\sin[\ln(2x)]+C\)

24)\(\displaystyle ∫\cos(\ln x)\,dx\)

25)\(\displaystyle ∫(\ln x)^2\,dx\)

Jibu: \(\displaystyle ∫(\ln x)^2\,dx \quad = \quad 2x−2x\ln x+x(\ln x)^2+C\)

26)\(\displaystyle ∫\ln(x^2)\,dx\)

27)\(\displaystyle ∫x^2\ln x\,dx\)

Jibu: \(\displaystyle ∫x^2\ln x\,dx \quad = \quad −\frac{x^3}{9}+\tfrac{1}{3}x^3\ln x+C\)

28)\(\displaystyle ∫\sin^{−1}x\,dx\)

29)\(\displaystyle ∫\cos^{−1}(2x)\,dx\)

Jibu: \(\displaystyle ∫\cos^{−1}(2x)\,dx \quad = \quad −\tfrac{1}{2}\sqrt{1−4x^2}+x\cos^{−1}(2x)+C\)

30)\(\displaystyle ∫x\arctan x\,dx\)

31)\(\displaystyle ∫x^2\sin x\,dx\)

Jibu: \(\displaystyle ∫x^2\sin x\,dx \quad = \quad −(−2+x^2)\cos x+2x\sin x+C\)

32)\(\displaystyle ∫x^3\cos x\,dx\)

33)\(\displaystyle ∫x^3\sin x\,dx\)

Jibu: \(\displaystyle ∫x^3\sin x\,dx \quad = \quad −x(−6+x^2)\cos x+3(−2+x^2)\sin x+C\)

34)\(\displaystyle ∫x^3e^x\,dx\)

35)\(\displaystyle ∫x\sec^{−1}x\,dx\)

Jibu: \(\displaystyle ∫x\sec^{−1}x\,dx \quad = \quad \tfrac{1}{2}x\left(−\sqrt{1−\frac{1}{x^2}}+x⋅\sec^{−1}x\right)+C\)

36)\(\displaystyle ∫x\sec^2x\,dx\)

37)\(\displaystyle ∫x\cosh x\,dx\)

Jibu: \(\displaystyle ∫x\cosh x\,dx \quad = \quad −\cosh x+x\sinh x+C\)

Katika mazoezi 38 - 46, compute integrals uhakika. Tumia matumizi ya graphing ili kuthibitisha majibu yako.

38)\(\displaystyle ∫^1_{1/e}\ln x\,dx\)

39)\(\displaystyle ∫^1_0xe^{−2x}\,dx\) (Eleza jibu kwa fomu halisi.)

Jibu: \(\displaystyle ∫^1_0xe^{−2x}\,dx \quad = \quad \frac{1}{4}−\frac{3}{4e^2}\)

40)\(\displaystyle ∫^1_0e^{\sqrt{x}}\,dx \quad (\text{let}\, u=\sqrt{x})\)

41)\(\displaystyle ∫^e_1\ln(x^2)\,dx\)

Jibu: \(\displaystyle ∫^e_1\ln(x^2)\,dx \quad = \quad 2\)

42)\(\displaystyle ∫^π_0x\cos x\,dx\)

43)\(\displaystyle ∫^π_{−π}x\sin x\,dx\) (Eleza jibu kwa fomu halisi.)

Jibu: \(\displaystyle ∫^π_{−π}x\sin x\,dx \quad = \quad 2\pi\)

44)\(\displaystyle ∫^3_0\ln(x^2+1)\,dx\) (Eleza jibu kwa fomu halisi.)

45)\(\displaystyle ∫^{π/2}_0x^2\sin x\,dx\) (Eleza jibu kwa fomu halisi.)

Jibu: \(\displaystyle ∫^{π/2}_0x^2\sin x\,dx \quad = \quad −2+π\)

46)\(\displaystyle ∫^1_0x5^x\,dx\) (Eleza jibu kwa kutumia tarakimu tano muhimu.)

47) Tathmini\(\displaystyle ∫\cos x\ln(\sin x)\,dx\)

Jibu: \(\displaystyle ∫\cos x\ln(\sin x)\,dx \quad = \quad −\sin(x)+\ln[\sin(x)]\sin x+C\)

Katika mazoezi 48 - 50, hupata formula zifuatazo kwa kutumia mbinu ya ushirikiano na sehemu. Kudhani kwamba\(n\) ni integer chanya. Fomula hizi huitwa kupunguza formula kwa sababu exponent katika\(x\) muda imepungua kwa moja katika kila kesi. Muhimu wa pili ni rahisi kuliko muhimu ya awali.

48)\(\displaystyle ∫x^ne^x\,dx=x^ne^x−n∫x^{n−1}e^x\,dx\)

49)\(\displaystyle ∫x^n\cos x\,dx=x^n\sin x−n∫x^{n−1}\sin x\,dx\)

Jibu: Majibu hutofautiana

50)\(\displaystyle ∫x^n\sin x\,dx=\) ______

51) Unganisha\(\displaystyle ∫2x\sqrt{2x−3}\,dx\) kutumia njia mbili:

a Kutumia sehemu, kuruhusu\(dv=\sqrt{2x−3}\,dx\)

b Kubadilisha, kuruhusu\(u=2x−3\)

Jibu: a.\(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)
b.\(\displaystyle ∫2x\sqrt{2x−3}\,dx \quad = \quad \tfrac{2}{5}(1+x)(−3+2x)^{3/2}+C\)

Katika mazoezi 52 - 57, hali kama ungependa kutumia ushirikiano na sehemu ya kutathmini muhimu. Ikiwa ndivyo, tambua\(u\) na\(dv\). Kama siyo, kuelezea mbinu kutumika kufanya ushirikiano bila kweli kufanya tatizo.

52)\(\displaystyle ∫x\ln x\,dx\)

53)\(\displaystyle ∫\frac{\ln^2x}{x}\,dx\)

Jibu: Usitumie ushirikiano na sehemu. \(u\)Chagua kuwa\(\ln x\), na muhimu ni ya fomu\(\displaystyle ∫u^2\,du.\)

54)\(\displaystyle ∫xe^x\,dx\)

55)\(\displaystyle ∫xe^{x^2−3}\,dx\)

Jibu: Usitumie ushirikiano na sehemu. Hebu\(u=x^2−3\), na muhimu inaweza kuweka katika fomu\(∫e^u\,du\).

56)\(\displaystyle ∫x^2\sin x\,dx\)

57)\(\displaystyle ∫x^2\sin(3x^3+2)\,dx\)

Jibu: Usitumie ushirikiano na sehemu. \(u\)Chagua kuwa\(u=3x^3+2\) na muhimu inaweza kuweka katika fomu\(\displaystyle ∫\sin(u)\,du.\)

Katika mazoezi 58-59, mchoro eneo lililofungwa hapo juu na pembe,\(x\) -axis\(x=1\), na, na kupata eneo la kanda. Kutoa fomu halisi au majibu ya pande zote kwa idadi ya maeneo yaliyoonyeshwa.

58)\(y=2xe^{−x}\) (Jibu takriban kwa maeneo manne ya decimal.)

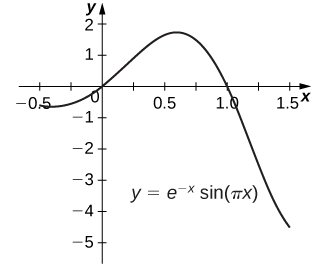
59)\(y=e^{−x}\sin(πx)\) (Jibu takriban kwa maeneo tano ya decimal.)

Jibu: Eneo chini ya grafu ni\(0.39535 \, \text{units}^2.\)

Katika mazoezi 60 - 61, pata kiasi kilichozalishwa na kupokezana eneo lililofungwa na curves zilizopewa kuhusu mstari maalum. Eleza majibu kwa fomu halisi au takriban idadi ya maeneo ya decimal yaliyoonyeshwa.

60)\(y=\sin x,\,y=0,\,x=2π,\,x=3π;\) kuhusu\(y\) -axis (Eleza jibu kwa fomu halisi.)

61)\(y=e^{−x}, \,y=0,\,x=−1, \, x=0;\) kuhusu\(x=1\) (Eleza jibu kwa fomu halisi.)

Jibu: \(V = 2πe \, \text{units}^3\)

62) Chembe inayohamia kwenye mstari wa moja kwa moja ina kasi ya\(v(t)=t^2e^{−t}\) baada ya\(t\) sekunde. Je, ni mbali gani kusafiri katika sekunde ya kwanza ya 2? (Kudhani vitengo ni katika miguu na kutoa jibu katika fomu halisi.)

63) Pata eneo chini ya grafu ya\(y=\sec^3x\) kutoka\(x=0\) kwa\(x=1\). (Pindua jibu kwa tarakimu mbili muhimu.)

Jibu: \(A= 2.05 \, \text{units}^2\)

64) Pata eneo kati\(y=(x−2)e^x\) na\(x\) -axis kutoka\(x=2\) kwa\(x=5\). (Eleza jibu kwa fomu halisi.)

65) Kupata eneo la mkoa iliyoambatanishwa\(y=x\cos x\) na Curve na\(x\) -axis kwa\(\frac{11π}{2}≤x≤\frac{13π}{2}.\) (Express jibu katika fomu halisi.)

Jibu: \(A = 12π \, \text{units}^2\)

66) Pata kiasi cha imara kilichozalishwa na kuzunguka kanda iliyofungwa na pembe\(y=\ln x\),\(x\) -axis, na mstari wa wima\(x=e^2\) kuhusu\(x\) -axis. (Eleza jibu kwa fomu halisi.)

67) Pata kiasi cha imara kilichozalishwa na kuzunguka eneo lililofungwa na pembe\(y=4\cos x\) na \(x\)-axis,\(\frac{π}{2}≤x≤\frac{3π}{2},\) kuhusu\(x\) -axis. (Eleza jibu kwa fomu halisi.)

Jibu: \(V = 8π^2 \, \text{units}^3\)

68) Kupata kiasi cha imara yanayotokana na yanazunguka kanda katika roboduara ya kwanza\(y=e^x\) imepakana na\(x\) -axis, kutoka\(x=0\) kwa\(x=\ln(7)\), kuhusu\(y\) -axis. (Eleza jibu kwa fomu halisi.)

69) Je! Ni kiasi gani cha keki ya Bundt inayotokana na kupokezana\( y=\sin x\) karibu na\(y\) -axis kutoka\( x=0\) kwa\( x=π\)?

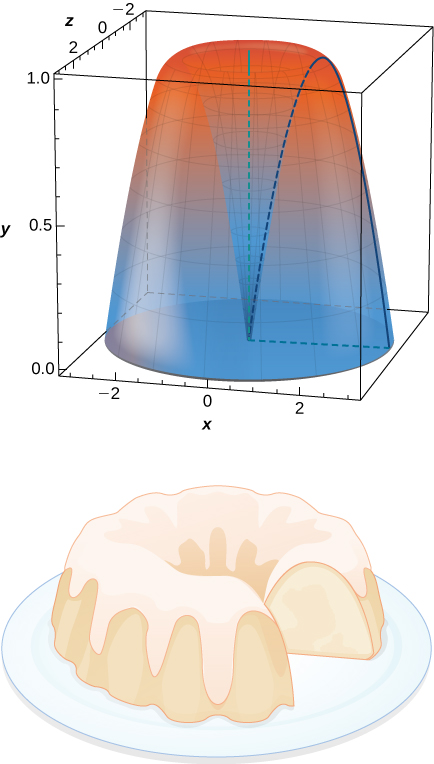
Jibu: \(V = 2π^2\)vitengo ³