Skip to main content
Global

6.6E: Mazoezi ya Sehemu ya 6.6

  1. Last updated
  2. Save as PDF
  • Page ID
    178409

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Katika mazoezi ya 1 - 6, hesabu katikati ya wingi kwa ajili ya ukusanyaji wa raia iliyotolewa.

    1)\(m_1=2\) saa\(x_1=1\) na\(m_2=4\) saa\(x_2=2\)

    2)\(m_1=1\) saa\(x_1=−1\) na\(m_2=3\) saa\(x_2=2\)

    Jibu
    \(x = \frac{5}{4}\)

    3)\(m=3\) katika\(x=0,1,2,6\)

    4) Kitengo cha raia\((x,y)=(1,0),(0,1),(1,1)\)

    Jibu
    \(\left(\frac{2}{3},\, \frac{2}{3}\right)\)

    5)\(m_1=1\) saa\((1,0)\) na\(m_2=4\) saa\((0,1)\)

    6)\(m_1=1\) saa\((1,0)\) na\(m_2=3\) saa\((2,2)\)

    Jibu
    \(\left(\frac{7}{4},\,\frac{3}{2}\right)\)

    Katika mazoezi ya 7 - 16, compute katikati ya molekuli\(\bar x.\)

    7)\(ρ=1\) kwa\(x∈(−1,3)\)

    8)\(ρ=x^2\) kwa\(x∈(0,L)\)

    Jibu
    \(\dfrac{3L}{4}\)

    9)\(ρ=1\) kwa\(x∈(0,1)\) na\(ρ=2\) kwa\(x∈(1,2)\)

    10)\(ρ=\sin x\) kwa\(x∈(0,π)\)

    Jibu
    \(\frac{π}{2}\)

    11)\(ρ=\cos x\) kwa\(x∈\left(0,\frac{π}{2}\right)\)

    12)\(ρ=e^x\) kwa\(x∈(0,2)\)

    Jibu
    \(\dfrac{e^2+1}{e^2−1}\)

    13)\(ρ=x^3+xe^{−x}\) kwa\(x∈(0,1)\)

    14)\(ρ=x\sin x\) kwa\(x∈(0,π)\)

    Jibu
    \(\dfrac{π^2−4}{π}\)

    15)\(ρ=\sqrt{x}\) kwa\(x∈(1,4)\)

    16)\(ρ=\ln x\) kwa\(x∈(1,e)\)

    Jibu
    \(\frac{1}{4}(1+e^2)\)

    Katika mazoezi 17-19, compute katikati ya wingi\((\bar{x},\bar{y}).\) Matumizi ulinganifu kusaidia Machapisho katikati ya wingi wakati wowote iwezekanavyo.

    17)\(ρ=7\) katika mraba\(0≤x≤1, \; 0≤y≤1\)

    18)\(ρ=3\) katika pembetatu na vipeo\((0,0), \, (a,0)\), na\((0,b)\)

    Jibu
    \(\left(\frac{a}{3},\, \frac{b}{3}\right)\)

    19)\(ρ=2\) kwa ajili ya mkoa umepakana na\(y=\cos(x), \; y=−\cos(x), \; x=−\frac{π}{2}\), na\(x=\frac{π}{2}\)

    Katika mazoezi 20-26, tumia calculator kuteka kanda, halafu ukokotoa katikati ya wingi\((\bar{x},\bar{y}).\) Tumia ulinganifu ili kusaidia Machapisho katikati ya molekuli wakati wowote iwezekanavyo.

    20) [T] Mkoa umepakana na\(y=\cos(2x), \; x=−\frac{π}{4}\), na\(x=\frac{π}{4}\)

    Jibu
    \(\left(0,\frac{π}{8}\right)\)

    21) [T] mkoa kati\(y=2x^2, \; y=0, \; x=0,\) na\(x=1\)

    22) [T] mkoa kati\(y=\frac{5}{4}x^2\) na\(y=5\)

    Jibu
    \((0,3)\)

    23) [T] Mkoa kati\(y=\sqrt{x}, \; y=\ln x, \; x=1,\) na\(x=4\)

    24) [T] Mkoa umepakana\(y=0\) na\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)

    Jibu
    \(\left(0,\frac{4}{π}\right)\)

    25) [T] Mkoa umepakana\(y=0, \; x=0,\) na\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)

    26) [T] Mkoa umepakana\(y=x^2\) na\(y=x^4\) katika roboduara ya kwanza

    Jibu
    \(\left(\frac{5}{8},\, \frac{1}{3}\right)\)

    Katika mazoezi 27 - 31, tumia theorem ya Pappus kuamua kiasi cha sura.

    27)\(y=mx\) Kuzunguka karibu\(x\) -mhimili kati\(x=0\) na\(x=1\)

    28)\(y=mx\) Kuzunguka karibu\(y\) -mhimili kati\(x=0\) na\(x=1\)

    Jibu
    \(V = \frac{mπ}{3}\)vitengo ³

    29) Koni ya jumla iliyoundwa na kupokezana pembetatu na vertices\((0,0), \, (a,0),\) na\((0,b)\) kuzunguka\(y\) -axis. Je! Jibu lako linakubaliana na kiasi cha koni?

    30) Silinda ya jumla iliyoundwa na kupokezana mstatili na vipeo\((0,0), \, (a,0), \, (0,b),\) na\((a,b)\) karibu na\(y\) -axis. Je, jibu lako linakubaliana na kiasi cha silinda?

    Jibu
    \(V = πa^2b\)vitengo ³

    31) Sifa iliyoundwa na kupokezana semicircle na radius\(a\) karibu\(y\) -axis. Je! Jibu lako linakubaliana na kiasi cha nyanja?

    Katika mazoezi 32 - 36, tumia calculator kuteka kanda iliyofungwa na safu. Pata eneo hilo\(M\) na centroid\((\bar{x},\bar{y})\) kwa maumbo yaliyotolewa. Tumia ulinganifu ili kusaidia Machapisho katikati ya wingi wakati wowote iwezekanavyo.

    32) [T] Robo-mduara:\(y=\sqrt{1−x^2}, \; y=0\), na\(x=0\)

    Jibu
    \(\left(\frac{4}{3π},\, \frac{4}{3π}\right)\)

    33) [T] Triangle:\(y=x, \; y=2−x\), na\(y=0\)

    34) [T] Lens:\(y=x^2\) na\(y=x\)

    Jibu
    \(\left(\frac{1}{2},\, \frac{2}{5}\right)\)

    35) [T] Gonga:\(y^2+x^2=1\) na\(y^2+x^2=4\)

    36) [T] Nusu-pete:\(y^2+x^2=1, \; y^2+x^2=4,\) na\(y=0\)

    Jibu
    \(\left(0,\, \frac{28}{9π}\right)\)

    37) Pata kituo cha jumla cha wingi katika sliver kati\(y=x^a\)\(y=x^b\) na\(a>b\). Kisha, tumia theorem ya Pappus ili kupata kiasi cha imara kilichozalishwa wakati unaozunguka\(y\) -axis.

    38) Pata kituo cha jumla cha wingi kati\(y=a^2−x^2, \; x=0\), na\(y=0\). Kisha, tumia theorem ya Pappus ili kupata kiasi cha imara kilichozalishwa wakati unaozunguka\(y\) -axis.

    Jibu
    Kituo cha wingi:\(\left(\frac{a}{6},\,\frac{4a^2}{5}\right),\)
    Volume:\(\dfrac{2πa^4}{9}\) vitengo ³

    39) Pata kituo cha jumla cha wingi kati\(y=b\sin(ax),\; x=0,\) na\(x=\dfrac{π}{a}.\) kisha, tumia theorem ya Pappus ili kupata kiasi cha imara kilichozalishwa wakati unaozunguka\(y\) -axis.

    40) Tumia theorem ya Pappus kupata kiasi cha torus (picha hapa). Fikiria kwamba disk ya radius\(a\) imewekwa na mwisho wa kushoto wa mduara\(x=b, \, b>0,\) na imezungushwa karibu na\(y\) -axis.

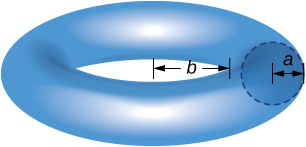
    Takwimu hii ni torus. Ina radius ya ndani ya b. ndani ya torus ni sehemu ya msalaba yaani mduara. Mduara una radius a.

    Jibu
    Volym:\(V = 2\pi^2a^2(b+a)\)

    41) Pata katikati ya wingi\((\bar{x},\bar{y})\) kwa waya nyembamba kando ya semicircle\(y=\sqrt{1−x^2}\) na wingi wa kitengo. (Kidokezo: Tumia theorem ya Pappus.)