6.6: Moments na Vituo vya Misa

Malengo ya kujifunza

• Kupata katikati ya wingi wa vitu kusambazwa kando ya mstari.
• Pata katikati ya wingi wa sahani nyembamba.
• Tumia ulinganifu ili kusaidia kupata centroid ya sahani nyembamba.
• Tumia theorem ya Pappus kwa kiasi.

Katika sehemu hii, tunazingatia vituo vya wingi (pia huitwa centroids, chini ya hali fulani) na wakati. Wazo la msingi la katikati ya wingi ni wazo la uhakika wa kusawazisha. Wengi wetu tumeona wasanii ambao hupiga sahani kwenye mwisho wa vijiti. Wasanii wanajaribu kuweka kadhaa yao kugeuka bila kuruhusu yeyote kati yao kuacha. Ikiwa tunaangalia sahani moja (bila kuifuta), kuna doa tamu kwenye sahani ambako inalingana kikamilifu kwenye fimbo. Ikiwa tunaweka fimbo mahali popote isipokuwa doa hiyo tamu, sahani haina usawa na huanguka chini. (Ndiyo sababu wasanii wanazunguka sahani; spin husaidia kuweka sahani kuanguka hata kama fimbo si hasa mahali pa haki.) Hesabu, kwamba doa tamu inaitwa katikati ya wingi wa sahani.

Katika sehemu hii, sisi kwanza kuchunguza dhana hizi katika muktadha moja-dimensional, kisha kupanua maendeleo yetu ya kuzingatia vituo vya wingi wa mikoa mbili-dimensional na ulinganifu. Mwisho, tunatumia centroids kupata kiasi cha yabisi fulani kwa kutumia theorem ya Pappus.

Kituo cha Misa na Moments

Hebu tuanze kwa kuangalia katikati ya wingi katika muktadha wa mwelekeo mmoja. Fikiria waya mrefu, nyembamba au fimbo ya molekuli isiyofaa kupumzika kwenye fulcrum, kama inavyoonekana kwenye Mchoro\(\PageIndex{1a}\). Sasa tuseme sisi kuweka vitu kuwa\(m_1\) na raia na\(m_2\) katika umbali\(d_1\) na\(d_2\) kutoka fulcrum, kwa mtiririko huo, kama inavyoonekana katika Kielelezo\(\PageIndex{1b}\).

Kielelezo\(\PageIndex{1}\): (a) Fimbo nyembamba inakaa juu ya fulcrum. (b) Misa huwekwa kwenye fimbo.

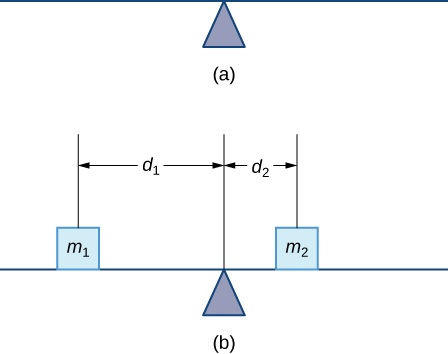
Mfano wa kawaida wa maisha halisi ya mfumo kama huu ni uwanja wa michezo, au teeter-totter, na watoto wa uzito tofauti wameketi umbali tofauti kutoka katikati. Kwenye mteremko, ikiwa mtoto mmoja anakaa kila mwisho, mtoto mzito huzama chini na mtoto mwepesi huinuliwa hewa. Kama mtoto nzito slides katika kuelekea katikati, ingawa, mizani seesaw. Kutumia dhana hii kwa raia juu ya fimbo, tunaona kwamba raia husawaziana ikiwa na tu ikiwa

\[m_1d_1=m_2d_2. \nonumber \]

Kielelezo\(\PageIndex{2}\): Katikati ya wingi\(\bar{x}\) ni hatua ya usawa wa mfumo.

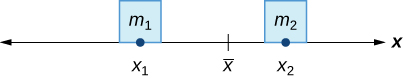
Katika mfano wa seesaw, sisi uwiano mfumo kwa kusonga raia (watoto) kwa heshima na fulcrum. Hata hivyo, tunavutiwa sana na mifumo ambayo raia hawaruhusiwi kuhamia, na badala yake tunaimarisha mfumo kwa kusonga fulcrum. Tuseme tuna raia mbili za uhakika,\(m_1\) na\(m_2\), ziko kwenye mstari wa nambari kwenye pointi\(x_1\) na\(x_2\), kwa mtiririko huo (Kielelezo\(\PageIndex{2}\)). Katikati ya wingi\(\bar{x}\),, ni hatua ambapo fulcrum inapaswa kuwekwa ili kufanya usawa wa mfumo.

Hivyo, tuna

\[ \begin{align*} m_1|x_1−\bar{x}| &=m_2|x_2−\bar{x}| \\[4pt] m_1(\bar{x}−x_1) &=m_2(x_2−\bar{x}) \\[4pt] m_1\bar{x}−m_1x_1 &=m_2x_2−m_2\bar{x} \\[4pt] \bar{x}(m_1+m_2) &=m_1x_1+m_2x_2 \end{align*} \nonumber \]

au

\[ \bar{x} =\dfrac{m_1x_1+m_2x_2}{m_1+m_2} \label{COM} \]

Maneno katika nambari ya Equation\ ref {COM}\(m_1x_1+m_2x_2\),, inaitwa dakika ya kwanza ya mfumo kuhusiana na asili. Ikiwa muktadha ni wazi, mara nyingi tunatupa neno kwanza na tu kutaja maneno haya kama wakati wa mfumo. Maneno katika denominator,\(m_1+m_2\), ni molekuli jumla ya mfumo. Hivyo, katikati ya wingi wa mfumo ni hatua ambayo molekuli jumla ya mfumo inaweza kujilimbikizia bila kubadilisha wakati.

Wazo hili sio mdogo tu kwa raia wawili wa uhakika. Kwa ujumla, kama\(n\) raia,\(m_1,m_2,…,m_n,\) huwekwa kwenye mstari wa nambari\(x_1,x_2,…,x_n,\) kwa pointi kwa mtiririko huo, basi katikati ya wingi wa mfumo hutolewa na

\[ \bar{x}=\dfrac{\displaystyle {\sum_{i=1}^nm_ix_i}}{\displaystyle {\sum_{i=1}^nm_i}} \nonumber \]

Kituo cha Misa ya Vitu kwenye Line

Hebu\(m_1,m_2,…,m_n\) kuwa raia wa uhakika uliowekwa kwenye mstari wa nambari kwenye pointi\(x_1,x_2,…,x_n\), kwa mtiririko huo, na hebu\(\displaystyle m=\sum_{i=1}^nm_i\) ueleze jumla ya mfumo. Kisha, wakati wa mfumo kwa heshima na asili hutolewa na

\[M=\sum_{i=1}^nm_ix_i \label{moment} \]

na katikati ya wingi wa mfumo hutolewa na

\[\bar{x}=\dfrac{M}{m}. \label{COM2a} \]

Tunatumia theorem hii katika mfano wafuatayo.

Mfano\(\PageIndex{1}\): Finding the Center of Mass of Objects along a Line

Tuseme raia nne uhakika ni kuwekwa kwenye mstari namba kama ifuatavyo:

• \(m_1=30\,kg,\)kuwekwa katika\(x_1=−2m\)
• \(m_2=5\,kg,\)kuwekwa katika\(x_2=3m\)
• \(m_3=10\,kg,\)kuwekwa katika\(x_3=6m\)
• \(m_4=15\,kg,\)kuwekwa katika\(x_4=−3m.\)

Suluhisho

Pata wakati wa mfumo kwa heshima na asili na kupata kituo cha wingi wa mfumo.

Kwanza, tunahitaji kuhesabu wakati wa mfumo (Equation\ ref {moment}):

\[ \begin{align*} M &=\sum_{i=1}^4m_ix_i \\[4pt] &= −60+15+60−45 \\[4pt] &=−30. \end{align*}\]

Sasa, ili kupata kituo cha wingi, tunahitaji molekuli jumla ya mfumo:

\[ \begin{align*} m &=\sum_{i=1}^4m_i \\[4pt] &=30+5+10+15 \\[4pt] &= 60\, kg \end{align*}\]

Kisha tuna (kutoka Equation\ ref {com2a})

\(\bar{x}–=\dfrac{M}{m}=−\dfrac{30}{60}=−\dfrac{1}{2}\).

Katikati ya molekuli iko 1/2 m upande wa kushoto wa asili.

Zoezi\(\PageIndex{1}\)

Tuseme raia nne uhakika ni kuwekwa kwenye mstari namba kama ifuatavyo:

• \(m_1=12\,kg\)kuwekwa katika\(x_1=−4m\)
• \(m_2=12\,kg\)kuwekwa katika\(x_2=4m\)
• \(m_3=30\,kg\)kuwekwa katika\(x_3=2m\)
• \(m_4=6\,kg,\)kuwekwa katika\(x_4=−6m.\)

Pata wakati wa mfumo kwa heshima na asili na kupata kituo cha wingi wa mfumo.

Kidokezo

Tumia mchakato kutoka kwa mfano uliopita.

Jibu

\(M=24,\bar{x}=\dfrac{2}{5}m\)

Tunaweza kuzalisha dhana hii ili kupata kituo cha wingi wa mfumo wa raia wa uhakika katika ndege. Hebu\(m_1\) kuwa molekuli uhakika iko\((x_1,y_1)\) katika hatua katika ndege. Kisha wakati\(M_x\) wa wingi kwa heshima na\(x\) -axis hutolewa na\(M_x=m_1y_1\). Vile vile, wakati unaohusiana\(M_y\) na\(y\) -axis hutolewa na

\[M_y=m_1x_1. \nonumber \]

Angalia kwamba\(x\) -kuratibu ya uhakika hutumiwa kuhesabu wakati kwa heshima na\(y\) -axis, na kinyume chake. Sababu ni kwamba\(x\) -kuratibu hutoa umbali kutoka kwa wingi wa uhakika hadi\(y\) -axis, na\(y\) -kuratibu hutoa umbali wa\(x\) -axis (angalia takwimu ifuatayo).

Kielelezo\(\PageIndex{3}\): Point molekuli\(m_1\) iko\((x_1,y_1)\) katika hatua katika ndege.

Ikiwa tuna raia kadhaa wa uhakika katika\(xy\) -ndege, tunaweza kutumia wakati kwa heshima na\(x\) - na\(y\) -axes kuhesabu\(x\) - na\(y\) -kuratibu katikati ya wingi wa mfumo.

Kituo cha Misa ya Vitu katika Ndege

Hebu\(m_1\),\(m_2\),...,\(m_n\) kuwa raia wa uhakika ulio katika\(xy\) -ndege kwenye pointi\((x_1,y_1),(x_2,y_2),…,(x_n,y_n),\) kwa mtiririko huo, na hebu\(\displaystyle m=\sum_{i=1}^nm_i\) ueleze jumla ya mfumo. Kisha wakati\(M_x\) na\(M_y\) wa mfumo kwa heshima na\(x\) - na\(y\) -axes, kwa mtiririko huo, hutolewa na

\[M_x=\sum_{i=1}^nm_iy_i \label{COM1} \]

na

\[M_y=\sum_{i=1}^nm_ix_i. \label{COM2} \]

Pia, kuratibu katikati ya wingi\((\bar{x},\bar{y})\) wa mfumo ni

\[\bar{x}=\dfrac{M_y}{m} \label{COM3} \]

na

\[\bar{y}=\dfrac{M_x}{m}. \label{COM4} \]

Mfano unaofuata unaonyesha jinsi ya katikati ya molekuli formula (Equations\ ref {COM1} -\ ref {COM4}) inaweza kutumika.

Mfano\(\PageIndex{2}\): Finding the Center of Mass of Objects in a Plane

Tuseme raia tatu uhakika ni kuwekwa katika\(xy\) -ndege kama ifuatavyo (kudhani kuratibu ni kutolewa katika mita):

• \(m_1=2\,kg\)kuwekwa katika\((−1,3),\)
• \(m_2=6\,kg\)kuwekwa katika\((1,1),\)
• \(m_3=4\,kg\)kuwekwa katika\((2,−2).\)

Pata katikati ya wingi wa mfumo.

Suluhisho

Kwanza tunahesabu molekuli jumla ya mfumo:

\[m=\sum_{i=1}^3m_i=2+6+4=12\,kg. \nonumber \]

Halafu tunapata wakati kwa heshima na\(x\) - na\(y\) -axes:

\[\begin{align*} M_y &=\sum_{i=1}^3m_ix_i=−2+6+8=12, \\[4pt] M_x &=\sum_{i=1}^3m_iy_i=6+6−8=4. \end{align*}\]

Kisha tuna

\[\bar{x}=\dfrac{M_y}{m}=\dfrac{12}{12}=1 \nonumber \]

na

\[\bar{y}=\dfrac{M_x}{m}=\dfrac{4}{12}=\dfrac{1}{3}. \nonumber \]

Katikati ya wingi wa mfumo ni\((1,1/3),\) katika mita.

Zoezi\(\PageIndex{2}\)

Tuseme raia wa hatua tatu huwekwa kwenye mstari wa nambari kama ifuatavyo (kudhani kuratibu hutolewa kwa mita):

• \(m_1=5\,kg,\)kuwekwa katika\((−2,−3),\)
• \(m_2=3\, kg,\)kuwekwa katika\((2,3),\)
• \(m_3=2\, kg,\)kuwekwa katika\((−3,−2).\)

Pata katikati ya wingi wa mfumo.

Kidokezo

Tumia mchakato kutoka kwa mfano uliopita.

Jibu

\((−1,−1)\)m

Kituo cha Misa ya Sahani nyembamba

Hadi sasa tumeangalia mifumo ya raia wa uhakika kwenye mstari na katika ndege. Sasa, badala ya kuwa na wingi wa mfumo uliojilimbikizia kwenye pointi za kipekee, tunataka kuangalia mifumo ambayo umati wa mfumo unasambazwa kwa kuendelea kwenye karatasi nyembamba ya nyenzo. Kwa madhumuni yetu, tunadhani karatasi ni nyembamba ya kutosha kwamba inaweza kutibiwa kama ni mbili-dimensional. Karatasi hiyo inaitwa lamina. Halafu tunaendeleza mbinu za kupata katikati ya wingi wa lamina. Katika sehemu hii, sisi pia tunadhani wiani wa lamina ni mara kwa mara.

Laminas mara nyingi huwakilishwa na kanda mbili-dimensional katika ndege. Kituo cha kijiometri cha mkoa huo kinaitwa centroid yake. Kwa kuwa tumefikiri wiani wa lamina ni mara kwa mara, katikati ya wingi wa lamina inategemea tu sura ya eneo linalofanana katika ndege; haitegemei wiani. Katika kesi hiyo, katikati ya wingi wa lamina inafanana na centroid ya mkoa uliowekwa katika ndege. Kama ilivyo na mifumo ya raia wa uhakika, tunahitaji kupata umati wa jumla wa lamina, pamoja na wakati wa lamina kuhusiana na\(x\) - na\(y\) -axes.

Sisi kwanza tunazingatia lamina katika sura ya mstatili. Kumbuka kwamba katikati ya wingi wa lamina ni hatua ambapo mizani ya lamina. Kwa mstatili, hatua hiyo ni kituo cha usawa na wima cha mstatili. Kulingana na ufahamu huu, ni wazi kwamba katikati ya wingi wa lamina mstatili ni hatua ambapo diagonals intersect, ambayo ni matokeo ya kanuni ya ulinganifu, na imeelezwa hapa bila ushahidi.

Kanuni ya Ulinganifu

Ikiwa kanda\(R\) ni sawa na mstari\(l\), basi centroid ya\(R\) uongo juu\(l\).

Hebu tugeuke kwenye laminas zaidi ya jumla. Tuseme tuna lamina iliyofungwa hapo juu na grafu ya kazi inayoendelea\(f(x)\), chini na\(x\) -axis, na upande wa kushoto na kulia na mistari\(x=a\) na\(x=b\), kwa mtiririko huo, kama inavyoonekana katika takwimu zifuatazo.

Kielelezo\(\PageIndex{4}\): Kanda katika ndege inayowakilisha lamina.

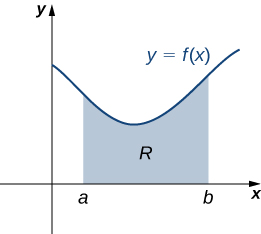
Kama ilivyo na mifumo ya raia wa uhakika, ili kupata katikati ya wingi wa lamina, tunahitaji kupata umati wa jumla wa lamina, pamoja na wakati wa lamina kuhusiana na\(x\) - na\(y\) -axes. Kama tulivyofanya mara nyingi kabla, tunakaribia kiasi hiki kwa kugawanya muda\([a,b]\) na kujenga rectangles.

Kwa\(i=0,1,2,…,n,\) hebu\(P={x_i}\) kuwa kizigeu mara kwa mara ya\([a,b]\). Kumbuka kwamba tunaweza kuchagua hatua yoyote ndani ya muda\([x_{i−1},x_i]\) kama yetu\(x^∗_i\). Katika kesi hii,\(x^∗_i\) tunataka kuwa x -kuratibu ya centroid ya rectangles yetu. Hivyo, kwa\(i=1,2,…,n\), sisi kuchagua\(x^∗_i∈[x_{i−1},x_i]\) vile kwamba\(x^∗_i\) ni midpoint ya muda. Hiyo ni,\(x^∗_i=(x_{i−1}+x_i)/2\). Sasa, kwa\(i=1,2,…,n,\) kujenga mstatili wa urefu\(f(x^∗_i)\) juu Katikati\([x_{i−1},x_i].\) ya wingi wa mstatili huu ni\((x^∗_i,(f(x^∗_i))/2),\) kama inavyoonekana katika takwimu zifuatazo.

Kielelezo\(\PageIndex{5}\): Mstatili wa mwakilishi wa lamina.

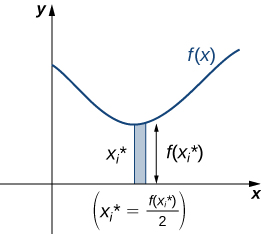
Kisha, tunahitaji kupata molekuli jumla ya mstatili. Hebu\(ρ\) kuwakilisha wiani wa lamina (kumbuka kuwa\(ρ\) ni mara kwa mara). Katika kesi hii,\(ρ\) inaelezwa kwa suala la wingi kwa eneo la kitengo. Hivyo, ili kupata molekuli jumla ya mstatili, tunazidisha eneo la mstatili na\(ρ\). Kisha, wingi wa mstatili hutolewa na\(ρf(x^∗_i)Δx\).

Ili kupata molekuli takriban ya lamina, tunaongeza raia wa rectangles zote kupata

\[m≈\sum_{i=1}^nρf(x^∗_i)Δx. \label{eq51} \]

Equation\ ref {eq51} ni jumla ya Riemann. Kuchukua kikomo kama\(n→∞\) inatoa molekuli halisi ya lamina:

\[ \begin{align*} m &=\lim_{n→∞}\sum_{i=1}^nρf(x^∗_i)Δx \\[4pt] &=ρ∫^b_af(x)dx. \end{align*}\]

Kisha, tunahesabu wakati wa lamina kwa heshima ya x-axis. Kurudi kwa mstatili mwakilishi, kukumbuka kituo chake cha molekuli ni\((x^∗_i,(f(x^∗_i))/2)\). Kumbuka pia kwamba kutibu mstatili kama ni molekuli ya uhakika iko katikati ya wingi haubadili wakati. Hivyo, wakati wa mstatili kwa heshima ya x-axis hutolewa na wingi wa mstatili\(ρf(x^∗_i)Δx\), umeongezeka kwa umbali kutoka katikati ya wingi hadi x-axis:\((f(x^∗_i))/2\). Kwa hiyo, wakati kuhusiana na x-mhimili wa mstatili ni\(ρ([f(x^∗_i)]^2/2)Δx.\) Kuongeza muda wa rectangles na kuchukua kikomo cha jumla ya Riemann inayosababisha, tunaona kwamba wakati wa lamina kuhusiana na x-axis ni

\[ \begin{align*}M_x &=\lim_{n→∞}\sum_{i=1}^nρ\dfrac{[f(x^∗_i)]^2}{2}Δx \\[4pt] &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx.\end{align*}\]

Tunapata wakati huo kwa heshima ya mhimili wa y sawa, akibainisha kuwa umbali kutoka katikati ya wingi wa mstatili hadi y -axis ni\(x^∗_i\). Kisha wakati wa lamina kwa heshima ya y -axis hutolewa na

\[ \begin{align*}M_y &=\lim_{n→∞}\sum_{i=1}^nρx^∗_if(x^∗)i)Δx\\[4pt] &=ρ∫^b_axf(x)dx.\end{align*}\]

Tunapata kuratibu za katikati ya wingi kwa kugawanya wakati kwa wingi wa jumla kutoa\(\bar{x}=M_y/m\) na\(\bar{y}=M_x/m\). Kama sisi kuangalia kwa karibu katika maneno kwa\(M_x,M_y\), na\(m\), tunaona kwamba mara kwa mara\(ρ\) cancels nje wakati\(\bar{x}\) na\(\bar{y}\) ni mahesabu.

Sisi muhtasari matokeo haya katika theorem zifuatazo.

Kituo cha Misa ya Bamba nyembamba katika ndege ya XY

Hebu R inaashiria eneo lililofungwa hapo juu na grafu ya kazi inayoendelea\(f(x)\), chini na x -axis, na upande wa kushoto na kulia kwa mistari\(x=a\) na\(x=b\), kwa mtiririko huo. Hebu\(ρ\) kuashiria wiani wa lamina inayohusishwa. Kisha tunaweza kufanya kauli zifuatazo:

1. Masi ya lamina ni\[m=ρ∫^b_af(x)dx. \label{eq4a} \]
2. Wakati\(M_x\) na\(M_y\) ya lamina kwa heshima ya x - na y -axes, kwa mtiririko huo, ni\[M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx\label{eq4b} \] na\[M_y=ρ∫^b_axf(x)dx.\label{eq4c} \]
3. Kuratibu katikati ya wingi\((\bar{x},\bar{y})\) ni\[\bar{x}=\dfrac{M_y}{m} \label{eq4d} \] na\[\bar{y}=\dfrac{M_x}{m}. \label{eq4e} \]

Katika mfano unaofuata, tunatumia theorem hii ili kupata katikati ya wingi wa lamina.

Mfano\(\PageIndex{3}\): Finding the Center of Mass of a Lamina

Hebu R iwe kanda iliyofungwa hapo juu na grafu ya kazi\(f(x)=\sqrt{x}\) na chini na x -axis juu ya muda\([0,4]\). Pata centroid ya kanda.

Suluhisho

Mkoa unaonyeshwa katika takwimu zifuatazo.

Kielelezo\(\PageIndex{6}\): Kutafuta katikati ya wingi wa lamina.

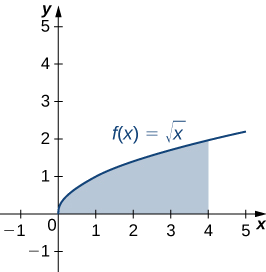
Kwa kuwa tunaulizwa tu kwa centroid ya kanda, badala ya wingi au wakati wa lamina inayohusishwa, tunajua mara kwa mara wiani\(ρ\) kufuta nje ya mahesabu hatimaye. Kwa hiyo, kwa ajili ya urahisi, hebu tufikiri\(ρ=1\).

Kwanza, tunahitaji kuhesabu molekuli jumla (Equation\ ref {eq4a}):

\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^4_0\sqrt{x}dx \\[4pt] &=\dfrac{2}{3}x^{3/2}∣^4_0 \\[4pt] &=\dfrac{2}{3}[8−0] \\[4pt] &=\dfrac{16}{3}. \end{align*}\]

Kisha, tunahesabu wakati (Equation\ ref {eq4d}):

\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=∫^4_0\dfrac{x}{2}dx \\[4pt] &=\dfrac{1}{4}x^2∣^4_0 \\[4pt] &=4 \end{align*}\]

na (Equation\ ref {eq4c}):

\[ \begin{align*} M_y &=ρ∫^b_axf(x)dx \\[4pt] &=∫^4_0x\sqrt{x}dx \\[4pt] &=∫^4_0x^{3/2}dx \\[4pt] &=\dfrac{2}{5}x^{5/2}∣^4_0 \\[4pt] &=\dfrac{2}{5}[32−0] \\[4pt] &=\dfrac{64}{5}. \end{align*}\]

Hivyo, tuna (Equation\ ref {eq4d}):

\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m} \\[4pt] &=\dfrac{64/5}{16/3} \\[4pt] &=\dfrac{64}{5}⋅\dfrac{3}{16} \\[4pt] &=\dfrac{12}{5} \end{align*}\]

na (Equation\ ref {eq4e}):

\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y} \\[4pt] &=\dfrac{4}{16/3} \\[4pt] &=4⋅\dfrac{3}{16} \\[4pt] &=\dfrac{3}{4}. \end{align*}\]

Centroid ya mkoa ni\((12/5,3/4).\)

Zoezi\(\PageIndex{3}\)

Hebu\(R\) kuwa kanda imefungwa hapo juu na grafu ya kazi\(f(x)=x^2\) na chini na x -axis juu ya muda\([0,2].\) Pata centroid ya kanda.

Kidokezo

Tumia mchakato kutoka kwa mfano uliopita.

Jibu

Centroid ya mkoa ni\((3/2,6/5).\)

Tunaweza kukabiliana na njia hii ili kupata centroids ya mikoa ngumu zaidi pia. Tuseme kanda yetu imepakana juu na grafu ya kazi ya kuendelea\(f(x)\), kama kabla, lakini sasa, badala ya kuwa chini amefungwa kwa kanda kuwa x -axis, tuseme kanda imepakana chini na grafu ya pili kuendelea kazi\(g(x)\), kama inavyoonekana katika Kielelezo\(\PageIndex{7}\).

Kielelezo\(\PageIndex{7}\): Mkoa kati ya kazi mbili.

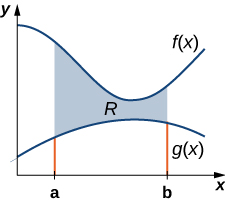
Tena, tunagawanya muda\([a,b]\) na kujenga rectangles. Mstatili wa mwakilishi unaonyeshwa kwenye Kielelezo\(\PageIndex{8}\).

Kielelezo\(\PageIndex{8}\): Mstatili mwakilishi wa kanda kati ya kazi mbili.

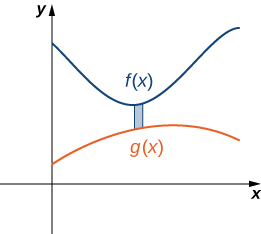
Kumbuka kwamba centroid ya mstatili huu ni\((x^∗_i,(f(x^∗_i)+g(x^∗_i))/2)\). Hatutaweza kupitia maelezo yote ya maendeleo ya jumla ya Riemann, lakini hebu tuangalie baadhi ya hatua muhimu. Katika maendeleo ya formula kwa wingi wa lamina na wakati kuhusiana na y -axis, urefu wa kila mstatili hutolewa na\(f(x^∗_i)−g(x^∗_i)\), ambayo inaongoza kwa kujieleza\(f(x)−g(x)\) katika integrands.

Katika maendeleo ya formula kwa muda kwa heshima ya x-axis, wakati wa kila mstatili hupatikana kwa kuzidisha eneo la mstatili,\(ρ[f(x^∗_i)−g(x^∗_i)]Δx,\) kwa umbali wa centroid kutoka\(x\) -axis\((f(x^∗_i)+g(x^∗_i))/2\), ambayo inatoa\(ρ(1/2){[f(x^∗_i)]^2−[g(x^∗_i)]^2}Δx\). Kuzingatia matokeo haya, tunawasili kwenye theorem ifuatayo.

Kituo cha Misa ya Lamina Imepakana na Kazi mbili

Hebu\(R\) kuashiria eneo lililofungwa hapo juu na grafu ya kazi inayoendelea\(f(x),\) chini na grafu ya kazi inayoendelea\(g(x)\), na upande wa kushoto na kulia kwa mistari\(x=a\) na\(x=b\), kwa mtiririko huo. Hebu\(ρ\) kuashiria wiani wa lamina inayohusishwa. Kisha tunaweza kufanya kauli zifuatazo:

1. Masi ya lamina ni\[m=ρ∫^b_a[f(x)−g(x)]dx. \nonumber \]
2. Wakati\(M_x\) na\(M_y\) ya lamina kwa heshima ya x- na y-axes, kwa mtiririko huo, ni\[M_x=ρ∫^b_a12([f(x)]^2−[g(x)]^2)dx \nonumber \] na\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
3. Kuratibu katikati ya wingi\(\bar{x},\bar{y})\) ni\[\bar{x}=\dfrac{M_y}{m} \nonumber \] na\[\bar{y}=\dfrac{M_x}{m} \nonumber \]

Tunaonyesha theorem hii katika mfano wafuatayo.

Mfano\(\PageIndex{4}\): Finding the Centroid of a Region Bounded by Two Functions

Hebu R iwe kanda iliyofungwa hapo juu na grafu ya kazi\(f(x)=1−x^2\) na chini na grafu ya kazi\(g(x)=x−1.\) Pata centroid ya kanda.

Suluhisho

Mkoa unaonyeshwa katika takwimu zifuatazo.

Kielelezo\(\PageIndex{9}\): Kutafuta centroid ya kanda kati ya curves mbili.

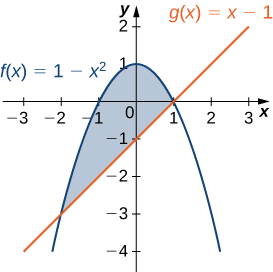
Grafu za kazi zinaingiliana\((−2,−3)\) na\((1,0)\), kwa hiyo tunaunganisha kutoka -1 hadi 1. Mara nyingine tena, kwa ajili ya urahisi, fikiria\(ρ=1\).

Kwanza, tunahitaji kuhesabu molekuli jumla:

\[ \begin{align*} m &=ρ∫^b_a[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}[1−x^2−(x−1)]dx \\[4pt] &=∫^1_{−2}(2−x^2−x)dx \\[4pt] &=\left[2x−\dfrac{1}{3}x^3−\dfrac{1}{2}x^2\right]∣^1_{−2} \\[4pt] &=\left[2−\dfrac{1}{3}−\dfrac{1}{2}\right]−\left[−4+\dfrac{8}{3}−2\right]\\[4pt] &=\dfrac{9}{2}. \end{align*}\]

Kisha, tunahesabu wakati:

\[ \begin{align*} M_x&=ρ∫^b_a\dfrac{1}{2}([f(x)]^2−[g(x)]^2)dx \\[4pt] &=\dfrac{1}{2}∫^1_{−2}((1−x^2)^2−(x−1)^2)dx\\[4pt] &=\dfrac{1}{2}∫^1_{−2}(x^4−3x^2+2x)dx \\[4pt] &=\dfrac{1}{2} \left[\dfrac{x^5}{5}−x^3+x^2\right]∣^1_{−2}\\[4pt] &=−\dfrac{27}{10} \end{align*}\]

na

\[ \begin{align*} M_y &=ρ∫^b_ax[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}x[(1−x^2)−(x−1)]dx\\[4pt] &=∫^1_{−2}x[2−x^2−x]dx\\[4pt] &=∫^1_{−2}(2x−x^4−x^2)dx \\[4pt] &=\left[x^2−\dfrac{x^5}{5}−\dfrac{x^3}{3}\right]∣^1_{−2}\\[4pt] &=−\dfrac{9}{4}. \end{align*}\]

Kwa hiyo, tuna

\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m}\\[4pt] &=−\dfrac{9}{4}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{1}{2} \end{align*}\]

na

\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y}\\[4pt] &=−\dfrac{27}{10}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{3}{5}. \end{align*}\]

Centroid ya mkoa ni\((−(1/2),−(3/5)).\)

Zoezi\(\PageIndex{4}\)

Hebu\(R\) kuwa kanda imefungwa hapo juu na grafu ya kazi\(f(x)=6−x^2\) na chini na grafu ya kazi\(g(x)=3−2x.\) Pata centroid ya kanda.

Kidokezo

Tumia mchakato kutoka kwa mfano uliopita.

Jibu

Centroid ya mkoa ni\((1,13/5).\)

Kanuni ya Ulinganifu

Tulisema kanuni ya ulinganifu mapema, tulipokuwa tukiangalia centroid ya mstatili. Kanuni ya ulinganifu inaweza kuwa msaada mkubwa wakati wa kutafuta centroids ya mikoa ambayo ni sawa. Fikiria mfano unaofuata.

Mfano\(\PageIndex{5}\): Finding the Centroid of a Symmetric Region

Hebu R iwe kanda iliyofungwa hapo juu na grafu ya kazi\(f(x)=4−x^2\) na chini na x-axis. Pata centroid ya kanda.

Suluhisho

Kanda hiyo inaonyeshwa katika takwimu zifuatazo

Kielelezo\(\PageIndex{10}\): Tunaweza kutumia kanuni ya ulinganifu ili kusaidia kupata centroid ya kanda ya ulinganifu.

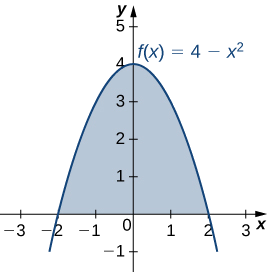
Mkoa huo ni ulinganifu kwa heshima na y -axis. Kwa hiyo, kuratibu x-ya centroid ni sifuri. Tunahitaji tu kuhesabu\(\bar{y}\). Mara nyingine tena, kwa ajili ya urahisi, fikiria\(ρ=1\).

Kwanza, tunahesabu wingi wa jumla:

\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^2_{−2}(4−x^2)dx \\[4pt] &=\left[4x−\dfrac{x^3}{3}\right]∣^2_{−2} \\[4pt] &=\dfrac{32}{3}. \end{align*}\]

Kisha, tunahesabu wakati. Tunahitaji tu\(M_x\):

\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=\dfrac{1}{2}∫^2_{−2}\left[4−x^2\right]^2dx =\dfrac{1}{2}∫^2_{−2}(16−8x^2+x^4)dx \\[4pt] &=\dfrac{1}{2}\left[\dfrac{x^5}{5}−\dfrac{8x^3}{3}+16x\right]∣^2_{−2}=\dfrac{256}{15} \end{align*}\]

Kisha tuna

\[\bar{y}=\dfrac{M_x}{y}=\dfrac{256}{15}⋅\dfrac{3}{32}=\dfrac{8}{5}. \nonumber \]

Centroid ya mkoa ni\((0,8/5).\)

Zoezi\(\PageIndex{5}\)

Hebu\(R\) kuwa kanda imefungwa hapo juu na grafu ya kazi\(f(x)=1−x^2\) na chini na\(x\) -axis. Pata centroid ya kanda.

Kidokezo

Tumia mchakato kutoka kwa mfano uliopita.

Jibu

Centroid ya mkoa ni\((0,2/5).\)

Grand Canyon Skywalk

Skywalk ya Grand Canyon ilifunguliwa kwa umma tarehe 28 Machi 2007. Hii ajabu uhandisi ni horseshoe-umbo uchunguzi jukwaa kusimamishwa 4000 ft juu ya Mto Colorado juu ya West Rim ya Grand Canyon. Yake kioo kioo sakafu inaruhusu maoni stunning ya korongo chini (angalia takwimu zifuatazo).

Kielelezo\(\PageIndex{11}\): Grand Canyon Skywalk inatoa maoni mkubwa wa korongo. (mikopo: 10da_ralta, Wikimedia Commons)

Skywalk ni kubuni ya cantilever, maana yake ni kwamba jukwaa la uchunguzi linaendelea juu ya mdomo wa korongo, bila njia inayoonekana ya msaada chini yake. Licha ya ukosefu wa machapisho ya usaidizi inayoonekana au vipande, miundo ya cantilever imeundwa kuwa imara sana na Skywalk sio ubaguzi. Jukwaa la uchunguzi linaunganishwa kwa nguvu ili kusaidia machapisho ambayo yanapanua 46 ft chini ndani ya msingi. Muundo ulijengwa ili kuhimili upepo wa 100-mph na tetemeko la ardhi la ukubwa wa 8.0 ndani ya mi 50, na ina uwezo wa kusaidia zaidi ya lb 70,000,000.

Sababu moja inayoathiri utulivu wa Skywalk ni katikati ya mvuto wa muundo. Tutahesabu katikati ya mvuto wa Skywalk, na kuchunguza jinsi kituo cha mvuto kinabadilika wakati watalii wanatembea kwenye jukwaa la uchunguzi.

Jukwaa la uchunguzi ni U-umbo. Miguu ya U ni upana wa futi 10 na kuanza juu ya ardhi, chini ya kituo cha wageni, 48 ft kutoka makali ya korongo. jukwaa inaenea 70 ft juu ya makali ya korongo.

Ili kuhesabu katikati ya wingi wa muundo, tunachukua kama lamina na kutumia kanda mbili-dimensional katika xy-ndege ili kuwakilisha jukwaa. Tunaanza kwa kugawanya kanda katika subregions tatu ili tuweze kuzingatia kila mkoa tofauti. Mkoa wa kwanza, uliotajwa\(R_1\), una sehemu iliyopigwa ya U. Sisi mfano\(R_1\) kama annulus ya semicircular, na radius ya ndani 25 ft na radius ya nje 35 ft, katikati ya asili (Kielelezo\(\PageIndex{12}\)).

Kielelezo\(\PageIndex{12}\): Sisi mfano Skywalk na mikoa mitatu ndogo.

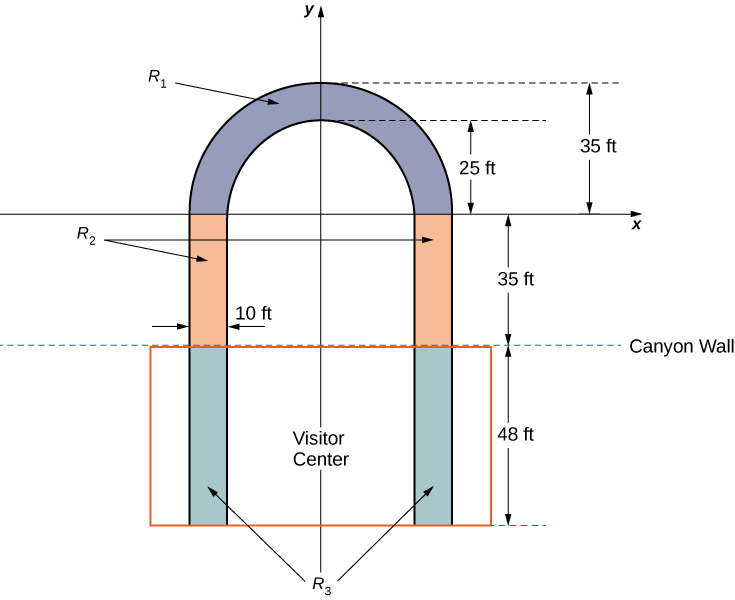
miguu ya jukwaa, kupanua 35 ft kati\(R_1\) na ukuta korongo, wanaunda pili ndogo ya kanda,\(R_2\). Mwisho, mwisho wa miguu, ambayo kupanua 48 ft chini ya kituo cha wageni, wanaunda tatu ndogo ya kanda,\(R_3\). Fikiria wiani wa lamina ni mara kwa mara na kudhani uzito wa jumla wa jukwaa ni 1,200,000 lb (sio pamoja na uzito wa kituo cha wageni; tutazingatia kwamba baadaye). Tumia\(g=32\;ft/sec^2\).

1. Compute eneo la kila moja ya mikoa mitatu ndogo. Kumbuka kwamba maeneo ya mikoa\(R_2\) na\(R_3\) yanapaswa kujumuisha maeneo ya miguu tu, si nafasi ya wazi kati yao. Majibu ya pande zote kwa mguu wa mraba wa karibu.
2. Kuamua wingi unaohusishwa na kila moja ya mikoa mitatu ndogo.
3. Tumia katikati ya wingi wa kila moja ya mikoa mitatu ndogo.
4. Sasa, tibu kila moja ya mikoa mitatu kama molekuli ya uhakika iko katikati ya wingi wa kanda ndogo inayofanana. Kutumia uwakilishi huu, uhesabu katikati ya wingi wa jukwaa lote.
5. Fikiria kituo cha wageni kina uzito wa 2,200,000 lb, na kituo cha wingi sambamba na katikati ya wingi wa\(R_3\) .Kuchukua kituo cha wageni kama molekuli ya uhakika, rejesha katikati ya wingi wa mfumo. Je, katikati ya mabadiliko ya molekuli hubadilikaje?
6. Ingawa Skywalk ilijengwa ili kupunguza idadi ya watu kwenye jukwaa la uchunguzi hadi 120, jukwaa lina uwezo wa kusaidia hadi watu 800 wenye uzito wa lb 200 kila mmoja. Ikiwa watu wote 800 waliruhusiwa kwenye jukwaa, na wote walikwenda mwisho wa jukwaa, kituo cha mvuto wa mfumo kinaathirikaje? (Ni pamoja na kituo cha wageni katika mahesabu na kuwakilisha watu kwa wingi uhakika iko katika makali mbali ya jukwaa, 70 ft kutoka ukuta korongo.)

Theorem ya Pappus

Sehemu hii inaisha na majadiliano ya theorem ya Pappus kwa kiasi, ambayo inaruhusu sisi kupata kiasi cha aina fulani ya yabisi kwa kutumia centroid. (Pia kuna theorem ya Pappus kwa eneo la uso, lakini ni muhimu sana kuliko theorem kwa kiasi.)

Theorem ya Pappus kwa Volume

Hebu\(R\) kuwa kanda katika ndege na basi l kuwa mstari katika ndege ambayo haina intersect\(R\). Kisha kiasi cha imara ya mapinduzi yaliyoundwa na\(R\) kuzunguka l ni sawa na eneo la\(R\) kuongezeka kwa umbali d alisafiri na centroid ya\(R\).

Ushahidi

Tunaweza kuthibitisha kesi wakati kanda imefungwa hapo juu na grafu ya kazi\(f(x)\) na chini na grafu ya kazi\(g(x)\) juu ya muda\([a,b]\), na ambayo mhimili wa mapinduzi ni\(y\) -axis. Katika kesi hiyo, eneo la kanda ni\(\displaystyle A=∫^b_a[f(x)−g(x)]\,dx\). Kwa kuwa mhimili wa mzunguko ni\(y\) -axis, umbali uliosafiri na centroidi ya kanda inategemea tu\(x\) -kuratibu ya centroid\(\bar{x}\), ambayo ni

\[x=\dfrac{M_y}{m}, \nonumber \]

wapi

\[m=ρ∫^b_a[f(x)−g(x)]dx \nonumber \]

na

\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Kisha,

\[d=2π\dfrac{\displaystyle {ρ∫^b_ax[f(x)−g(x)]dx}}{\displaystyle{ρ∫^b_a[f(x)−g(x)]dx}} \nonumber \]

na hivyo

\[d⋅A=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Hata hivyo, kwa kutumia njia ya shells cylindrical, tuna

\[V=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Hivyo,

\[V=d⋅A \nonumber \]

na ushahidi ni kamili.

□

Mfano\(\PageIndex{6}\): Using the Theorem of Pappus for Volume

Hebu\(R\) kuwa mduara wa Radius 2 unaozingatia katika\((4,0).\) Matumizi theorem ya Pappus kwa kiasi ili kupata kiasi cha torus yanayotokana na\(R\) yanazunguka\(y\) -axis.

Suluhisho

Kanda na torus zinaonyeshwa katika takwimu zifuatazo.

Kielelezo\(\PageIndex{13}\): Kuamua kiasi cha torus kwa kutumia theorem ya Pappus. (a) Mkoa wa mviringo\(R\) katika ndege; (b) torus yanayotokana na yanazunguka\(R\) juu ya\(y\) -axis.

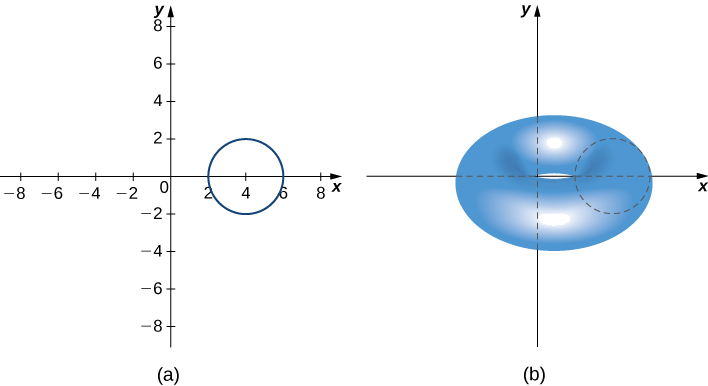
Mkoa\(R\) ni mduara wa radius 2, hivyo eneo la R ni\(A=4π\;\text{units}^2\). Kwa kanuni ya ulinganifu, centroid ya R ni katikati ya mduara. Centroid husafiri kuzunguka\(y\) -axis katika njia ya mviringo ya radius 4, hivyo centroid husafiri\(d=8π\) vitengo. Kisha, kiasi cha torus ni\(A⋅d=32π^2\) vitengo ³.

Zoezi\(\PageIndex{6}\)

Hebu R kuwa mduara wa radius 1 unaozingatia katika\((3,0).\) Matumizi theorem ya Pappus kwa kiasi ili kupata kiasi cha torus yanayotokana na yanazunguka R karibu\(y\) -axis.

Kidokezo

Tumia mchakato kutoka kwa mfano uliopita.

Jibu

\(6π^2\)vitengo ³

Dhana muhimu

• Kihisabati, katikati ya wingi wa mfumo ni hatua ambayo molekuli jumla ya mfumo inaweza kujilimbikizia bila kubadilisha wakati. Kwa kusema, katikati ya wingi inaweza kufikiriwa kama hatua ya kusawazisha ya mfumo.
• Kwa raia wa uhakika kusambazwa kwenye mstari wa nambari, wakati wa mfumo kuhusiana na asili ni\(\displaystyle M=\sum^n_{i=1}m_ix_i.\) Kwa raia wa uhakika kusambazwa katika ndege, wakati wa mfumo kuhusiana na\(x\) - na\(y\) -axes, kwa mtiririko huo, ni\(\displaystyle M_x=\sum^n_{i=1}m_iy_i\) na\(\displaystyle M_y=\sum^n_{i=}m_ix_i\), kwa mtiririko huo.
• Kwa lamina iliyofungwa hapo juu na kazi\(f(x)\), wakati wa mfumo kwa heshima na\(x\) - na\(y\) -axes, kwa mtiririko huo, ni\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) na\(\displaystyle M_y=ρ∫^b_axf(x)\,dx.\)
• \(y\)Kuratibu\(x\) - na -katikati ya molekuli zinaweza kupatikana kwa kugawanya wakati karibu na\(y\) -axis na karibu na\(x\) -axis, kwa mtiririko huo, kwa wingi wa jumla. Kanuni ya ulinganifu inasema kwamba ikiwa kanda ni sawa na heshima na mstari, basi centroid ya kanda iko kwenye mstari.
• Theorem ya Pappus kwa kiasi inasema kwamba ikiwa mkoa unazunguka mhimili wa nje, kiasi cha imara inayosababisha ni sawa na eneo la kanda lililoongezeka kwa umbali uliosafiri na centroid ya kanda.

Mlinganyo muhimu

• Misa ya lamina

\(\displaystyle m=ρ∫^b_af(x)dx\)

• Wakati wa lamina

\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\text{ and }M_y=ρ∫^b_axf(x)\,dx\)

• Kituo cha wingi wa lamina

\(\bar{x}=\dfrac{M_y}{m}\text{ and }\bar{y}=\dfrac{M_x}{m}\)

faharasa

katikati ya molekuli

hatua ambayo molekuli jumla ya mfumo inaweza kujilimbikizia bila kubadilisha wakati

centrroid

centroid ya kanda ni kituo cha kijiometri cha kanda; laminas mara nyingi huwakilishwa na mikoa katika ndege; ikiwa lamina ina wiani wa mara kwa mara, katikati ya wingi wa lamina inategemea tu sura ya eneo linalofanana; katika kesi hii, katikati ya wingi wa lamina inafanana na centroid ya mkoa wa mwakilishi

lamina

karatasi nyembamba ya nyenzo; laminas ni nyembamba ya kutosha kwamba, kwa madhumuni ya hisabati, wanaweza kutibiwa kama ni mbili-dimensional

wakati

ikiwa n raia hupangwa kwenye mstari wa namba, wakati wa mfumo kuhusiana na asili hutolewa na\(\displaystyle M=\sum^n_{i=1}m_ix_i\); ikiwa, badala yake, tunazingatia kanda katika ndege, imefungwa hapo juu na kazi\(f(x)\) kwa muda\([a,b]\), basi wakati wa kanda kwa heshima na\(x\) - na \(y\)-axes hutolewa\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) na\(\displaystyle M_y=ρ∫^b_axf(x)\,dx\), kwa mtiririko huo

kanuni ya ulinganifu

kanuni ya ulinganifu inasema kwamba ikiwa kanda\(R\) ni sawa na mstari\(I\), basi centroid ya\(R\) uongo juu\(I\)

theorem ya Pappus kwa kiasi

theorem hii inasema kwamba kiasi cha imara ya mapinduzi yaliyoundwa na kuzunguka kanda karibu na mhimili wa nje ni sawa na eneo la kanda lililoongezeka kwa umbali uliosafiri na centroid ya kanda