6.7: Integrals, Kazi za Kielelezo, na Logarithms

Malengo ya kujifunza

• Andika ufafanuzi wa logarithm ya asili kama muhimu.
• Tambua derivative ya logarithm ya asili.
• Unganisha kazi zinazohusisha kazi ya asili ya logarithmic.
• Eleza nambari kwa\(e\) njia muhimu.
• Tambua derivative na muhimu ya kazi ya kielelezo.
• Thibitisha mali ya logarithms na kazi za kielelezo kwa kutumia integrals.
• Express jumla logarithmic na exponential kazi katika suala la logarithms asili na exponentials.

Tayari tulichunguza kazi za kielelezo na logarithms katika sura za awali. Hata hivyo, sisi glossed juu ya baadhi ya maelezo muhimu katika majadiliano ya awali. Kwa mfano, hatujifunza jinsi ya kutibu kazi za kielelezo na vielelezo ambavyo havipatikani. Ufafanuzi wa namba e ni eneo lingine ambapo maendeleo ya awali yalikuwa hayajakamilika. Sasa tuna zana za kukabiliana na dhana hizi kwa njia ya hesabu zaidi ukali, na tunafanya hivyo katika sehemu hii.

Kwa madhumuni ya sehemu hii, kudhani sisi bado defined logarithm asili, idadi\(e\), au yoyote ya muungano na tofauti formula kuhusishwa na kazi hizi. Mwishoni mwa sehemu hiyo, tutajifunza dhana hizi kwa njia ya hesabu kali (na tutaona ni sawa na dhana tuliyojifunza mapema). Tunaanza sehemu kwa kufafanua logarithm ya asili kwa suala la muhimu. Ufafanuzi huu huunda msingi wa sehemu hiyo. Kutoka kwa ufafanuzi huu, tunapata fomu za kutofautisha, kufafanua idadi\(e\), na kupanua dhana hizi kwa logarithms na kazi za kielelezo za msingi wowote.

Logarithm Asili kama Integral

Kumbuka utawala wa nguvu kwa integrals:

\[ ∫ x^n \,dx = \dfrac{x^{n+1}}{n+1} + C , \quad n≠−1. \nonumber \]

Kwa wazi, hii haifanyi kazi wakati\(n=−1,\) kama ingeweza kutufanya kugawanya na sifuri. Kwa hiyo, tunafanya nini na\(\displaystyle ∫\dfrac{1}{x}\,dx\)? Kumbuka kutoka Theorem ya msingi ya Calculus kwamba\(\displaystyle ∫^x_1\dfrac{1}{t}dt\) ni antiderivative ya\(\dfrac{1}{x}.\) Kwa hiyo, tunaweza kufanya ufafanuzi ufuatao.

Ufafanuzi: Logarithm Asili

Kwa\(x>0\), kufafanua asili logarithm kazi na

\[\ln x=∫^x_1\dfrac{1}{t}\,dt. \nonumber \]

Kwa\(x>1\), hii ni eneo chini ya Curve\(y=\dfrac{1}{t}\) kutoka\(1\) kwa\(x\). Kwa\(x<1\), tuna

\[ ∫^x_1\dfrac{1}{t}\,dt=−∫^1_x\dfrac{1}{t}\,dt, \nonumber \]

hivyo katika kesi hii ni hasi ya eneo chini ya curve kutoka\(x\) kwa\(1\) (angalia takwimu zifuatazo).

Kielelezo\(\PageIndex{1}\): (a) Wakati\(x>1\), logarithm ya asili ni eneo chini ya pembe\(y=1/t\) kutoka\(1\) kwa\(x\). (b) Wakati\(x<1\), logarithm ya asili ni hasi ya eneo chini ya curve kutoka\(x\) kwa\(1\).

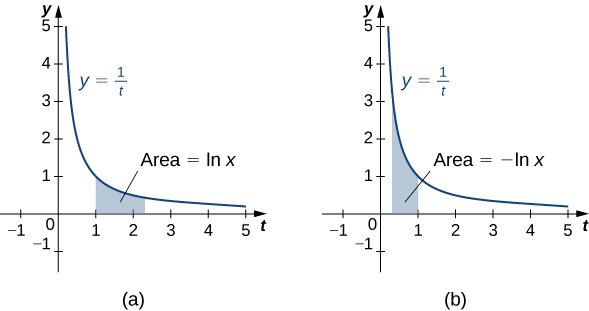
Kumbuka kwamba\(\ln 1=0\). Zaidi ya hayo, kazi\(y=\dfrac{1}{t}>0\) kwa ajili ya\(x>0\). Kwa hiyo, kwa mali ya integrals, ni wazi kwamba\(\ln x\) ni kuongezeka kwa\(x>0\).

Mali ya Logarithm ya Asili

Kwa sababu ya njia tuliyofafanua logarithm ya asili, formula ya kutofautisha ifuatayo inatoka mara moja kama matokeo ya Theorem ya Msingi ya Calculus.

Ufafanuzi: Derivative ya Logarithm Asili

Kwa\(x>0\), derivative ya logarithm ya asili hutolewa na

\[ \dfrac{d}{dx}\Big( \ln x \Big) = \dfrac{1}{x}. \nonumber \]

Corollary kwa derivative ya Logarithm Asili

Kazi\(\ln x\) ni tofauti; kwa hiyo, inaendelea.

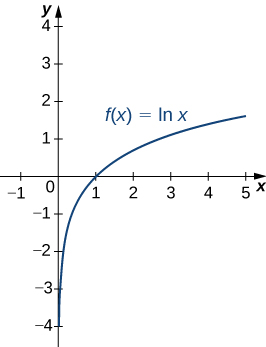
Grafu ya\(\ln x\) inavyoonekana kwenye Kielelezo. Kumbuka kwamba ni kuendelea katika uwanja wake wa\((0,∞)\).

Kielelezo\(\PageIndex{2}\): Grafu ya\(f(x)=\ln x\) inaonyesha kwamba ni kazi inayoendelea.

Mfano\(\PageIndex{1}\): Calculating Derivatives of Natural Logarithms

Tumia derivatives zifuatazo:

1. \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)\)
2. \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)\)

Suluhisho

Tunahitaji kutumia utawala wa mnyororo katika matukio yote mawili.

1. \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)=\dfrac{15x^2}{5x^3−2}\)
2. \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)=\dfrac{2(\ln (3x))⋅3}{3x}=\dfrac{2(\ln (3x))}{x}\)

Zoezi\(\PageIndex{1}\)

Tumia derivatives zifuatazo:

1. \(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)\)
2. \(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)\)

Kidokezo

Tumia fomu ya kutofautisha tu iliyotolewa na utumie utawala wa mnyororo kama inavyohitajika.

Jibu

a.\(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)=\dfrac{4x+1}{2x^2+x}\)

b.\(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)=\dfrac{6\ln (x^3)}{x}\)

Kumbuka kwamba kama sisi kutumia thamani kamili kazi na kujenga kazi mpya\(\ln |x|\), tunaweza kupanua uwanja wa logarithm asili ni pamoja na\(x<0\). Kisha\(\dfrac{d}{dx}\Big( \ln x \Big)=\dfrac{1}{x}\). Hii inatoa kupanda kwa familiar ushirikiano formula.

Integral ya\(\frac{1}{u} \, du\)

Logarithm ya asili ni antiderivative ya kazi\(f(u)=\dfrac{1}{u}\):

\[∫\dfrac{1}{u}\,du=\ln |u|+C. \nonumber \]

Mfano\(\PageIndex{2}\): Calculating Integrals Involving Natural Logarithms

Tumia hesabu muhimu\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx.\)

Suluhisho

Kutumia\(u\) -badala, basi\(u=x^2+4\). Kisha\(du=2x\,dx\) na tuna

\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx=\dfrac{1}{2}∫\dfrac{1}{u}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln |x^2+4|+C=\dfrac{1}{2}\ln (x^2+4)+C.\)

Zoezi\(\PageIndex{2}\)

Tumia hesabu muhimu\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx.\)

Kidokezo

Tumia formula ya ushirikiano iliyotolewa mapema na utumie u-badala kama inavyohitajika.

Jibu

\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx=\dfrac{1}{3}\ln ∣x^3+6∣+C\)

Ingawa sisi kuitwa kazi yetu “logarithm,” sisi si kweli imeonekana kuwa yoyote ya mali ya logarithms kushikilia kwa kazi hii. Tunafanya hivyo hapa.

Mali ya Logarithm ya Asili

Ikiwa\(a,\, b>0\) na\(r\) ni namba ya busara, basi

1. \(\ln 1=0\)
2. \(\ln (ab)=\ln a+\ln b\)
3. \(\ln \left(\dfrac{a}{b}\right)=\ln a−\ln b\)
4. \(\ln \left(a^r\right)=r\ln a\)

Ushahidi

i. kwa ufafanuzi,\(\displaystyle \ln 1=∫^1_1\dfrac{1}{t}\,dt=0.\)

ii. Tuna

\(\displaystyle \ln (ab)=∫^{ab}_1\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt.\)

Matumizi\(u-substitution\) ya muhimu ya mwisho katika maneno haya. Hebu\(u=t/a\). Kisha\(du=(1/a)dt.\) Zaidi ya hayo\(t=a,\, u=1\), wakati, na wakati\(t=ab,\, u=b.\) Hivyo sisi kupata

\(\displaystyle \ln (ab)=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_1\dfrac{a}{t}⋅\dfrac{1}{a}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^b_1\dfrac{1}{u}\,du=\ln a+\ln b.\)

iii. Kumbuka kwamba

\(\dfrac{d}{dx}\Big(\ln (x^r)\Big)=\dfrac{rx^{r−1}}{x^r}=\dfrac{r}{x}\).

Zaidi ya hayo,

\(\dfrac{d}{dx}\Big((r\ln x)\Big)=\dfrac{r}{x}.\)

Kwa kuwa derivatives ya kazi hizi mbili ni sawa, na Theorem ya Msingi ya Calculus, lazima iwe tofauti na mara kwa mara. Hivyo tuna

\(\ln (x^r)=r\ln x+C\)

kwa baadhi ya mara kwa mara\(C\). Kuchukua\(x=1\), tunapata

\(\ln (1^r)=r\ln (1)+C\)

\(0=r(0)+C\)

\(C=0.\)

Hivyo\(\ln (x^r)=r\ln x\) na ushahidi umekamilika. Kumbuka kwamba tunaweza kupanua mali hii kwa maadili irrational ya\(r\) baadaye katika sehemu hii.

Sehemu ya ii. ifuatavyo kutoka sehemu ii. na iv. na ushahidi umesalia kwako.

□

Mfano\(\PageIndex{3}\): Using Properties of Logarithms

Tumia mali ya logarithms ili kurahisisha maneno yafuatayo kwenye logarithm moja:

\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right).\)

Suluhisho

Tuna

\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right)=\ln (3^2)−2 \ln 3+\ln (3^{−1})=2\ln 3−2\ln 3−\ln 3=−\ln 3.\)

Zoezi\(\PageIndex{3}\)

Tumia mali ya logarithms ili kurahisisha maneno yafuatayo kwenye logarithm moja:

\( \ln 8−\ln 2−\ln \left(\tfrac{1}{4}\right)\)

Kidokezo

Tumia mali ya logarithms.

Jibu

\(4\ln 2\)

Kufafanua Idadi e

Sasa kwa kuwa tuna logarithm asili defined, tunaweza kutumia kwamba kazi kufafanua idadi\(e\).

Ufafanuzi:\(e\)

Idadi\(e\) hufafanuliwa kuwa namba halisi kama hiyo

\[\ln e=1\nonumber \]

Ili kuiweka njia nyingine, eneo chini ya pembe\(y=1/t\) kati\(t=1\) na\(t=e\) ni\(1\) (Kielelezo). Ushahidi kwamba idadi hiyo ipo na ni ya kipekee imesalia kwako. (Kidokezo: Tumia Theorem ya Thamani ya Kati ili kuthibitisha kuwepo na ukweli kwamba\(\ln x\) unaongezeka ili kuthibitisha pekee.)

\(\PageIndex{3}\)Kielelezo:Eneo chini ya pembe kutoka hadi\(1\) ni\(e\) sawa na moja.

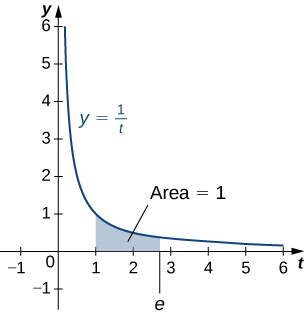
Nambari\(e\) inaweza kuonyeshwa kuwa isiyo na maana, ingawa hatuwezi kufanya hivyo hapa (angalia Mradi wa Wanafunzi katika Taylor na Maclaurin Series). Thamani yake ya takriban hutolewa na

\( e≈2.71828182846.\)

Kazi ya Kielelezo

Sasa tunageuka mawazo yetu kwa kazi\(e^x\). Kumbuka kwamba logarithm ya asili ni moja kwa moja na kwa hiyo ina kazi inverse. Kwa sasa, sisi kuashiria kazi hii inverse na\(\exp x\). Kisha,

\[ \exp(\ln x)=x \nonumber \]

kwa\(x>0\) na

\[ \ln (\exp x)=x \nonumber \]

kwa ajili ya wote\(x\).

Takwimu inayofuata inaonyesha grafu za\(\exp x\) na\(\ln x\).

Kielelezo\(\PageIndex{4}\): Grafu ya\(\ln x\) na\(\exp x\).

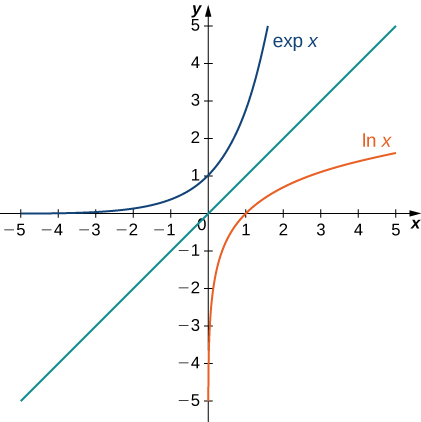
Sisi nadharia kwamba\(\exp x=e^x\). Kwa maadili ya busara ya\(x\), hii ni rahisi kuonyesha. Ikiwa\(x\) ni busara, basi tuna\(\ln (e^x)=x\ln e=x\). Hivyo, wakati\(x\) ni busara,\(e^x=\exp x\). Kwa maadili irrational ya\(x\), sisi tu kufafanua\(e^x\) kama kazi inverse ya\(\ln x\).

Ufafanuzi

Kwa idadi yoyote halisi\(x\),\(y=e^x\) kufafanua kuwa idadi ambayo

\[\ln y=\ln (e^x)=x. \nonumber \]

Basi sisi\(e^x=\exp x\) kwa ajili ya wote\(x\), na hivyo

\(e^{\ln x}=x\)kwa\(x>0\) na\(\ln (e^x)=x\)

kwa ajili ya wote\(x\).

Mali ya Kazi ya Kielelezo

Tangu kazi kielelezo ilielezwa katika suala la kazi inverse, na si katika suala la nguvu ya ni\(e\) lazima kuthibitisha kwamba sheria ya kawaida ya vielelezo kushikilia kwa kazi\(e^x\).

Mali ya Kazi ya Kielelezo

Kama\(p\) na\(q\) ni idadi yoyote halisi na\(r\) ni idadi ya busara, basi

1. \(e^pe^q=e^{p+q}\)
2. \(\dfrac{e^p}{e^q}=e^{p−q}\)
3. \((e^p)^r=e^{pr}\)

Ushahidi

Kumbuka kwamba ikiwa\(p\) na\(q\) ni busara, mali zinashikilia. Hata hivyo, kama\(p\) au\(q\) ni irrational, ni lazima kuomba inverse kazi ufafanuzi wa\(e^x\) na kuthibitisha mali. Tu mali ya kwanza ni kuthibitishwa hapa; wengine wawili ni wa kushoto na wewe. Tuna

\[ \ln (e^pe^q)=\ln (e^p)+\ln (eq)=p+q=\ln (e^{p+q}).\nonumber \]

Kwa kuwa\(\ln x\) ni moja kwa moja, basi

\[ e^pe^q=e^{p+q}.\nonumber \]

□

Kama ilivyo kwa sehemu iv. ya mali logarithm, tunaweza kupanua mali ii. kwa maadili irrational ya\(r\), na sisi kufanya hivyo mwishoni mwa sehemu.

Tunataka pia kuthibitisha formula tofauti kwa ajili ya kazi\(y=e^x\). Ili kufanya hivyo, tunahitaji kutumia tofauti thabiti. Hebu\(y=e^x\). Kisha

\[ \begin{align*} \ln y &=x \\[5pt] \dfrac{d}{dx}\Big(\ln y\Big) &=\dfrac{d}{dx}\Big(x\Big) \\[5pt] \dfrac{1}{y}\dfrac{dy}{dx} &=1 \\[5pt] \dfrac{dy}{dx} &=y. \end{align*}\]

Hivyo, tunaona

\[ \dfrac{d}{dx}\Big(e^x\Big)=e^x \nonumber \]

kama taka, ambayo inaongoza mara moja kwa formula muungano

\[ ∫e^x \,dx=e^x+C. \nonumber \]

Tunatumia kanuni hizi katika mifano ifuatayo.

Mfano\(\PageIndex{4}\): Using Properties of Exponential Functions

Tathmini derivatives zifuatazo:

1. \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)\)
2. \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)\)

Suluhisho

Tunatumia utawala wa mnyororo kama inavyohitajika.

1. \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)=\dfrac{d}{dt}\Big(e^{3t+t^2}\Big)=e^{3t+t^2}(3+2t)\)
2. \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)=e^{3x^2}6x\)

Zoezi\(\PageIndex{4}\)

Tathmini derivatives zifuatazo:

1. \(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)\)
2. \(\dfrac{d}{dt}\Big((e^{2t})^3\Big)\)

Kidokezo

Tumia mali ya kazi za kielelezo na utawala wa mnyororo kama inavyohitajika.

Jibu

a.\(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)=e^{x^{2−5x}}(2x−5)\)

b.\(\dfrac{d}{dt}\Big((e^{2t})^3\Big)=6e^{6t}\)

Mfano\(\PageIndex{5}\): Using Properties of Exponential Functions

Tathmini muhimu yafuatayo:\(\displaystyle ∫2xe^{−x^2}\,dx.\)

Suluhisho

Kutumia\(u\) -badala, basi\(u=−x^2\). Kisha\(du=−2x\,dx,\) na tuna

\(\displaystyle ∫2xe^{−x^2}\,dx=−∫e^u\,du=−e^u+C=−e^{−x^2}+C.\)

Zoezi\(\PageIndex{5}\)

Tathmini muhimu yafuatayo:\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx.\)

Kidokezo

Tumia mali ya kazi za kielelezo na\(u-substitution\) kama inavyohitajika.

Jibu

\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx=−\dfrac{4}{3}e^{−3x}+C\)

Kazi za jumla za Logarithmic na za Kielelezo

Tunakaribia sehemu hii kwa kuangalia kazi za kielelezo na logarithms na misingi zaidi ya\(e\). Kazi za kielelezo ni kazi za fomu\(f(x)=a^x\). Kumbuka kwamba isipokuwa\(a=e\), bado hatuna hesabu ukali ufafanuzi wa kazi hizi kwa watazamaji irrational. Hebu kurekebisha kwamba hapa kwa kufafanua kazi\(f(x)=a^x\) katika suala la kazi kielelezo\(e^x\). Sisi kisha kuchunguza logarithms na besi zaidi ya e kama kazi inverse ya kazi kielelezo.

Ufafanuzi: Kazi ya kielelezo

Kwa yoyote\(a>0,\) na kwa idadi yoyote halisi\(x\), kufafanua\(y=a^x\) kama ifuatavyo:

\[y=a^x=e^{x \ln a}. \nonumber \]

Sasa\(a^x\) hufafanuliwa kwa ukali kwa maadili yote ya\(x\). Ufafanuzi huu pia inaruhusu sisi kuzalisha mali iv. ya logarithms na mali ii. ya kazi kielelezo kuomba maadili wote mantiki na irrational ya\(r\). Ni moja kwa moja kuonyesha kwamba mali ya exponents kushikilia kwa ajili ya kazi ya jumla kielelezo defined kwa njia hii.

Hebu sasa tufanye ufafanuzi huu ili kuhesabu formula ya kutofautisha kwa\(a^x\). Tuna

\(\dfrac{d}{dx}\Big(a^x\Big)=\dfrac{d}{dx}\Big(e^{x\ln a}\Big)=e^{x\ln a}\ln a=a^x\ln a.\)

Fomu ya ushirikiano sambamba ifuatavyo mara moja.

Derivatives na Integrals Kuhusisha Mkuu Kielelezo Kazi

Basi\(a>0.\) basi,

\[\dfrac{d}{dx}\Big(a^x\Big)=a^x \ln a \nonumber \]

na

\[∫a^x\,dx=\dfrac{1}{\ln a}a^x+C. \nonumber \]

Ikiwa\(a≠1\), basi kazi\(a^x\) ni moja kwa moja na ina inverse iliyoelezwa vizuri. Inverse yake inaashiria na\(\log_a x\). Kisha,

\( y=\log_a x\)kama na tu kama\(x=a^y.\)

Kumbuka kuwa kazi za jumla za logarithm zinaweza kuandikwa kulingana na logarithm ya asili. Basi\(y=\log_a x.\) basi,\(x=a^y\). Kuchukua logarithm ya asili ya pande zote mbili za equation hii ya pili, tunapata

\ [kuanza {align*}\ n x &=\ ln (a ^ y)\\ [5pt]
\ n x&=y\ n\\ [5pt]
y&=\ drac {\ ln x} {\ ln a}\\ [5pt]
\ log_a x&=\ dfrac {\ ln x} {\ ln a}. \ mwisho {align*}\]

Kwa hiyo, tunaona kwamba kazi zote za logarithmic ni mara nyingi za kila mmoja. Kisha, tunatumia formula hii ili kupata fomu ya kutofautisha kwa logarithm na msingi\(a\). Tena, basi\(y=\log_a x\). Kisha,

\ [kuanza {align*}\ dfrac {ddrac} {dx} &=\ dfrac {d} {dx}\ Big (\ log_a x\ Big)\\ [5pt]
&=\ dfrac {d} {dfrac}\ kushoto (\ dfrac {\ ln x} {\ ln a}\ haki)\\ [5pt]
& =(\ dfrac c {1} {\ ln a})\ dfrac {d} {dx}\ Big (\ n x\ Big)\\ [5pt]
&=\ dfrac {1} {\ ln}}\ dfrac {1} {x} =\ dfrac {1} {x\ ln a}\ mwisho {align*}\]

Derivatives ya Kazi za jumla za Logar

Basi\(a>0.\) basi,

\[\dfrac{d}{dx}\Big(\log_a x\Big)=\dfrac{1}{x\ln a}. \nonumber \]

Mfano\(\PageIndex{6}\): Calculating Derivatives of General Exponential and Logarithm Functions

Tathmini derivatives zifuatazo:

1. \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)\)
2. \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)\)

Suluhisho: Tunahitaji kutumia utawala wa mnyororo kama inavyohitajika.

1. \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t}⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t+t^2}\Big)=2^{2t+t^2}\ln (2)(2+2t)\)
2. \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)=\dfrac{1}{(7x^2+4)(\ln 8)}(14x)\)

Zoezi\(\PageIndex{6}\)

Tathmini derivatives zifuatazo:

1. \(\dfrac{d}{dt}\Big(4^{t^4}\Big)\)
2. \(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)\)

Kidokezo

Tumia fomu na utumie utawala wa mnyororo kama inavyohitajika.

Jibu

a.\(\dfrac{d}{dt}\Big(4^{t^4}\Big)=4^{t^4}(\ln 4)(4t^3)\)

b.\(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)=\dfrac{x}{(\ln 3)(x^2+1)}\)

Mfano\(\PageIndex{7}\): Integrating General Exponential Functions

Tathmini muhimu yafuatayo:\(\displaystyle ∫\dfrac{3}{2^{3x}}\,dx.\)

Suluhisho

Tumia\(u-substitution\) na uache\(u=−3x\). Kisha\(du=−3\,dx\) na tuna

\[ ∫\dfrac{3}{2^{3x}}\,dx=∫3⋅2^{−3x}\,dx=−∫2^u\,du=−\dfrac{1}{\ln 2}2^u+C=−\dfrac{1}{\ln 2}2^{−3x}+C.\nonumber \]

Zoezi\(\PageIndex{7}\)

Tathmini muhimu yafuatayo:\(\displaystyle ∫x^2 2^{x^3}\,dx.\)

Kidokezo

Tumia mali ya kazi za kielelezo na u-badala

Jibu

\(\displaystyle ∫x^2 2^{x^3}\,dx=\dfrac{1}{3\ln 2}2^{x^3}+C\)

Dhana muhimu

• Matibabu ya awali ya logarithms na kazi za kielelezo hazikufafanua kazi kwa usahihi na rasmi. Sehemu hii yanaendelea dhana kwa njia ya hesabu kali.
• Jiwe la msingi la maendeleo ni ufafanuzi wa logarithm ya asili kwa suala la muhimu.
• Kazi hiyo\(e^x\) inafafanuliwa kama inverse ya logarithm ya asili. Kazi ya jumla ya ufafanuzi hufafanuliwa kwa suala la\(e^x\), na kazi zinazofanana za inverse ni logarithms ya jumla.
• Mali inayojulikana ya logarithms na exponents bado wanashikilia katika muktadha huu mkali zaidi.

Mlinganyo muhimu

• Kazi ya logarithm ya asili
• \(\displaystyle \ln x=∫^x_1\dfrac{1}{t}\,dt\)
• Kazi ya kielelezo\(y=e^x\)
• \(\ln y=\ln (e^x)=x\)