6.5: Matumizi ya kimwili ya Ushirikiano
- Page ID
- 178254
- Kuamua wingi wa kitu kimoja cha dimensional kutoka kazi yake ya wiani wa mstari.
- Kuamua wingi wa kitu cha mviringo mbili-dimensional kutoka kazi yake ya wiani wa radial.
- Tumia kazi iliyofanywa na nguvu ya kutofautiana inayofanya kando ya mstari.
- Tumia kazi iliyofanywa kwa kusukumia kioevu kutoka urefu mmoja hadi mwingine.
- Pata nguvu ya hydrostatic dhidi ya sahani iliyojaa wima.
Katika sehemu hii, sisi kuchunguza baadhi ya maombi ya kimwili ya ushirikiano. Hebu tuanze na kuangalia kuhesabu wingi kutoka kwa kazi ya wiani. Kisha tunageuka mawazo yetu kufanya kazi, na kufunga sehemu na utafiti wa nguvu ya hydrostatic.
Misa na Wiani
Tunaweza kutumia ushirikiano kuendeleza formula kwa ajili ya kuhesabu molekuli kulingana na kazi wiani. Kwanza tunazingatia fimbo nyembamba au waya. Orient fimbo hivyo inafanana na\(x\) -axis, na mwisho wa kushoto wa fimbo\(x=a\) na mwisho wa fimbo katika\(x=b\) (Kielelezo\(\PageIndex{1}\)). Kumbuka kwamba ingawa tunaonyesha fimbo na unene fulani katika takwimu, kwa madhumuni ya hisabati tunadhani fimbo ni nyembamba ya kutosha kutibiwa kama kitu kimoja.
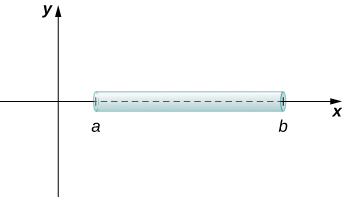
Ikiwa fimbo ina wiani wa mara kwa mara\(ρ\), iliyotolewa kwa suala la wingi kwa urefu wa kitengo, basi wingi wa fimbo ni bidhaa tu ya wiani na urefu wa fimbo:\((b−a)ρ\). Ikiwa wiani wa fimbo sio mara kwa mara, hata hivyo, tatizo linakuwa changamoto kidogo zaidi. Wakati wiani wa fimbo inatofautiana kutoka hatua kwa hatua, tunatumia kazi ya wiani wa mstari\(ρ(x)\), ili kuonyesha wiani wa fimbo wakati wowote,\(x\). Hebu\(ρ(x)\) kuwa integrable linear wiani kazi. Sasa, kwa\(P={x_i}\) kuwa\(i=0,1,2,…,n\) hebu iwe sehemu ya kawaida ya muda\([a,b]\), na kwa\(i=1,2,…,n\) kuchagua hatua ya kiholela\(x^∗_i∈[x_{i−1},x_i]\). Kielelezo\(\PageIndex{2}\) kinaonyesha sehemu ya mwakilishi wa fimbo.
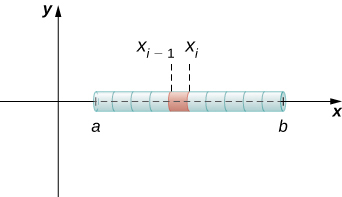
Masi\(m_i\) ya sehemu ya fimbo kutoka\(x_{i−1}\) hadi\(x_i\) inakadiriwa na
\[ \begin{align*} m_i ≈ρ(x^∗_i)(x_i−x_{i−1}) \\[4pt] =ρ(x^∗_i)Δx. \end{align*} \nonumber \]
Kuongeza raia wa makundi yote inatupa makadirio ya wingi wa fimbo nzima:
\[ \begin{align*} m =\sum_{i=1}^nm_i \\[4pt] ≈\sum_{i=1}^nρ(x^∗_i)Δx. \end{align*} \nonumber \]
Hii ni jumla Riemann. Kuchukua kikomo kama\(n→∞\), sisi kupata kujieleza kwa wingi halisi ya fimbo:
\[ \begin{align*} m =\lim_{n→∞}\sum_{i=1}^nρ(x^∗_i)Δx \\[4pt] =\int ^b_aρ(x)dx. \end{align*} \nonumber \]
Tunasema matokeo haya katika theorem ifuatayo.
Kutokana na fimbo nyembamba iliyoelekezwa kando ya\(x\) -axis juu ya muda\([a,b]\), hebu\(ρ(x)\) ueleze kazi ya wiani wa mstari kutoa wiani wa fimbo kwa hatua\(x\) katika kipindi. Kisha wingi wa fimbo hutolewa na
\[m=\int ^b_aρ(x)dx. \label{density1} \]
Tunatumia theorem hii katika mfano unaofuata.
Fikiria fimbo nyembamba iliyoelekezwa kwenye\(x\) -axis juu ya muda\([π/2,π]\). Ikiwa wiani wa fimbo hutolewa na\(ρ(x)=\sin x\), ni kiasi gani cha fimbo?
Suluhisho
Kutumia Equation\ ref {density1} moja kwa moja, tuna
\[ \begin{align*} m =\int ^b_aρ(x)dx \nonumber \\[4pt] = \int ^π_{π/2}\sin x \,dx \nonumber \\[4pt] = −\cos x \Big|^π_{π/2} \nonumber \\[4pt] = 1. \nonumber \end{align*}\]
Fikiria fimbo nyembamba iliyoelekezwa kwenye\(x\) -axis juu ya muda\([1,3]\). Ikiwa wiani wa fimbo hutolewa na\(ρ(x)=2x^2+3,\) nini umati wa fimbo?
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Suluhisho
-
\(70/3\)
Sasa tunapanua dhana hii ili kupata wingi wa disk mbili-dimensional ya radius\(r\). Kama ilivyo kwa fimbo tuliyoangalia katika kesi moja-dimensional, hapa tunadhani disk ni nyembamba ya kutosha kwamba, kwa madhumuni ya hisabati, tunaweza kutibu kama kitu mbili-dimensional. Tunadhani wiani hutolewa kwa suala la wingi kwa eneo la kitengo (inayoitwa wiani wa eneo), na zaidi kudhani wiani hutofautiana tu kwenye radius ya disk (inayoitwa wiani wa radial). Sisi kuelekeza disk katika\(xy-plane\), na kituo cha asili. Kisha, wiani wa disk unaweza kutibiwa kama kazi ya\(x\), iliyoashiria\(ρ(x)\). Sisi kudhani\(ρ(x)\) ni integrable. Kwa sababu wiani ni kazi ya\(x\), sisi kugawanya muda kutoka\([0,r]\) pamoja\(x\) -axis. Kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) iwe sehemu ya kawaida ya muda\([0,r]\), na kwa\(i=1,2,…,n\), chagua hatua ya kiholela\(x^∗_i∈[x_{i−1},x_i]\). Sasa, tumia kipengee ili kuvunja diski ndani ya washers nyembamba (mbili-dimensional). Disk na washer mwakilishi huonyeshwa katika takwimu zifuatazo.
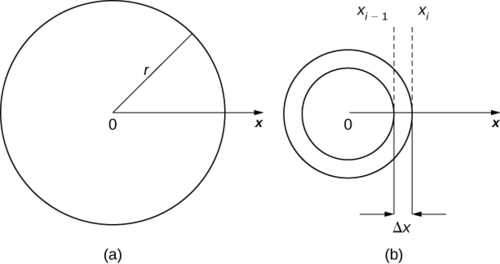
Sasa tunakaribia wiani na eneo la washer ili kuhesabu molekuli takriban,\(m_i\). Kumbuka kuwa eneo la washer linatolewa na
\[ \begin{align*} A_i =π(x_i)^2−π(x_{i−1})^2 \\[4pt] =π[x^2_i−x^2_{i−1}] \\[4pt] =π(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =π(x_i+x_{i−1})Δx. \end{align*}\]
Unaweza kukumbuka kwamba tulikuwa na usemi sawa na hii wakati tulikuwa kompyuta kiasi na shells. Kama tulivyofanya huko, tunatumia\(x^∗_i≈(x_i+x_{i−1})/2\) takriban wastani wa radius ya washer. Tunapata
\[A_i=π(x_i+x_{i−1})Δx≈2πx^∗_iΔx. \nonumber \]
\(ρ(x^∗_i)\)Kutumia takriban wiani wa washer, tunakaribia wingi wa washer
\[m_i≈2πx^∗_iρ(x^∗_i)Δx. \nonumber \]
Kuongeza raia wa washers, tunaona umati\(m\) wa disk nzima inakadiriwa na
\[m=\sum_{i=1}^nm_i≈\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx. \nonumber \]
Sisi tena kutambua hii kama jumla Riemann, na kuchukua kikomo kama\(n→∞.\) Hii inatupa
\[ \begin{align*} m =\lim_{n→∞}\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx \\[4pt] =\int ^r_02πxρ(x)dx. \end{align*}\]
Sisi muhtasari matokeo haya katika theorem zifuatazo.
Hebu\(ρ(x)\) kuwa kazi integrable inayowakilisha wiani radial ya disk ya radius\(r\). Kisha wingi wa disk hutolewa na
\[m=\int ^r_02πxρ(x)dx. \label{massEq1} \]
Hebu\(ρ(x)=\sqrt{x}\) kuwakilisha wiani wa radial wa disk. Tumia wingi wa disk ya radius 4.
Suluhisho
Kutumia Equation\ ref {Masseq1}, tunapata
\[ \begin{align*} m =\int ^r_02πxρ(x)dx \nonumber \\[4pt] =\int ^4_02πx\sqrt{x}dx=2π\int ^4_0x^{3/2}dx \nonumber \\[4pt] =2π\dfrac{2}{5}x^{5/2}∣^4_0=\dfrac{4π}{5}[32] \nonumber \\[4pt] =\dfrac{128π}{5}.\nonumber \end{align*}\]
Hebu\(ρ(x)=3x+2\) kuwakilisha wiani wa radial wa disk. Tumia wingi wa disk ya radius 2.
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Suluhisho
-
\(24π\)
Kazi Imefanywa na Nguvu
Sasa tunazingatia kazi. Katika fizikia, kazi inahusiana na nguvu, ambayo mara nyingi intuitively hufafanuliwa kama kushinikiza au kuvuta kitu. Wakati nguvu hatua kitu, tunasema nguvu gani kazi juu ya kitu. Kwa maneno mengine, kazi inaweza kufikiriwa kama kiasi cha nishati inachukua kusonga kitu. Kulingana na fizikia, tunapokuwa na nguvu ya mara kwa mara, kazi inaweza kuelezwa kama bidhaa ya nguvu na umbali.
Katika mfumo wa Kiingereza, kitengo cha nguvu ni pound na kitengo cha umbali ni mguu, hivyo kazi hutolewa kwa paundi za miguu. Katika mfumo wa metri, kilo na mita hutumiwa. Newton moja ni nguvu inayohitajika ili kuharakisha\(1\) kilo ya molekuli kwa kiwango cha\(1\) m/sec 2. Hivyo, kitengo cha kawaida cha kazi ni mita ya newton. Kitengo hiki kinaitwa pia joule. Wote hufafanuliwa kama kilo mara mita za mraba zaidi ya sekunde, mraba.\((kg⋅m^2/s^2).\)
Tunapokuwa na nguvu ya mara kwa mara, mambo ni rahisi sana. Ni nadra, hata hivyo, kwa nguvu kuwa mara kwa mara. Kazi iliyofanywa ili kuimarisha (au kupanua) chemchemi, kwa mfano, inatofautiana kulingana na umbali gani spring tayari imesisitizwa (au imetambulishwa). Tunaangalia chemchemi kwa undani zaidi baadaye katika sehemu hii.
Tuseme tuna nguvu variable\(F(x)\) kwamba hatua kitu katika mwelekeo chanya pamoja\(x\) mhimili -kutoka hatua\(a\) kwa uhakika\(b\). Ili kuhesabu kazi iliyofanywa, tunagawanya muda\([a,b]\) na kukadiria kazi iliyofanywa juu ya kila subinterval. Kwa hiyo, kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) iwe sehemu ya kawaida ya muda\([a,b]\), na kwa\(i=1,2,…,n\), chagua hatua ya kiholela\(x^∗_i∈[x_{i−1},x_i]\). Ili kuhesabu kazi iliyofanywa ili kusonga kitu kutoka hatua\(x_{i−1}\) kwa hatua\(x_i\), tunadhani nguvu ni takribani mara kwa mara juu ya muda, na kutumia\(F(x^∗_i)\) kwa takriban nguvu. Kazi iliyofanywa zaidi ya muda\([x_{i−1},x_i]\), basi, inatolewa na
\[W_i≈F(x^∗_i)(x_{i}−x_{i−1})=F(x^∗_i)Δx. \nonumber \]
Kwa hiyo, kazi iliyofanyika zaidi ya muda\([a,b]\) ni takriban
\[W=\sum_{i=1}^nW_i≈\sum_{i=1}^nF(x^∗_i)Δx. \nonumber \]
Kuchukua kikomo cha maneno haya kama\(n→∞\) inatupa thamani halisi ya kazi:
\[ \begin{align*} W =\lim_{n→∞}\sum_{i=1}^nF(x^∗_i)Δx \\[4pt] =\int ^b_aF(x)dx. \end{align*}\]
Hivyo, tunaweza kufafanua kazi kama ifuatavyo.
Ikiwa nguvu ya kutofautiana\(F(x)\) husababisha kitu katika mwelekeo mzuri kando ya\(x\) -axis kutoka hatua\(a\) hadi hatua\(b\), basi kazi iliyofanywa kwenye kitu ni
\[W=\int ^b_aF(x)dx. \label{work} \]
Kumbuka kwamba ikiwa\(F\) ni mara kwa mara, muhimu hutathmini\(F⋅(b−a)=F⋅d,\) ambayo ni formula tuliyosema mwanzoni mwa sehemu hii.
Sasa hebu tuangalie mfano maalum wa kazi iliyofanywa ili kuimarisha au kupanua spring. Fikiria kizuizi kilichounganishwa na chemchemi ya usawa. Kizuizi kinaendelea na kurudi kama chemchemi inavyoweka na kuimarisha. Ingawa katika ulimwengu wa kweli tutakuwa na akaunti kwa nguvu ya msuguano kati ya kuzuia na uso ambayo ni kupumzika, sisi kupuuza msuguano hapa na kudhani block ni kupumzika juu ya uso frictionless. Wakati chemchemi iko katika urefu wake wa asili (wakati wa kupumzika), mfumo unasemekana kuwa katika usawa. Katika hali hii, chemchemi haipatikani wala imesisitizwa, na katika nafasi hii ya usawa block haina hoja mpaka nguvu fulani itaanzishwa. Tunaelekeza mfumo huo\(x=0\) unaofanana na msimamo wa usawa (Kielelezo\(\PageIndex{4}\)).
Kwa mujibu wa sheria ya Hooke, nguvu inayotakiwa kuimarisha au kunyoosha chemchemi kutoka nafasi ya usawa hutolewa na\(F(x)=kx\), kwa mara kwa mara\(k\). Thamani ya k inategemea sifa za kimwili za chemchemi. Mara kwa mara\(k\) huitwa mara kwa mara ya spring na daima ni chanya. Tunaweza kutumia habari hii kuhesabu kazi iliyofanywa ili kuimarisha au kupanua chemchemi, kama inavyoonekana katika mfano unaofuata.
Tuseme inachukua nguvu ya\(10\) N (katika mwelekeo hasi) ili kuimarisha\(0.2\) m spring kutoka nafasi ya usawa. Ni kazi gani inayofanywa ili kunyoosha\(0.5\) m ya spring kutoka nafasi ya usawa?
Suluhisho
Kwanza kupata spring mara kwa mara,\(k\). Wakati\(x=−0.2\), tunajua\(F(x)=−10,\) hivyo
\[ \begin{align*} F(x) =kx \\[4pt] −10 =k(−0.2) \\[4pt] k =50 \end{align*}\]
na\(F(x)=50x.\) Kisha, kufanya mahesabu ya kazi, sisi kuunganisha kazi nguvu, kupata
\[\begin{align*} W = \int ^b_aF(x)dx \\[4pt] =\int ^{0.5}_050 x \,dx \\[4pt] =\left. 25x^2 \right|^{0.5}_0 \\[4pt] =6.25. \end{align*}\]
Kazi iliyofanywa ili kunyoosha chemchemi ni\(6.25\) J.
Tuseme inachukua nguvu ya\(8\) lb kunyoosha spring\(6\) katika. kutoka nafasi ya usawa. Ni kazi gani inayofanywa ili kunyoosha\(1\) ft ya spring kutoka nafasi ya usawa?
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita. Kuwa makini na vitengo.
- Suluhisho
-
\(8\)ft-lb
Kazi Imefanyika katika Pumping
Fikiria kazi iliyofanywa ili kupiga maji (au kioevu kingine) nje ya tangi. Matatizo ya kusubu ni ngumu zaidi kuliko matatizo ya spring kwa sababu mahesabu mengi hutegemea sura na ukubwa wa tank. Aidha, badala ya kuwa na wasiwasi juu ya kazi iliyofanywa ili kuhamisha molekuli moja, tunaangalia kazi iliyofanywa ili kuhamisha kiasi cha maji, na inachukua kazi zaidi ya kuhamisha maji kutoka chini ya tangi kuliko inavyofanya kuhamisha maji kutoka juu ya tank.
Tunachunguza mchakato katika mazingira ya tank ya cylindrical, kisha angalia mifano michache kwa kutumia mizinga ya maumbo tofauti. Fikiria tank cylindrical ya radius\(4\)\(10\) m na urefu m ni kujazwa kwa kina cha m 8 ni kazi gani inachukua kusubu maji yote juu ya makali ya juu ya tank?
Jambo la kwanza tunalohitaji kufanya ni kufafanua sura ya kumbukumbu. Tunaruhusu\(x\) kuwakilisha umbali wa wima chini ya juu ya tank. Hiyo ni, tunaelekeza\(x\) -axis vertically, na asili ya juu ya tank na mwelekeo wa chini kuwa chanya (Kielelezo\(\PageIndex{5}\)).
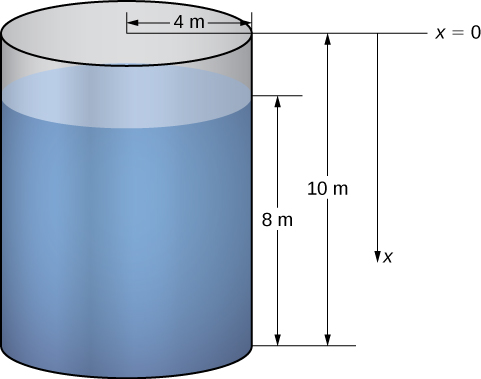
Kutumia mfumo huu wa kuratibu, maji yanaendelea kutoka\(x=2\) hadi\(x=10\). Kwa hiyo, tunagawanya muda\([2,10]\) na kuangalia kazi inayohitajika kuinua kila “safu” ya maji. Kwa hiyo, kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) iwe sehemu ya kawaida ya muda\([2,10]\), na kwa\(i=1,2,…,n\), chagua hatua ya kiholela\(x^∗_i∈[x_{i−1},x_i]\). Kielelezo\(\PageIndex{6}\) kinaonyesha safu ya mwakilishi.
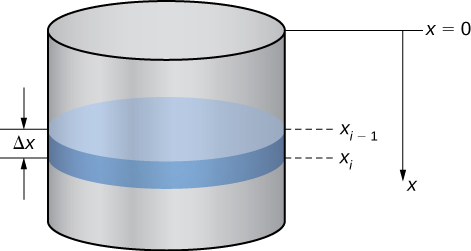
Katika matatizo ya kusukumia, nguvu inayotakiwa kuinua maji hadi juu ya tangi ni nguvu inayotakiwa kushinda mvuto, hivyo ni sawa na uzito wa maji. Kutokana na kwamba wiani wa uzito wa maji ni\(9800 \, \text{N/m}^3\)\(62.4\,\text{lb/ft}^3\), au, kuhesabu kiasi cha kila safu inatupa uzito. Katika kesi hiyo, tuna
\[V=π(4)^2Δx=16πΔx. \nonumber \]
Kisha, nguvu zinahitajika kuinua kila safu ni
\[F=9800⋅16πΔx=156,800πΔx. \nonumber \]
Kumbuka kuwa hatua hii inakuwa ngumu zaidi ikiwa tuna tank isiyo na cylindrical. Tunaangalia tank isiyo na cylindrical katika mfano unaofuata.
Pia tunahitaji kujua umbali wa maji lazima iinuliwe. Kulingana na uchaguzi wetu wa mifumo ya kuratibu, tunaweza kutumia\(x^∗_i\) kama makadirio ya umbali safu lazima iinuliwe. Kisha kazi ya kuinua\(i^{\text{th}}\) safu ya maji\(W_i\) ni takriban
\[W_i≈156,800πx^∗_iΔx. \nonumber \]
Kuongeza kazi kwa kila safu, tunaona kazi ya takriban ya kufuta tank hutolewa na
\[ \begin{align*} W =\sum_{i=1}^nW_i \\[4pt] ≈\sum_{i=1}^n156,800πx^∗_iΔx.\end{align*}\]
Hii ni jumla Riemann, hivyo kuchukua kikomo kama\(n→∞,\) sisi kupata
\[ \begin{align*} W =\lim_{n→∞}\sum^n_{i=1}156,800πx^∗_iΔx \\[4pt] = 156,800π\int ^{10}_2xdx \\[4pt] =156,800π \left( \dfrac{x^2}{2}\right)\bigg|^{10}_2=7,526,400π≈23,644,883. \end{align*}\]
Kazi inayotakiwa kufuta tank ni takriban 23,650,000 J.
Kwa matatizo ya kusukumia, mahesabu hutofautiana kulingana na sura ya tank au chombo. Mkakati wafuatayo wa kutatua matatizo huweka mchakato wa hatua kwa hatua wa kutatua matatizo ya kusukumia.
- Mchoro picha ya tank na uchague sura sahihi ya kumbukumbu.
- Tumia kiasi cha safu ya mwakilishi wa maji.
- Panua kiasi kwa wiani wa uzito wa maji ili kupata nguvu.
- Tumia umbali safu ya maji inapaswa kuinuliwa.
- Kuzidisha nguvu na umbali ili kupata makadirio ya kazi inahitajika kuinua safu ya maji.
- Jumuisha kazi inayohitajika ili kuinua tabaka zote. Maneno haya ni makadirio ya kazi inayotakiwa kupiga kiasi cha maji kilichohitajika, na ni kwa namna ya jumla ya Riemann.
- Chukua kikomo kama\(n→∞\) na tathmini muhimu inayosababisha kupata kazi halisi inayohitajika ili kupiga kiasi cha maji kilichohitajika.
Sasa tunatumia mkakati huu wa kutatua matatizo kwa mfano na tank isiyo na cylindrical.
Tumia tank katika sura ya koni iliyoingizwa, na urefu wa\(12\) ft na msingi wa radius\(4\) ft. Tangi imejaa kuanza na, na maji hupigwa juu ya makali ya juu ya tank mpaka urefu wa maji iliyobaki katika tangi ni\(4\) ft. Ni kazi gani inahitajika kupiga kiasi hicho cha maji?
Suluhisho
Tangi inaonyeshwa kwenye Kielelezo\(\PageIndex{7}\). Kama tulivyofanya katika mfano na tank ya cylindrical, tunaelekeza\(x\) -axis vertically, na asili ya juu ya tank na mwelekeo wa chini kuwa chanya (hatua ya 1).
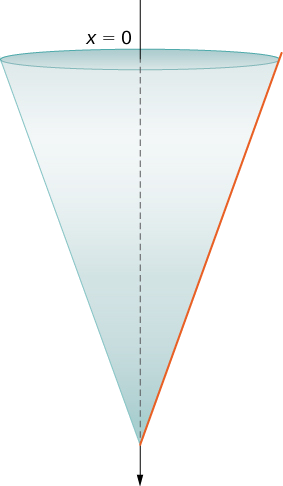
Tangi huanza kamili na kuishia na\(4\) ft ya maji kushoto, kwa hiyo, kulingana na sura yetu iliyochaguliwa ya kumbukumbu, tunahitaji kugawanya muda\([0,8]\). Kisha, kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) iwe sehemu ya kawaida ya muda\([0,8]\), na kwa\(i=1,2,…,n\), chagua hatua ya kiholela\(x^∗_i∈[x_{i−1},x_i]\). Tunaweza takriban kiasi cha safu kwa kutumia diski, kisha tumia pembetatu sawa ili kupata radius ya disk (Kielelezo\(\PageIndex{8}\)).
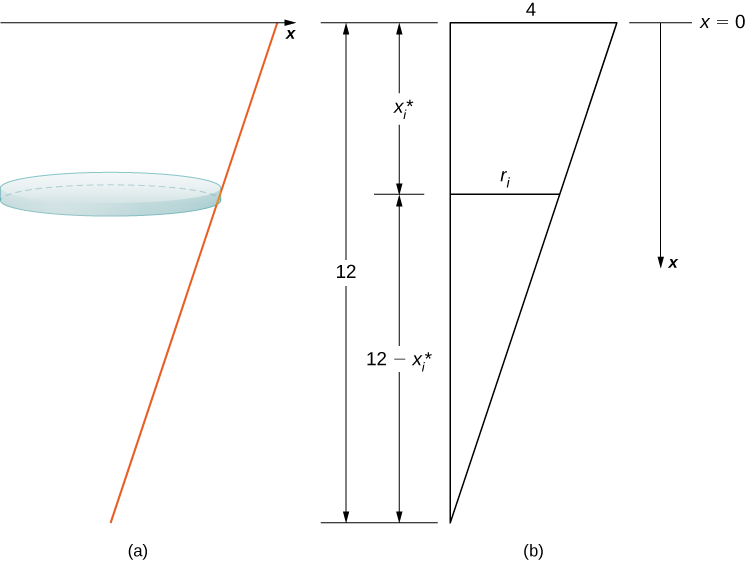
Kutoka kwa mali ya pembetatu sawa, tuna
\[ \begin{align*} \dfrac{r_i}{12−x^∗_i} =\dfrac{4}{12} \tag{step 1} =\dfrac{1}{3} \\[4pt] 3r_i =12−x^∗_i \\[4pt] r_i =\dfrac{12−x^∗_i}{3} \\[4pt] =4−\dfrac{x^∗_i}{3}. \end{align*} \]
Kisha kiasi cha disk ni
\[V_i=π \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 2} \]
Uzito wiani wa maji ni\(62.4\) lb/ft 3, hivyo nguvu inahitajika kuinua kila safu ni takriban
\[F_i≈62.4π\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx \tag{step 3} \]
Kulingana na mchoro, umbali wa maji lazima iinuliwe ni takriban\(x^∗_i\) miguu (hatua ya 4), hivyo kazi ya takriban inahitajika kuinua safu ni
\[W_i≈62.4πx^∗_i\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 5} \]
Kuhitimisha kazi inayohitajika kuinua tabaka zote, tunapata thamani ya takriban ya kazi ya jumla:
\[W=\sum_{i=1}^nW_i≈\sum_{i=1}^n62.4πx^∗_i \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 6} \]
Kuchukua kikomo kama\(n→∞,\) sisi kupata
\[ \begin{align*} W =\lim_{n→∞}\sum^n_{i=1}62.4πx^∗_i(4−\dfrac{x^∗_i}{3})^2Δx \\[4pt] = \int ^8_062.4πx \left(4−\dfrac{x}{3}\right)^2dx \\[4pt] = 62.4π\int ^8_0x \left(16−\dfrac{8x}{3}+\dfrac{x^2}{9}\right)\,dx=62.4π\int ^8_0 \left(16x−\dfrac{8x^2}{3}+\dfrac{x^3}{9}\right)\,dx \\[4pt] =62.4π\left[8x^2−\dfrac{8x^3}{9}+\dfrac{x^4}{36}\right]\bigg|^8_0=10,649.6π≈33,456.7. \end{align*}\]
Inachukua takriban\(33,450\) ft-lb ya kazi ili tupu tank kwa kiwango cha taka.
Tangi iko katika sura ya koni iliyoingizwa, na urefu wa\(10\) ft na msingi wa radius 6 ft. Tangi imejazwa kwa kina cha futi 8 kuanza na, na maji hupigwa juu ya makali ya juu ya tangi mpaka futi 3 za maji kubaki katika tangi. Ni kazi gani inahitajika kupiga kiasi hicho cha maji?
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Suluhisho
-
Takriban\(43,255.2\) ft-lb
Nguvu ya maji na Shinikizo
Katika sehemu hii ya mwisho, tunaangalia nguvu na shinikizo lililowekwa kwenye kitu kilichoingia kwenye kioevu. Katika mfumo wa Kiingereza, nguvu inapimwa kwa paundi. Katika mfumo wa metri, hupimwa katika newtons. Shinikizo ni nguvu kwa kila eneo la kitengo, hivyo katika mfumo wa Kiingereza tuna paundi kwa mguu wa mraba (au, labda zaidi, paundi kwa inchi ya mraba, iliyoashiria psi). Katika mfumo wa metri tuna newtons kwa kila mita ya mraba, pia huitwa pascals.
Hebu tuanze na kesi rahisi ya sahani ya eneo\(A\) limejaa usawa katika maji kwa kina s (Kielelezo\(\PageIndex{9}\)). Kisha, nguvu iliyotumiwa kwenye sahani ni uzito wa maji juu yake, ambayo hutolewa na\(F=ρAs\), wapi\(ρ\) wiani wa uzito wa maji (uzito kwa kiasi cha kitengo). Ili kupata shinikizo la hydrostatic -yaani, shinikizo linalotumiwa na maji kwenye kitu kilichojawa-tunagawanya nguvu na eneo hilo. Hivyo shinikizo ni\(p=F/A=ρs\).
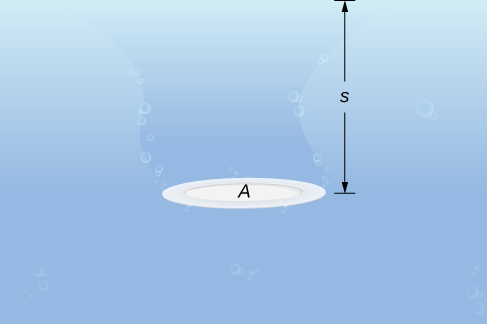
Kwa kanuni ya Pascal, shinikizo kwa kina kilichopewa ni sawa kwa pande zote, kwa hiyo haijalishi kama sahani imefungwa kwa usawa au kwa wima. Kwa hiyo, kwa muda mrefu kama tunajua kina, tunajua shinikizo. Tunaweza kutumia kanuni ya Pascal ili kupata nguvu iliyotumiwa kwenye nyuso, kama vile mabwawa, ambayo yanaelekezwa kwa wima. Hatuwezi kutumia formula\(F=ρAs\) moja kwa moja, kwa sababu kina hutofautiana kutoka hatua hadi hatua kwenye uso unaoelekezwa kwa wima. Kwa hiyo, kama tulivyofanya mara nyingi kabla, tunaunda kizuizi, jumla ya Riemann, na hatimaye, muhimu ya kuhesabu nguvu.
Tuseme sahani nyembamba imejaa ndani ya maji. Tunachagua sura yetu ya kumbukumbu kama vile\(x\) -axis inaelekezwa kwa wima, na mwelekeo wa kushuka kuwa chanya, na uhakika\(x=0\) unaohusiana na hatua ya kumbukumbu ya mantiki. Hebu\(s(x)\) kuashiria kina katika hatua x Kumbuka sisi mara nyingi basi\(x=0\) yanahusiana na uso wa maji. Katika kesi hii, kina wakati wowote hutolewa tu na\(s(x)=x\). Hata hivyo, wakati mwingine tunaweza kutaka kuchagua hatua tofauti ya kumbukumbu\(x=0\), kwa hiyo tunaendelea na maendeleo katika kesi ya jumla zaidi. Mwisho,\(w(x)\) hebu ueleze upana wa sahani wakati huo\(x\).
Tuseme makali ya juu ya sahani ni katika hatua\(x=a\) na makali ya chini ya sahani ni katika hatua\(x=b\). Kisha, kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) iwe sehemu ya kawaida ya muda\([a,b]\), na kwa\(i=1,2,…,n\), chagua hatua ya kiholela\(x^∗_i∈[x_{i−1},x_i]\). Ugavi hugawanya sahani katika vipande kadhaa nyembamba, vya mstatili (Kielelezo\(\PageIndex{10}\)).
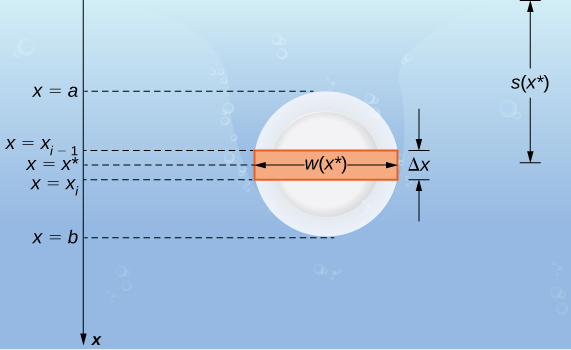
Hebu sasa tuchunguze nguvu kwenye mstari wa mwakilishi. Kama strip ni nyembamba ya kutosha, tunaweza kutibu kama ni katika kina mara kwa mara,\(s(x^∗_i)\). Sisi basi
\[F_i=ρAs=ρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber \]
Kuongeza nguvu, tunapata makadirio ya nguvu kwenye sahani:
\[F≈\sum_{i=1}^nF_i=\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber \]
Hii ni jumla ya Riemann, hivyo kuchukua kikomo inatupa nguvu halisi. Tunapata
\[F=\lim_{n→∞}\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i)=\int ^b_aρw(x)s(x)dx. \label{eqHydrostatic} \]
Kutathmini muhimu hii inatupa nguvu kwenye sahani. Sisi muhtasari huu katika mkakati zifuatazo kutatua matatizo.
- Mchoro picha na uchague sura sahihi ya kumbukumbu. (Kumbuka kwamba kama sisi kuchagua sura ya kumbukumbu zaidi ya moja kutumika mapema, tunaweza kuwa na kurekebisha Equation\ ref {EqHydrostatic} ipasavyo.)
- Kuamua kina na upana kazi,\(s(x)\) na\(w(x).\)
- Kuamua uzito wiani wa kioevu chochote unachofanya kazi. Uzito wiani wa maji ni\(62.4 \,\text{lb/ft}^3\), au\(9800 \,\text{N/m}^3\).
- Tumia equation kuhesabu nguvu ya jumla.
Mto wa maji 15 ft mrefu una mwisho umbo kama pembetatu isosceles inverted, na msingi 8 ft na urefu 3 ft. Pata nguvu kwenye mwisho mmoja wa shimo ikiwa mto umejaa maji.
Suluhisho
Kielelezo\(\PageIndex{11}\) kinaonyesha mto na mtazamo wa kina zaidi wa mwisho mmoja.
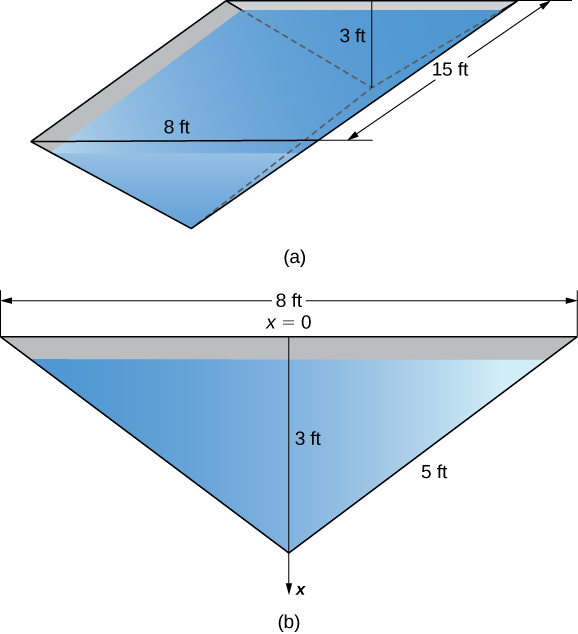
Chagua sura ya kumbukumbu na\(x\) -axis oriented wima na mwelekeo wa chini kuwa chanya. Chagua juu ya shimo kama hatua inayohusiana na\(x=0\) (hatua ya 1). Kazi ya kina, basi, ni\(s(x)=x\). Kutumia pembetatu sawa, tunaona kwamba\(w(x)=8−(8/3)x\) (hatua ya 2). Sasa, uzito wiani wa maji ni\(62.4 \,\text{lb/ft}^3\) (hatua 3), hivyo kutumia Equation\ ref {eqHydrostatic}, sisi kupata
\[ \begin{align*} F =\int ^b_aρw(x)s(x)dx \\[4pt] = \int ^3_062.4 \left(8−\dfrac{8}{3}x\right) x \,dx=62.4\int ^3_0 \left(8x−\dfrac{8}{3}x^2 \right)dx \\[4pt] = \left.62.4 \left[4x^2−\dfrac{8}{9}x^3\right]\right|^3_0=748.8. \end{align*}\]
Maji huwa na nguvu ya 748.8 lb mwishoni mwa mto (hatua ya 4).
Maji kupitia nyimbo 12 m kwa muda mrefu ina mwisho umbo kama pembetatu inverted isosceles, na msingi 6 m na urefu 4 m Kupata nguvu juu ya mwisho mmoja wa kupitia nyimbo kama mfereji ni kamili ya maji.
- Kidokezo
-
Fuata mkakati wa kutatua matatizo na mchakato kutoka kwa mfano uliopita.
- Suluhisho
-
\(156,800\)N
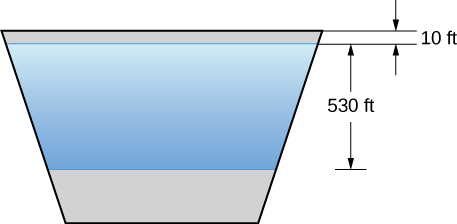
Sasa tunarudi mawazo yetu kwa Mkwawa wa Hoover, uliotajwa mwanzoni mwa sura hii. Bwawa halisi ni arched, badala ya gorofa, lakini sisi ni kwenda kufanya baadhi ya mawazo kurahisisha kutusaidia na hesabu. Tuseme uso wa Bwawa la Hoover umeumbwa kama trapezoid ya isosceles yenye msingi wa chini 750 ft, msingi wa juu 1250 ft, na urefu wa 750 ft (angalia takwimu zifuatazo).

Wakati hifadhi imejaa, kina cha juu cha Ziwa Mead ni takriban futi 530, na uso wa ziwa ni karibu 10 ft chini ya juu ya bwawa (angalia takwimu zifuatazo).
- Pata nguvu juu ya uso wa bwawa wakati hifadhi imejaa.
- Kusini magharibi mwa Marekani imekuwa inakabiliwa na ukame, na uso wa Ziwa Mead ni takriban futi 125 chini ambapo ingekuwa kama hifadhi ingekuwa imejaa. Ni nguvu gani juu ya uso wa bwawa chini ya hali hizi?
Suluhisho:
a.
Tunaanza kwa kuanzisha sura ya kumbukumbu. Kama kawaida, tunachagua kuelekeza\(x\) -axis vertically, na mwelekeo wa chini kuwa chanya. Wakati huu, hata hivyo, sisi ni kwenda basi\(x=0\) kuwakilisha juu ya bwawa, badala ya uso wa maji. Wakati hifadhi imejaa, uso wa maji ni\(10\) ft chini ya juu ya bwawa, hivyo\(s(x)=x−10\) (angalia takwimu zifuatazo).

Ili kupata kazi ya upana, tunarudi tena kwenye pembetatu sawa kama inavyoonekana kwenye takwimu hapa chini.
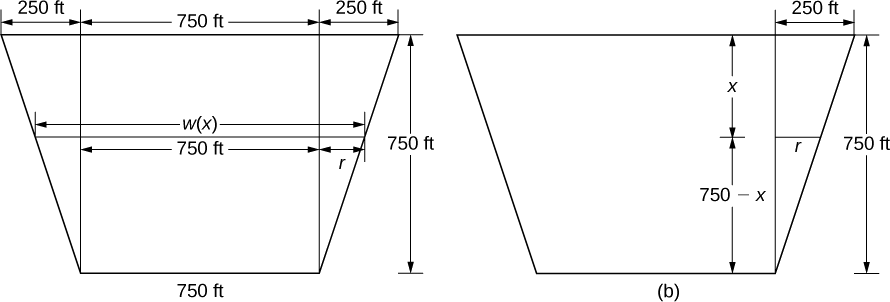
Kutoka kwenye takwimu, tunaona hiyo\(w(x)=750+2r\). Kutumia mali ya pembetatu sawa, tunapata\(r=250−(1/3)x\). Hivyo,
\[w(x)=1250−\dfrac{2}{3}x \tag{step 2} \]
Kutumia uzito wiani wa\(62.4\) lb/ft 3 (hatua 3) na kutumia Equation\ ref {EqHydrostatic}, tunapata
\ [kuanza {align*} F =\ int^b_a ρw (x) s (x)\, dx\\ [4pt]
=\ int ^ {540} _ {10} 62.4\ kushoto (1250—\ dfrac {2} {3} x\ haki) (x-10)\, dx\\ [4pt]
=62.4\ int ^ {540} _ {540} _ {10} -\ dfrac {2} {3} [x^2,185x+18750]\, dx\\ [4pt]
=-62.4\ kushoto (\ dfrac {2} {3}\ kulia)\ kushoto [\ dfrac {x^3} {3}}\ dfrac {1885x^2} {2} +18750x\ haki]\ kubwa|^ {540} _ {10} ≈ 8,832,245,000\,\ maandishi {lb} =4,416,122.5\,\ maandishi {t}. \ mwisho {align*}\]
Kumbuka mabadiliko kutoka paundi hadi tani (\(2000\)lb =\(1\) tani) (hatua ya 4). Hii inabadilisha kazi yetu ya kina,\(s(x)\), na mipaka yetu ya ushirikiano. Tuna\(s(x)=x−135\). Kikomo cha chini cha ushirikiano ni 135. Kikomo cha juu kinabakia\(540\). Kutathmini muhimu, tunapata
\ [kuanza {align*} F =\ int^b_aρw (x) s (x)\, dx\\ [4pt]
=\ int ^ {540} _ {135} 62.4\ kushoto (1250-dfrac {2} {3} x\ haki) (x-135)\, dx\\ [4pt]
=-62.4 (\ dfrac {2}} {3})\ int ^ {540} _ {135} (x-1875) (x-135)\, dx=-62.4\ kushoto (\ dfrac {2} {3}\ haki)\ int ^ {540} _ {135} (x^2,10x+253125)\, dx\\ [4pt]
=-62.4\ kushoto (\ dfrac {2} {3}\ kulia)\ kushoto [\ dfrac {x^3} {3} -1005x^2+253125x\ haki]\ kubwa|^ {540} _ {135} ≈ 5,015,230,000\,\ maandishi {lb} =2,507,615\,\ maandishi {t}. \ mwisho {align*}\]
Wakati hifadhi iko katika kiwango chake cha wastani, uso wa maji ni karibu 50 ft chini ambapo itakuwa kama hifadhi ingekuwa imejaa. Ni nguvu gani juu ya uso wa bwawa chini ya hali hizi?
- Kidokezo
-
Badilisha kazi ya kina,\(s(x),\) na mipaka ya ushirikiano.
- Suluhisho
-
Takriban 7,164,520,000 lb au 3,582,260 t
Dhana muhimu
- Matumizi kadhaa ya kimwili ya muhimu ya uhakika ni ya kawaida katika uhandisi na fizikia.
- Integrals ya uhakika inaweza kutumika kuamua wingi wa kitu ikiwa kazi yake ya wiani inajulikana.
- Kazi pia inaweza kuhesabiwa kutoka kuunganisha kazi ya nguvu, au wakati wa kukabiliana na nguvu ya mvuto, kama katika tatizo la kusukumia.
- Integrals uhakika pia inaweza kutumika kwa ajili ya mahesabu ya nguvu exerted juu ya kitu iliyoingia katika kioevu.
Mlinganyo muhimu
- Misa ya kitu kimoja
\( \displaystyle m=\int ^b_aρ(x)dx\)
- Misa ya kitu cha mviringo
\(\displaystyle m=\int ^r_02πxρ(x)dx\)
- Kazi iliyofanyika kwenye kitu
\(\displaystyle W=\int ^b_aF(x)dx\)
- Nguvu ya hydrostatic kwenye sahani
\(\displaystyle F=\int ^b_aρw(x)s(x)dx\)
faharasa
- kazi ya wiani
- kazi ya wiani inaelezea jinsi wingi unavyoshirikiwa katika kitu; inaweza kuwa wiani wa mstari, ulioonyeshwa kwa suala la wingi kwa urefu wa kitengo; wiani wa eneo, ulioonyeshwa kwa suala la wingi kwa eneo la kitengo; au wiani wa kiasi, ulioonyeshwa kwa suala la wingi kwa kiasi cha kitengo; wiani wa uzito pia hutumiwa kuelezea uzito (badala ya wingi) kwa kiasi cha kitengo
- Sheria ya Hooke
- sheria hii inasema kwamba nguvu inahitajika compress (au elongate) spring ni sawia na umbali spring imekuwa USITUMIE (au aliweka) kutoka usawa; kwa maneno mengine\(F=kx\), wapi\(k\) mara kwa mara
- shinikizo la hydrostatic
- shinikizo linalojitokeza na maji kwenye kitu kilichojaa
- kazi
- kiasi cha nishati inachukua kusonga kitu; katika fizikia, wakati nguvu ni mara kwa mara, kazi inaelezwa kama bidhaa ya nguvu na umbali


