6.4: Urefu wa Arc wa Eneo la Curve na Uso

Last updated
Save as PDF

Page ID: 178367

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Kuamua urefu wa Curve,\(y=f(x)\), kati ya pointi mbili.
Kuamua urefu wa Curve,\(x=g(y)\), kati ya pointi mbili.
Pata eneo la uso wa imara ya mapinduzi.

Katika sehemu hii, tunatumia viungo vya uhakika ili kupata urefu wa arc wa safu. Tunaweza kufikiria urefu wa safu kama umbali ungependa kusafiri kama ungekuwa kutembea kando ya njia ya Curve. Maombi mengi ya ulimwengu halisi yanahusisha urefu wa safu. Kama roketi ni ilizinduliwa pamoja njia parabolic, tunaweza kutaka kujua jinsi mbali roketi safari. Au, kama Curve kwenye ramani inawakilisha barabara, tunaweza kutaka kujua ni umbali gani tunapaswa kuendesha gari kufikia marudio yetu.

Tunaanza kwa kuhesabu safu urefu wa curves hufafanuliwa kama kazi ya\( x\), kisha sisi kuchunguza mchakato huo kwa curves hufafanuliwa kama kazi ya\( y\). (Mchakato huo ni sawa, na majukumu ya\( x\) na\( y\) kuachwa.) Mbinu tunazotumia kupata urefu wa arc zinaweza kupanuliwa ili kupata eneo la uso wa mapinduzi, na tunakaribia sehemu kwa uchunguzi wa dhana hii.

Urefu wa safu ya Curve y = f (x)

Katika maombi ya awali ya ushirikiano,\( f(x)\) tulihitaji kazi kuwa integrable, au kwa kuendelea zaidi. Hata hivyo, kwa kuhesabu urefu wa arc tuna mahitaji magumu zaidi\( f(x)\). Hapa,\( f(x)\) tunahitaji kuwa differentiable, na zaidi ya hayo tunahitaji derivative yake, kuwa\( f′(x),\) kuendelea. Kazi kama hii, ambayo ina derivatives inayoendelea, inaitwa laini. (Mali hii inakuja tena katika sura za baadaye.)

Hebu\( f(x)\) kuwa kazi laini defined juu ya\( [a,b]\). Tunataka kuhesabu urefu wa curve kutoka hatua\( (a,f(a))\) hadi hatua\( (b,f(b))\). Tunaanza kwa kutumia makundi ya mstari ili takriban urefu wa curve. Kwa\( i=0,1,2,…,n\), hebu\( P={x_i}\) kuwa sehemu ya kawaida ya\( [a,b]\). Kisha, kwa\( i=1,2,…,n\), kujenga sehemu line kutoka hatua\( (x_{i−1},f(x_{i−1}))\) kwa uhakika\( (x_i,f(x_i))\). Ingawa inaweza kuonekana kuwa mantiki kutumia makundi ya mstari wa usawa au wima, tunataka makundi yetu ya mstari kufikia karibu iwezekanavyo. Kielelezo\(\PageIndex{1}\) inaonyesha kujenga hii kwa\( n=5\).

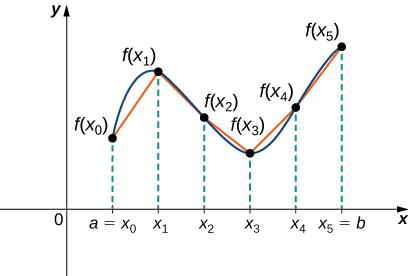
Takwimu hii ni grafu katika quadrant ya kwanza. Curve huongezeka na hupungua. Imegawanywa katika sehemu katika pointi a=xsub0, xsub1, xsub2, xsub3, xsub4, na xsub5=b Pia, kuna makundi ya mstari kati ya pointi kwenye pembe. — Kielelezo\(\PageIndex{1}\): Tunaweza takriban urefu wa curve kwa kuongeza makundi ya mstari.

Ili kutusaidia kupata urefu wa kila sehemu ya mstari, tunaangalia mabadiliko katika umbali wa wima pamoja na mabadiliko katika umbali wa usawa juu ya kila kipindi. Kwa sababu tumetumia ugawaji wa kawaida, mabadiliko katika umbali wa usawa juu ya kila kipindi hutolewa na\( Δx\). Mabadiliko katika umbali wa wima hutofautiana kutoka kwa muda hadi muda, ingawa, kwa hiyo tunatumia\( Δy_i=f(x_i)−f(x_{i−1})\) kuwakilisha mabadiliko katika umbali wa wima juu ya muda\( [x_{i−1},x_i]\), kama inavyoonekana kwenye Mchoro\(\PageIndex{2}\). Kumbuka kwamba baadhi (au yote)\( Δy_i\) inaweza kuwa hasi.

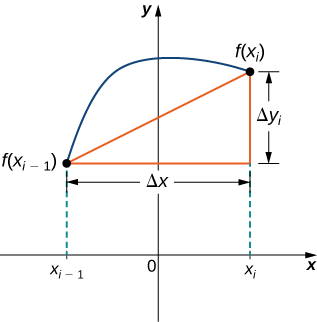
Takwimu hii ni grafu. Ni curve juu ya x-axis kuanzia katika hatua f (xsubi-1). Curve inaishia katika roboduara ya kwanza kwenye hatua f (xsubi). Kati ya pointi mbili kwenye Curve ni sehemu ya mstari. Pembetatu ya kulia inaundwa na sehemu hii ya mstari kama hypotenuse, sehemu ya usawa na delta ya urefu x, na sehemu ya mstari wa wima na delta ya urefu y. — Kielelezo\(\PageIndex{2}\): Mwakilishi line sehemu approximates Curve juu ya muda\( [x_{i−1},x_i].\)

Kwa theorem ya Pythagorean, urefu wa sehemu ya mstari ni

\[ \sqrt{(Δx)^2+(Δy_i)^2}. \nonumber \]

Tunaweza pia kuandika hii kama

\[ Δx\sqrt{1+((Δy_i)/(Δx))^2}. \nonumber \]

Sasa, kwa Theorem ya Theorem ya Thamani, kuna hatua\( x^∗_i∈[x_{i−1},x_i]\) kama hiyo\( f′(x^∗_i)=(Δy_i)/(Δx)\). Kisha urefu wa sehemu ya mstari hutolewa na

\[ Δx\sqrt{1+[f′(x^∗_i)]^2}. \nonumber \]

Kuongeza urefu wa makundi yote ya mstari, tunapata

\[\text{Arc Length} ≈\sum_{i=1}^n\sqrt{1+[f′(x^∗_i)]^2}Δx.\nonumber \]

Hii ni jumla Riemann. Kuchukua kikomo kama\( n→∞,\) tuna

\[\begin{align*} \text{Arc Length} &=\lim_{n→∞}\sum_{i=1}^n\sqrt{1+[f′(x^∗_i)]^2}Δx \\[4pt] &=∫^b_a\sqrt{1+[f′(x)]^2}dx.\end{align*}\]

Sisi muhtasari matokeo haya katika theorem zifuatazo.

Urefu wa Arc kwa\( y = f(x)\)

Hebu\( f(x)\) kuwa kazi laini juu ya muda\([a,b]\). Kisha urefu wa arc wa sehemu ya grafu ya\( f(x)\) kutoka hatua\( (a,f(a))\) hadi hatua\( (b,f(b))\) hutolewa na

\[\text{Arc Length}=∫^b_a\sqrt{1+[f′(x)]^2}\,dx. \nonumber \]

Kumbuka kwamba sisi ni kuunganisha kujieleza kuwashirikisha\( f′(x)\), hivyo tunahitaji kuwa na uhakika\( f′(x)\) ni integrable. Hii ndiyo sababu\( f(x)\) tunahitaji kuwa laini. Mfano unaofuata unaonyesha jinsi ya kutumia theorem.

Mfano\( \PageIndex{1}\): Calculating the Arc Length of a Function of x

Hebu\( f(x)=2x^{3/2}\). Tumia urefu wa arc wa grafu ya\( f(x)\) zaidi ya muda\( [0,1]\). Pindua jibu kwa maeneo matatu ya decimal.

Suluhisho

Tuna\( f′(x)=3x^{1/2},\) hivyo\( [f′(x)]^2=9x.\) Kisha, urefu wa arc ni

\[\begin{align*} \text{Arc Length} &=∫^b_a\sqrt{1+[f′(x)]^2}dx \nonumber \\[4pt] &= ∫^1_0\sqrt{1+9x}dx. \nonumber \end{align*}\]

Mbadala\( u=1+9x.\) Kisha,\( du=9dx.\) wakati\( x=0\), basi\( u=1\), na wakati\( x=1\), basi\( u=10\). Hivyo,

\[ \begin{align*} \text{Arc Length} &=∫^1_0\sqrt{1+9x}dx \\[4pt] =\dfrac{1}{9}∫^1_0\sqrt{1+9x}9dx \\[4pt] &= \dfrac{1}{9}∫^{10}_1\sqrt{u}du \\[4pt] &=\dfrac{1}{9}⋅\dfrac{2}{3}u^{3/2}∣^{10}_1 =\dfrac{2}{27}[10\sqrt{10}−1] \\[4pt] &≈2.268units. \end{align*}\]

Zoezi\(\PageIndex{1}\)

Hebu\(f(x)=(4/3)x^{3/2}\). Tumia urefu wa arc wa grafu ya\( f(x)\) zaidi ya muda\( [0,1]\). Pindua jibu kwa maeneo matatu ya decimal.

Kidokezo: Tumia mchakato kutoka kwa mfano uliopita. Usisahau kubadilisha mipaka ya ushirikiano.

Jibu: \[ \dfrac{1}{6}(5\sqrt{5}−1)≈1.697 \nonumber \]

Ingawa ni nzuri kuwa na formula ya kuhesabu urefu wa arc, theorem hii inaweza kuzalisha maneno ambayo ni vigumu kuunganisha. Tunasoma baadhi ya mbinu za ushirikiano katika Utangulizi wa Mbinu za Ushirikiano. Katika hali nyingine, tunaweza kutumia kompyuta au calculator ili takriban thamani ya muhimu.

Mfano\( \PageIndex{2}\): Using a Computer or Calculator to Determine the Arc Length of a Function of x

Hebu\( f(x)=x^2\). Tumia urefu wa arc wa grafu ya\( f(x)\) zaidi ya muda\( [1,3]\).

Suluhisho

Tuna\( f′(x)=2x,\) hivyo\( [f′(x)]^2=4x^2.\) Kisha urefu wa arc hutolewa na

\[\begin{align*} \text{Arc Length} &=∫^b_a\sqrt{1+[f′(x)]^2}\,dx \\[4pt] &=∫^3_1\sqrt{1+4x^2}\,dx. \end{align*}\]

Kutumia kompyuta ili takriban thamani ya muhimu hii, tunapata

\[ ∫^3_1\sqrt{1+4x^2}\,dx ≈ 8.26815. \nonumber \]

Zoezi\(\PageIndex{2}\)

Hebu\( f(x)=\sin x\). Tumia urefu wa arc wa grafu ya\( f(x)\) zaidi ya muda\( [0,π]\). Tumia kompyuta au calculator ili takriban thamani ya muhimu.

Kidokezo: Tumia mchakato kutoka kwa mfano uliopita.

Jibu: \[ \text{Arc Length} ≈ 3.8202 \nonumber \]

Urefu wa Arc wa Curve\(x = g(y)\)

Sisi tu kuona jinsi ya takriban urefu wa Curve na makundi line. Kama tunataka kupata urefu safu ya grafu ya kazi ya\(y\), tunaweza kurudia mchakato huo, ila sisi kuhesabu y-mhimili badala ya x-axis. Kielelezo\(\PageIndex{3}\) kinaonyesha sehemu ya mstari wa mwakilishi.

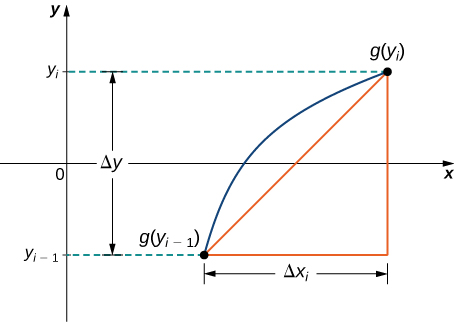
Takwimu hii ni grafu. Ni pembe upande wa kulia wa mhimili wa y kuanzia kwenye hatua g (ysubi-1). Curve inaishia katika roboduara ya kwanza kwenye hatua g (ysubi). Kati ya pointi mbili kwenye Curve ni sehemu ya mstari. Pembetatu ya kulia inaundwa na sehemu hii ya mstari kama hypotenuse, sehemu ya usawa na delta ya urefu x, na sehemu ya mstari wa wima na delta ya urefu y. — Kielelezo\(\PageIndex{3}\): Mwakilishi line sehemu juu ya muda\([y_{i−1},y_i].\)

Kisha urefu wa sehemu ya mstari ni

\[\sqrt{(Δy)^2+(Δx_i)^2}, \nonumber \]

ambayo inaweza pia kuandikwa kama

\[Δy\sqrt{1+\left(\dfrac{Δx_i}{Δy}\right)^2}. \nonumber \]

Kama sisi sasa kufuata maendeleo sawa tulifanya mapema, sisi kupata formula kwa safu urefu wa kazi\(x=g(y)\).

Urefu wa Arc kwa x = g (y)

Hebu\(g(y)\) kuwa kazi laini juu ya muda\([c,d]\). Kisha, urefu wa arc wa grafu ya\(g(y)\) kutoka hatua\((c,g(c))\) hadi hatua\((d,g(d))\) hutolewa na

\[\text{Arc Length}=∫^d_c\sqrt{1+[g′(y)]^2}dy. \nonumber \]

Mfano\(\PageIndex{3}\): Calculating the Arc Length of a Function of \(y\)

Hebu\(g(y)=3y^3.\) Tumia urefu wa arc wa grafu ya\(g(y)\) zaidi ya muda\([1,2]\).

Suluhisho

Tuna\(g′(y)=9y^2,\) hivyo\([g′(y)]^2=81y^4.\) Kisha urefu wa arc ni

\[\begin{align*} \text{Arc Length} &=∫^d_c\sqrt{1+[g′(y)]^2}dy \\[4pt] &=∫^2_1\sqrt{1+81y^4}dy.\end{align*}\]

Kutumia kompyuta ili takriban thamani ya muhimu hii, tunapata

\[ ∫^2_1\sqrt{1+81y^4}dy≈21.0277.\nonumber \]

Zoezi\(\PageIndex{3}\)

Hebu\(g(y)=1/y\). Tumia urefu wa arc wa grafu ya\(g(y)\) zaidi ya muda\([1,4]\). Tumia kompyuta au calculator ili takriban thamani ya muhimu.

Kidokezo: Tumia mchakato kutoka kwa mfano uliopita.

Jibu: \[\text{Arc Length} =3.15018 \nonumber \]

Eneo la Uso wa Mapinduzi

Dhana tulizotumia kupata urefu wa arc wa curve zinaweza kupanuliwa ili kupata eneo la uso wa mapinduzi. Eneo la uso ni eneo la jumla la safu ya nje ya kitu. Kwa vitu kama vile cubes au matofali, eneo la uso wa kitu ni jumla ya maeneo ya nyuso zake zote. Kwa nyuso za mviringo, hali hiyo ni ngumu zaidi. Hebu\(f(x)\) kuwa kazi isiyo ya negative laini juu ya muda\([a,b]\). Tunataka kupata eneo la uso wa mapinduzi lililoundwa na kuzunguka grafu ya\(y=f(x)\) karibu\(x\) -axis kama inavyoonekana katika takwimu zifuatazo.

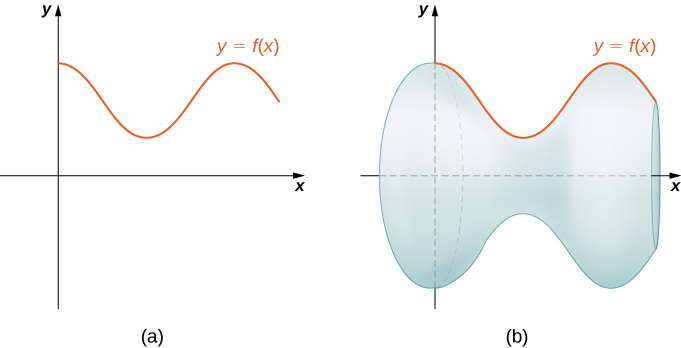
Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ni safu katika roboduara ya kwanza inayoanza kwenye mhimili wa y. Curve ni y=f (x). Grafu ya pili inaitwa “b” na ina safu sawa y=f (x). Pia kuna uso imara uliofanywa na kupokezana pembe kuhusu mhimili wa x. — Kielelezo\(\PageIndex{4}\): (a) Curve anayewakilisha kazi\(f(x)\). (b) uso wa mapinduzi sumu kwa yanazunguka graph ya\(f(x)\) karibu\(x-axis\).

Kama tulivyofanya mara nyingi kabla, tutaenda kugawanya muda\([a,b]\) na takriban eneo la uso kwa kuhesabu eneo la uso wa maumbo rahisi. Tunaanza kwa kutumia makundi ya mstari ili takriban safu, kama tulivyofanya mapema katika sehemu hii. Kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) kuwa sehemu ya kawaida ya\([a,b]\). Kisha, kwa ajili ya\(i=1,2,…,n,\) kujenga sehemu line kutoka hatua\((x_{i−1},f(x_{i−1}))\) kwa uhakika\((x_i,f(x_i))\). Sasa, zinahusu makundi haya line kuzunguka\(x\) -mhimili kuzalisha makadirio ya uso wa mapinduzi kama inavyoonekana katika takwimu zifuatazo.

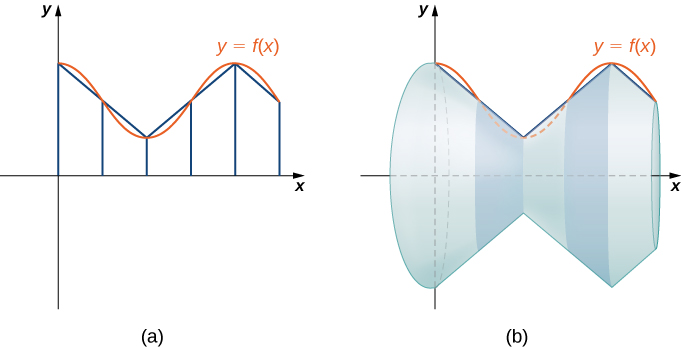
Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ni safu katika roboduara ya kwanza inayoanza kwenye mhimili wa y. Curve ni y=f (x). Eneo chini ya pembe juu ya mhimili wa x-imegawanywa katika mikoa yenye mistari ya wima. Grafu ya pili inaitwa “b” na ina safu sawa y=f (x). Pia kuna uso imara uliofanywa na kupokezana pembe kuhusu mhimili wa x. — Kielelezo\(\PageIndex{5}\): (a)\(f(x)\) Inakadiriwa na makundi ya mstari. (b) uso wa mapinduzi sumu kwa yanazunguka makundi line karibu\(x-axis\).

Kumbuka kwamba wakati kila sehemu line ni revolved kuzunguka mhimili, inazalisha bendi. Bendi hizi ni kweli vipande vya mbegu (fikiria koni ya ice cream na mwisho wa pointy kukatwa). Kipande cha koni kama hiki kinaitwa frustum ya koni.

Ili kupata eneo la uso wa bendi, tunahitaji kupata eneo la uso\(S\), la frustum (eneo la uso wa nje wa frustum, bila kujumuisha maeneo ya nyuso za juu au chini). Hebu\(r_1\) na\(r_2\) uwe radii ya mwisho wa mwisho na mwisho mwembamba wa frustum, kwa mtiririko huo, na\(l\) uwe urefu wa slant wa frustum kama inavyoonekana katika takwimu ifuatayo.

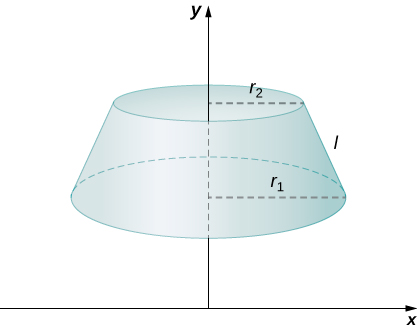
Takwimu hii ni grafu. Ni frustum ya koni juu ya x-axis na y-axis katikati. Radi ya chini ya frustum ni rsub1 na radius ya juu ni rsub2. Urefu wa upande umeandikwa “l”. — Kielelezo\(\PageIndex{6}\): Frustum ya koni inaweza takriban sehemu ndogo ya eneo la uso.

Tunajua eneo la uso wa koni linatolewa na

\[\text{Lateral Surface Area } =πrs, \nonumber \]

\(r\)wapi radius ya msingi wa koni na\(s\) ni urefu wa slant (Kielelezo\(\PageIndex{7}\)).

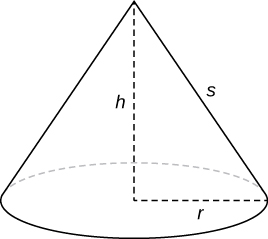
Takwimu hii ni koni. Koni ina radius r, urefu h, na urefu wa upande s. — Kielelezo\(\PageIndex{7}\): Eneo la uso wa koni linatolewa na\(πrs\).

Kwa kuwa frustum inaweza kuchukuliwa kama kipande cha koni, eneo la uso wa frustum lateral hutolewa na eneo la uso wa koni nzima chini ya eneo la uso wa koni ndogo (ncha ya pointy) iliyokatwa (Kielelezo\(\PageIndex{8}\)).

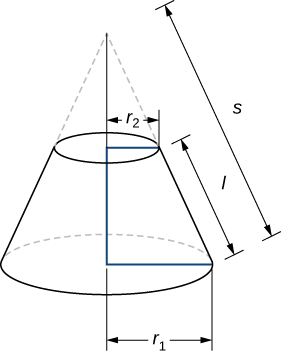
Takwimu hii ni grafu. Ni frustum ya koni. Radi ya chini ya frustum ni rsub1 na radius ya juu ni rsub2. Urefu wa upande umeandikwa “l”. Pia kuna juu ya koni na mistari iliyovunjika juu ya frustum. Ina urefu wa upande s. — Kielelezo\(\PageIndex{8}\): Kuhesabu eneo la uso wa ndani wa frustum ya koni.

Sehemu ya msalaba wa koni ndogo na koni kubwa ni pembetatu sawa, kwa hiyo tunaona hiyo

\[ \dfrac{r_2}{r_1}=\dfrac{s−l}{s} \nonumber \]

Kutatua kwa\(s\), tunapata =s-ls

\[\begin{align*} \dfrac{r_2}{r_1} &=\dfrac{s−l}{s} \\ r_2s &=r_1(s−l) \\ r_2s &=r_1s−r_1l \\ r_1l &=r_1s−r_2s \\ r_1l &=(r_1−r_2)s \\ \dfrac{r_1l}{r_1−r_2} =s \end{align*}\]

Kisha eneo la uso lateral (SA) la frustum ni

\[\begin{align*} S &= \text{(Lateral SA of large cone)}− \text{(Lateral SA of small cone)} \\[4pt] &=πr_1s−πr_2(s−l) \\[4pt] &=πr_1(\dfrac{r_1l}{r_1−r_2})−πr_2(\dfrac{r_1l}{r_1−r_2−l}) \\[4pt] &=\dfrac{πr^2_1l}{r^1−r^2}−\dfrac{πr_1r_2l}{r_1−r_2}+πr_2l \\[4pt] &=\dfrac{πr^2_1l}{r_1−r_2}−\dfrac{πr_1r2_l}{r_1−r_2}+\dfrac{πr_2l(r_1−r_2)}{r_1−r_2} \\[4pt] &=\dfrac{πr^2_1}{lr_1−r_2}−\dfrac{πr_1r_2l}{r_1−r_2} + \dfrac{πr_1r_2l}{r_1−r_2}−\dfrac{πr^2_2l}{r_1−r_3} \\[4pt] &=\dfrac{π(r^2_1−r^2_2)l}{r_1−r_2}=\dfrac{π(r_1−r+2)(r1+r2)l}{r_1−r_2} \\[4pt] &= π(r_1+r_2)l. \label{eq20} \end{align*} \]

Hebu sasa kutumia formula hii kwa mahesabu ya eneo la uso wa kila moja ya bendi sumu na yanazunguka makundi line karibu\(x-axis\). Bendi ya mwakilishi inavyoonekana katika takwimu zifuatazo.

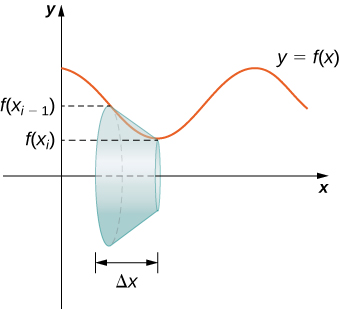
Takwimu hii ina graphics mbili. Ya kwanza ni safu katika quadrant ya kwanza. Karibu na x-axis ni frustum ya koni. Makali ya frustum ni kinyume na curve. Makali huanza saa f (xsubi-1) na kuishia katika f (xsubi). Picha ya pili ni safu sawa na frustum sawa. urefu wa frustum ni delta x na curve inaitwa y=f (x). — Kielelezo\(\PageIndex{9}\): bendi mwakilishi kutumika kwa ajili ya kuamua eneo la uso.

Kumbuka kwamba urefu wa slant wa frustum hii ni urefu tu wa sehemu ya mstari inayotumiwa kuzalisha. Hivyo, kwa kutumia formula eneo la uso, tuna

\[\begin{align*} S &=π(r_1+r_2)l \\ &=π(f(x_{i−1})+f(x_i))\sqrt{Δx^2+(Δyi)^2} \\ &=π(f(x_{i−1})+f(x_i))Δx\sqrt{1+(\dfrac{Δy_i}{Δx})^2} \end{align*}\]

Sasa, kama tulivyofanya katika maendeleo ya formula ya urefu wa arc, tunatumia Theorem ya Theorem ya Theorem ya\(x^∗_i∈[x_{i−1},x_i]\) Maana kuchagua vile kwamba\(f′(x^∗_i)=(Δy_i)/Δx.\) Hii inatupa

\[S=π(f(x_{i−1})+f(x_i))Δx\sqrt{1+(f′(x^∗_i))^2} \nonumber \]

Zaidi ya hayo, tangu\(f(x)\) ni kuendelea, na Theorem ya Thamani ya Kati, kuna hatua\(x^{**}_i∈[x_{i−1},x[i]\) kama kwamba\ (f (x^ {**} _i) =( 1/2) [f (xi-1) +f (xi)],

hivyo tunapata

\[S=2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2}.\nonumber \]

Kisha eneo la uso takriban la uso mzima wa mapinduzi hutolewa na

\[\text{Surface Area} ≈\sum_{i=1}^n2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2}.\nonumber \]

Hii karibu inaonekana kama jumla Riemann, ila tuna kazi tathmini katika pointi mbili tofauti,\(x^∗_i\) na\(x^{**}_{i}\), zaidi ya muda\([x_{i−1},x_i]\). Ingawa hatuwezi kuchunguza maelezo hapa, zinageuka kuwa kwa sababu\(f(x)\) ni laini, kama sisi basi n\(→∞\), kikomo kazi sawa na jumla Riemann hata kwa pointi mbili tofauti tathmini. Hii inafanya hisia intuitively. Wote\(x^∗_i\) na x^ {**} _i\) ni katika kipindi\([x_{i−1},x_i]\), hivyo ni mantiki kwamba kama\(n→∞\), wote\(x^∗_i\) na\(x^{**}_i\) mbinu\(x\) Wale ambao ni nia ya maelezo wanapaswa kushauriana juu calculus maandishi.

Kuchukua kikomo kama\(n→∞,\) sisi kupata

\[ \begin{align*} \text{Surface Area} &=\lim_{n→∞}\sum_{i=1}n^2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2} \\[4pt] &=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2}) \end{align*}\]

Kama na urefu wa arc, tunaweza kufanya maendeleo sawa kwa ajili ya kazi ya\(y\) kupata formula kwa eneo la uso wa nyuso za mapinduzi kuhusu\(y-axis\). Matokeo haya ni muhtasari katika theorem zifuatazo.

Eneo la uso wa Mapinduzi

Hebu\(f(x)\) kuwa kazi isiyo ya negative laini juu ya muda\([a,b]\). Kisha, eneo la uso wa mapinduzi lililoundwa na kuzunguka grafu ya\(f(x)\) karibu na x-axis hutolewa na

\[\text{Surface Area}=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2})dx \nonumber \]

Vile vile, hebu\(g(y)\) iwe kazi isiyo ya negative laini juu ya muda\([c,d]\). Kisha, eneo la uso wa mapinduzi lililoundwa na\(g(y)\) zinazozunguka grafu ya karibu\(y-axis\) hutolewa na

\[\text{Surface Area}=∫^d_c(2πg(y)\sqrt{1+(g′(y))^2}dy \nonumber \]

Mfano\(\PageIndex{4}\): Calculating the Surface Area of a Surface of Revolution 1.

Hebu\(f(x)=\sqrt{x}\) juu ya muda\([1,4]\). Pata eneo la uso wa uso unaozalishwa na kuzunguka grafu ya\(f(x)\) karibu na\(x\) -axis. Pindua jibu kwa maeneo matatu ya decimal.

Suluhisho

Grafu ya\(f(x)\) na uso wa mzunguko huonyeshwa kwenye Kielelezo\(\PageIndex{10}\).

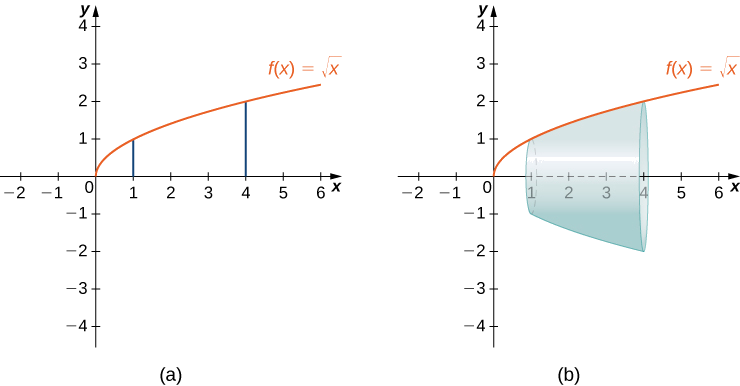
Takwimu hii ina grafu mbili. Ya kwanza ni safu f (x) =squareroot (x). Curve inaongezeka na huanza kwa asili. Pia kwenye grafu ni mistari ya wima x=1 na x=4. Grafu ya pili ni kazi sawa na grafu ya kwanza. Eneo kati ya f (x) na x-axis, lililofungwa na x=1 na x=4 limezungushwa karibu na x-axis ili kuunda uso. — Kielelezo\(\PageIndex{10}\): (a) grafu ya\(f(x)\). (b) Upeo wa mapinduzi.

Tuna\(f(x)=\sqrt{x}\). Kisha,\(f′(x)=1/(2\sqrt{x})\) na\((f′(x))^2=1/(4x).\) kisha,

\[\begin{align*} \text{Surface Area} &=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2}dx \\[4pt] &=∫^4_1(\sqrt{2π\sqrt{x}1+\dfrac{1}{4x}})dx \\[4pt] &=∫^4_1(2π\sqrt{x+14}dx. \end{align*}\]

Basi\(u=x+1/4.\) basi,\(du=dx\). Wakati\(x=1, u=5/4\), na wakati\(x=4, u=17/4.\) Hii inatupa

\[\begin{align*} ∫^1_0(2π\sqrt{x+\dfrac{1}{4}})dx &= ∫^{17/4}_{5/4}2π\sqrt{u}du \\[4pt] &= 2π\left[\dfrac{2}{3}u^{3/2}\right]∣^{17/4}_{5/4} \\[4pt] &=\dfrac{π}{6}[17\sqrt{17}−5\sqrt{5}]≈30.846 \end{align*}\]

Zoezi\(\PageIndex{4}\)

Hebu\( f(x)=\sqrt{1−x}\) juu ya muda\( [0,1/2]\). Pata eneo la uso wa uso unaozalishwa na kuzunguka grafu ya\( f(x)\) karibu na\(x\) -axis. Pindua jibu kwa maeneo matatu ya decimal.

Kidokezo: Tumia mchakato kutoka kwa mfano uliopita.

Jibu: \[ \dfrac{π}{6}(5\sqrt{5}−3\sqrt{3})≈3.133 \nonumber \]

Mfano\( \PageIndex{5}\): Calculating the Surface Area of a Surface of Revolution 2

Hebu\( f(x)=y=\dfrac[3]{3x}\). Fikiria sehemu ya Curve ambapo\( 0≤y≤2\). Pata eneo la uso wa uso unaozalishwa na kuzunguka grafu ya\( f(x)\) karibu na\( y\) -axis.

Suluhisho

Kumbuka kwamba sisi ni yanazunguka Curve kuzunguka\( y\) -axis, na muda ni katika suala la\( y\), hivyo tunataka kuandika upya kazi kama kazi ya\( y\). Tunapata\( x=g(y)=(1/3)y^3\). Grafu ya\( g(y)\) na uso wa mzunguko huonyeshwa kwenye takwimu ifuatayo.

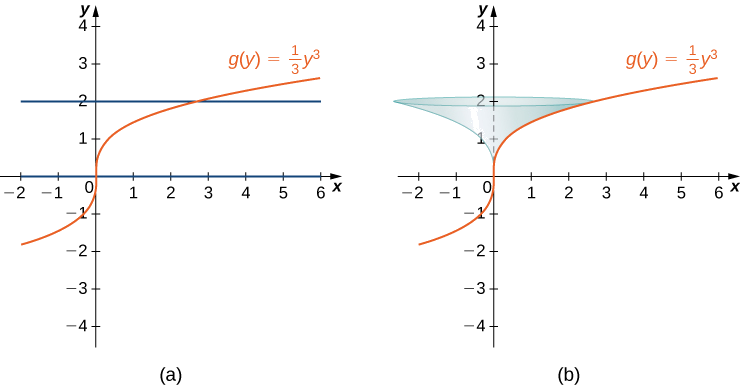
Takwimu hii ina grafu mbili. Ya kwanza ni Curve g (y) =1/3y ^ 3. Curve inaongezeka na huanza kwa asili. Pia kwenye grafu ni mistari ya usawa y=0 na y=2. Grafu ya pili ni kazi sawa na grafu ya kwanza. Eneo kati ya g (y) na y axis, lililofungwa na y=0 na y=2 limezungushwa karibu na mhimili y ili kuunda uso. — Kielelezo\(\PageIndex{11}\): (a) grafu ya\( g(y)\). (b) Upeo wa mapinduzi.

tuna\( g(y)=(1/3)y^3\), hivyo\( g′(y)=y^2\) na\( (g′(y))^2=y^4\). Kisha

\[\begin{align*} \text{Surface Area} &=∫^d_c(2πg(y)\sqrt{1+(g′(y))^2})dy \\[4pt] &=∫^2_0(2π(\dfrac{1}{3}y^3)\sqrt{1+y^4})dy \\[4pt] &=\dfrac{2π}{3}∫^2_0(y^3\sqrt{1+y^4})dy. \end{align*}\]

Basi\( u=y^4+1.\) basi\( du=4y^3dy\). Lini\( y=0, u=1\), na lini\( y=2, u=17.\) Kisha

\[\begin{align*} \dfrac{2π}{3}∫^2_0(y^3\sqrt{1+y^4})dy &=\dfrac{2π}{3}∫^{17}_1\dfrac{1}{4}\sqrt{u}du \\[4pt] &=\dfrac{π}{6}[\dfrac{2}{3}u^{3/2}]∣^{17}_1=\dfrac{π}{9}[(17)^{3/2}−1]≈24.118. \end{align*}\]

Zoezi\(\PageIndex{5}\)

Hebu\( g(y)=\sqrt{9−y^2}\) juu ya muda\( y∈[0,2]\). Pata eneo la uso wa uso unaozalishwa na kuzunguka grafu ya\( g(y)\) karibu na\( y\) -axis.

Kidokezo: Tumia mchakato kutoka kwa mfano uliopita.

Jibu: \( 12π\)

Dhana muhimu

Urefu wa arc wa curve unaweza kuhesabiwa kwa kutumia muhimu ya uhakika.
Urefu wa arc ni wa kwanza ulipangwa kwa kutumia makundi ya mstari, ambayo huzalisha jumla ya Riemann. Kuchukua kikomo basi inatupa uhakika muhimu formula. Mchakato huo unaweza kutumika kwa kazi za\( y\).
Dhana zilizotumiwa kuhesabu urefu wa arc zinaweza kuzalishwa ili kupata eneo la uso wa mapinduzi.
Vipengele vinavyotokana na urefu wa arc na fomu za eneo la uso mara nyingi ni vigumu kutathmini. Inaweza kuwa muhimu kutumia kompyuta au calculator ili takriban maadili ya integrals.

Mlinganyo muhimu

Arc Urefu wa Kazi ya x

Urefu wa Arc\( =∫^b_a\sqrt{1+[f′(x)]^2}dx\)

Urefu wa Arc wa Kazi ya y

Urefu wa Arc\( =∫^d_c\sqrt{1+[g′(y)]^2}dy\)

Eneo la Uso wa Kazi ya x

Eneo la uso\( =∫^b_a(2πf(x)\sqrt{1+(f′(x))^2})dx\)

faharasa

urefu wa arc: urefu wa arc wa curve unaweza kufikiriwa kama umbali mtu angeweza kusafiri kando ya njia ya curve

msuguano: sehemu ya koni; frustum hujengwa kwa kukata koni na ndege inayofanana na msingi

eneo la uso: eneo la uso wa imara ni eneo la jumla la safu ya nje ya kitu; kwa vitu kama vile cubes au matofali, eneo la uso wa kitu ni jumla ya maeneo ya nyuso zake zote